4(2)受弯构件的正截面受弯承载力-计算原理-单筋矩形截面(精)

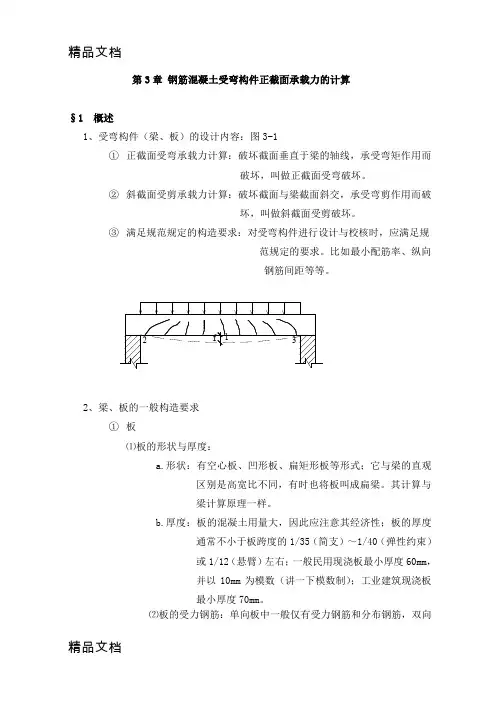
第3章钢筋混凝土受弯构件正截面承载力的计算§1概述1、受弯构件（梁、板）的设计内容：图3-1①正截面受弯承载力计算：破坏截面垂直于梁的轴线，承受弯矩作用而破坏，叫做正截面受弯破坏。

②斜截面受剪承载力计算：破坏截面与梁截面斜交，承受弯剪作用而破坏，叫做斜截面受剪破坏。

③满足规范规定的构造要求：对受弯构件进行设计与校核时，应满足规范规定的要求。

比如最小配筋率、纵向2①板⑴板的形状与厚度：a.形状：有空心板、凹形板、扁矩形板等形式；它与梁的直观区别是高宽比不同，有时也将板叫成扁梁。

其计算与梁计算原理一样。

b.厚度：板的混凝土用量大，因此应注意其经济性；板的厚度通常不小于板跨度的1/35（简支）～1/40（弹性约束）或1/12（悬臂）左右；一般民用现浇板最小厚度60mm，并以10mm为模数（讲一下模数制）；工业建筑现浇板最小厚度70mm。

⑵板的受力钢筋：单向板中一般仅有受力钢筋和分布钢筋，双向板中两个方向均为受力钢筋。

一般情况下互相垂直的两个方向钢筋应绑扎或焊接形成钢筋网。

当采用绑扎钢筋配筋时，其受力钢筋的间距：当板厚度h≤150mm时，不应大于200mm，当板厚度h﹥150mm时，不应大于1.5h，且不应大于250mm。

板中受力筋间距一般不小于70mm，由板中伸入支座的下部钢筋，其间距不应大于400mm，其截面面积不应小于跨中受力钢筋截面面积的1/3，其锚固长度l as不应小于5d。

板中弯起钢筋的弯起角不宜小于30°。

板的受力钢筋直径一般用6、8、10mm。

对于嵌固在砖墙内的现浇板，在板的上部应配置构造钢筋，并应符合下列规定：a. 钢筋间距不应大于200mm，直径不宜小于８mm（包括弯起钢筋在内），其伸出墙边的长度不应小于l1/7(l1为单向板的跨度或双向板的短边跨度)。

b. 对两边均嵌固在墙内的板角部分，应双向配置上部构造钢筋，其伸出墙边的长度不应小于l1/4。

c. 沿受力方向配置的上部构造钢筋，直径不宜小于6mm，且单位长度内的总截面面积不应小于跨中受力钢筋截面面积的1/3。

根据公式
a1 f c bx f y As
直接求得所需的钢筋面积。
并应满足As ≥ minbh；
若≥出现As<minbh时，则应按minbh配筋。
计算步骤4
选择钢筋直径并进行截面布置，得
到实际配筋面积As、as和h0。
截面设计
控制截面
在等截面受弯构件中，指弯矩组合设
计值最大的截面；在变截面受弯构件中，
构件种类
梁
板
纵向受力钢
筋层数
1层
2层
1层
混凝土强度等级
≤ 25
45mm
70mm
25mm
≥ 30
40mm
65mm
20mm
计算步骤2
根据公式
x
M a1 f c bx( h0 )
2
解一元二次方程求得截面受压区高度x，并满足
x b h0
否则应加大截面，或提高fc ，或改用双筋梁。
计算步骤3
单筋矩形截面受弯构件截面复核
（建筑规范）
截面复核：是指已知截面尺寸、混凝土和钢筋
强度级别以及钢筋在截面上的布置，要求计算截面
的承载力Mu或复核控制截面承受某个弯矩计算值M是
否安全。
截面尺寸
已知条件
材料强度级别
钢筋在截面上的布置
钢筋布置
复核内容
配筋率
截面的承载力Mu
复核步骤1
检查钢筋布置是否符合
M u f cd bh02 b 1 0.5 b
当由上式求得的Mu<M时，可采取提高混凝土
级别、修改截面尺寸，或改为双筋截面等措施；
复核步骤五
当x≤ξbh0时，由公式
x

M u f cd bxM u f sd As h0

h0—有效高度。 1.最大配筋率及界限相对受压区高度
r As f y As a1 fcbx x a1 fc
bh0 bh0 f y bh0 f y h0 f y
令
x
h0
则
r
a1 fc
fy
令b为 = r max时的相对受压区高度，即
rmax
b
a1
f
fc
y
= r max时的破坏形态为受压区边缘混凝土达到极限压
c fc e0 e ecu
n
2
1 60
(
fcu,k
50)
2.0
各系数查表4-3
e0 0.002 0.5( fcu,k 50)105 0.002
ecu 0.0033 0.5( fcu,k 50)105 0.0033
4.钢筋应力—应变关系的假定（本构关系）
Ese e e y fy e ey
4.3钢筋混凝土受弯构件正截面试验研究
一、受弯构件正截面破坏过程
受弯构件正截面破坏分为三个阶段 • 第一阶段：裂缝开裂前 • 第二阶段：从开裂到钢筋屈服 • 第三阶段：从钢筋屈服到梁破坏
（1）第I阶段
当荷载比较小时，混凝土基本处 于弹性阶段，截面上应力分布为三 角形，荷载-挠度曲线或弯矩-曲率 曲线基本接近直线。截面抗弯刚度 较大，挠度和截面曲率很小，钢筋 的应力也很小，且都于弯矩近似成 正比。
My
Mu
Failure”，破坏前
可吸收较大的应变
能。
0
f
2．超筋梁(Over reinforced)破坏
钢筋配置过多，将发生这种破坏。 破坏特征：破坏时钢筋没有达到屈服强度，破坏是由 于压区混凝土被压碎引起，没有明显预兆，为脆性破 坏。

未裂阶段 没有裂缝，挠度很小 大致成直线 直线
前期为直线，后期为有 上升段的曲线，应力峰 值不在受拉区边缘 σs≤20～30kN/mm2 Ia阶段用于抗裂验算
带裂缝工作阶段 有裂缝，挠度还不 明显
曲线
受压区高度减小， 混凝土压应力图形 为上升段的曲线， 应力峰值在受压区 边缘
大部分退出工作
20～ 30kN/mm2<σs<fy0 用于裂缝宽度及变 形验算
4.3.3 正截面受弯的三种破坏形态
适筋破坏
配 筋 超筋破坏 率 ρ
少筋破坏
适筋破坏形态
min
h h0
b
最

筋
率
率
特点：纵向受拉钢筋先屈服，受压区混凝土 随后压碎。
梁完全破坏以前，钢筋要经历较大的塑性变 形，随后引起裂缝急剧开展和梁挠度的激增， 带有明显的破坏预兆，属于延性破坏类型。
M0
h0=h-as
纵向受拉钢筋配筋率为
As (%)
bh0
纵向受拉钢筋的配筋百分率ρ在一定程度上标志了正截面上纵向受拉钢 筋与混凝土之间的面积比率，它是对梁的受力性能有很大影响的一个 重要指标。
混凝土保护层
混凝土保护层厚度c－纵向受力钢筋的外表面到截面边缘 的垂直距离。
保护层厚度的作用：
a. 保护纵向钢筋不被锈蚀；
梁中纵向受力钢筋宜采用HRB400级或RRB400级(Ⅲ级)和HRB335级 (Ⅱ级)，常用直径为12mm、14mm、16mm、18mm、20mm、22mm 和25mm。根数最好不少于3(或4)根。设计中若采用两种不同直径的钢 筋，其直径相差至少2mm,也不宜超过6mm。
梁的箍筋宜采用HPB235级(Ⅰ级)、HRB335(Ⅱ级)和HRB400(Ⅲ级钢 筋)级的钢筋，常用直径是6mm、8mm和10mm。

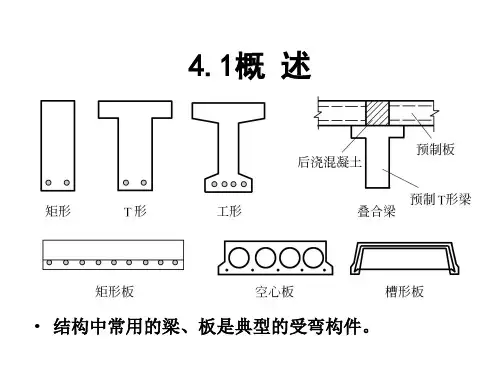
单筋矩形截面受弯构件正截面承载力计算单筋矩形截面受弯构件是指具有一个纵向钢筋（单筋）和一个矩形截面的构件。

在受弯时，矩形截面受到压力，而钢筋受到拉力，通过计算正截面承载力可以确定该构件的安全性能。

下面将介绍单筋矩形截面受弯构件正截面承载力的计算方法。

首先，计算正截面的受压区高度h和内力矩M。

假设构件受弯时的截面高度为h，宽度为b，截面厚度为d。

根据等截面原则，构件的正截面宽度和截面高度相等，即b=h。

构件的弯矩M由下式计算得出：M=Rd·Z，其中Rd为设计弯矩，Z为正截面抵抗矩。

然后，计算正截面抵抗矩Z。

在单筋矩形截面中，正截面抵抗矩由钢筋和混凝土组成。

钢筋的抵抗矩可由以下公式计算得出：Zs=As·fy·(h-d/2)，其中As为钢筋截面面积，fy为钢筋的抗拉强度。

混凝土的抵抗矩可由以下公式计算得出：Zc=0.85·fck·(b·h-(As+Asc)·(h/2-d/2))，其中fck为混凝土的抗压强度，Asc为纵向钢筋表面积。

正截面的抵抗矩由钢筋的抵抗矩和混凝土的抵抗矩之和得出：Z=Zs+Zc。

接下来，计算正截面的承载力。

正截面受弯构件的承载力由以下条件中的最不利情况决定：1.混凝土达到极限压应力或者钢筋达到屈服应力；2. 混凝土达到达到破坏应变时，即混凝土压应力达到0.45fck或者钢筋达到屈服应变。

计算混凝土达到极限压应力的情况下的承载力，可以得到下式：Nc=0.85·fcd0·A+(Rd-Zs)/Rd·fctd0·A，其中fcd0为混凝土的设计强度，fctd0为混凝土的设计抗拉强度，A为截面面积。

计算钢筋达到屈服应力的情况下的承载力，可以得到下式：Ns=(Zs/0.9zτs)·fsd，其中z为混凝土的截面中和高度，τs为混凝土的应力分布系数，fsd为钢筋的设计抗拉强度。

综合两种情况，正截面受弯构件的正截面承载力Fc为较小值：Fc=min{Nc,Ns}。

图形在第I阶段前期是直线，后期是曲线。 3）弯矩与截面曲率基本上是直线关系。 #Ia阶段可作为受弯构件抗裂度的计算依据。
*第II阶段：混凝土开裂后至钢筋屈服前的裂缝阶段
M0=Mcr0时，在纯弯段抗拉能力最薄弱的某一截面处， 当受拉区边缘纤维的拉应变值到达混凝土极限拉应变实验
值εtu0时，将首先出现第一条裂缝，一旦开裂，梁即由第
3
结构和构件要满足承载能力极限状态和正常使用极 限状态的要求。梁、板正截面受弯承载力计算就是从满 足承载能力极限状态出发的，即要求满足
M≤Mu
(4—1)
式中的M是受弯构件正截面的弯矩设计值，它是由结构 上的作用所产生的内力设计值；Mu是受弯构件正截面受
弯承载力的设计值，它是由正截面上材料所产生的抗力。
侧面构造钢筋—用以增强钢筋骨架的刚性，提高梁的抗 扭能力，并承受因温度变化和混凝土收缩所产生的拉应力 ，抑制梁侧裂缝开展。
2）梁纵向受力钢筋应采用HRB400、HRB500、HRBF400、
HRBF500钢筋 ，常用直径为12mm、14mm、16mm、18mm、
20mm、22mm和25mm。根数最好不少于3(或4)根。
4
因此，进行钢筋混凝土构件设计时，除了计算满足以外， 还必须满足有关构造要求。
4.1.1截面形状与尺寸
1.截面形状：梁、板常用矩形、T形、I字形、槽形、空心 板和倒L形梁等对称和不对称截面。
(a)
(b)
(c)
(d)
(e)
(f)
(g)
5
2.截面尺寸 确定原则：A.考虑模板模数；B.尽量统一、方便施工。
1000mm等尺寸。800mm以下的级差为50mm，以上的为l00mm。 （3）现浇板的宽度一般较大，设计时可取单位宽度

◆判别条件：f y As 1 fcb'f h'f
第一类T形截面
满足：
0M 1 fcb'f h'f h0 h'f 2 否则为第二类截面
混凝土结构设计原理
第4章
■第一类T形截面的计算公式及适用条件
图4.13 第一类T形截面计算简图
◆计算公式： 1 fcbf x f y As
0M
1
f cbf x(h0
由式（4-27）可得：
x h0
h02
M 2
fyAs(h0
1 fcb
as)
As
fyAs 1 fcbx
fy
…4－34 …4－35
混凝土结构设计原理 情形2：已知条件
第4章
M1
0M
f
' y
As'
h0
as'
x h0
h02
M1
0.51 fcb
x h0 b N
Y
x 2as'
按 A未s' 知，重新计算 和As' As
x) 2
◆适用条件： 1.防止超筋破坏： x bh0 2.防止少筋破坏 ： As minbh
按 bf h的单筋
矩形截面计算
混凝土结构设计原理
第4章
■第二类T形截面的计算公式及适用条件
图4.14 第二类T形截面计算简图
◆计算公式： 1 fcbx 1 fc (bf b)hf fy As
0M
② 由式（4-27）求 Mu
Mu
fyAs(h0 as) 1 fcbx(h0
x) 2
…4－37
③ 验算： Mu M ?
混凝土结构设计原理

求：截面配筋As
2.已知：矩形截面钢筋混凝土简支梁，计算跨度为6000mm， as=35mm, 作用均布荷载25 kN/m，混凝土强度等级C20，钢筋HRB335级。 （ fc =9.6 N/mm2 ， ft =1.1 N/mm2 ， fy =300 N/mm2 ）
试设计此梁
3.已知：矩形截面梁尺寸b＝200mm、h＝450mm，as=35mm。混凝土 强度等级C70，钢筋HRB335级，实配4根20mm的钢筋。 （ fc =31.8 N/mm2 ， ft =2.14 N/mm2 ， fy =300 N/mm2 ）
b
max
b
1 fc
fy
受弯构件正截面承载力计算
最小配筋率ρmin
最小配筋率规定了少筋和适筋的界限
m in
As bh
0.45
ft fy
且同时不应小于0.2%
受弯构件正截面承载力计算
造价
总造价
混凝土
钢
经济配筋率
经济配筋率 板：0.4~0.8%
矩形梁：0.6~1.5% T形梁：0.9~1.8%
受弯构件正截面承载力计算
小相等； 2. 等效矩形应力图形与实际抛物线应力图形的形心位置相同，即合
力作用点不变。
受弯构件正截面承载力计算
表 5.1 混凝土受压区等效矩形应力图系数
≤C50 C55
C60
C65
C
0.8
0.99 0.98 0.97 0.96 0.95 0.94 0.79 0.78 0.77 0.76 0.73 0.74
钢筋与混凝土的材料强度比，是反映构件中两种材料配比的本质参数。
基本方程改为：
N 0, M 0,
1 fcb h0 s As M u 1 fcbh02 (1 0.5 )

受压混凝土的应力－应变关系
计算原则
2）等效矩形应力图
简化原则：受压区混凝土的合力大小不变；受压区混凝土的合力作用点不变。
等效矩形应力图形的混凝土受压区高度 x 1xn ，等效矩形应力图形的应力值 为 1 fc， 1、1 的值见下表。
表 1、1 值
混凝土强 度等级
≤C50
C55
C60
C65
C70
C75
（2）求跨中截面的最大弯矩设计值。
因仅有一个可变荷载，故弯矩设计值应有取下列两者中的较大值：
M 1 1.2g 1.4q l 2
8
1 1.2 5 1.4 10 5.02 62.5
8
M 1 1.35g 1.4 0.7q l 2
8
1 1.35 5 1.4 0.7 10 5.02 51.7
需要加固、补强
计算原则
1）基本假定
01 平截面假定。
02
钢筋的应力 s 等于钢筋应变 s 与其弹性模量 Es 的乘积，但不得大
于其强度设计值 fy，即
s sEs fv
03 不考虑截面受拉区混凝土的抗拉强度。
计算原则
04
受压混凝土采用理想化的应力－应变关系，当混凝土强度等级为
C50及以下时，混凝土极限压应变 cu=0.0033。
（1）受拉钢筋为4 25，As=1964 mm2； （2）受拉钢筋为3 18，As=763 mm²。
单筋矩形截面梁计算
解 查表得：
fc 9.6N/mm2
ft 1.10N/mm2
f y 300N/mm2 c 1.0
b 0.550
c 30mm
单筋矩形截面梁计算
（1）
d
25
h0 h c 2 450 30 2 408

fsd
即：
截面应力图
截面等效应力图
fcdb x k1 fcdb xc
x 2 xc yc 2 1 k2 xc
令：x xc ，可求出 21 k2 ,
k1
21 k2
对 C50 及以下混凝土， 1.0 ， 0.8 ；C80时， 0.94
0.74 ，中间内插值。《公路桥规》直接取 1.0。
k2 xc
cu c c d c
0
式中k1、k2与混凝土的 强度等级有关，对C50 及以下混凝土，积分 可得 k1=0.797
k2=0.588
4.3 正截面受弯承载力计算原理
第4章 受弯构件的正截面受弯承载力
3.等效矩形应力图
fcd
等效原则：
合力大小C 相等
合力点位置 yc不变
fsd
4.3 正截面受弯承载力计算原理
第4章 受弯构件的正截面受弯承载力
4.适筋梁与超筋梁的界限及界限配筋率 （1）界限破坏
适筋破坏：受拉钢筋先屈服，
然后混凝土受压区边缘达到极限压
应变。
超筋破坏：受拉钢筋不屈服，
混凝土受压区边缘达到极限压应变。
界限破坏：受拉钢筋屈服的同 时混凝土受压区边缘达到极限压应
适筋、超筋、界限破坏时的截面应变
4.1 梁、板的一般构造
第4章 受弯构件的正截面受弯承载力
常用直径为8mm、10mm、12mm和14mm。 ■ 板内钢筋： 受力钢筋宜采用HPB300、HRB400和HRBF400钢筋。 常用直径为8mm、10mm、12mm和14mm。 分布钢筋宜采用HPB300、HRB335钢筋。 常用直径为6mm、8mm。 ■ 钢筋净距、保护层及有效高度 截面有效高度h0为受拉钢筋合力点至受压区边缘的距离。 h0 h as

三、混凝土保护层厚度c和截面有效高度 1．混凝土保护层厚度c 1）作用
防止钢筋锈蚀；保证混凝土对受力筋的锚固。 2）定义
构件最外层钢筋（包括箍筋、分布筋等构造筋）的 外缘至混凝土表面的最小距离c。
14
第三章 受弯构件正截面承载力计算
3）规定
①c不应小于钢筋的公称直径d或并筋的等效直径de； ②设计使用年限为50年的混凝土结构，c还应符合表3-2的规定； ③设计使用年限为100年的混凝土结构，c不应小于表3-2中数
12
第三章 受弯构件正截面承载力计算
（2）架立钢筋
1）作用
①形成钢筋骨架；
②承受混凝土收缩及温度变化产生的拉力。
2）要求
当梁上部无受压钢筋时，需配置2根；
当梁的跨度l0＜4m时，直径不宜小于8mm；
当l0＝4m～6m时，直径不应小于10mm；
当l0＞6m时，直径不宜小于12mm。
13
第三章 受弯构件正截面承载力计算
纵向受力钢筋的最小间距
间距类型 钢筋类型 最小间距
水平净距
上部钢筋
下部钢筋
30mm和1.5d
25mm和d
垂直净距（层距） 25mm和d
注 1.当梁的下部钢筋配置多于二层时，两层以上钢筋水平方向的中距应比下面两层的 中距增大一倍；
2.d为钢筋的最大直径。
10
第三章 受弯构件正截面承载力计算
③梁的配筋密集区域，当受力钢筋单根配置导致混 凝土难以浇筑密实时，可采用两根或三根一起配置 的并筋形式。
值的1.5倍。 ④当有充分依据并采取一定的有效措施时，可适当减小混凝土
保护层的厚度。
表3-2 混凝土保护层厚度的最小厚度
环境类别
一 二a 二b 三a 三b

1 /171第四章 钢筋混凝土受弯构件正截面承载力计算本章学习要点:1、掌握单筋矩形截面、双筋矩形截面和T 形截面承载力的计算方法；2、了解配筋率对受弯构件破坏特征的影响和适筋受弯构件在各阶段的受力特点；3、熟悉受弯构件正截面的构造要求。

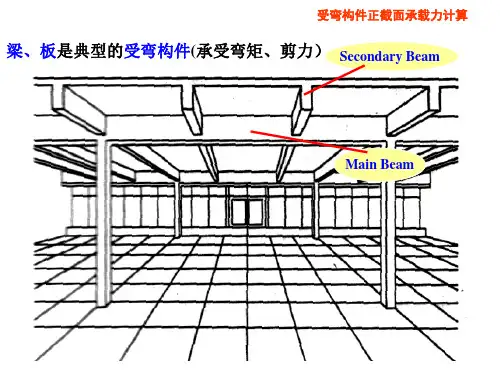
§4－1 概述一、受弯构件的定义同时受到弯矩M 和剪力V 共同作用，而轴力N 可以忽略的构件（图4—1)． 梁和板是土木工程中数量最多，使用面最广的受弯构件。

梁和板的区别：梁的截面高度一般大于其宽度，而板的截面高度则远小于其宽度。

受弯构件常用的截面形状如图4-2所示。

图4-1二、受弯构件的破坏特性正截面受弯破坏:沿弯矩最大的截面破坏,破坏截面与构件的轴线垂直。

斜截面破坏：沿剪力最大或弯矩和剪力都较大的截面破坏。

破坏截面与构件轴线斜交。

进行受弯构件设计时，要进行正截面承载力和斜截面承载力计算。

2 /172图4—3 受弯构件的破坏特性§4—2 受弯构件正截面的受力特性一、配筋率对正截面破坏性质的影响配筋率:为纵向受力钢筋截面面积A s 与截面有效面积的百分比.sA bh 式中 s A —-纵向受力钢筋截面面积。

b -—截面宽度，0h —－截面的有效高度（从受压边缘至纵向受力钢筋截面重心的距离)。

构件的破坏特征取决于配筋率、混凝土的强度等级、截面形式等诸多因素，但配筋率的影响最大。

受弯构件依配筋数量的多少通常发生如下三种破坏形式: 1、 少筋破坏当构件的配筋率低于某一定值时,构件不但承载力很低,而且只要其一开裂，裂缝就急速开展，裂缝处的拉力全部由钢筋承担,钢筋由于突然增大的应力而屈服,构件立即发生破坏。

图4—4 受弯构件正截面破坏形态2、适筋破坏当构件的配筋率不是太低也不是太高时,构件的破坏首先是受拉区纵向钢筋屈服，然后压区砼压碎。

钢筋和混凝土的强度都得到充分利用.破坏前有明显的塑性变形和裂缝预兆。

3、超筋破坏当构件的配筋率超过一定值时,构件的破坏是由于混凝土被压碎而引起的。

··
As2fy
b
(c)
43
问题: 在T形截面设计时, 怎样利用单筋矩形截面的
表格 (, , )。
M=M1 + M2
As=As1 + As2
M1
1
fc
(bf
b)hf (h0
hf 2
)
As1
1
fc (bf fy
b)hf
M2 M M1
s2
M2
1 fcbh02
2
As2
1 fcb2h0
fy
但对于更高强度的钢材由于受砼极限压应变
的限值, fy'最多为400N/mm2。
20
4.5.3 基本公式的应用
截面设计 截面复核 截面设计：
又可分As和As均未知的情况I和已知As 求As‘的情况II。
21
情况I: 已知, bh, fcm, fy, fy ' 求As及As'
解: • 验算是否能用单筋: Mmax= α1fc bh02b(10.5b)
或
M = As fy h0(1－ 0.5)
15
令 s = (10.5)
s = 10.5 , s, s之间存在一一对应的关系, 可预先制
成表待查, 因此对于设计题：
s
M
1 fcbh02
对于校核题：
As
1 fcbh0
fy
As fy 1 fcbh0
s (1 0.5 )
Mu 1 fcbh02s
16
As bh0
min和x
xb (或
b )
• 若Mu M，则结构安全
当 < min Mu = Mcr = m ftw0
当 x > xb Mu = Mmax = α1fcbh02b(1-0.5b)

Mu
xc
C
Z
x 0 T C
xt
h0
Tc T s
M 0
M u TZ CZ
设AS—钢筋的面积；fy—钢筋的屈服强度，T= ASfy 。 Z和C与压区高度及压区应力分布有关。
第四节
单筋矩形截面受弯构件正截面承载力计算
b x h
一、计算基本公式及适用条件
基本公式 h0 受弯构件正截面承载能力计算，应满足作用 在结构上的荷载在结构截面中产生的弯矩设计 值M不超过按材料的强度设计值计算得到的受 as 弯构件承载能力设计值Mu， 即：M ≤ Mu
h0——截面有效高度， h0=h-as h——截面高度 as ——受拉钢筋合力点至混凝土受拉边缘的距离，初步计算时，对 于C25～C45等级的混凝土，可按35mm（单排受拉筋）、60mm（双排受拉 筋）、20mm（平板）取值。
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
◆ 例题3-1
解：查表得： fc=9.6N/mm2 ，； fy=300N/mm2 ； ξb=0.55；截面有效 高度 h。＝500-40＝460mm ；纵向受拉钢筋按一排放置，则梁的有效 高度h0＝500—40＝460mm。 1.计算受压区高度x
f y As 300 804 x 125.6mm b h0 0.55 460 253mm 1 f cb 1.0 9.6 200
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
第四节 单筋矩形截面受弯构件正截面承载力计算 一、计算基本公式及适用条件
单筋矩形截面 仅在受拉区布置纵向受力钢筋的矩形截面 双筋矩形截面 同时在受拉区和受压区布置纵向受力钢筋的矩形截面

发生条件： ρmin.h/h0≤ρ≤ρb
c
c
c
c
MI
Mcr
MII
My
(Mu) MIII
t<ft
sAs
sAs t=ft(t =tu)
s<y
sAs
s= fyAs
y
(c=cu) c
fyAs s>y
1.适筋梁特点：
min.h/h0 max
• 一开裂, 砼应力由裂缝截面处的钢筋承担, 荷 载继续增加, 裂缝不断加宽。受拉钢筋屈服, 压区砼压碎
主页 目录 上一章 下一章 帮助
ห้องสมุดไป่ตู้
混凝土结构设计原理
第4章
§4.1 概 述
4.1.1几个基本概念
1.受弯构件:主要指各种类型的梁和板。 内力特点:截面上通常有弯矩和剪力共同作用。
２. 正截面：与构件计算轴线相垂直的截面。
３. 承载力计算公式： M ≤Mu
M —— 受弯构件正截面弯矩设计值； Mu——受弯构件正截面受弯承载力设计值。
宽度 ：b = 120、150、（180）、200、（220）、 250、300、350、…(mm)
高度：h=250、300、350、400、……、750、800、 900、…(mm)。
二、 截面尺寸和配筋构造
2. 板
c15mm d
分布钢筋
h0
h
d 6 ~ 12mm
h0 h 20
板厚的模数为10mm
主页 目录 上一章 下一章 帮助
混凝土结构设计原理
第4章
§4.3 正截面受弯承载力计算原则
4.3.1 基本假设
截面应变保持平面； 不考虑混凝土抗拉强度； 钢筋的应力-应变具有以下关系：

第4章受弯构件的正截面承载力4. 1选择题1. （ C ）作为受弯构件正截面承载力计算的依据。

A I a 状态；B ・n a 状态；C ・川a 状态; 第n 阶段；A ）作为受弯构件抗裂计算的依据。

I a 状态；n a 状态；P 兰 PmaxA • ©(1-0. 5©);B ・ ©(1 +0. 5©)； C. 1一0・ D ・ 1+0.5© ;7•受弯构件正截面承载力屮，对于双筋截面，下面哪个条件可以满足受压钢筋的屈服•受弯构件正截面承载力计算中，截面抵抗矩系数取值为：（A )oD . 2.(AB. D .3“( C ・川a 状态; 第n 阶段； D ）作为受弯构件变形和裂缝验算的依据。

I a 状态； n a 状态； 川a 状态； 第n 阶段； B. C .D•寻弯构件沪截面承载力计算基本公式的律立杲依抿哪种确坏形杰律立A. B. C. 少筋破坏; 适筋破坏; 超筋破坏; 界限破坏;D. •下列那个条件不能用来判断适筋破坏与超筋破坏的界限（巴沁;X 兰巴山o ； C. X 兰 2a.s ；C )oC. X >2且s ；X v2a s；受弯构件正截面承载力T形截面划分为两类截面的依据是 D ）。

中，（计算公式建立的基本原理不同；受拉区与受压区截面形状A.不同；B.破坏形态不同；混凝土受压区的形状不同；C.9.提高受弯构件正截面受弯能力最有效的方法是（A.提高混凝土强度等级；增加保护层厚度；增加截面高度；增加截面宽度；B.T形截面梁的正截面承载力计算屮，假定在受压区翼缘计算宽度范围内混凝土C・ AD・1 n 农的压应力分布是（A.均匀分布；按抛物线形分B.布；按三角形分布；部分均C.匀，部分不均匀分布；n B11・混凝土保护层厚度是指（A.纵向钢筋内表面到混凝土表面的距B.离；纵向钢筋外表面到混凝土表面的C.距离；箍筋外表面到混凝土表面的距D.离；纵向钢筋重心到混凝土表面的距12.在进行钢筋混凝土矩形截面双筋梁正截面承载力计算屮，若x<2a s,则说明)OA. 受压钢筋配置过多；B. 受压钢筋配置过少；C. 梁发生破坏时受压钢筋早已屈服;D. 截面尺卄卜卜十・4・2判断题1.混凝土保护层厚度越大越好。

3.2 梁板结构的一般构造
第4章 受弯构件正截面承载力
分布钢筋的作用：
抵抗混凝土收缩和温度变化所引起的内力； 浇捣混凝土时，固定受力钢筋的位置； 将板上作用的局部荷载分散在较大的宽度上，以便 使更多的受力钢筋参与工作； 对四边支撑的单向板，可承受在计算中没有考虑的 长跨方向上实际存在的弯矩。
板中单位长度上的分布钢筋，其截面面积不应小于 单位长度上受力钢筋截面面积的15%，且配筋率不宜小于 0.15%。间距不应大于250mm，直径不宜小于6mm。
4.2 梁板结构的一般构造
第4章 受弯构件正截面承载力
弯起钢筋 架立钢筋
腰筋
箍筋
纵向钢筋
梁的钢筋构造
梁中钢筋由纵向受力钢筋、弯起钢筋、箍筋和架立钢筋组 成，纵向受力钢筋的作用是承受由弯矩在梁内产生的拉力。 常用直径：10～32mm。 当h ≥ 300mm，直径不小于10mm；当h<300mm，直径 不小于8mm。
第4章 受弯构件正截面承载力
梁的配筋率ρ 很小，梁拉区开裂后，钢筋 应力趋近于屈服强度，即开裂弯矩Mcr趋近于拉 区钢筋屈服时的弯矩 My，这意味着第Ⅱ阶段的 缩短，当ρ 减少到当 Mcr=My 时，裂缝一旦出现，
钢筋应力立即达到屈服强度，这时的配筋百分
率ρ 称为最小配筋率ρ
min。
min b max
h0
h
第4章 受弯构件正截面承载力
正截面受弯的三种破坏形态
(1) 适筋破坏形态——破坏始自受拉区 钢筋的屈服
受拉钢筋先屈服，受压区混凝土后 压坏，破坏前有明显预兆——裂缝、变 形急剧发展，为“塑性破坏”。
(2) 超筋破坏形态——破坏始自受压混 凝土的压碎
受压区混凝土先压碎，钢筋不屈服， 破坏前没有明显预兆，为“脆性破坏”。 钢筋的抗拉强度没有被充分利用。