matlab与通信仿真_第三章 随机信号和数字基带仿真_图文
- 格式:pdf
- 大小:1.49 MB
- 文档页数:33



北京邮电大学世纪学院毕业设计(论文)题目基于Matlab的数字基带通信系统仿真学号学生姓名专业名称通信与信息工程所在系(院) 通信与信息工程系指导教师年月日北京邮电大学世纪学院毕业设计(论文)任务书备注1、由指导教师撰写,可根据长度加页,一式三份,教务处、系(院)各留存一份,发给学生一份,任务完成后附在论文内;2、凡审核不通过的任务书,请重新申报。
题目数字基带传输系统的仿真摘要本论文主要研究了数字信号的基带传输的基本概念及数字信号基带传输的传输过程和如何用MATLAB软件仿真设计数字基带传输系统。
本文首先介绍了MATLAB仿真软件。
然后介绍了本课题的理论依据,包括数字通信,数字基带传输系统的组成及数字基带信号的传输过程。
接着介绍了数字基带传输系统的特性包括数字PAM信号功率普密度及常用线路码型,并通过比较最终选择双极性不归零码。
之后介绍了数字基带信号的最佳接收的条件以及如何通过示波器观察基带信号的波形。
最后按照仿真过程基本步骤用MATLAB的仿真工具实现了数字基带传输系统的仿真过程,对系统进行了分析。
关键词数字基带传输系统 MATLAB 计算机仿真Title Digital Base Band Transmission System SimulationAbstractThis paper mainly studies the baseband transmission of digital signal and the basic concept of baseband transmission of digital signal in the transmission process and how to use MATLAB software to design and Simulation of digital baseband transmission system. This paper first introduces MATLAB simulation software. Then introduces the theoretical basis, including digital communication, digital baseband transmission system and digital baseband signal transmission process. Then it introduces the characteristics of digital baseband transmission system includes the digital PAM signal power spectrum density and commonly used line code, and through the comparison of the final choice of bipolar nrz. After introducing the digital baseband signal received by the best conditions and how the baseband signal waveform oscilloscope observation. Finally, in accordance with the basic steps of simulation process using MATLAB simulation tool to achieve the digital baseband transmission system simulation process, has carried on the system analysis.Keywords Digital Base Band Transmission System Computer simulation1.序论 (1)1.1 数字基带传输系统概述 (1)2. MATLAB基本知识 (4)2.1 MATLAB简介 (4)2.2 MATLAB特点 (4)2.3 MATLAB优势 (5)2.4 MATLAB常用函数 (7)2.5 MATLAB常用工具箱 (8)3.数字基带传输系统的简介 (10)3.1 研究意义 (10)3.2数字基带传输系统 (10)3.2.1 基带传输系统简介 (10)3.2.2 基带传输系统结构图 (11)3.2.3 基带传输过程 (11)4.综合研究基带传输系统的特性 (13)4.1数字PAM信号 (13)4.2数字PAM信号功率谱密度 (14)4.2.1单极性不归零码(NRZ) (14)4.2.2 双极性不归零码 (15)4.2.3 单极性归零码(RZ) (15)4.2.4双极性归零码 (16)4.2.5差分码(相对码) (17)4.3常用线路码型 (18)4.3.1 AMI码 (19)4.3.2 HDB3码 (19)4.3.3 CMI码 (20)4.3.4 数字双向码 (20)4.4数字基带信号的最佳接收 (20)4.5带限系统下的基带信号 (21)4.5.1 抽样点无码间干扰的基带成型 (21)4.5.2 升余弦滚降系统 (21)4.5.3 最佳基带系统 (21)4.5.4 基带信号眼图 (22)4.6 部分响应系统 (24)5.基带传输系统的设计及仿真 (25)5.1随机信号的产生 (26)5.1.1 高斯噪声的产生 (26)5.1.2 随机码序列的产生 (26)5.1.3 产生数字基带信号的一般方法 (26)5.1.4 NRZ及RZ信号的产生 (27)5.1.5 眼图 (28)5.2 误码率 (28)5.2.1取样判决 (28)5.2.2 误码率测量 (28)5.4 实验结果 (29)6.通信系统发展前景 (31)6.1 3G技术 ...................................................................................................... 错误!未定义书签。

第2-1页Matlab与通信仿真主讲教师:和煦通信基础实验教学中心第2-2页内容提要Matlab基础知识1Matlab计算结果可视化和确知信号分析23模拟调制Matlab实现4模拟信号的数字传输5数字频带传输系统6通信系统仿真综合实验7随机信号和数字基带仿真本章目标•掌握库函数产生随机数方法•理解采用蒙特卡罗算法仿真的思想•基带信号波形生成和其功率谱密度第2-3页3.1随机信号产生与功率谱密度基本原理•(1)库函数产生随机数•均匀分布的随机数——rand函数产生(0,1)内均匀分布的随机数•1)x=rand(m);•2)x=rand(m,n);•3)x=rand;第2-4页•高斯分布的随机数——randn函数产生均值为0,方差为1的高斯分布的随机数。
•1)x=randn(m);•2)x=randn(m,n);•3)x=randn第2-5页•例3-1产生一个(0,1)上均匀分布的白噪声信号u(n),画出其波形,并检验其分布。
•clc,clear; %清除内存中可能保留的MATLAB变量•N=500000; %u(n)的长度•u=rand(1,N); %调用rand,得到均匀分布的随机数u(n)•u_mean=mean(u); %求u(n)均值•power_u=var(u); %求u(n)方差•subplot(211)•plot(u(1:100));grid on;%在一个图上分上下两个子图•ylabel('u(n) '); %给y轴加坐标•xlabel('n'); %给x轴加坐标•subplot(212)•hist(u,50);grid on;•%对u(n)做直方图,检验其分布,50是对取值范围[0 1]均分等分50份。
•ylabel('histogram of u(n)');第2-6页第2-7页02040608010000.20.40.60.81u (n ) n 00.20.40.60.81050001000015000h i s t o g r a m o f u (n )应如何表示?•如果x是(0,1)内均匀分布的随机信号,那么u=cx+d第2-8页•例3-2 产生一个均值为0.01,功率为0.1的均匀分布的白噪声信号u(n),画出其波形。
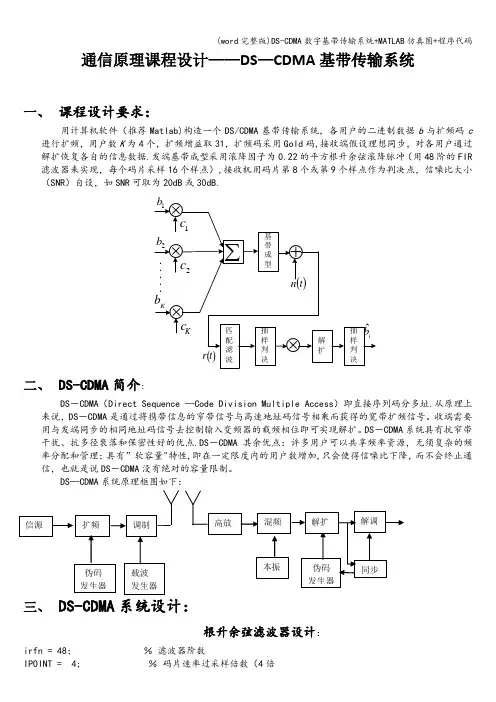
通信原理课程设计——DS —CDMA 基带传输系统一、 课程设计要求:用计算机软件(推荐Matlab)构造一个DS/CDMA 基带传输系统,各用户的二进制数据b 与扩频码c 进行扩频,用户数K 为4个,扩频增益取31,扩频码采用Gold 码,接收端假设理想同步,对各用户通过解扩恢复各自的信息数据.发端基带成型采用滚降因子为0.22的平方根升余弦滚降脉冲(用48阶的FIR 滤波器来实现,每个码片采样16个样点),接收机用码片第8个或第9个样点作为判决点,信噪比大小(SNR )自设,如SNR 可取为20dB 或30dB.⊗⊗⊗12b二、 DS-CDMA 简介:三、 DS-CDMA 系统设计:根升余弦滤波器设计:irfn = 48; % 滤波器阶数IPOINT = 4; % 码片速率过采样倍数(4倍alfs = 0.22;%滚降因子[xh] = hrollfcoef(irfn,IPOINT,sr,alfs,1);%发送端根升余弦滤波器系数[xh2] = hrollfcoef(irfn,IPOINT,sr,alfs,0);%接收端根升余弦滤波器系数%根升余弦滤波器figure('Name’,’根升余弦滤波器’,'NumberTitle','on');% Txsubplot(211);stem(xh);grid;xlabel(’Bits index’);title(’发送端根升余弦滤波器');% Rxsubplot(212);stem(xh2);grid;xlabel('Bits index’);title(’接收端根升余弦滤波器’);误码率-信噪比关系图figure; % plot the BER vs。
SNRsemilogy(SNR,r,'r—x’),grid;xlabel('SNR’);ylabel(’BER’);title('BER vs. SNR’);原始数据,发送和接收的比较figure('Name','Original Data','NumberTitle',’on’);% plot data for a randomly selected user such as user no. 1 before the BPSK mapping Tx and Rx% Txsubplot(211);stem(data(cuser,1:20),’filled');grid;xlabel(’Bits index’);title('Transmitted Bits (showing only 20 bits)');% Rxsubplot(212);stem(data_rm(cuser,1:20),'filled');grid;xlabel('Bits index’);title('Received Bits (showing only 20 bits)’);BPSK编码后,发送和接收的比较figure(’Name',’BPSK Symbols’,’NumberTitle’,'on');% plot data for a randomly selected user such as user no. 1 after the BPSK mapping Tx andRx% Txsubplot(211);stem(data_m(cuser,1:20),'filled');grid;xlabel('Symbol index');title(’Transmitted BPSK Symbols (showing only 20 Symbol)');% Rxsubplot(212);stem(data_rs(cuser,1:20),’filled’);grid;xlabel('Symbol index');title(’Received BPSK Symbols (showing only 20 Symbol)’);要发送的数据,各个用户对应位求和的结果figure(’Name','Combined signals’,’NumberTitle','on');%plot combined signals %Txsubplot(211);stem(data_f(1:50),’filled');title('Combined signals (only 20 symbols)');xlabel('Index of Combined symbols’);ylabel('Magnitude’);grid;%Rxsubplot(212);stem(data_ros(1:50),’filled');title('Combined noisy signals (only 20 symbols)');xlabel(’Index of Combined symbols’);ylabel(’Magnitude’);四、心得体会:通过这一次通信原理课程设计,加深了对数字基带传输系统的认识,对于DS-CDMA传输系统又有了进一步的了解,原来学书本知识的时候感觉懵懵懂懂的,只记得几个公式而已,但是通过这一次实际操作才真正理解到了数字基带传输系统的深刻内涵.通过仿真结果中的波形、频谱图等直观的方式,有助于实现对DS—CDMA 系统规律的把握研究.通信系统的性能分析和仿真,随着通信技术、信息技术和计算机技术的发展以及网络系统的大量应用,显得越来越重要.利用通信仿真定量地进行通信的分析与评价,为设计和规划通信提供了重要的依据。

MATLAB仿真在基带传输教学中的应用Application of MATLAB in Base Band Transmission TeachingLI Le(College of Computer Science and technology, Southwest University of Scinece and Technology, Mianyang 621010, China) Abstract: According to the character of the course of base band transmission, A method was proposed in this paper that take MATLAB/Simulink as tool to solve some issues during the course. Then display the process of base band transmission simulation.数字信号的基带传输是通信系统中的一个重要环节,对基带传输研究的意义在于现代通信系统中广义上的任一线性调制的频带传输系统均可等效为基带传输系统,即数字基带传输中本就包含了频带传输的一些基本问题。
同时,就数字基带传输自身而言,随着数字通信技术的发展也被越来越多的应用[1]。
在基带传输理论学习过程中涉及到的信道编码、传输信道特性、接收滤波、抽样判决等环节存在较为抽象不易理解的问题,如果不经过实践环节,这些抽象的计算和变换难以较快的掌握。
但对于非通信专业的课程教学而言,通常缺乏专用的仪器或者实验设备来支撑这个实践环节的运作。
MATLAB是一款功能强大的工程技术数值运算跨平台语言,利用它的通信工具箱和可视化仿真模型库Simulink可有效实现通信系统的仿真。
Simulink可对动态系统进行建模、仿真并对仿真结果进行分析,其可视化建模的特点尤其适合于通信系统仿真等工作[2]。

实验一2:for i=1:50,j=1:50;A(i,j)=i+j-1;endC=flipud(A),B=fliplr(A),A(1:10,1:10)=zeros;D=A3:clear;a=255*rand(50);disp(a),a(find(a<128))=0;a(find(a>128))=255;w=a;disp(w)实验二:1:(1)clear;n=0:23;N=12;y1=sin(2*4*pi*n/N);y2=sin(2*5*pi*n/N);y3=sin(2*7*pi*n/N);y4=sin(2*10*pi*n/N);plot(n,y1,'+r-',n,y2,'-.',n,y3,'k-',n,y4,'*g-');axis([0 25 -1 2 ]);xlabel('横轴n');ylabel('纵轴y');text(0.8,0.9,'y1');text(19.6,0.9,'y2');text(14,0.9,'y3');text(5,0.9,'y4');title('plot tu xing');legend('y1=sin(2*4*pi*n/N)','y2=sin(2*5*pi*n/N)','y3=sin(2*7*pi*n/N)','y4=sin(2*10*pi*n/N)')(2)clear;n=0:23;N=12;y1=sin(2*4*pi*n/N);y2=sin(2*5*pi*n/N);y3=sin(2*7*pi*n/N);y4=sin(2*10*pi*n/N);stem(n,y1,'+r-');hold on;stem(n,y2,'b-');hold on;stem(n,y3,'k-');hold on;stem(n,y4,'*g-');axis([0,25,-2,4]);xlabel('横轴n');ylabel('纵轴y');text(0.8,1.2,'y1');text(3,1.4,'y2');text(14,1.2,'y3');text(10.9,1.3,'y4');title('n from 0 to 23');legend('y1=sin(2*4*pi*n/N)','y2=sin(2*5*pi*n/N)','y3=sin(2*7*pi*n/N)','y4=sin(2*10*pi*n/N)') 2:clear all;N=input('input N=');T=1;fs=1/T;N_sample=128;dt=1/N_sample;t=0:dt:10*T-dt;n=-N:N;Fn=(-1/2)*sinc(n/2).*exp(-j*n*pi/2);Fn(N+1)=0;ft=zeros(1,length(t));for m=-N:N;ft=ft+ Fn(m+N+1)*exp(j*m*pi*2*fs*t);endplot(t,ft);legend('时域曲线ft=ft+ Fn(m+N+1)*exp(j*m*pi*2*fs*t)',4)3:N_sample=128;dt=1/N_sample;t=0:dt:1-dt;st=[ones(1,N_sample/2),-ones(1,N_sample/2)];subplot(311);plot(t,st);axis([0 1 -2 2]);xlabel('t');ylabel('s(t)'); subplot(312);[f,sf]=T2F(t,st);plot(f,abs(sf));hold on;axis([-10 10 0 1]);xlabel('f');ylabel('|S(f)|');sff=(-1/2)*exp(-j*f*pi/2).*sinc(f/2);plot(f,abs(sff));[t,st]=F2T(f,sf);subplot(313);axis([0 1 -2 2]);xlabel('t');ylabel('恢复的s(t)');plot(t,st)子函数:(1):function[t,st]=F2T(f,sf)df=f(2)-f(1);Fmx=f(end)-f(1)+df;dt=1/Fmx;N=length(sf);T=dt*N;t=0:dt:T-dt;sff=fftshift(sf);st=Fmx*ifft(sff);(2):function[f,sf]=T2F(t,st)dt=t(2)-t(1);T=t(end);df=1/T;N=length(st);f=-N/2*df:df:N/2*df-df;sf=fft(st);sf=T/N*fftshift(sf);2图:M=4 M=5M=7 M=10M=4 M=5M=7 M=10N=10 N=10002468100246810实验三:1.(2)clear;p=2;N=5000;u=randn(5,4);c=sqrt(p);u=u*c;power_u=var(u);subplot(211)plot(u(1:20));grid on;ylabel('u(n)');xlabel('n');subplot(212)hist(u,50);grid on;ylabel('histogram of u(n)');2:clear all;N=500;disounce=(sign(rand(1,N)-0.5+eps)+1)/2; n=8;temp1=ones(1,n);temp0=zeros(1,n);new_disounce=[];for i=1:length(disounce)if disounce(i)==0new_disounce=[new_disounce temp0];elsenew_disounce=[new_disounce temp1];endendT=0.01;t=0:T/n:T/n*(length(new_disounce)-1);subplot(211);plot(t,new_disounce)axis([min(t)-0.1,max(t)+0.1,min(new_disounce)-0.1,max(new_disounce)+0.1]) y=new_disounce;Nf=length(t);Y=fft(y,Nf);Pyy=abs(Y).^2/Nf;dt=t(2)-t(1);df=1/dt;f=df*(0:(Nf-1)/2)/Nf;subplot(212);plot(f,10*log10(Pyy(1:((Nf-1)/2+1))));title('功率谱密度');xlabel('频率(HZ)');grid3:clear all;SNRindB1=0:1:12;SNRindB2=0:0.01:12;for i=1:length(SNRindB1)smld_err_prb(i)= exa0308_Fun_singlepe(SNRindB1(i));endsemilogy(SNRindB1,smld_err_prb,'r*');for i=1:length(SNRindB2)SNR=10^(SNRindB2(i)/10);theo_err_prb(i)=(1/2)*erfc(sqrt(SNR/2));endhold on;semilogy(SNRindB2,theo_err_prb);grid on子函数:function [p]=exa0308_Fun_singlepe(snr_in_dB)E=1;SNR=10^(snr_in_dB/10);sgma=E/sqrt(SNR*2);N=10000;dsource=(sign(rand(1,N)-0.5+eps)+1)/2;numoferr=0;for i=1:Nif (dsource(i)==0)r=-E+sgma*randn;elser=E+sgma*randn;endif(r<0.5*E)decis=0;elsedecis=1;endif (decis~=dsource(i)) numoferr=numoferr+1; end end p=numoferr/N;:实验3的图 1:>> x=2*rand(5,4) x =0.7375 1.9921 0.9260 0.5703 1.3593 1.8842 0.2846 1.5663 0.0472 1.6797 0.9457 1.9128 0.8051 0.0293 0.9237 0.82740.8319 1.4452 1.7069 0.359802468101214161820-4-2024u (n )nu =-1.2765 1.1282 0.4296 -1.4450 -1.3768 0.7019 1.3848 -3.8243 -1.9091 -1.3563 1.7813 -2.9299 -0.8431 0.1011 0.4232 0.9075 0.4459 0.3491 -1.6545 0.89682:0.20.40.60.811.21.41.61.820.51050100150200250300350400-400-200200功率谱密度频率(HZ)3:0246810121010101010100。

目录前言 (1)正文 (1)2.1数字基带传输系统 (1)2.2数字基带信号 (2)2.2.1基本的基带信号波形 (2)2.2.2基带传输的常用码型 (3)2.3实验原理 (5)2.3.1数字通信系统模型 (5)2.3.2数字基带传输系统模型 (6)2.4MATLAB软件简介 (7)2.4.1软件介绍 (7)2.4.2Matlab语言的特点 (8)Matlab语言有如下的特点: (8)2.5实验内容 (8)2.5.1理想低通特性 (8)2.5.2余弦滚降特性 (9)2.5.3Matlab设计流程图 (9)2.5.4余弦滚降系基于matlab的程序及仿真结果 (10)致谢 (12)参考文献 (13)附录 (14)前言与模拟通信相比,数字通信具有许多优良的特性,它的主要缺点就是设备复杂并且需要较大的传输带宽。
近年来,随着大规模集成电路的出现,数字系统的设备复杂程度和技术难度大大降低,同时高效的传输压缩技术以及光纤等大容量传输介质的使用正逐步使带宽问题得到了解决。
因此,数字传输方式日益受到欢迎。
通信原理计算机仿真实验,是对数字基带传输系统的仿真。
仿真工具是MATLAB程序设计语言。
MATLAB是一种先进的高技术程序设计语言,主要用于数值计算及可视化图形处理。
特点是将数值分析、矩阵计算、图形、图像处理和仿真等诸多强大功能集成在一个极易使用的交互式环境中伪科学研究、工程设计以及必须进行有效数值计算的众多学科提供了一种高效率的编程工具。
运用MATLAB,可以对数字基带传输系统进行较为全面地研究。
为了使本科类学生学好通信课程,我们进行了试点,通过课程设计的方式针对通信原理的很多内容进行了仿真。
正文2.1数字基带传输系统数字处理的灵活性使得数字传输系统中传输的数字信息既可以来自计算机,电传机等数据终端的各种数字代码,也可以来自模拟信号经数字化处理后的脉冲编码(PCM)信号等。
在原理上,数字信息可以直接用数字代码序列表示和传输,但在实际传输中,视系统的要求和信道情况,一般需要进行不同方式的编码,并且选用一组取值有限的离散波形来表示。

用MatLab仿真通信原理系列实验一、引言通信原理是现代通信领域的基础理论,通过对通信原理的研究和仿真实验可以更好地理解通信系统的工作原理和性能特点。
MatLab作为一种强大的数学计算软件,被广泛应用于通信原理的仿真实验中。
本文将以MatLab为工具,介绍通信原理系列实验的仿真步骤和结果。
二、实验一:调制与解调1. 实验目的通过MatLab仿真,了解调制与解调的基本原理,并观察不同调制方式下的信号特征。
2. 实验步骤(1)生成基带信号:使用MatLab生成一个基带信号,可以是正弦波、方波或任意复杂的波形。
(2)调制:选择一种调制方式,如调幅(AM)、调频(FM)或相移键控(PSK),将基带信号调制到载波上。
(3)观察调制后的信号:绘制调制后的信号波形和频谱图,观察信号的频谱特性。
(4)解调:对调制后的信号进行解调,还原出原始的基带信号。
(5)观察解调后的信号:绘制解调后的信号波形和频谱图,与原始基带信号进行对比。
3. 实验结果通过MatLab仿真,可以得到不同调制方式下的信号波形和频谱图,观察到调制后信号的频谱特性和解调后信号的还原效果。
可以进一步分析不同调制方式的优缺点,为通信系统设计提供参考。
三、实验二:信道编码与解码1. 实验目的通过MatLab仿真,了解信道编码和解码的基本原理,并观察不同编码方式下的误码率性能。
2. 实验步骤(1)选择一种信道编码方式,如卷积码、纠错码等。
(2)生成随机比特序列:使用MatLab生成一组随机的比特序列作为输入。
(3)编码:将输入比特序列进行编码,生成编码后的比特序列。
(4)引入信道:模拟信道传输过程,引入噪声和干扰。
(5)解码:对接收到的信号进行解码,还原出原始的比特序列。
(6)计算误码率:比较解码后的比特序列与原始比特序列的差异,计算误码率。
3. 实验结果通过MatLab仿真,可以得到不同编码方式下的误码率曲线,观察不同信道编码方式对信号传输性能的影响。

湘潭大学通信原理实验报告书课程名称:通信原理实验一:数字基带传输系统的MATLAB仿真实验二:模拟信号幅度调制仿真实验学生姓名:学号:班级:指导教师:王仕果2012年12 月实验一数字基带传输系统的MATLAB仿真一、实验目的:1、熟悉和掌握常用的用于通信原理时域仿真分析的MATLAB函数;2、掌握连续时间和离散时间信号的MATLAB产生;3、牢固掌握冲激函数和阶跃函数等函数的概念,掌握卷积表达式及其物理意义,掌握卷积的计算方法、卷积的基本性质;4、掌握利用MATLAB计算卷积的编程方法,并利用所编写的MATLAB程序验证卷积的常用基本性质;5、掌握MATLAB描述通信系统中不同波形的常用方法及有关函数,并学会利用MATLAB求解系统功率谱,绘制相应曲线。
二、实验内容1、编写MATLAB程序产生离散随机信号2、编写MATLAB程序生成连续时间信号3、编写MATLAB程序实现常见特殊信号三、实验原理:从通信的角度来看,通信的过程就是消息的交换和传递的过程。
而从数学的角度来看,信息从一地传送到另一地的整个过程或者各个环节不外乎是一些码或信号的交换过程。
例如信源压缩编码、纠错编码、AMI编码、扰码等属于码层次上的变换,而基带成形、滤波、调制等则是信号层次上的处理。
码的变换是易于用软件来仿真的。
要仿真信号的变换,必须解决信号与信号系统在软件中表示的问题。
3.1 信号及系统在计算机中的表示3.1.1 时域取样及频域取样一般来说,任意信号s(t是定义在时间区间(-∞,+∞)上的连续函数,但所有计算机的CPU都只能按指令周期离散运行,同时计算机也不能处理(-∞,+∞)这样一个时间段。
为此将把s(t按区间,22TT⎡⎤−⎢⎥⎣⎦截短为sT(t,再对sT(t按时间间隔Δt均匀取样,得到取样点数为:TNtt=Δ (3-1仿真时用这个样值集合来表示信号s(t。
显然Δt反映了仿真系统对信号波形的分辨率,Δt越小,则仿真的精确度越高。

通信原理上机实验报告年级:姓名:学号:时间:数字基带信号波形仿真一、实验目的1.熟悉MATLAB软件的工作环境二、实验原理数字基带信号的波形经常采用方波,其中最基本的二进制基带信号波形有单极性归零波形、单极性不归零波形、双极性归零波形、双极性不归零波形。
三、实验内容与结果(1)数字基带信号波形的MATLAB仿真下面通过MATLAB程序来仿真一串随机消息代码的基带信号波形、首先产生1000个随机信号序列,分别用单极性归零码、单极性不归零码、双极性归零码和双极性不归零码编码,并且求平均功率谱密度。
源代码(以双极性为例)如下:close allclear allk=14;L=32;N=2^k;M=N/L;dt=1/L;T=N*dt;df=1.0/T;Bs=N*df/2;t=linspace(-T/2,T/2,N);f=linspace(-Bs,Bs,N);EP1=zeros(size(f));EP2=zeros(size(f));EP3=zeros(size(f));for x=1:1000k=round(rand(1,M));nrz=zeros(L,M);rz=zeros(L,M);for i=1:Mif k(i)==1nrz(:,i)=1;elsenrz(:,i)=-1;rz(1:L/2,i)=-1;endendnrz=reshape(nrz,1,N);rz=reshape(rz,1,N);NRZ=t2f(nrz,dt);P1=NRZ.*conj(NRZ)/T;RZ=t2f(rz,dt);P2=RZ.*conj(RZ)/T;EP1=(EP1*(x-1)+P1)/x;EP2=(EP2*(x-1)+P2)/x;endfigure(1)subplot(2,2,1);plot(t,nrz)axis([-5,5,min(nrz)-0.1,max(nrz)+0.1])title('Ë«¼«ÐÔ²»¹éÁãÂë','fontsize',12)xlabel('t(ms)','fontsize',12)ylabel('nrz(t)','fontsize',12)grid onsubplot(2,2,2);plot(t,rz)axis([-5,5,min(rz)-0.1,max(rz)+0.1])title('Ë«¼«ÐÔ¹éÁãÂë','fontsize',12)xlabel('t(ms)','fontsize',12)ylabel('rz(t)','fontsize',12)grid onsubplot(2,2,3);plot(f,EP1)axis([-5,5,0,1.2])title('Ë«¼«ÐÔ²»¹éÁãÂ빦ÂÊÆ×ÃܶÈͼ','fontsize',12) xlabel('f(kHz)','fontsize',12)ylabel('P1(f)','fontsize',12)grid onsubplot(2,2,4);plot(f,EP2)axis([-5,5,0,0.3])title('Ë«¼«ÐÔ¹éÁãÂ빦ÂÊÆ×ÃܶÈͼ','fontsize',12) xlabel('f(kHz)','fontsize',12)ylabel('P2(f)','fontsize',12)grid on调用傅里叶变换的函数t2f,该函数定义如下:function X=t2f(x,dt)X=fftshift(fft(x))*dt;end(1)实验结果1.数字基带信号波形的Simulink仿真(1)Simulink仿真模型(2)数字基带信号波形的Simulink仿真参数(3)实验结果。
姓名:范浩如学号:107551400879数字通信作业:二进制调制最佳接收机的matlab仿真第一章基础理论知识第一节知识框架图第二节数字基带信号传输模型第一步:对原始数字序列进行调制典型的调制方法键控开关载波cos(w0t)输入数字序列1001得到2ASK信号第二步:调制信号在信道中的传输第三步:调制型号的解调(相干解调法) 方法一:针对2ASK,2PSK 信号进行接收与解调 判决门限:2ASK 0.5A 2PSK 0乘法器相干信号Cos(w 0t)从信道中接收的信号低通滤波器带通滤波抽样判决从接收信号中分解出频率滤除带外噪声频域向左右移动w0频率滤除2w0处的信号得到抽样频率得到原始数字序列方法二:针对2FSK信号进行接收与解调判决门限:比较两路信号,谁大选谁。
或者将两路信号相减,然后以0为判决门限。
大于0时为1(W1代表的),小于0时为0(W0代表的)第二章Matlab程序与仿真:第一节理想信噪比-误码率曲线的产生N=10;k0=2;Th1=0;A=1; %设置基本参量for db=-5:0.2:15 %设置信噪比范围(取101个点)r=10^(db/10); %对数化后的信噪比ri0=round((db+6)*5-4); %数组序号必须从1开始pe0ASKa(i0)=0.5*erfc(sqrt(r/2));%理想条件下Ask的误码率(a)非相干pe0ASKb(i0)=0.5*erfc(sqrt(r/4));%理想条件下Ask的误码率(b)相干pe0FSK(i0)=pe0ASKa(i0); %理想条件下Fsk的误码率pe0PSK(i0)=0.5*erfc(sqrt(r)); %理想条件下psk的误码率i=1:0.2:21;i1=i-6; %设置i1的范围从-5到15endsemilogy(i1,pe0PSK,'b',i1,pe0ASKb,'b',i1,pe0FSK,'b');axis([-5 15 1.0e-06 1.0e0])第二节 2Ask信号的调制解调Matlab程序:Test=[0,1,0,0,0,0,1,1,1,0,0,1,1,1,1,0,1,1,1,1,0,1,1,1,0,0,1,1,1, 1,1,0,1,1,1,0,1,1,1,1,1,0,0,0,1,1,1,1,0,1,]for db=-5:0.2:15sigma=0.5*A*sqrt(N)/10^(db/20); %设置噪声功率Th=0.5*0.5*A^2*N; %2ASK的判决门限count=0;for j=1:50; %取50个样本for i=1:Nrand('state',sum(100*clock)); %将时钟作为产生随机信号的种子NN(i)=sigma*randn(1,1); %产生随机高斯噪声s0(i)=0; %输入端0码元波形s1(i)=A*sin(2*pi*k0*i/N); %输入端1码元波形x0(i)=s0(i)+NN(i); %接收端0码元波形x1(i)=s1(i)+NN(i); %接收端1码元波形endsumm0=0;if test(j)==0for i=1:Nsumm0=summ0+x0(i)*s1(i);endelseif test(j)==1for i=1:Nsumm0=summ0+x1(i)*s1(i);endendsumma=summ0;Th=0.5*0.5*A^2*N; %2ASK的判决门限if summa>Th %和门限值进行比较 out(i0,j)=1elseout(i0,j)=0endif test(j)==out(i0,j)elsecount=count+1;endendpeASK(i0)=count/L;End测试结果如下:原始输入序列test1-20: 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 121-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 141-50: 1 0 0 0 1 1 1 1 0 1信噪比db=-5时,out(1,:) 错误码元数:171-20: 0 1 0 1 0 1 1 1 0 0 1 0 0 0 0 0 0 0 1 021-30: 1 1 0 1 0 0 1 1 1 1 0 1 1 1 1 0 1 0 1 141-50: 1 1 0 1 1 1 1 1 1 1Ps:传错的码加下划线信噪比db=5时,out(51,:) 错误码元数:11-20: 0 1 0 0 1 0 1 1 1 0 0 1 1 1 1 0 1 1 1 121-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 41-50: 1 0 0 0 1 1 1 1 0 1信噪比db=15时,out(101,:) 错误码元数:01-20: 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 121-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 41-50: 1 0 0 0 1 1 1 1 0 1测试集大小为1000时的信噪比-误码率曲线第三节 2psk信号的调制解调程序基本上和上面一个相同,只是输入端码元改变为:s0(i)=A*sin(2*pi*k0*i/N); %输入端0码元S1(i)=-A*sin(2*pi*k0*i/N); %输入端1码元门限值改变为: Th=0;测试结果如下:原始输入序列test1-20: 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 1 21-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 41-50: 1 0 0 0 1 1 1 1 0 1信噪比db=-5时,out(1,:) 错误码元数:81-20: 0 1 1 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 0 21-30: 0 0 1 1 0 0 0 1 1 1 1 1 1 1 0 0 1 1 0 0 41-50: 1 0 0 0 1 1 1 1 0 1信噪比db=5时,out(51,:) 错误码元数:11-20: 0 1 0 0 0 0 1 1 1 0 0 1 0 1 1 0 1 1 1 1 21-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 141-50: 1 0 0 0 1 1 1 1 0 1信噪比db=15时,out(101,:) 错误码元数:01-20: 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 121-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 41-50: 1 0 0 0 1 1 1 1 0 1测试集大小为1000时的信噪比-误码率曲线第四节 2Fsk信号的调制解调for j=1:50, %取50个样本for i=1:NNN(i)=sigma*randn(1,1); %产生随机高斯噪声 s0(i)=A*sin(2*pi*k0*i/N); %输入端0码元s1(i)=A*sin(2*pi*(k0+1)*i/N); %输入端1码元x0(i)=s0(i)+NN(i); %接收端0码元波形 x1(i)=s1(i)+NN(i); %接收端1码元波形endsumm0=0;summa=0;summb=0;if test(j)==0for i=1:Nsumma=summa+x0(i)*s0(i);summb=summb+x1(i)*s0(i);endelseif test(j)==1for i=1:Nsumma=summa+x0(i)*s1(i);summb=summb+x1(i)*s1(i);endendsumm0=summa-summb;Th=0;if summ0>Th %和门限值进行比较out(i0,j)=0elseout(i0,j)=1endif test(j)==out(i0,j)elsecount=count+1;endendpePSK(i0)=count/L;end测试结果如下:原始输入序列test1-20: 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 1 21-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 1 41-50: 1 0 0 0 1 1 1 1 0 1信噪比db=-5时,out(1,:) 错误码元数:71-20: 0 1 0 0 0 0 1 1 0 0 0 1 1 1 0 0 1 1 1 121-30: 0 1 1 1 0 0 1 1 1 1 1 0 0 0 1 0 1 0 1 141-50: 1 1 0 0 1 1 1 1 1 1信噪比db=5时,out(51,:) 错误码元数:01-20: 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 1 21-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 141-50: 1 0 0 0 1 1 1 1 0 1信噪比db=15时,out(101,:) 错误码元数:01-20: 0 1 0 0 0 0 1 1 1 0 0 1 1 1 1 0 1 1 1 121-30: 0 1 1 1 0 0 1 1 1 1 1 0 1 1 1 0 1 1 1 141-50: 1 0 0 0 1 1 1 1 0 1测试集大小为1000时的信噪比-误码率曲线第三章数据分析与总结本次试验采用的样本集数量为50,1000两种。
基带信号眼图实验——matlab 仿真————————————————————————————————作者:————————————————————————————————日期:ﻩ数字基带信号的眼图实验——matla b仿真一、实验目的1、掌握无码间干扰传输的基本条件和原理,掌握基带升余弦滚降系统的实现方法;2、通过观察眼图来分析码间干扰对系统性能的影响,并观察在输入相同码率的NRZ 基带信号下,不同滤波器带宽对输出信号码间干扰大小的影响程度;3、熟悉MATL AB 语言编程。
二、实验预习要求1、复习《数字通信原理》第七章7.1节——奈奎斯特第一准则内容;2、复习《数字通信原理》第七章7.2节——数字基带信号码型内容;3、认真阅读本实验内容,熟悉实验步骤。
三、实验原理和电路说明1、基带传输特性基带系统的分析模型如图3-1所示,要获得良好的基带传输系统,就应该()nsna t nT δ-∑()H ω()nsna h t nT -∑基带传输抽样判决图3-1ﻩ基带系统的分析模型抑制码间干扰。
设输入的基带信号为()nsna t nT δ-∑,sT 为基带信号的码元周期,则经过基带传输系统后的输出码元为()nsna h t nT -∑。
其中1()()2j th t H ed ωωωπ+∞-∞=⎰ﻩ(3-1)理论上要达到无码间干扰,依照奈奎斯特第一准则,基带传输系统在时域应满足:10()0,s k h kT k =⎧=⎨⎩,为其他整数 ﻩﻩ ﻩ(3-2)频域应满足:()0,ss T T H πωωω⎧≤⎪=⎨⎪⎩,其他 ﻩ ﻩ(3-3)ωsT ()H ωsT πsT π-图3-2 理想基带传输特性此时频带利用率为2/Baud Hz ,这是在抽样值无失真条件下,所能达到的最高频率利用率。
由于理想的低通滤波器不容易实现,而且时域波形的拖尾衰减太慢,因此在得不到严格定时时,码间干扰就可能较大。
在一般情况下,只要满足:222(),s i s s s si H H H H T T T T T ππππωωωωω⎛⎫⎛⎫⎛⎫+=-+++=≤⎪ ⎪⎪⎝⎭⎝⎭⎝⎭∑ﻩ (3-4)基带信号就可实现无码间干扰传输。
第2-1页Matlab与通信仿真主讲教师:和煦通信基础实验教学中心第2-2页内容提要Matlab基础知识1Matlab计算结果可视化和确知信号分析23模拟调制Matlab实现4模拟信号的数字传输5数字频带传输系统6通信系统仿真综合实验7随机信号和数字基带仿真本章目标•掌握库函数产生随机数方法•理解采用蒙特卡罗算法仿真的思想•基带信号波形生成和其功率谱密度第2-3页3.1随机信号产生与功率谱密度基本原理•(1)库函数产生随机数•均匀分布的随机数——rand函数产生(0,1)内均匀分布的随机数•1)x=rand(m);•2)x=rand(m,n);•3)x=rand;第2-4页•高斯分布的随机数——randn函数产生均值为0,方差为1的高斯分布的随机数。
•1)x=randn(m);•2)x=randn(m,n);•3)x=randn第2-5页•例3-1产生一个(0,1)上均匀分布的白噪声信号u(n),画出其波形,并检验其分布。
•clc,clear; %清除内存中可能保留的MATLAB变量•N=500000; %u(n)的长度•u=rand(1,N); %调用rand,得到均匀分布的随机数u(n)•u_mean=mean(u); %求u(n)均值•power_u=var(u); %求u(n)方差•subplot(211)•plot(u(1:100));grid on;%在一个图上分上下两个子图•ylabel('u(n) '); %给y轴加坐标•xlabel('n'); %给x轴加坐标•subplot(212)•hist(u,50);grid on;•%对u(n)做直方图,检验其分布,50是对取值范围[0 1]均分等分50份。
•ylabel('histogram of u(n)');第2-6页第2-7页02040608010000.20.40.60.81u (n ) n 00.20.40.60.81050001000015000h i s t o g r a m o f u (n )应如何表示?•如果x是(0,1)内均匀分布的随机信号,那么u=cx+d第2-8页•例3-2 产生一个均值为0.01,功率为0.1的均匀分布的白噪声信号u(n),画出其波形。
•clc,clear;•P=0.1; % 希望的功率•mu=0.01; % 希望的均值•N=50000; % 序列长度•x=rand(1,N); % 生产N个[0,1]上均匀分布的随机序列x•temp=var(x); % x序列的方差•c=sqrt((P-mu^2)/var(x));% 求系数c•d=mu-c*mean(x); % 求系数d•u=c*x+d; % 求均值为ma、功率为P的随机序列u•mean_u=mean(u); % 求随机序列u的均值•power_u=dot(u,u)/N; % 求随机序列u的功率,检验u1(n)的功率是否满足要求dot是matlab内部函数,实现两个向量的乘积,该句等效于var 第2-9页第2-10页•subplot(211);•plot(u(1:200));grid on;•ylabel('u(n)');•xlabel('n');•subplot(212);•hist(u,50);grid on;•%对u(n)做直方图,检验其分布,•%50是对取值范围[0 1]•%均分等分50份。
•ylabel('histogram of u(n)');050100150200-1-0.500.51u (n )n -0.8-0.6-0.4-0.200.20.40.6050010001500h i s t o g r a m o f u (n )第2-11页•例3-3 产生一个均值为0,方差为0.1,服从高斯分布的白噪声信号u(n),画出其波形.•clc,clear;•p=0.1;•N=500000;•u=randn(1,N);•a=sqrt(p);•u=u*a;•power_u=var(u);•subplot(211)•plot(u(1:200));grid on;•ylabel('u(n) '); •xlabel('n'); •subplot(212)•hist(u,50);grid on;•ylabel('histogram of u(n) ');050100150200-1-0.50.51u (n ) n-2-1.5-1-0.500.51 1.501234x 104h i s t o g r a m o f u (n )•例3-4 通过Matlab中的函数rand产生[0,1]均匀分布的随机变量,并用其产生一个0、1的随机序列,其中:0的概率为p=0.3。
•clc,clear;•p=0.3;•m=2;•n=2;•s=rand01(p,m,n)•%%%%%%%%%%%%%%%%%%%%%%%%•function s=rand01(p,m,n)%产生一个(p,1-p)的0-1随机变量,文件rand01.m•% 输入参数:•% p:0-1分布中1的概率•% m,n:产生的随机变量样本个数m×n•% 输出:产生的随机变量样本矢量•x=rand(m,n);•s=(sign(x-p+eps)+1)/2;% eps = 2^(-52).第2-12页•例3-5 通过Matlab中的函数randn产生σ2=2,N(0,1)的高斯随机变量,并用其产生的瑞利分布随机变量。
•解:可以证明,两个独立同分布、均值为0的高斯随机变量N(0,σ2 )的平方和开根号所得的随机变量服从功率为2σ2的瑞利分布。
•clc,clear;•sigma2=2;•m=2;•n=2;•s=rayleigh(sigma2,m,n)•%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%•function s=rayleigh(sigma2,m,n)•% 输入参数: sigma2,瑞利分布的功率;m,n: 输出m×n个样本•x=sqrt(sigma2/2)*randn(m,n);•y=sqrt(sigma2/2)*randn(m,n);•s=sqrt(x.*x+y.*y);第2-13页• 2 基带信号波形生成和其功率谱密度•要画出完整的波形,每一个码元要采 n个样,如果一个N个码元的0、1序列x,要画出它的矩形脉冲波形,可以用如下方法完成。
•例3-6 产生一个N码元,每码元采样n个的0、1序列。
•N=100; % 二进制序列的长度•dsource =(sign(rand(1,N)-0.5+eps)+1)/2; % 生成N码元的0、1序列•n=10; % 每周期采样数为10•temp1=ones(1,n); %表示1码•temp0=zeros(1,n); %表示0码•new_dsource=[];第2-14页•for i=1:length(dsource)•if dsource(i)==0•new_dsource=[new_dsource temp0];•else•new_dsource=[new_dsource temp1];•end•end•T=0.10; % 每码元周期•t=0:T/n:T/n*(length(new_dsource)-1); % 时间轴,new_dsource序号从1开始(length(new_dsource),而t是从0开始,故要减去1•plot(t,new_dsource)•axis([min(t)-0.01,max(t)+0.01,min(new_dsource)-0.01,max(new_dsource)+0.01]);第2-15页第2-16页024681000.10.20.30.40.50.60.70.80.91第2-17页•信号f(t)的功率谱密度•例题3-7 求叠加了高斯噪声的正弦信号的功率谱密度.•clc,clear;•t=0:0.001:0.6; %时域信号的时间范围•x=0.4*sin(2*pi*50*t)+0.4*sin(2*pi*320*t); %正弦信号•y=x+ randn(size(t)); %正弦信号+噪声•subplot(2,1,1);•plot(t(1:100),y(1:100));•title('0均值的随机信号')•xlabel('时间 (秒)')T F im l P T T 2)()(ωω∞→=•Nf=length(t);•Y=fft(y,Nf); %求有限长(正弦+噪声)信号的傅里叶变换•Pyy=abs(Y).^2/Nf; %求傅里叶变换模平方的均值•f=1000*(0:(Nf-1)/2)/Nf; %得到频率轴,1000=1/dt,频率区间长度,见第二章定义,这里只画出了正半轴,注意区间长度•subplot(2,1,2);•plot(f,Pyy(1:((Nf-1)/2+1)));%注意区间长度•title('信号的功率谱密度');•xlabel('频率(Hz)');第2-18页第2-19页00.020.040.060.080.1-4-2240均值的随机信号时间 (秒)0100200300400500010203040信号的功率谱密度频率(Hz)•例3-8 求单极性0、1随机序列的功率谱密度。
•clc,clear;•N=1000; %0、1序列长度•dsource =(sign(rand(1,N)-0.5+eps)+1)/2; %生成长度为N的0、1序列•n=10; %每码元采n=10个样值•temp1=ones(1,n);temp0=zeros(1,n);•new_dsource=[];•for i=1:length(dsource)• if dsource(i)==0• new_dsource=[new_dsource temp0];• else• new_dsource=[new_dsource temp1];• end•end第2-20页•T=0.10; %码元周期•t=0:T/n:T/n*(length(new_dsource)-1);%时间轴•subplot(2,1,1)•plot(t,new_dsource) %画生成的0、1随机序列的波形•axis([min(t)-0.01,max(t)+0.01,min(new_dsource)-0.01,max(new_dsource)+0.01])•y=new_dsource;•Nf=length(t);•Y = fft(y,Nf); %做FFT•Pyy=abs(Y).^2/Nf; %平均功率•dt=t(2)-t(1); df=1/dt; %频域延拓周期• f = df*(0:(Nf-1)/2)/Nf; %频率轴•subplot(2,1,2);•plot(f,10*log10(Pyy(1:((Nf-1)/2+1))))•title('功率谱密度');•xlabel('频率 (Hz)');•grid;第2-21页第2-22页02040608010000.20.40.60.8101020304050-100-5050功率谱密度频率 (Hz)3.2蒙特卡洛仿真第2-23页第2-24页•蒙特卡罗估计是指通过随机实验估计系统参数值的过程。