实验四 窄带随机信号的仿真与分析

随机信号分析实验报告——基于MATLAB语言姓名：_班级：_学号：专业：目录实验一随机序列的产生及数字特征估计 (2)实验目的 (2)实验原理 (2)实验内容及实验结果 (3)实验小结 (6)实验二随机过程的模拟与数字特征 (7)实验目的 (7)实验原理 (7)实验内容及实验结果 (8)实验小结 (11)实验三随机过程通过线性系统的分析 (12)实验目的 (12)实验原理 (12)实验内容及实验结果 (13)实验小结 (17)实验四窄带随机过程的产生及其性能测试 (18)实验目的 (18)实验原理 (18)实验内容及实验结果 (18)实验小结 (23)实验总结 (23)实验一随机序列的产生及数字特征估计实验目的1.学习和掌握随机数的产生方法。

2.实现随机序列的数字特征估计。

实验原理1.随机数的产生随机数指的是各种不同分布随机变量的抽样序列（样本值序列）。

进行随机信号仿真分析时，需要模拟产生各种分布的随机数。

在计算机仿真时，通常利用数学方法产生随机数，这种随机数称为伪随机数。

伪随机数是按照一定的计算公式产生的，这个公式称为随机数发生器。

伪随机数本质上不是随机的，而且存在周期性，但是如果计算公式选择适当，所产生的数据看似随机的，与真正的随机数具有相近的统计特性，可以作为随机数使用。

(0,1)均匀分布随机数是最最基本、最简单的随机数。

(0,1)均匀分布指的是在[0,1]区间上的均匀分布， U(0,1)。

即实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数，通常采用的方法为线性同余法，公式如下：，序列为产生的(0,1)均匀分布随机数。

定理1.1若随机变量X 具有连续分布函数，而R 为(0,1)均匀分布随机变量，则有2.MATLAB中产生随机序列的函数(1)(0,1)均匀分布的随机序列函数：rand用法：x = rand(m,n)功能：产生m×n 的均匀分布随机数矩阵。

(2)正态分布的随机序列函数：randn用法：x = randn(m,n)功能：产生m×n 的标准正态分布随机数矩阵。

实验报告实验题目：窄带随机过程的模拟窄带随机过程的模拟一、实验目的（1）了解具有任意功率谱（低频）的正态随机过程的模拟； （2）了解窄带随机过程的模拟方法。

二、实验原理（1）任意功率谱的正态随机过程的模拟假定需要产生一个持续时间为d T 的高斯随机过程的一个样本()X t ，要求功率谱满足()X G f 。

为此，可以先将()X t 进行周期延拓，得到一个周期信号，然后对周期信号进行傅里叶级数展开。

即0201()()j f k k k dXt X e f T π∞=-∞==∑由于傅里叶级数是k X 的线性组合，所以，如果k X 是零均值的高斯随机变量，那么()X t 也是零均值高斯过程，如果{}()Xt 是两两正交的序列，则周期信号的功率谱为线谱。

即 2220()()(())kk k X k G f g f kf gE X δ∞=-∞=- =∑通过选择k g 就可以得到期望的功率谱。

假定()X G f 是带限的，即()0()X G f f B = >那么，{}2k g 只有有限项，共21M +项，与此对应的傅里叶级数也是21M +项。

因此，只需产生21M +个互相正交的零均值高斯随机变量{}11,,,,M M M M X X X X --+- 。

然后据此构造时域样本函数即可，有02()[]()Mj f k i t k k MX i X i t X e π∆=-=∆=∑其中t ∆为任意小的时间间隔。

（2）窄带随机过程的模拟对于窄带系统，当系统输入白噪声或宽带噪声时，输出可以表示为0()()cos[()]Y t A t t t ω=+Φ其中0ω为中心频率，()A t 和()t Φ是满变化的随机过程，对上式展开得00()()cos ()sin c s Y t A t t A t t ωω=-其中，()()cos (),()()sin ()c s A t A t t A t A t t =Φ=Φ，是慢变化的随机过程，分别称为窄带随机过程的同向分量和正交分量。

计算机与信息工程学院综合性实验报告一、实验目的1、基于随机过程的莱斯表达式产生窄带随机过程。

2、掌握窄带随机过程的特性，包括均值（数学期望）、方差、概率密度函数、相关函数及功率谱密度等。

3、掌握窄带随机过程的分析方法。

二、实验仪器或设备1、一台计算机2、MATLAB r2013a 三、实验内容及实验原理基于随机过程的莱斯表达式00()()cos ()sin y t a t t b t t ωω=- (3.1)实验过程框图如下：理想低通滤波器如图所示：图1 理想低通滤波器()20AH ∆ω⎧ω≤⎪ω=⎨⎪⎩其它(3.2) 设白噪声的物理谱0=X G N ω（）,则系统输出的物理谱为 220=()=20Y X N AG H G ∆ω⎧0≤ω≤⎪ωωω⎨⎪⎩（）（）其它(3.3) 输出的自相关函数为:01()()cos 2Y Y R G d τωωτωπ∞=⎰ /221cos 2N A d ωωτωπ∆=⎰ (3.4) 20sin 242N A ωτωωτπ∆∆=⋅∆ 可知输出的自相关函数()Y R τ是一个振荡函数。

计算高斯白噪声x(t)、限带白噪声()a t 、()b t 及窄带随机过程()y t 的均值，并绘出随机过程各个随机过程的自相关函数，功率谱密度图形。

四、MATLAB 实验程序function random(p,R,C) %产生一个p 个点的随机过程%--------------------------高斯窄带随机过程代码--------------------------% n=1:p;w=linspace(-pi,pi,p); wn=1/2*pi*R*C;[b,a]=butter(1,wn,'low'); %产生低通滤波器Xt=randn(1,p); %产生p 个点均值为0方差为1的随机数，即高斯白噪声 at=filter(b,a,Xt); %让高斯白噪声通过低通滤波器y_at=at.*cos(w.*n); %产生随机过程a（t）y_bt=at.*sin(w.*n); %产生随机过程b（t）yt=y_at-y_bt; %产生一个p个点的高斯窄带随机过程subplot(211)plot(yt)title('高斯窄带随机过程y(t)')subplot(212)pdf_ft=ksdensity(yt) ;plot(pdf_ft)title('y(t)的概率密度图')disp('均值如下')E_Xt=mean(y_at)E_at=mean(y_at)E_bt=mean(y_bt)E_ft=mean(yt)%-----------------------自相关函数代码如下--------------------------% figure(2)R_Xt=xcorr(Xt); %高斯白噪声X(t)的自相关函数R_at=xcorr(at); %限带白噪声的自相关函数R_y_at=xcorr(y_at); %随机过程a(t).coswt的自相关函数R_y_bt=xcorr(y_bt); %随机过程b(t).coswt的自相关函数R_ft=xcorr(yt);subplot(2,2,1);plot(R_Xt);title('高斯白噪声的自相关函数R_Xt'); %并绘制图形subplot(2,2,2)plot(R_at);title('限带白噪声的自相关函数R_a_bx'); %并绘制图形subplot(2,2,3)plot(R_y_bt);title('随机过程b(t)的自相关函数R_y_bt');subplot(2,2,4)plot(R_ft);title('高斯窄带随机过程y(t)的自相关函数R_yt');%------------------------功率谱密度代码如下---------------------------% figure(3)subplot(1,2,1)periodogram(Xt);title('高斯白噪声功率谱密度S_Xt');subplot(1,2,2)periodogram(at);title('限带白噪声功率谱密度S_a_bt');figure(4)subplot(3,1,1)periodogram(y_at);title('随机过程a(t).coswt概率密度概率密度S_y_at');subplot(3,1,2)periodogram(y_bt);title('随机过程b(t).sinwt功率谱密度S_y_bt');subplot(3,1,3);periodogram(yt);title('高斯窄带随机过程y(t)的功率谱密度S_yt');五、实验结果将上述random 函数放在Path 中后，在Commaod Window 中输入：random(1000,10,0.001)时，输出结果如下：01002003004005006007008009001000-0.50.5高斯窄带随机过程y(t)0102030405060708090100246y(t)的概率密度图0500100015002000-50005001000高斯白噪声的自相关函数R X t 0500100015002000-101020限带白噪声的自相关函数R ab x 0500100015002000-50510随机过程b(t)的自相关函数R yb t 0500100015002000-101020高斯窄带随机过程y(t)的自相关函数R y t00.51-40-30-20-10010Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )高斯白噪声功率谱密度S X t 00.51-80-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )限带白噪声功率谱密度S ab t0.10.20.30.40.50.60.70.80.91-80-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )随机过程a(t).coswt 概率密度概率密度S ya t00.10.20.30.40.50.60.70.80.91-60-40-200Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )随机过程b(t).sinwt 功率谱密度S yb t0.10.20.30.40.50.60.70.80.91-50-40-30-20-10Normalized Frequency (⨯π rad/sample)P o w e r /f r e q u e n c y (d B /r a d /s a m p l e )高斯窄带随机过程y(t)的功率谱密度S y t在Commaod Window 中输出的结果如下：E_Xt = 0.0020 E_at= 0.0020 E_bt= -0.0020 E_ft = 0.0040六、实验结果分析：1、由于高斯白噪声Xt是标准正态的，所以均值趋近于零，而at，bt是由Xt通过一个线性系统（低通滤波器）得到的，所以输出均值不变，仍为零，从程序运行结果可以看出，Xt，at，bt均值都趋近于零。

实验五：窄带随机信号仿真与分析【实验目的】产生窄带随机信号，提取窄带随机信号的各个分量随机信号，测量窄带随机信号及其各个分量随机信号的参数，验证窄带随机信号及其各个低频分量随机信号的性质。

本实验安排在窄带信号课程之后来学习，使学生对窄带随机信号及其特性有个更直观和深入的了解。

【实验器材】1．设备：一台计算机2．软件：MATLAB6.5.1【实验原理】将理想白噪声 ()0n t 通过高频窄带系统可形成高频窄带噪声：()()()()()cos cos sin n t V t wt t x t wt y t wt θ=+=+⎡⎤⎣⎦(其中 w 是窄带噪声的中心频率)高频窄带噪声()n t 与其两个低频正交分量()()x t y t 、具有相同的均值和方差，两个低频正交分量()()x t y t 、具有相同的相关函数和功率谱密度；高斯窄带噪声的包络随机信号()V t 的一维分布服从瑞利分布，而其相位随机信号()t θ服从均匀分布。

【实验内容】1. 通过示波器观察高斯白噪声()0n t 的样本波形，并测量其“相关函数和功率谱、分布律”；2. 通过示波器观察高斯窄带噪声()n t 的样本波形，并测量其“相关函数和功率谱、分布律”；3. 通过示波器观察高斯窄带噪声()n t 的两个低频正交分量()()x t y t 、 的样本波形，并测量其“相关函数和功率谱、分布律”；4. 通过示波器观察高斯窄带噪声()n t 的包络随机信号()V t 和相位随机信号()t θ的样本波形，并测量其“分布律”。

注意： 本实验中窄带随机信号的形成滤波器和BPF 和()()x t y t 、的形成滤波器LPF1、LPF2的类型（Butterworth 、Chebyshev 、Elliptic 、Bessel）和参数都可设置【实验方法】先利用matlab仿真白噪声序列，然后构造一个窄带系统，使白噪声通过窄带系统形成高频窄带噪声，再提取高频窄带噪声的各个随机分量，研究高频窄带噪声和其各个低频随机分量的性质。

随机过程数学建模分析任何通信系统都有发送机和接收机，为了提高系统的可靠性，即输出信噪比，通常在接收机的输入端接有一个带通滤波器，信道内的噪声构成了一个随机过程，经过该带通滤波器之后，则变成了窄带随机过程，因此，讨论窄带随机过程的规律是重要的。

一、窄带随机过程。

一个实平稳随机过程X(t)，若它的功率谱密度具有下述性质：中心频率为ωc，带宽为△ω=2ω0，当△ω<<ωc时，就可认为满足窄带条件。

若随机过程的功率谱满足该条件则称为窄带随机过程。

若带通滤波器的传输函数满足该条件则称为窄带滤波器。

随机过程通过窄带滤波器传输之后变成窄带随机过程。

图1 为典型窄带随机过程的功率谱密度图。

若用一示波器来观测次波形，则可看到，它接近于一个正弦波，但此正弦波的幅度和相位都在缓慢地随机变化，图2所示为窄带随机过程的一个样本函数。

图1 典型窄带随机过程的功率谱密度图图2 窄带随机过程的一个样本函数二、窄带随机过程的数学表示1、用包络和相位的变化表示由窄带条件可知,窄带过程是功率谱限制在ωc附近的很窄范围内的一个随机过程,从示波器观察(或由理论上可以推知):这个过程中的一个样本函数(一个实现)的波形是一个频率为ƒc且幅度和相位都做缓慢变化的余弦波。

写成包络函数和随机相位函数的形式：X(t)=A(t)*cos[ωc t+ Φ(t)]其中:A(t)称作X(t)的包络函数; Φ(t)称作X(t)的随机相位函数。

包络随时间做缓慢变化，看起来比较直观，相位的变化，则看不出来。

2、莱斯（Rice）表示式任何一个实平稳随机过程X(t)都可以表示为：X(t)=A c(t) cosωc t-A S(t) sinωc t其中同相分量：A c(t)= X(t) cosφt= X(t) cosωc t＋sinωc t=LP[X(t) *2cosωc t]正交分量：A S(t) = X(t)sinφt=cosωc t— X(t) sinωc t= LP[-X(t) *2sinωc t]（LP[A]表示取A的低频部分）。

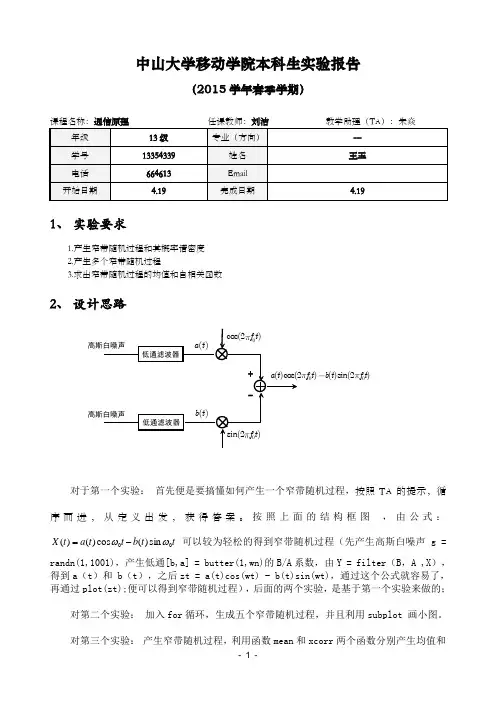
中山大学移动学院本科生实验报告（2015学年春季学期）课程名称：通信原理任课教师：刘洁 教学助理（TA ）：朱焱1、 实验要求1.产生窄带随机过程和其概率谱密度2.产生多个窄带随机过程3.求出窄带随机过程的均值和自相关函数2、 设计思路0sin(2)f t 00)()sin(2)f t b t f t对于第一个实验： 首先便是要搞懂如何产生一个窄带随机过程，按照TA 的提示，循序而进，从定义出发，获得答案。

按照上面的结构框图 ，由公式：t t b t t a t X 00sin )(cos )()(ωω-= 可以较为轻松的得到窄带随机过程（先产生高斯白噪声g =randn(1,1001)，产生低通[b,a] = butter(1,wn)的B/A 系数，由Y = filter （B ，A ,X ），得到a （t ）和 b （t ），之后zt = a(t)cos(wt) - b(t)sin(wt)，通过这个公式就容易了，再通过plot(zt);便可以得到窄带随机过程），后面的两个实验，是基于第一个实验来做的；对第二个实验： 加入for 循环，生成五个窄带随机过程，并且利用subplot 画小图。

对第三个实验： 产生窄带随机过程，利用函数mean 和xcorr 两个函数分别产生均值和自相关函数。

3、运行与测试Lab1：产生窄带随机过程和其概率谱密度在command命令框里写入：zhaidai，这是基于随机过程的莱斯表达式，产生一个1000个点的高斯窄带随机过程，和其概率谱密度（基本呈现正态分布）。

Lab2：产生多个窄带随机过程Subplot（5,2，x）让屏幕中有十个小图，分别为窄带随机过程，和其概率谱密度。

Lab3：求出窄带随机过程的均值和自相关函数分析：各个过程都是实的，中心点上相关程度最高，而且观察到：zt这个过程在中心点位置上有一个峰值，其他位置上，自相关函数会接近于零。

分析：以上是对两次窄带随机过程的均值，对于标准正态的，均值趋近于零，而at，bt是由标准正态通过一个线性系统得到的，所以输出均值不变，仍为零，从程序运行结果可以看出，均值u都趋近于零。

实验四 窄带信号的仿真和分析一、实验目的1熟悉窄带随机过程的定义，了解窄带随机过程产生的原理与方法。

2估计实验产生的窄带随机过程的功率谱。

二、实验仪器1计算机一台。

2 MATLAB 软件。

三、实验原理如果带通信号的带宽与中心频率相比非常小，即|ω2-ω1|<<ω0(或ωm<<ω0)，则称它为窄带信号或准单频信号。

222000002022()cos[()]()()()()()cos()()sin()()()cos()()sin()()cos ()()()cos ()()(;/),0n v v v n n v n v n r A r n n s t A t t v t s t n t v t i t t q t t n t i t t q t t i t A t i t q t A t q t r rA f r t e I r σωωωωωϕσσ+=+Φ=+=-=-=Φ+=Φ+⎛⎫=≥ ⎪⎝⎭只有噪声时，输出噪声幅度服从正态分布，而包络服从瑞利分布。

四 实验内容本实验模拟产生一个窄带随机过程。

首先产生两个相互独立的随机过程 Ac(t)和As(t)， 并将用两个正交载波 cos 2πf0t 和 sin 2πf0t 进行调制，如下图所示，然后进行抽样得到窄带过程的抽样。

πf 0tnTπf 0nT4.1 窄带随机过程的产生实验步骤：步骤一，理解窄带随机过程产生的框图，如图所示。

步骤二，根据所设计框图，产生两个独立的白噪声，并设计一个低通滤波器（本实验选择为）。

白噪声通过同一个低通滤波器产生两个相互独立的随机过程Ac(t)和As(t)的抽样Ac(n)和As(n)；步骤三，用两个正交载波cos2πf0nT和sin2πf0nT（T为抽样间隔，假定T=1，f0=1000/π）分别对Ac(n)和As(n)进行调制，然后通过两者相减得到窄带随机过程的抽样值；步骤四，根据计算相关函数和功率谱的数学表达式估计其值；步骤五，MATLAB编程完成上述内容。

随机信号分析实验报告——基于MATLAB语言姓名：_ 班级：_ 学号：专业：目录实验一随机序列的产生及数字特征估计2实验目的 2实验原理 2实验内容及实验结果 3实验小结 6实验二随机过程的模拟与数字特征7实验目的7实验原理7实验内容及实验结果8实验小结11实验三随机过程通过线性系统的分析12实验目的12实验原理12实验内容及实验结果13实验小结17实验四窄带随机过程的产生及其性能测试18实验目的18实验原理18实验内容及实验结果18实验小结23实验总结23实验一随机序列的产生及数字特征估计实验目的1.学习和掌握随机数的产生方法。

2.实现随机序列的数字特征估计。

实验原理1.随机数的产生随机数指的是各种不同分布随机变量的抽样序列（样本值序列）。

进行随机信号仿真分析时，需要模拟产生各种分布的随机数。

在计算机仿真时，通常利用数学方法产生随机数，这种随机数称为伪随机数。

伪随机数是按照一定的计算公式产生的，这个公式称为随机数发生器。

伪随机数本质上不是随机的，而且存在周期性，但是如果计算公式选择适当，所产生的数据看似随机的，与真正的随机数具有相近的统计特性，可以作为随机数使用。

(0,1)均匀分布随机数是最最基本、最简单的随机数。

(0,1)均匀分布指的是在[0,1]区间上的均匀分布，U(0,1)。

即实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数，通常采用的方法为线性同余法，公式如下：序列为产生的(0,1)均匀分布随机数。

定理1.1若随机变量X 具有连续分布函数，而R 为(0,1)均匀分布随机变量，则有2.MATLAB中产生随机序列的函数(1)(0,1)均匀分布的随机序列函数：rand用法：x = rand(m,n)功能：产生m×n 的均匀分布随机数矩阵。

(2)正态分布的随机序列函数：randn用法：x = randn(m,n)功能：产生m×n 的标准正态分布随机数矩阵。

随机信号分析实验报告(基于MATLAB语言)随机信号分析实验报告——基于MATLAB语言姓名： _班级： _学号：专业：目录实验一随机序列的产生及数字特征估计 .. 2 实验目的 (2)实验原理 (2)实验内容及实验结果 (3)实验小结 (6)实验二随机过程的模拟与数字特征 (7)实验目的 (7)实验原理 (7)实验内容及实验结果 (8)实验小结 (11)实验三随机过程通过线性系统的分析 (12)实验目的 (12)实验原理 (12)实验内容及实验结果 (13)实验小结 (17)实验四窄带随机过程的产生及其性能测试18 实验目的 (18)实验原理 (18)实验内容及实验结果 (18)实验小结 (23)实验总结 (23)实验一随机序列的产生及数字特征估计实验目的1.学习和掌握随机数的产生方法。

2.实现随机序列的数字特征估计。

实验原理1.随机数的产生随机数指的是各种不同分布随机变量的抽样序列（样本值序列）。

进行随机信号仿真分析时，需要模拟产生各种分布的随机数。

在计算机仿真时，通常利用数学方法产生随机数，这种随机数称为伪随机数。

伪随机数是按照一定的计算公式产生的，这个公式称为随机数发生器。

伪随机数本质上不是随机的，而且存在周期性，但是如果计算公式选择适当，所产生的数据看似随机的，与真正的随机数具有相近的统计特性，可以作为随机数使用。

(0,1)均匀分布随机数是最最基本、最简单的随机数。

(0,1)均匀分布指的是在[0,1]区间上的均匀分布， U(0,1)。

即实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数，通常采用的方法为线性同余法，公式如下：序列为产生的(0,1)均匀分布随机数。

定理 1.1 若随机变量X 具有连续分布函数，而R 为(0,1)均匀分布随机变量，则有2.M ATLAB中产生随机序列的函数(1)(0,1)均匀分布的随机序列函数：rand用法：x = rand(m,n)功能：产生m×n 的均匀分布随机数矩阵。

随机信号分析实验报告(基于MATLAB语言)随机信号分析实验报告——基于MATLAB语言姓名： _班级： _学号：专业：目录实验一随机序列的产生及数字特征估计 .. 2 实验目的 (2)实验原理 (2)实验内容及实验结果 (3)实验小结 (6)实验二随机过程的模拟与数字特征 (7)实验目的 (7)实验原理 (7)实验内容及实验结果 (8)实验小结 (11)实验三随机过程通过线性系统的分析 (12)实验目的 (12)实验原理 (12)实验内容及实验结果 (13)实验小结 (17)实验四窄带随机过程的产生及其性能测试18 实验目的 (18)实验原理 (18)实验内容及实验结果 (18)实验小结 (23)实验总结 (23)实验一随机序列的产生及数字特征估计实验目的1.学习和掌握随机数的产生方法。

2.实现随机序列的数字特征估计。

实验原理1.随机数的产生随机数指的是各种不同分布随机变量的抽样序列（样本值序列）。

进行随机信号仿真分析时，需要模拟产生各种分布的随机数。

在计算机仿真时，通常利用数学方法产生随机数，这种随机数称为伪随机数。

伪随机数是按照一定的计算公式产生的，这个公式称为随机数发生器。

伪随机数本质上不是随机的，而且存在周期性，但是如果计算公式选择适当，所产生的数据看似随机的，与真正的随机数具有相近的统计特性，可以作为随机数使用。

(0,1)均匀分布随机数是最最基本、最简单的随机数。

(0,1)均匀分布指的是在[0,1]区间上的均匀分布， U(0,1)。

即实际应用中有许多现成的随机数发生器可以用于产生(0,1)均匀分布随机数，通常采用的方法为线性同余法，公式如下：序列为产生的(0,1)均匀分布随机数。

定理 1.1 若随机变量X 具有连续分布函数，而R 为(0,1)均匀分布随机变量，则有2.M ATLAB中产生随机序列的函数(1)(0,1)均匀分布的随机序列函数：rand用法：x = rand(m,n)功能：产生m×n 的均匀分布随机数矩阵。

随机信号分析原理大作业报告专业：水声工程姓名： xxx学号：xxxxxxxxxx精选文档题目要求：给定一个白噪声信号，它的均值和方差自定。

1.设计一个线性滤波器，使该滤波器的输出为一个窄带信号。

并给出该窄带信号在不同的3个典型中心频率和带宽时的波形。

2.对该滤波器输出的上述窄带信号，用莱斯表示法对其进行建模，画出)(t a和)(t b的波形。

3.计算上述3种窄带信号对应的瞬时频率和瞬时相位，并进行包络检测。

1 窄带信号的生成 1.1 高斯白噪声的产生若)(t N 为一个具有零均值的平稳随机过程，其功率谱密度均匀分布在（-）整个频率区间，即021)(N w S n =(1) 其中，0N 为一个正实常数，则称)(t N 为白噪声。

白噪声的自相关函数为)(21)(0τδτN R N =(2) 白噪声在任意两个相邻时刻（不管这两个时刻多么的近）的取值都是不相关的，这意味着白噪声过程随时间的起伏很快，过程的功率谱极宽。

这种形式定义的白噪声只是一种理想化的模型，实际上这种白噪声是不存在的，因为按照定义，白噪声的均方值为无限大，而物理上存在的随机过程，其均方值总是有限的。

在实际工作中，当所研究的随机过程通过某一系统时，只要过程的功率谱密度在一个比系统宽大的多的频率范围内近似均匀分布，就可以把它作为白噪声来处理。

现产生一均值为0，方差为3高斯白噪声，如图1所示：式中滤波器2：中心频率f0=700Hz，带通：650～750 Hz。

滤波器2的幅度相位图以及滤波器2输出信号波形如下：图6 滤波器2输出信号的时域波形附件一滤波器1输出信号仿真程序clear allclose allclc%产生高斯白噪声N=25000; %序列长度my_var = 2;noise = sqrt(my_var)*randn(1,N);%均值为0，方差为2figure(1)plot(noise)title('均值为0方差为2的高斯白噪声')grid onfs = 25000;%采样频率f0 = 1000;%中心频率%滤波器f_pass = [900 1100];omega_pass = 2*f_pass/fs;b = fir1(192,omega_pass);figure(2)freqz(b,1,1024)%滤波器幅度和相位图像grid on%噪声通过窄带滤波器filter_outpu = filter(b,1,noise);figure(3)plot(filter_outpu)title('窄带信号在时域的波形')grid on%做fft变换Nfft = fs;fft_x = fft(filter_outpu,Nfft);ff = 0:fs/Nfft:fs-fs/Nfft;figure(4)plot(ff,20*log10(abs(fft_x)))%窄带信号的频谱title('窄带信号的频谱')xlabel('频率 Hz')ylabel('幅度 dB')grid on%窄带信号在时域的波形X_t = filter_outpu;t = 0:1/fs:1-1/fs;figure(5)plot(t,X_t)title('窄带信号在时域的波形')xlabel('t / s')grid on%莱斯表示法h_X = hilbert(X_t,Nfft) ;%希尔伯特变换omega0 = 2*pi*f0;A_t = X_t.*cos(omega0*t)+h_X.*sin(omega0*t);B_t = -1*X_t.*sin(omega0*t)+h_X.*cos(omega0*t); figure(6)subplot(2,1,1);plot(t,A_t)grid onhold onsubplot(2,1,2);plot(t,B_t)grid on%瞬时频率瞬时相位theta_t = atan(h_X./X_t);xh1=unwrap(angle(h_X));omega_t=fs*diff(xh1)/(2*pi);figure(7)plot(omega_t);title('瞬时频率')omega_t = diff(theta_t);figure(8)plot(t,theta_t)title('瞬时相位')grid on%包络检测am = abs(h_X);figure(9)plot(t,X_t,t,am,'r') %包络title('窄带信号的包络')grid on（注：可编辑下载，若有不当之处，请指正，谢谢!）精选文档。