钢梁连接节点计算

浅谈钢结构梁柱节点连接设计方法摘要：随着社会的发展与进步，重视钢结构梁柱节点连接设计方法对于现实生活具有重要的意义。

本文主要介绍钢结构梁柱节点连接设计方法的有关内容。

关键词：钢结构；节点连接；设计方法；梁柱节点；中图分类号：tu391文献标识码： a 文章编号：引言钢结构连接节点设计是钢结构整个设计工作中的一个重要的环节,连接节点的设计是否安全, 对保证钢结构的整体性和可靠度、对制造安装的质量和进度和对整个建设周期和成本都有着直接的影响。

一、钢结构梁柱节点的基本特征在钢结构设计时，对于钢结构的连接形式在计算模型中的确定是钢结构计算、设计必须首先解决的问题，其次要明确传力途径，然后才能将整个结构受力模型简化出来用软件进行分析计算。

按照传力特征不同，节点分刚接、铰接和半刚性连接。

( 1) 铰接连接节点，具有很大的柔性。

钢梁仅在腹板处采用高强螺栓连接，上、下翼缘无需进行现场焊接。

采用铰接时构造简单，使现场安装程序大为简化，现场作业量大大减小，现场安装可以不受天气及季节的影响，钢结构的安装速度大大提高。

但是，铰接连接刚度和耗能性能差，对于结构抗风、抗震不利。

( 2) 刚性连接节点，具有较高的强度和刚度。

其特点是受力性能好，但构造复杂，施工难度大。

设计中梁柱节点一般是做刚接，这是由于梁柱节点承受的荷载一般较大而且还要抵御风荷载和水平地震引起的位移。

( 3) 半刚性连接节点，刚度和强度介于铰接和刚接之间。

我国《钢结构设计规范》中没有给出半刚性连接的具体计算和设计方案，而且节点转动刚度很难确定。

这样的节点形式在工程设计中一般很少采用。

结构设计中习惯的做法是把连接当成理想刚接或者铰接，这样做能够使计算大大简化，得到的计算结果必然与实际存在偏差。

目前，主要通过采用调整系数来减少这种偏差。

二、梁柱节点的设计钢框架中梁与柱的连接起着在两种构件之间传递弯矩和剪力的作用, 是钢框架的主要组成部分, 它的性能直接关系到结构的整体反应。

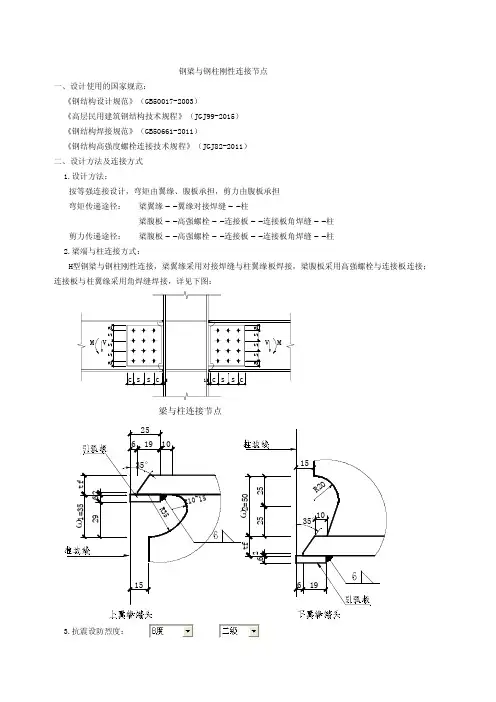
钢结构柱脚节点构造及计算钢结构柱脚节点是指钢结构柱与地基之间的连接部分。

它是整个结构体系中的关键部分，其质量和稳定性对整个结构的安全性和可靠性具有重要影响。

正确设计和施工合理的钢结构柱脚节点是确保整个钢结构工程的安全和可靠的关键。

钢结构柱脚节点的构造方法有很多种，常见的包括刚性节点、半刚性节点和柔性节点。

其中刚性节点常用于承受大荷载和地震作用的部位，半刚性节点主要用于承受中等荷载和地震作用的部位，柔性节点则多用于承受小荷载和轻型结构的构造中。

刚性节点的构造通常包括面板、剪力连接、弯矩连接和柱底板。

面板一般为钢板焊接而成，用于连接钢柱与钢梁和地基。

剪力连接通常由剪力板、螺栓和焊缝组成，用于承受柱与柱之间的剪力和水平力。

弯矩连接则通过焊接或螺栓连接柱与柱，用于承受柱与柱之间的弯矩和水平力。

柱底板是柱与地基之间的连接部分，常用于承受柱与地基之间的压力和垂直力。

半刚性节点的构造和刚性节点相似，但在节点设计时需要考虑到节点的变形能力。

常见的设计方法有节点刚度调整和节点阻尼设计。

节点刚度调整一般通过在节点处设置弹性支承或弹簧等方式来调整节点的刚度，使其能够适应结构的变形需求。

节点阻尼设计则通常通过在节点处设置阻尼器或减震器来提高节点的抗震性能，降低结构的震动响应。

柔性节点的构造相对简单，常用于轻型结构或承受小荷载的部位。

它一般由焊接连接、螺栓连接和焊接-螺栓混合连接等方式构成。

焊接连接适用于结构具有较高的刚度和稳定性的情况，螺栓连接适用于结构需要有一定的变形能力的情况，焊接-螺栓混合连接则能够综合利用焊接和螺栓连接的优点，提高结构的稳定性和可靠性。

在进行钢结构柱脚节点计算时，需考虑多个因素，包括节点的受力性能、节点的稳定性和节点的施工可行性。

受力性能的计算包括节点的切线力、切线弯矩和垂直力等受力情况的分析。

稳定性的计算包括节点的承载能力和节点的变形能力的确定。

施工可行性的计算包括节点连接的施工工艺、施工过程中的临时支撑和节点周围空间的安排等问题的考虑。

钢梁与混凝土墙铰接节点嵌固弯矩的计算方法1.引言:介绍钢梁与混凝土墙铰接节点的重要性及目的。

简要介绍相关的国内外研究现状以及存在的问题。

2.铰接节点嵌固弯矩的计算：概述节点嵌固弯矩的概念和定义。

介绍节点嵌固弯矩的计算方法，包括静力方法和有限元方法等。

详细介绍弯矩的计算公式，并给出实际应用中的具体计算实例。

3.节点嵌固弯矩的影响因素分析：分析节点嵌固弯矩的影响因素，包括钢梁、混凝土墙、连接件等的特性和参数。

详细介绍这些因素与节点嵌固弯矩之间的关系。

4.实验研究：以实验为手段，验证钢梁与混凝土墙铰接节点嵌固弯矩的计算方法和影响因素分析的正确性，并得出结论。

详细介绍实验的具体流程和结果，包括试验设计、试验装置、数据采集、分析处理等。

5.结论：对相关研究结果进行总结和归纳，阐述本文的主要贡献和创新点，同时指出存在的不足和需要进一步完善和研究的方向。

第一章引言随着城市化进程的加速，高层建筑和超高层建筑已经成为了城市建设的代表。

在这些建筑物中，钢梁和混凝土墙的结构设计与铰接节点的设置是其中一个重要的环节。

铰接节点的设计质量和施工质量，对建筑的安全性、可靠性和寿命等方面都有着至关重要的影响。

而铰接节点嵌固弯矩的计算方法和相关的影响因素分析，对于实现铰接节点的合理设计和安全评估都有着非常重要的意义。

本文将首先介绍钢梁与混凝土墙铰接节点的重要性，主要问题和目的。

然后，我们将阐述相关国内外研究现状。

最后，我们将提出钢梁与混凝土墙铰接节点嵌固弯矩计算方法、影响因素分析和实验研究。

第二章铰接节点嵌固弯矩的计算铰接节点嵌固弯矩是描述铰接节点内部点之间被嵌固的钢筋所受驱动弯矩的一个物理量。

嵌固弯矩的大小反映了铰接节点本身的承载能力和抗剪扭转的能力。

铰接节点嵌固弯矩的计算方法通常分为静力方法和有限元方法。

1. 静力方法静力方法计算铰接节点嵌固弯矩采用细致而繁琐的弹性平衡及强度理论，其本质是通过划分截面，建立静力模型进行运算得到切应力沿截面分布情况，然后依靠拉曼几何方程和梁、板单元等理论，计算节点对于各种载荷作用下的嵌固弯矩。

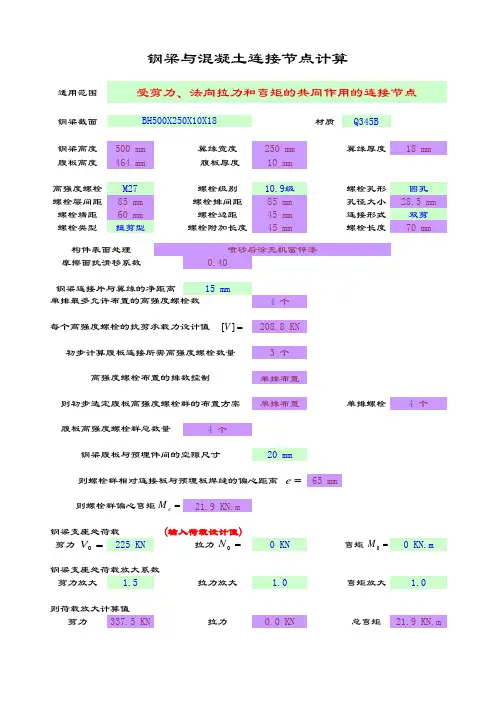
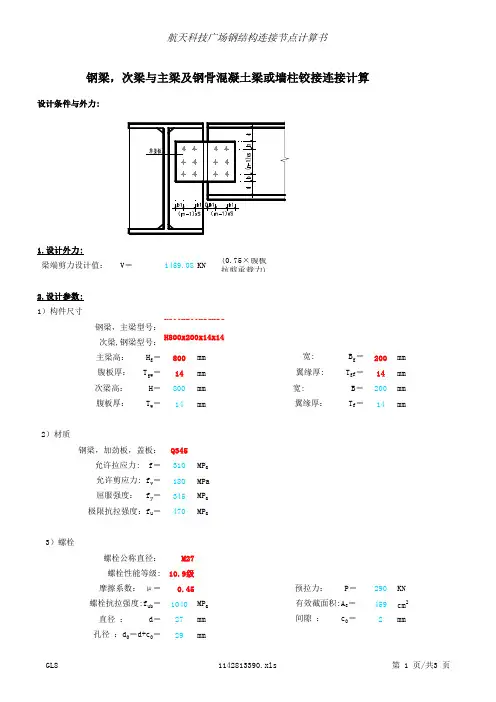
设计条件与外力:1.设计外力:梁端剪力设计值： V＝1459.08KN(0.75×腹板抗剪承载力)2.设计参数:1）构件尺寸钢梁，主梁型号： 次梁,钢梁型号： 主梁高： H g ＝800mm 200mm 腹板厚： T gw ＝14mm 14mm 次梁高： H＝800mm 200mm 腹板厚： T w ＝14mm14mm2）材质钢梁，加劲板，盖板：Q345 允许拉应力: f＝310MP a 允许剪应力: f v ＝180MPa 屈服强度： f y ＝345MP a 极限抗拉强度：f u ＝470MP a3）螺栓螺栓公称直径：M27螺栓性能等级:10.9级摩擦系数： μ＝0.45290KN 螺栓抗拉强度:f ub ＝1040MP a 459cm 2 直径 ： d＝27mm 2mm孔径 ：d 0＝d+c 0＝29mm翼缘厚： T f ＝预拉力： P＝ 有效截面积:A e ＝ 间隙 ： c 0＝钢梁，次梁与主梁及钢骨混凝土梁或墙柱铰接连接计算H800x200x14x14H800x200x14x14 宽: B g ＝ 翼缘厚: T gf ＝宽: B＝117.45KN 234.9KN 受力边边距： b＝60mm ≥58mm OK 非受力边边距:b 1＝45mm ≥43.5mm OK 孔距： s＝90mm ≥87mmOK腹板螺栓排数: n＝7 腹板螺栓列数: m＝2 腹板螺栓总数： n×m ＝144）盖板尺寸盖板至钢梁上下翼缘底边距离：56mm 盖板至钢梁上下翼56mm 盖板最小宽度：365mm 盖板宽度：365mm OK 盖板最小高度：660mm 盖板高度：660mm OK 盖板最大高度：660mmOK盖板厚度：20mm OK 60mmOK 43.75mmOK5）主梁加劲板加劲板尺寸：宽度＝93mm 高度＝772mm 厚度同次梁腹板t w ＝14mm采用双面角焊缝焊条：E50 焊缝强度: f fw ＝200MP a 取焊角尺寸 h f ＝10mm≥ 5.6mm OK ≤16.8mmOK3.构件内力设计值梁端剪力设计值： V＝1459.08KN4.设计计算:1）螺栓抗剪验算：1104.22kN0.9759焊角尺寸满足要求摩擦面数目： n f ＝单个螺栓上所承受的剪力：N v ＝V/（n×m)＝ 螺栓承载力设计值折减系数α＝（排）（列）（根）取用盖板尺寸：实际受力边边距b：实际非受力边边距b 1： 单个螺栓抗剪承载力(单剪): N v1＝0.9×μ×P＝ 单个螺栓抗剪承载力(双剪）： N v2 ＝2N v1＝＝114.62kNOK772mm 692mm150.61MP a＜200MP aOK3）盖板计算：盖板断面净面积：9720mm 2盖板剪应力：75.0556MP a ＜180MP aOK采用等面积计算:次梁，钢梁腹板开洞后净面积：8372mm 2OK焊缝长度： Ｌf ＝H g -2×T gf ＝计算长度： Ｌw ＝Ｌf －2×h f -60＝剪应力： τfv ＝V/(2×0.7×h f ×Ｌw ）＝单个螺栓的抗剪承载力设计值为：2）主梁加劲肋的连接焊缝计算：。

钢梁的长度计算规则钢梁是工业和建筑领域中常用的一种结构材料。

在钢结构设计中，精确计算钢梁长度是至关重要的。

在本文中，我们将介绍如何计算钢梁长度的规则和方法。

1. 钢梁长度的定义在结构设计中，钢梁长度指的是两个支撑节点之间的距离。

这个距离可以通过测量支撑节点之间的距离来确定，或通过计算公式来确定。

2. 计算钢梁长度的公式钢梁长度的计算公式通常是根据菲涅尔动态光学原理得出的。

菲涅尔动态光学原理是指在光线经过钢材时，由于光的折射和反射作用，使得圆锥形光束发生了扭曲。

这种扭曲是由钢材的物理特性和光线的特性共同决定的。

根据这个原理，我们可以得出计算钢梁长度的公式：L = (n+1/2)λ/√σ其中，L表示钢梁的长度，n表示菲涅尔圆纹的数量，λ表示波长，σ表示材料的弹性模量。

这个公式可以帮助工程师精确地计算钢梁的长度，以确保在实际施工中能够达到预期的效果。

3. 钢梁长度计算的注意事项在计算钢梁长度时，需要注意以下几点：（1）弹性模量：弹性模量的值取决于钢材的材质和厚度，不同的钢材和不同的厚度具有不同的弹性模量。

（2）波长：波长指的是钢材中的光线波长，通常使用红光波长。

（3）支撑节点：计算钢梁长度时，需要测量支撑节点之间的距离，确保计算结果准确。

（4）精度：在计算钢梁长度时，需要使用高精度的测量仪器和计算工具，确保结果的准确性。

4. 总结钢梁长度的计算是结构设计中至关重要的一环。

在进行钢结构设计时，需要仔细考虑材料的物理特性、计算公式和测量仪器等因素，以确保计算出的钢梁长度是准确的。

通过本文的介绍，我们相信您已经对钢梁长度计算的规则和方法有了更好的了解。