数学五年级上 封闭路线的植树问题

7 数学广角—封闭图形植树问题（教案）五年级上册数学人教版作为一名经验丰富的教师，我深知教学的重要性，因此对于每一堂课都进行了精心的设计和准备。

下面是我对于"数学广角—封闭图形植树问题"这一课的教学内容、教学目标、教学难点与重点、教具与学具准备、教学过程、板书设计、作业设计以及课后反思及拓展延伸的详细阐述。

一、教学内容本节课的教学内容选自人教版五年级上册数学教材，主要涉及“数学广角—封闭图形植树问题”。

在这一章节中，学生将学习如何在封闭图形中进行植树，以及如何计算植树的数量。

具体内容包括封闭图形的定义、封闭图形中植树的规则以及如何计算不同情况下封闭图形中植树的数量。

二、教学目标本节课的教学目标有三个：一是让学生理解封闭图形的概念，掌握封闭图形中植树的规则；二是让学生能够运用所学知识解决实际问题，提高学生的数学应用能力；三是培养学生的逻辑思维能力和团队合作能力。

三、教学难点与重点本节课的重点是让学生掌握封闭图形中植树的规则，并能够运用所学知识解决实际问题。

而教学难点则是如何让学生理解封闭图形的概念，并能够灵活运用所学知识解决不同情况下的植树问题。

四、教具与学具准备为了更好地进行教学，我准备了的教具和学具有：教材、多媒体课件、黑板、粉笔、练习题以及一些小道具，如小树苗模型等。

五、教学过程1.实践情景引入：我通过展示一些实际的植树场景，让学生了解植树的背景和意义，并引入封闭图形的概念。

2.讲解与示范：我通过讲解和示范，让学生了解封闭图形中植树的规则，并解答一些简单的例子。

3.随堂练习：我设计了几个随堂练习题，让学生运用所学知识解决实际问题，并及时给予解答和指导。

4.团队合作：我将学生分成小组，让他们共同解决一些复杂的植树问题，培养学生的团队合作能力。

六、板书设计1.封闭图形的定义：封闭图形是指由线段首尾相连围成的图形。

2.封闭图形中植树的规则：在封闭图形中，每棵树之间的间隔相等，且间隔的长度相同。

第七单元 植树问题(1)两端都种：棵数=间隔数+1(2)两端不种：棵数 = 间隔数－1(4)封闭图形:棵树 = 间隔数(3)一端种一端不种:棵数 =间隔数知识点一：两端都栽的植树问题植树问题基本解决思路：间隔数=总长÷间隔距离两端都栽：棵数=间隔数＋1知识点二：两端都不栽的植树问题两端不栽：棵数=间隔数－1知识点三：封闭图形的植树问题一端栽一端不栽：棵数=间隔数在一条首尾相接的封闭曲线上植树,所需棵数与间隔数“一一对应”,相当于线段上一端栽一端不栽的情况。

【易错典例1】在一条长300米的公路两边种树,每隔5米种一棵（两端都种）．一共种（）棵树．A．61B．121C．122【思路引导】利用植树问题公式：如果植树路线的两边与两端都植树,那么植树的棵数应比要分的段数多1,再乘2,即：棵数＝（段数+1）×2．根据植树棵数先求段数：300÷5＝60（段）,然后求植树棵数：（60+1）×2计算即可．【完整解答】解：（300÷5+1）×2＝（60+1）×2＝61×2＝122（棵）答：一共种树122棵．故选：C．【考察注意点】本题主要考查植树问题,关键是分清段数和植树棵数的关系做题．【易错典例2】（•红安县期末）一个圆形水池的周长为150米,沿池边每隔37.5米安盏观景灯,一共要安装4盏观景灯．【思路引导】根据题意,在圆形上植树,植树的棵数与间隔数相等,直接用150除以37.5即可．【完整解答】解：根据题意可得：150÷37.5＝4（盏）答：一共需要装4盏灯．故答案为：4．【考察注意点】在封闭线路上植树,棵数与间隔数相等,即：棵数＝间隔数．【易错典例3】操场上等距离放了8张课桌,把相邻的两张课桌用一段绳子连接起来,一共要准备7段绳子．【思路引导】根据题意相当于两端都不植树的问题,用课桌的张数减去1,就是一共要准备的绳子的段数．【完整解答】解：8﹣1＝7（段）答：一共要准备7段绳子．【考察注意点】如果植树线路的两端都不植树,那么植树的棵数比要分的段数少1,即：棵数＝间隔数﹣1．【易错典例4】为庆祝“六一“儿童节,学校在48米长的走廊两边摆鲜花,现在从走廊的一头开始,每隔4米摆一盆鲜花,直至走廊另一头,一共要摆多少盆鲜花？【思路引导】先看一边,据题意可知,走廊长48米,每隔4米摆一盆花,也就是48米被平均分成4米长的若干小段,花摆在分点上；所以间隔数是48÷4＝12个；又因为两端都摆花,所以盆数等于段数加1；然后再乘2就可求出两边的花盆数．【完整解答】解：（48÷4+1）×2＝13×2＝26（盆）答：一共要摆26盆鲜花．【考察注意点】此题属于植树问题．解答此类题（两端都植树）的关键要知道：植树的棵数应比要分的段数多1,即：棵数＝间隔数+1．一．选择题1．（•眉山月考）一条马路长440米,在路的两旁每隔8米植一颗树,两端都要植,共植了（）棵。

1、48名学生在操场上做游戏。

大家围成一个正方形，每边人数相等。

四个顶点都有人，每边各有几名学生？（48＋4）÷4＝13（人）答：每边各有13名学生。

2、陈庄小学有一个长60米、宽40米的小操场，四个顶点都种有一棵树，长边上每隔10米种一棵，宽边上每隔8米种一棵。

操场四周一共种树多少棵？60÷10×2＋40÷8）×2－4＝18（棵）答：操场四周一共种树18棵。

3、在一个周长为1600米的水库四周，每隔8米种一棵杨树，后来又在两颗杨树中间等距离种了两颗柳树。

问水库四周一共种了多少棵树？1600÷8×2＝400（棵）答：水库四周一共种了400棵树。

4、沿一个长50米、宽30米的长方形鱼塘每隔5米种一棵树，一共能种多少棵树？长方形周长：（50+30）×2=160（米）棵树：160÷5=32（棵）答：一共能种32棵树。

5、王大爷在正方形鱼池边上种树，每边等距种树10棵，（四个角都要种树），每辆棵之间相距4米。

鱼池的周长是多少米？（10×4－4）×4＝144（棵）答：鱼池的周长是144米。

6、圆湖的周长1350米，在湖边相隔9米种柏树一棵，在两棵柏树之间种2棵桃树，两棵桃树之间的距离是多少米？9÷（2＋1）＝3（米）答：两棵桃树之间的距离是3米。

7、在一个湖的周围每隔4米种一棵柳树,一共种了180棵。

在相邻的两棵柳树间每隔2米种一棵柏树，一共种多少棵柏树？180×（4÷2－1）＝180（棵）答：一共种180棵柏树。

8、沿着周长是240米的圆形花坛每隔6米栽一棵丁香树，再在每相邻的两株丁香树之间等距离地栽2株月季，一共能栽多少棵丁香树？一共能栽多少株月季？两棵相邻的丁香树之间的2株月季相距多少米？丁香花（封闭图形）：周长÷间距=240÷6=40（株）月季花（在丁香花的每个间隔中）：40×2=80（株）2 株月季花相距：6÷（2+1）=2（米）。

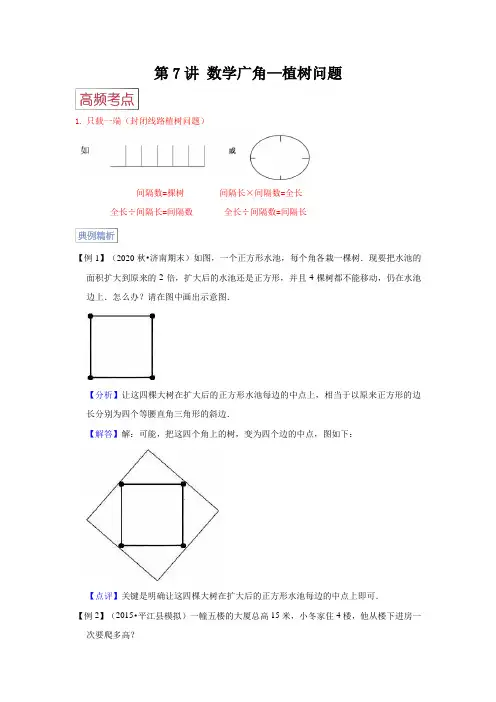
第7讲数学广角—植树问题1.只载一端（封闭线路植树问题）间隔数=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔数=间隔长【例1】（2020秋•济南期末）如图，一个正方形水池，每个角各栽一棵树．现要把水池的面积扩大到原来的2倍，扩大后的水池还是正方形，并且4棵树都不能移动，仍在水池边上．怎么办？请在图中画出示意图．【分析】让这四棵大树在扩大后的正方形水池每边的中点上，相当于以原来正方形的边长分别为四个等腰直角三角形的斜边．【解答】解：可能，把这四个角上的树，变为四个边的中点，图如下：【点评】关键是明确让这四棵大树在扩大后的正方形水池每边的中点上即可．【例2】（2015•平江县模拟）一幢五楼的大厦总高15米，小冬家住4楼，他从楼下进房一次要爬多高？【分析】五层楼总高15米，那么每层的高度是15÷5＝3米，小冬家住4楼，他从楼下进房一次要爬4﹣1＝3个楼间距，然后用3乘每层的高度即可解决问题．【解答】解：15÷5×（4﹣1）＝3×3＝9（米）答：他从楼下进房一次要爬9米高．【点评】本题属于植树问题的实际应用，关键是明确：间隔数＝层数﹣1．【例3】（2014春•杭州期末）为了保护公园里的一棵千年古树，园林局决定为它做一个圆形防护栏．如果护栏有10个间隔，一共需要打多少根木桩？【分析】根据植树的知识知道，在圆形的周围植树，间隔数就是植树的棵数，而本题中的防护栏是个圆形的，护栏有10个间隔，所以即可得出需要打木桩的根数．【解答】解：因为在圆形的防护栏周围打木桩，有几个间隔就必须打几个木桩，所以如果护栏有10个间隔，一共需要打10根木桩；答：一共需要打10根木桩．【点评】此题属于在圆形的物体周围植树的问题，即在圆形的周围植树，间隔数就是植树的棵数．2.两端都载:如图:间隔数＋1=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔长+1=棵数全长÷间隔数=间隔长全长÷（棵树－1）=间隔长【例4】（2015•平江县模拟）在一段路的路边每隔20米栽一棵树，包括这段路两端在内栽10棵树，这段路长多少米？【分析】由于从一端到另一端一共栽了10棵树，共有间隔数为：10﹣1＝9个；又由于间距是20米，根据总距离＝间距×间隔数可以求出这条路的长度，列式为：20×9＝180（米）；据此解答．【解答】解：根据分析可得，20×（10﹣1）＝20×9＝180（米）；答：这段路长180米．【点评】本题考查了植树问题，知识点是：栽树的棵数＝间隔数+1（两端都栽），总距离＝间距×间隔数．【例5】（2015春•长春校级期末）工人叔叔要在马路的一侧安装路灯，从头开始每隔4米安一个，共安装了30个，这条路长米．【分析】因为间隔数＝路灯的盏数﹣1，所以先求出马路边路灯的间隔数，再乘4即可．【解答】解：（30﹣1）×4＝29×4＝116（米）答：这条路长116米．故答案为：116．【点评】本题主要考查了间隔数＝树的棵数﹣1，再根据基本的数量关系解决问题．【例6】（2015春•务川县期中）小朋友们在路的一边植树，先植一棵树，以后每隔3米植一棵，已经植了9棵，问第一棵和第九棵树相距多少米？【分析】此题属于植树问题中的两端都要栽的情况：间隔数＝植树棵数﹣1，据此可得一共有9﹣1＝8个间隔，再乘每个间隔的长度3米，即可得出第一棵和第九棵树相距多少米．【解答】解：（9﹣1）×3，＝8×3，＝24（米）；答：第一棵和第九棵树相距24米．【点评】植树问题中：两端都要栽时，间隔数＝植树棵数﹣1．3.两端都不载如图:间隔数－1=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔数=间隔长全长÷间隔长－1=棵数全长÷（棵树＋1）=间隔长【例7】（2016春•魏县校级月考）某木工把一根长4米的圆柱形木料锯成80厘米的小段，需40分钟；如果改锯成50厘米的小段，需要多少时间？【分析】根据题意，先求出长4米的圆柱形木料锯成80厘米的小段需要锯多少次，再求出每锯一次所需要的时间，即可求出锯成50厘米的小段所需要的时间．【解答】解：4米＝400厘米，400÷80﹣1＝4（次），40÷4＝10（分钟），400÷50﹣1＝7（次），10×7＝70（分钟），答：需要70分钟．【点评】解答此题的关键是，要知道锯木料的次数比锯成的段数少1，再根据题中的数量关系即可解答．【例8】（2015春•永胜县月考）一根钢管，把它锯成7段，需要18分钟，照这样计算，如果锯成16段需要多少分钟？【分析】锯两段只需要锯1次，所以锯成7段，需要锯（7﹣1）次，用18分钟除以这个时间，就是锯一次用的时间；锯16段只需要锯16﹣1＝15次，用锯一次用的时间乘上15就是锯成9段需要的时间．【解答】解：18÷（7﹣1）＝18÷6＝3（分钟）3×（16﹣1）＝3×15＝45（分钟）答：如果锯成16段需要45分钟．【点评】本题关键是要理解锯1次就可以锯成2段，存在这个关系：锯成的段数＝锯的次数+1．【例9】（2013秋•即墨市期末）崂山举行登山大赛，组委会在长达845米的山路中，每隔65米设置一个服务站（起点和终点不设）．共设多少个服务站？【分析】先用全程除以间隔的长度，求出一共有多少段，再用段数减去1就是需要设服务站的数量．【解答】解：845÷65﹣1＝13﹣1＝12（个）答：共设12个服务站．【点评】本题属于植树问题中的两段都不栽的情况：植树的棵数＝间隔数﹣1．一．选择题（共8小题）1．（2021秋•盐都区期末）把一根电缆截成2段需要4分钟，如果截成5段需要（）分钟．A．10B．20C．162．（2020秋•黔西南州期末）一根绳子长15米，剪了三刀剪成（）段．A．3B．4C．53．（2019秋•东海县期中）大上海国际公寓步行街上两边张灯结彩，从这头到那头每隔4米挂一个红灯笼（两端都挂），步行街全长600米，一共挂了多少个红灯笼？（）A．150B．151C．302D．3004．（2021秋•巴马县期末）一根钢筋锯成6段，共需30分钟，平均锯一次需要（）分钟．A．5B．7C．6D．45．（2015秋•利川市月考）圆形滑冰场的一周全长180m．在这个滑冰场的一周每隔12m安装一盏灯，一共要安装（）盏灯．A．14B．15C．166．（2021秋•老城区期末）公园内一条林荫大道全长800米，在它的两侧从头到尾每隔20米放一个垃圾桶，一共需要（）个垃圾桶。

五年级上册数学植树问题不封闭路段两端都栽：株数=间隔数+1，总距离÷株距=间隔数不封闭路段两端都不栽：株数=间隔数-1，总距离÷株距=间隔数在封闭路段上植树时：株数等于间隔数；封闭的路线长=间隔数（株数）×株距；株距=封闭的路线长÷间隔数（株数）一、求棵树：1.有一条长800米的公路，在公路的一侧从头到尾每隔20米栽一棵杨树，需多少棵杨树苗？2.在一条长2500米的公路一侧架设电线杆，每隔50米架设一根，若公路两端都不架设，共需电线多少根？3.在一条长50米的跑道两旁，从头到尾每隔5米插一面彩旗，一共插多少面彩旗？4.两座楼房之间相距56米，每隔4米栽雪松一棵，一行能栽多少棵？二、求间距：1.红领军公园内一条林荫大道全长800米，在它的一侧从头到尾等距离地放着41个垃圾桶，每两个垃圾桶之间相距多少米？2.在一条绿荫大道的一侧从头到尾建电线杆，共用电线杆86根，这条绿荫大道全长1700米，每两根电线杆相隔多少米？三、求全长：1. 在一段公路的一边栽95棵树，两头都栽，每两棵树之间相距5米，这段公路全长多少米？2. 有320盆菊花，排成8行，每行中相邻两盆菊花之间相距1米，每行菊花长多少米？四、封闭图形1.一个圆形池塘，它的周长是300米，每隔5米栽种一棵柳树，需要树苗多少株？2.学校图书馆前摆了一个方阵花坛，这个花坛的最外层每边各摆放12盆花，最外层共摆了多少盆花？这个花坛一共要多少盆花？五、锯木头1.有一根木料，打算把每根锯成3段，每锯开一处，需要5分钟，全部据完需要多少分钟？2. 一个木工锯一根长19米的木条，他先把一头损坏部分锯下1米，然后锯了8次，锯成许多一样长的短木条，求每根短木条长多少米？六、爬楼梯和敲钟1.从一楼爬到二楼爬了几层？从一楼爬到四楼爬了几层？从一楼爬到六楼爬了几层？2.业务员小李要到六楼联系工作，他从1楼到4楼走了54级台阶，照这样计算，小李走到6楼要走多少台阶？3.挂钟6点钟敲6下，10秒敲完，那么9点钟敲9下，几秒敲完？练习：1.一个池塘周围长1800米，沿塘边每隔6米栽一棵杨树，需要种几棵杨树？2.一条走廊长21米，从走廊的一端每隔3米放一盆花，走廊的两边一共需要几盆花？3.学校两座教学楼之间的距离是40米，如果每隔5米种一棵树，共可以种多少棵树？4.在一条长为48米的马路一旁栽树，如果每4米栽一棵，一共可以栽几棵？如果一共要栽9棵，那么每两棵之间应相隔多少米？5.一幢六层楼房，每层楼有14级楼梯，小明从底楼走到六楼，共走了多少级楼梯？6.一根木料长20米，把它锯成5米长的一段，如果每据一次需要3分钟，一共需多少分钟？7.从1楼走到4楼共要走36级台阶，如果每上一层楼的台阶数都相同，那么从1楼到6楼共要走多少级台阶？8.时钟6点钟敲6下，10秒钟敲完，敲8下需要多少秒？9.一个木工锯一个长13米的木条，他先把一头损坏部分锯下1米，然后锯了5次，锯成许多一样长的短木条，求每根短木条长多少米？10.学校门口摆一排菊花，一共9盆，再在每两盆菊花中间摆3盆桂花，共摆了几盆桂花？11.一个老人在公路上散步，从第一根电线杆走到第12根用了11分，这个老人走了24分，走到第几根电线杆？12.一个圆形花圃周围长30米，沿周围每隔3米插一面红旗，每两面红旗中间插一面黄旗，花圃周围各插了多少面红旗和黄旗？13.A、B两人比赛爬楼梯，A跑到4层楼时，B恰好跑到3层楼，照这样计算，A跑到16层楼时，B跑到几层楼？14.大人上楼的速度比小孩快1倍，小孩从1楼到3楼要3分钟，那么，大人从1楼到5楼要多少分钟？15.在一块正方形地四周种树，每边都种了15棵，并且四个顶点都种有一棵树，问这个场地四周共种树多少棵？16.在一段公路的一旁栽95棵树，两头都栽，买两棵之间相距5米，这段公路长多少米？17.校园里有一段长80米的路，在路的一侧栽松树，每隔5米栽一棵，一共可以栽多少棵？18.要在100米的马路两旁植树，每隔5米种一棵，一共可以种多少棵？19.有一条公路长1000米，在公路的一侧每隔5米栽一棵垂柳，可种植多少棵？20.两座楼房之间相距56米，每隔4米栽雪松一棵，一直行能栽多少棵？21.一条长2000米的公路，在路的两边每相隔50米栽一棵白杨，从头到尾需要栽白杨多少棵？22.某大学从校门口的门柱到教学楼墙根有一条长800米的路，每边隔5米栽一棵梧桐树，需要梧桐树多少棵？23.公路的一边相隔50米有一根路灯杆，小军乘无轨电车2分钟看到马路的一边有路灯21根，电车每小时行多少千米？24.庆祝元旦，接受检阅的彩车车队共52辆，每辆车长4米，每辆车之间相隔6米，它们行驶的速度都是每分钟50米，这列火车要通过536米长的检阅场地，需要多少分钟？25.一个圆形水池周围每隔2米栽一棵柳树，共栽了40棵，水池的周长是多少？。

五上植树问题知识点
五上植树问题的知识点主要包括以下三种情况：
1. 只在一端植树（封闭线路）：在这种情况下，间隔数等于树的数量，间隔长度乘以间隔数等于整个长度。

2. 在两端都植树：这种情况下，间隔数加一等于树的数量，其他计算方式与第一种情况相同。

3. 在两端都不植树：间隔数减一等于树的数量，其他计算方式与第一种情况相同。

此外，解决植树问题的关键是理清树的数量与间隔数之间的关系。

以上信息仅供参考，如有需要，建议查阅课本或咨询数学老师。

标题：五年级上册数学教案-7 数学广角——植树问题（19）人教版一、教学目标1. 让学生理解植树问题的基本概念，掌握在封闭线路上植树的方法。

2. 培养学生运用数学知识解决实际问题的能力，提高学生的逻辑思维能力。

3. 培养学生合作学习、积极参与的精神，增强学生的集体荣誉感。

二、教学内容1. 植树问题基本概念：封闭线路、间隔、植树棵数。

2. 封闭线路上植树的方法：间隔数法、总长度法。

3. 实际应用：公园、街道、校园等地的植树问题。

三、教学重点与难点1. 教学重点：封闭线路上植树的方法。

2. 教学难点：理解间隔的概念，掌握间隔数法。

四、教学过程1. 导入新课通过展示公园、街道、校园等地的植树图片，引导学生关注植树问题，激发学生的学习兴趣。

2. 探究新知（1）让学生观察图片，找出植树问题的基本元素：封闭线路、间隔、植树棵数。

（2）引导学生思考：如何在封闭线路上植树？如何计算植树棵数？（3）介绍两种植树方法：间隔数法、总长度法。

① 间隔数法：根据间隔数和植树棵数的关系，计算出间隔长度，再计算出植树棵数。

② 总长度法：根据线路总长度和间隔长度，计算出植树棵数。

（4）通过实例演示，让学生掌握两种方法的应用。

3. 实践应用（1）给出一些实际植树问题，让学生运用所学方法解决。

（2）组织学生进行小组讨论，共同解决植树问题。

（3）引导学生关注生活中的植树问题，培养学生的应用意识。

4. 总结延伸（1）让学生回顾本节课所学内容，总结封闭线路上植树的方法。

（2）布置作业：让学生收集生活中的植树问题，下节课分享。

五、课后反思本节课通过图片导入、实例演示、小组讨论等方式，让学生掌握了封闭线路上植树的方法。

在教学过程中，要注意关注学生的学习反馈，及时调整教学方法。

同时，要注重培养学生的应用意识，让学生将所学知识运用到实际生活中。

重点关注的细节是“封闭线路上植树的方法”，这是本节课的核心内容，也是学生需要掌握的关键技能。

以下对这一细节进行详细的补充和说明。

5上－第7章－数学广角·植树问题－02基本题型－2封闭路线植树植树问题2：封闭路线植树1、封闭路线的类型。

⑴曲线图形，如圆，椭圆、半圆等。

⑵折线图形：如三角形、正方形、五角星等。

2、数量关系。

有2组数量关系。

⑴总长、间距和段数之间的关系：总长＝间距×段数段数＝总长÷间距间距＝总长÷段数⑵段数和棵数的关系。

一端植树：棵数＝段数⑶这两组关系通过“段数”相联通。

3、重要提示。

⑴曲线图形，不用考虑点上的树会重复计算。

⑵折线图形：如三角形、正方形、五角星等图形上植树，如果每个顶点都要植树。

可以这样考虑：①将点单独计算，算边上棵数时，不把点上的棵数计算在内；②每边上都有两点，将一点算在一边上，另一点算在另一边上，形成首尾相接的图形；③每边都统计点上的棵数，最后从总数中减去点数。

封闭路线植树：巩固练习1、封闭路线的类型。

⑴曲线图形，如、、等。

⑵折线图形：如、、等。

2、数量关系。

有2组数量关系。

⑴总长、间距和段数之间的关系：总长＝段数＝间距＝⑵段数和棵数的关系。

一端植树：棵数＝⑶这两组关系通过相联通。

3、重要提示。

⑴曲线图形，不用考虑点上的树会重复计算。

⑵折线图形：如三角形、正方形、五角星等图形上植树，如果每个顶点都要植树。

可以这样考虑：①将点单独计算，算边上棵数时，不把点上的棵数计算在内；②每边上都有两点，将一点算在一边上，另一点算在另一边上，形成首尾相接的图形；③每边都统计点上的棵数，最后从总数中减去点数。

知识点1、曲线图形：求总长、段长、段数、棵数。

例1-1、一个圆形水库，每隔9米种1棵柳树，共种了300棵，这个水库一周有多长？分析：这是封闭线路上植树问题，总长＝段数×段长解：9×300＝2700（米）答：这个水库一周长2700米。

例1-2、一个圆形水库一周长2700米，共种了300棵柳树，每两棵柳树之间是几米？分析：这是封闭线路上植树问题，段长＝总长÷段数解：2700÷300＝9（米）答：每两棵柳树之间是9米。