当前位置：文档之家 › 第五章 最小二乘问题分解

第五章 最小二乘问题分解

  • 格式：ppt
  • 大小：587.00 KB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

误差理论第五章最小二乘法

误差理论第五章最小二乘法
数据拟和经验公式、回归分析问题等。本章重点阐述最小二乘法原 理在线性参数和非线性参数估计中的应用
2
§5-1 最小二乘法原理
一、经典最小二乘法
为求出t个不可直接测量的未知量X 1 , X 2 , 值x1 , x2 , 量量Y 进行n次测量，得到测量数据为l1 , l2 ,
l1 Y1 f1 ( X 1 , X 2 ,, X t ) l2 Y2 f 2 ( X 1 , X 2 ,, X t ) ln Yn f n ( X 1 , X 2 ,, X t )
i 1 n
, d n的概率为： 1

1 2
n 2
e
i 2
i 1
n
(2 i 2 )
d1d 2
d n
5
根据最大或然原理，由于测量值l1 , l2 , 要使P最大，即要求：
, ln已经出现，因此
有理由认为这n个测量值出现于相应区间的概率P为最大。
12 2 2 2 2 1 2
二、等精度测量的线性参数最小二乘原理
线性参数的测量方程一般形式为： 相应的估计量为： Y1 a11 X 1 a12 X 2 a1t X t Y2 a21 X 1 a22 X 2 a2t X t Yn an1 X 1 an 2 X 2 ant X t
y1 a11 x1 a12 x2 a1t xt y2 a21 x1 a22 x2 a2t xt yn an1 x1 an 2 x2 ant xt
其误差方程式为： v1 l1 (a11 x1 a12 x2 a1t xt ) v2 l2 (a21 x1 a22 x2 a2t xt ) vn ln (an1 x1 an 2 x2 ant xt )

第五章 最小二乘法辨识

第五章 最小二乘法辨识

服从正态分
❖ 4）有效性
❖ 定理4：假设 (k) 是均值为零，方差为 2I 的正态
白噪声，则最小二乘参数估计量
^
是有效估计
量，即参数估计误差的协方差达到Cramer-Rao不
等式的下界
E (^
^
)(
)T
2E
(
T N
N
) 1
M 1
❖ 其中M为Fisher信息矩阵。
4、适应算法
❖ 随着更多观测数据的处理，递推最小二乘法对线性 定常系统的参数估计并非越来越精确，有时会发现
❖ 现举例说明最小二乘法的估计精度 ❖ 例5.1：设单输入－单输出系统的差分方程为
y(k) a1y(k 1) a2 y(k 2) b1u(k 1) b2u(k 2) (k)
❖ 设 u(k)是幅值为1的伪随机二位式序列，噪声 (k)是 一个方差 2可调的正态分布 N(0, 2 )随机序列。
❖ 为了克服数据饱和现象，可以用降低旧数据影响的 办法来修正算法。而对于时变系统，估计k时刻的 参数最好用k时刻附近的数据估计较准确。否则新 数据所带来的信息将被就数据所淹没。
❖ 几种算法：渐消记忆法，限定记忆法与振荡记忆法
❖ 矩阵求逆引理：设A为 n n 矩阵，B和C为 n m 矩阵，
并且A， A和 BCT I CT都A是1B 非奇异矩阵，则有矩
阵恒等式
A BCT 1 A1 A1B(I CT A1B)1CT A1
❖
令
A
PN1
，B
N 1
，C
T N 1
，根据引理有
PN1
T N 1 N 1
1
❖ 算法中，^ N 为2n+1个存贮单元（ai ,bi ,i 1,2, , n）， 而 PN 是 (2n 1) (2n 1)维矩阵，显然，将 N 换成 PN 后，存贮量大为减少（因为n为模型的阶数，一般 远远小于N）

矩阵论-第五章-广义逆及最小二乘

矩阵论-第五章-广义逆及最小二乘

第五章 广义逆及最小二乘解在应用上见得最频繁的、大约莫过于线性方程组了。

作一番调查或整理一批实验数据，常常归结为一个线性方程组：Ax b =然而是否是相容方程呢？倘若不是，又如何处理呢？最小二乘解是常见的一种处理方法。

其实它不过是最小二乘法的代数形式而已。

广义逆从1935年Moore 提出以后，未得响应。

据说： (S.L.Campbell ＆ C.D.Meyer.Jr Generalized Inverses of Linear Transformations 1979 P9)原因之一，可能是他给出的定义，有点晦涩。

其后，1955年Penrose 给出了现在大都采用的定义以后，对广义逆的研究起了影响，三十年来，广义逆无论在理论还是应用上都有了巨大发展，一直成为了线性代数中不可缺少的内容之一。

为了讨论的顺利进行，我们在第一节中先给出点准备，作出矩阵的奇值分解。

§5.1 矩阵的酉交分解、满秩分解和奇值分解在线行空间中，知道一个线性变换在不同基偶下的矩阵表示是相抵的或等价的。

用矩阵的语言来说，就是：若 ,m n A B C ×∈，倘有非异矩阵()P m n ×，()Q n n ×存在，使B PAQ =则称A 与B 相抵的或等价的。

利用初等变换容易证明m n A C ×∈，秩为r ，则必有P ，Q ，使000r m nI PAQ C ×⎛⎞=∈⎜⎟⎝⎠(5.1-1) 其中r I 是r 阶单位阵。

在酉空间中，上面的说法，当然也成立，如果加上P ，Q 是酉交阵的要求，情形又如何呢？下面就来讨论这个问题。

定理 5.1.1 (酉交分解) m n A C ×∈，且秩为r ，则(),(),,H H m n U m n V n n U U I V V I ∃××==，使00r HU AV Δ⎛⎞=×⎜⎟⎝⎠(m n) (5.1-2) 其中r Δ为r 阶非异下三角阵。

第五章 线性参数最小二乘法处理(1)

第五章 线性参数最小二乘法处理(1)
第五章 线性参数的最小二乘法处理
光电效应
1 E = hν = m υ0 2 + A 2
1 eU 0 = m υ0 2 2
h A U0 = ν e e
2
光电效应
频率νi(×1014Hz) 8.214 7.408 6.879 5.490 5.196 截止电压U0i(V) 1.790 1.436 1.242 0.688 0.560
3
光电效应
SLOPE函数
频率ν i(Hz) 8.214E+14 7.408E+14 6.879E+14 5.490E+14 5.196E+14 截止电压U0i(V) 1.790E+00 1.436E+00 1.242E+00 6.880E-01 5.600E-01
4.02964E-15
2.000E+00 1.800E+00 1.600E+00
1
i 2
e
i 2 ( 2 i 2 )
di
( i 1, 2,
, n)
由概率论可知，各测量数据同时出现在相应区域的概率
为ቤተ መጻሕፍቲ ባይዱ
P Pi
i 1
n
1

1 2 n
2
e n

i 1
n
i 2 (2 i 2 )
d 1d 2
d n
12
第一节 最小二乘原理
1.400E+00
y = 4E-15x - 1.5314
1.200E+00 1.000E+00 8.000E-01 6.000E-01
4.000E-01
2.000E-01 0.000E+00 0.000E+00 5.000E+14 1.000E+15

电力系统自动化5 电力系统最小二乘法状态估计

电力系统自动化5 电力系统最小二乘法状态估计
x x1
；
X 1 ( H R H ) H R [ Z h( X 1 )]
T -1 v T -1 v
1
iii. 求
x1
iii. 求 X 1 ； iv. 第一次迭代结果
( x) ( x )
x x1
；
v. 重复ii ~ iv，直到获得较满意的 X 。
线性方程组的计算机解法之一 ——平方根因子分解法（略）
X 2 X1 X1
iv. 第一次迭代结果
x 2 x1 x1
v. 重复ii ~ iv，直到获得 较满意的 x。
第五章 电力系统运行的状态估计
第四节 电力系统最小二乘法状态估计
最小二乘法状态估计程序框图（图5-12） 例：图5-13，5-14，表5-4~5-7
Y13 Y31 y13 YT k 1 1 1.05 j7.5 j0.1269
T
T
电力系统中，Z 的元素包括状态变量的测量读值 Z X 和其他 系统变量的测量读值 Z Z 。
Z Z X
ZZ
Z Z 为 X 的非线性函数，故电力系统的量测方程式为
Z = h (X) + V
第五章 电力系统运行的状态估计
第四节 电力系统最小二乘法状态估计
注意：i. m n Z ii. 相角一般不能直接测量（*PMU）， Z 维数高于 Z X 。
故
H 12
P U
0,
H 21
Q θ
0
H 11 H (θ, U) 0
再经一些近似，可得
H 11 H (θ, U) 0
0 H 22
0 U 02 H 1 H 22 0

第五章线性参数的最小二乘法处理01

第五章线性参数的最小二乘法处理01

第五章线性函数的最小二乘处理最小二乘原理应用时的条件是：函数关系确定已知、等精度、误差独立、无偏估计得到满足，在众多的N个测量方程中利用最小二乘原理求得t个（t＜／N）参数的最佳估计值。

如前所叙，在随机因素作用下，测量次数较多时，计算的结果就会更精密，测量次数往往大于待求未知量的个数，因而出现N＞t的现象就成为自然而然的事情了。

众所周知，当N＝t时可由线性代数知识求得一组唯一正确解。

当N＞t时，代数解法则无能为力了。

也许读者会提出另外一个问题：既然N＞t，可由N中取出t个方程来求解，而把（N-t）个方程弃掉，问题不就解决了吗？答案是不行的。

这样求解后的结果不是最佳值，有时会与最佳值离歧很大。

最小二乘法是一种数学原理，高斯于1809年在他的名著《天体沿圆锥截面绕太阳运动的理论》一书中，发表了他发现的最小二乘原理并应用于测量之后，在许多科学领域及技术领域中得到越来越多地应用。

5.1 函数为直接测量值得线性组合5.1.1 测量方程式函数中可能存在着多个待定参数，根据该函数关系可列出多个测量后的方程式，该方程式称作测量方程式。

设含有t个待求参数Xj(j=1,2,…,t)的函数关系已知，表现为线性组合，即Xj是待定系数的真值，aj是在某具体测量条件下获得的直接测量值，经N次测量（N>t）后，理应得到N个函数真关系式。

为了表达更简洁，可将各方程中系数用aij(i=1,2, …,N;j=1,2, …,t)表示，上述方程可简写成量值Y经N次测量后的测量值用Mi表示，则上述方程变为测量方程式，又称测量条件方程，式中，aij及Mi是在某具体测量条件下的直接测量值，Mi含有误差，即Mi≠Yi。

5.1.2 剩余误差方程式若用同直接测量时一样，可将称作剩余误差。

由此便可得到N个剩余误差方程式可以看出，剩余误差是各最可信赖值的函数，即5.1.3 正规方程组现在以三个待求量x1,x2,x3为例，说明建立正规方程组的过程，该计算方法和过程及结论，可推广到t个待求量中去。

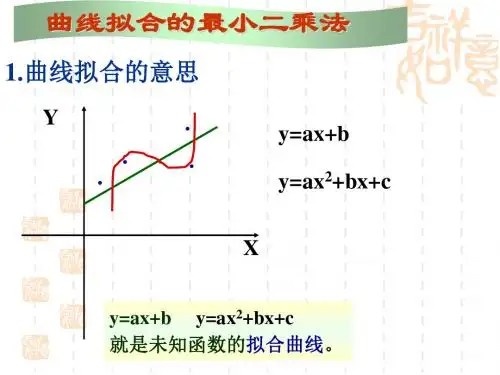
第5章-1 曲线拟合(线性最小二乘法)讲解

第5章-1 曲线拟合(线性最小二乘法)讲解
a ∑xi2 +b ∑xi= ∑xi yi a ∑xi+bn=∑ yi
求所需系数，得到方程： 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得：
a=0.912605
b=0.174034
所以线性拟合曲线函数为： y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数： y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
曲线拟合的最小二乘法
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为： y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62

最小二乘的解

最小二乘的解

最小二乘的解
最小二乘法是一种常见的数学方法，用于解决线性回归问题。

它的基本思想是通过求解最小化误差平方和的问题，找到最接近观测数据的数学模型。

在最小二乘法中，我们首先需要有一组观测数据，通常表示为一系列的点。

我们假设这些观测数据可以由一个线性模型表示，该模型可以用一条直线的方程来描述。

我们的目标是找到一条直线，使得观测数据点到这条直线的距离之和最小。

为了达到这个目标，我们先定义一个误差函数，它是观测数据点到直线的距离的平方和。

然后我们通过对误差函数求导，将问题转化为求解一个线性方程组的问题。

最终，我们可以得到一组系数，这些系数可以用来表示最佳拟合直线的方程。

最小二乘法在实际问题中有着广泛的应用。

例如，在经济学中，我们可以使用最小二乘法来分析需求和供应关系。

在物理学中，最小
二乘法可以用来拟合实验数据，从而找到实验结果的数学模型。

在工程学中，最小二乘法可以用来解决信号处理和图像处理的问题。

总而言之，最小二乘法是一种强大的数学工具，用于解决线性回归问题。

通过最小化观测数据与数学模型之间的误差平方和，我们可以找到最佳拟合模型的系数。

这种方法在实际应用中具有重要的意义，并且被广泛应用于各个领域。

(完整版)5线性参数的最小二乘法处理(精)

(完整版)5线性参数的最小二乘法处理(精)

一、等精度测量线性参数的LSM处理的正规方 程。
❖ 线性参数的误差方程式为：
l1 a11x1 a12 x2 ... a1t xt v1
l2 a21x1 a22 x2 ... a2t xt v2
……
ln an1x1 an2 x2 ... ant xt vn
v2
第三节 精度估计
❖ 一、测量数据的精度估计
❖ （一）等精度测量数据的精度估计
❖ 对包含t个未知数的线性参数方程，进行n次独立的 等精度测量。
❖ 可以证明
❖
[V V ] ~ 2 n t
2
E[V V
2
]
n
t
❖取
s 2 v v
nt
s
v
2 i
nt
❖ V1=3-(1.28×1+0.418×2)=0.884 ❖ V2=5-(1.28×1+0.418×10)=-0.46 ❖ V3=8-(1.28×1+0.418×20)=-1.64 ❖ V4=15-(1.28×1+0.418×30)=1.18 ❖ V5=18-(1.28×1+0.418×40)=0
L
8
15
18
AT A 1052 3100024 AT L 134698
( AT
A)1
1 4616
3004 102
1502
X
( AT A)1 AT L
1 4616
3004 102
1502134698 01..42188
❖ 正规方程为： ❖ 5x+102y=49 ❖ 102x+3004y=1386 ❖ 解该方程得到 ❖ x=1.28 ❖ y=0.418
i

最小二乘法超详细推导

最小二乘法超详细推导

最小二乘法超详细推导好，咱们聊聊最小二乘法，听起来是不是有点儿高大上？但其实它的原理就像是在生活中解决问题一样简单。

想象一下，你跟朋友约好一起去看电影，结果两个人的时间都不太对付，最后迟到了。

为了避免下次再犯错，你们想出一个办法：每次都提前半小时出门。

这就像最小二乘法，简单明了，追求一个更好的结果。

最小二乘法的基本思想就像是给一堆点点画线，想要找到一条“最佳”线，让这条线跟所有的点距离最小。

听上去有点抽象，但我给你举个例子。

假设你正在学习滑板，刚开始的时候，可能会摔得东倒西歪，根本控制不住。

你想要找出一个滑行的规律，比如，哪个角度、哪个姿势滑起来更顺畅。

于是你反复尝试，记录每次摔倒的位置，然后把所有这些点连起来，最后找到那个“最佳姿势”。

这就像是在求一个最小值，把每次摔倒的距离都尽量缩短。

让我们深入一点儿，最小二乘法的数学公式其实挺简单，咱们用y=ax+b来表示。

这里的y就像你想要达到的目标，比如说滑板的速度，x是你能控制的因素，比如滑板的角度。

a是斜率，代表你加速的程度，b则是你起步的高度。

听上去是不是有点像在调配一杯完美的饮料？如果把这几个变量调得刚刚好，恰到好处，那就能滑得又快又稳。

这时候，我们就要把所有的点放到图上，看看哪个点偏离得最多。

每个点到那条线的距离就像是你在追求完美的过程中产生的小失误。

咱们要做的，就是把这些距离的平方加起来，然后最小化，尽量让整体的偏差小到可忽略不计。

这个过程就像在追求一个完美的曲线，让你在滑板上飞翔的时候不再摔倒。

在实际操作中，我们往往需要用到一些数学工具，比如微积分。

听起来是不是有点吓人？别担心，其实就是为了找出那条最佳线的斜率和截距。

简单来说，就是要把所有的偏差搞清楚，给出一个准确的答案。

就像你在追求更好的生活方式，每天记录饮食和运动，最后找到那个最适合自己的节奏。

想象一下，咱们在找线的时候，就像在追寻自己的梦想。

每一次失败，每一次尝试，都是为了一条更完美的路径。

最小二乘法原理的几何解释

最小二乘法原理的几何解释

(2)
a1 a2
得到(3)式。
从列的方向看矩阵， 可以看到 a1 a2 b 三个列向量， 这样看还不是很明显， 干脆把(2)式再拆开，
Macer
MCR
1 1 3 -1 x1 1 x2 1 a1 x1 a2 x2 b
一但化成列的形式，我们就很自然想到把向量 a1 a2和b 画到图上。
Macer
MCR4Βιβλιοθήκη ba1a2
图 4
要找到解，就要找到 a1和 a2 的一个线性组合，使得组合后的向量刚好等于 b 。可惜的是任何的 只可能出现在 a1和 a2 所在的平面 S 上 （这个平面 S 就是传说中的向量空间） ， a1和 a2 线性组合， 但是向量 b 不在平面 S 上，如图 5。不可能找到解，怎么办呢？
4
3
y = 0.5x + 1.8333
2
1
0
0
1
图 8
2
3
Macer
MCR
7
图 8 既不是行的角度， 也不是列的角度， 它只是问题的来源， 那如果从行的角度看方程(4)， 是什么样子的，方程的每一行都是一条直线，三条直线不相交于一点，我们的解是图 9 中的 圆点，是中间三角形的重心？质心？不知道呀看起来有点像。
AT e 0
(6)
ˆ AT b ，这就是传说的超 ˆ 0 ，化简一下就是 AT Ax 把(5)带入(6)中，结果出来了， AT b Ax
ˆ AT A AT b 。 定方程的解法，这么简单就推出来了！所以最佳的近似解就是 x
1
这里你是否担心 AT A 不可逆？不会的， 只要 A 的每一列是线性无关的， 那么 AT A 就是一个可逆 的对称的方阵。这样，按公式解出的

第五章线性参数的最小二乘法处理

第五章线性参数的最小二乘法处理
第5章 线性参数的最小二乘法
5-1
最小二乘法（least square method）
1805年，勒让德（Legendre）应用“最小二乘法”， 确定了慧星的轨道和地球子午线段。 1809年，高斯（Gauss）论证其解的最佳性。
经典最小二乘法（即代数最小二乘法）
现代最小二乘法（即矩阵最小二乘法）
(n=t)
正规方程：误差方程按最小二乘法原理转化得到的 有确定解的代数方程组。
5-18
第二节、正规方程
一、等精度测量线性参数最小二乘法的正规方程 二、不等精度测量线性参数最小二乘法的正规方程 三、非线性参数最小二乘法处理的正规方程（略） 四二节
正规方程
一、等精度测量线性参数最小二乘处理的正规方程
误差方程
a11 , a12 , , a1t a , a ,, a 2t A 21 22 a n1 , a n 2 , , a nt
系数矩阵
误差方程
v1 l1 (a11 x1 a12 x 2 a1t xt ) v 2 l 2 (a 21 x1 a 22 x 2 a 2t xt ) v n l n (a n1 x1 a n 2 x 2 a nt xt )
相应的估计值
y1 a11 x1 a12 x 2 a1t xt y 2 a 21 x1 a 22 x 2 a 2t xt y n a n1 x1 a n 2 x 2 a nt xt
其误差方程：
v1 l1 (a11 x1 a12 x 2 a1t xt ) v 2 l 2 (a 21 x1 a 22 x 2 a 2t xt ) v n l n (a n1 x1 a n 2 x 2 a nt xt )

最小二乘问题的解法

最小二乘问题的解法
的线性组合考虑个已经函数上取值的并假定给出在定义残量为此能最佳地逼近数据估计参数则问题转化为量形式则残量可表示为下列向和向量若用引入矩阵问题简记为该问题称为最小二乘问使得确定及向量给定矩阵定义squaresleastlsayaxth的解存在的充分必要条方程组定理得证即有于是这里充分性必有由此即知这说明即有的列向量的线性组合设存在必要性axth是其任一给并且假定的解存在方程组如果反之于是有满足方程组如果axazaxayaxth的充要条件是解唯一而且其是存在的的最小二乘问题的解总线性方程组axax的充分必要条件是因此注意到达到最小达到最小当且仅当故此从而正交于是对任意其中可以唯一地表示为所以向量要条件是的最小二乘解的充分必那么其中注意到于是那么的最小二解正则化算法正则化算法的基本步骤如下
Hx
x
u
w
proof
(1)显然成立， ( 2)和(3)可直接得出， 事实上 H T H H 2 ( I 2 ww T )( I 2 ww T ) I 4 ww T 4 ww T ww T I
2
w
令w ( x y ) / x y 2 , 构 造Householde r变 换 2 H I 2 ww T I ( x y )( x y ) T 2 x y 2 注意到 x T x y T y (已 知),于 是 2 x y 2 ( x y ) T ( x y ) 2( x T x y T x ) 2 ( x y ) T x 从而 2 Hx x ( x y )( x y ) T x x ( x y ) y 2 x y 2 proof
i 1 T n
这 里A a i ,, a n .
于 是, 令x ( x1 , , x n ) ,即 有Ax b. 定理得证 Th3.1.2 方程 组 Ax b的解 存在 , 并且 假定 x是其 任一 给 定的 解 , 则方 程组 的全 部解 的集 合是 x N ( A) proof : 如 果y满 足 方 程 组 , 则A( y x ) 0,即( y x ) N ( A), 于是有 y x ( y x ) x N ( A).反 之, 如 果y x N ( A),则 存 在z N ( A),使y x z, 从 而 有 Ay Ax Az Ax b. 证 毕.

(完整版)5线性参数的最小二乘法处理(精)

(完整版)5线性参数的最小二乘法处理(精)

一、等精度测量线性参数的LSM处理的正规方 程。
❖ 线性参数的误差方程式为：
l1 a11x1 a12 x2 ... a1t xt v1
l2 a21x1 a22 x2 ... a2t xt v2
……
ln an1x1 an2 x2 ... ant xt vn
v2
AT L A X 0
( AT A) X AT L
❖ 解上面方程组得
X AT A 1 AT L Nhomakorabea❖ 可以证明最小二乘估计值是无偏估计。
❖ 测量方程为：
❖
x+2y=3
❖
x+10y=5
❖
x+20y=8
❖
x+30y=15
❖
x+40y=18
1 2
1 10
A 1
20
1 30
1
40
3 5
ank [ln (an1 x1 an2 x2 ... ant xt )] 0 k 1,2, ,t
记
[ai ai ] a1i a1i a2i a2i ... ani ani i 1,2 ,t [ai a j ] a1i a1 j a2i a2 j ani anj (i, j 1,2, ,t) [ai L] a1il1 a2il2 ... aniln i 1,2 ,t
' i
.........
i
L* A* X V *
最小 ❖
V *V
(L*
A*
^
X )T(L*
A*
^
X)
第二节 正规方程
❖ 为了得到可靠的测量结果，测量次数n总是要 多于未知数的数目t。因而直接用一般解代数 方程的方法求解这些未知数是不可能的。最 小二乘法可以将误差方程转化为有确定解的 代数方程，而且方程个数正好等于未知数的 个数，从而可求解这些未知数。

第5章最小二乘法

第5章最小二乘法
(2)解是观测值的线性组合，且有最小方差。这称为高 斯—马尔可夫定理; (3) 加权的残差平方和的期望值是
当σ2＝1，即取wi＝1/σi2，这时称 为χ2 量。期望值为n－k。
第5章最小二乘法
第二节 线性参数的最小二乘法
一般情况下，最小二乘法可以用于线性参数 的处理，也可用于非线性参数的处理。由于测 量的实际问题中大量的是属于线性的，而非线 性参数借助于级数展开的方法可以在某一区域 近似地化成线性的形式。
这里y0i表示xi对于的Y的变量真值，△i表示相应的测量 误差。
假设诸观测值相互独立且服从正态分布。在等精度观测的 情况下，即认为各误差服从相同的正态分布N(0， σy)。
现在的问题是一个参数估计问题：需要给出a1，a2，…， ak的估计值 ， aˆ1 aˆ 2 ，…，aˆ k 。
解决这类问题最常用的方法就是最小二乘法。在一些情况 下，即使函数值不是随机变量，最小二乘法也可使用。
选取的参数估值应使诸观测值yi与其估计值 yˆ i 之差的加 权平方和为最小。用式子表示就是要使
=最小 其中，wi为各观测值yi的权。wi＝σ2／σi2，，i＝1， 2，…，n。这里σ2为任选的正常数，它表示单位权 方差。
第5章最小二乘法
不等精度情况下的最小二乘法正规方程
同样地，根据数学分析中求函数极值的条件：
第5章 线性参数的最小二乘法处理
最小二乘法是用于数据处理和误差估 计中的一个很得力的数学工具。对于从 事精密科学实验的人们说来，应用最小 二乘法来解决一些实际问题，仍是目前
必不可少的手段。
第5章最小二乘法
第一节 最小二乘法原理
• 最小二乘法的发展已经历了200多年的历史， 它最早起源于天文和大地测量的需要，其后 在许多科学领域里获得了广泛应用。特别是 近代矩阵理论与电子计算机相结合。使最小 二乘法不断地发展而久盛不衰。

广义最小二乘法

广义最小二乘法

广义最小二乘法第五章广义最小二乘法当计量经济学模型同时存在序列相关和异方差,而且随机误差项的方差-协方差矩阵未知时我们可以考虑使用广义最小二乘法(gls)。

即下列模型：y=xβ+μ满足这样一些条件：e(μ)=0cov(μμ')=δ2ωω=11ω1221ω221ωn2...ω1n...ω2nωnn设立ω=dd'用d左乘y=xβ+μ的两边，得到一个新的模型d-1y=d-1xβ+d-1μy=x**-1β+μ*（1）该模型具备同方差性和随机误差相互独立性。

因为可以证明：e(μ*μ*')=δ2i于是需用普通最轻二乘法估算（1）式，获得的参数估计结果为ˆ=(x*'x*)-1x*'y*β=(x'ωx)x'ωy整个过程最重要的一步就是要估计ω，当模型存在一阶自相关时。

我们取-1-1-1ρn-1ρn-2ρn-1ρn-21案例四：广义最小二乘法在这里我们举例子去表明广义最轻二乘法的应用领域。

在探讨这个问题时所使用的数据如下表中5.1右图：首先我们计算ρ，我们可以直接根据ols估计出来的dw来计算，ols估计出来的结果为下表5.2：可以根据ρ=1-dw/2，dw=0.8774，因此ρ=0.5613,在这个基础上,我们可以得出结论这个方差-协方差矩阵。

方差协方差矩阵可以由以下一个程序去赢得：!p=0.5613matrix(17,17)fac1for!i=1to17fac1(!i,!i)=1for!j=1to17for!i=!j+1to17fac1(!i,!j)=!p^(!i-!j)fac1(!j,!i)=fac1(!i,!j)得到的矩阵结果为下表5.3下面再展开cholosky水解,获得d,展开cholosky水解时所用至的命令如下:1sym(17,17)fact1matrixfact1=@cholesky(fact)得到的fact1矩阵如下解fact1的逆矩阵就可以将数据展开切换,获得m2和gdp,解逆矩阵时使用的命令如下:matrix(17,17)fact2**fact2=@inverse(fact)得到的fact1矩阵的逆矩阵fact2如下m2*=m2*fact2gdp*=gdp*fact这样就可以获得一组转换后的数据,数据如下再对这组数据进行普通最小二乘法就可以得到这个方程的广义最小二乘法的估计结果,结果如下:可以看见，采用广义最轻二乘法后，序列有关的情况获得提升。

最小二乘法

最小二乘法

(1)正交性的有关性质
在线性代数欧氏空间理论中 , 将 R 3 中两个向量 x,y之间的夹角φ满足的关系式 xTy=‖x‖2‖y‖2cosφ 推广到Rn. T
x y 1 设x,y∈Rn, 由Cauchy不等式 1 || x ||2 || y ||2
从而得到Rn中两个向量之间的夹角为
x y arccos || x ||2 || y ||2
(i , f ) ( xk )i ( xk ) f ( xk )
k 0
m
则:
(i , f ) ci (i ,i )
拟合函数 f ( x) c00 ( x ) c11 ( x ) cnn ( x)
例1
设函数y=f(x)的离散数据如下表所示, 试用二次 多项式拟和上述数据,并求平方误差. i 0 xi 0 yi 1.000 1 2 3 4 5 0.2 0.4 0.6 0.8 1 1.221 1.492 1.822 2.226 2.718
T
定理1
设x, y是Rn中的向量, x与y正交的充分必要条
件为xＴy=0.
证明 必要性. 当x与y正交，它们的夹角φ=π/2， 有xＴy=0. 充分性. 当xＴy=0, φ=π/2, 即x与y正交. 注：如果x与y正交, 记为x⊥y
定理2
设x, y∈Rn, 且x⊥y, 那 么： ‖x+y‖22＝‖x‖22＋‖y‖22．
假设x⊥R(A), 即αiＴx=0 (i=1,2,…,k). 从而AＴx=0 另一方面,如果AＴx=0, 那么有z∈Rk, 使Az=y∈R(A). 这时，yＴx=zＴAＴx=0,即x⊥y. 由z的任意性， 得Az是任意的， 因此x⊥R(A). 由这个定理， 容易得到： 推论1 设A是n×k阶矩阵， 那么R(A)有唯一的正交 补子空间N(AＴ).

第五章--最小二乘问题的解法 (1)

第五章--最小二乘问题的解法 (1)

第五章 最小二乘问题的解法1.最小二乘问题 1)回归方程问题[]Ti i l i y t t)()()(1,,...,,m i ,...,2,1=是m 个实验点。

现要根据这些点确定y 与l 个物理量l t t t ,...,,21之间的关系式。

设这种关系式为),...,,,...,(11n l x x t t F y =，其中n x x ,...,1是方程中需要待定的n 个参数(系数)。

因此问题是如何通过)(n m m >个实验点，确定方程中的系数。

由于实验点的个数大于待定系数的个数，因此方程中系数的确定是一个超静定问题，无法按一般的方法进行求解。

此时将实验点到曲面距离最短的那个曲面作为所求曲面，从而求取该曲面方程。

即求解[]∑=-mi i i y x t F 12)()(),(min ，这就是最小二乘问题。

2)非线性方程组问题求解非线性方程组⎪⎪⎩⎪⎪⎨⎧===0),...,(............................0),...,(0),...,(11211n n nn x x f x x f x x f 可转化为求解如下形式的最小二乘问题。

∑=mi n i x x f112),...,(min显而易见，最小二乘法的一般形式可写为)()(min x f x f T最小二乘法问题实际上是具有n 个变量的无约束极小化问题，前面解无约束优化问题的方法均可应用。

但是最小二乘问题具有一定的特殊性，即目标函数的表达式是由多个表达式的平方和组成，理应有更、更有效的方法。

这正是最小二乘解法要解决的问题。

2.线性最小二乘问题的解法最小二乘法的一般形式可写为)()(min x f x f T特别地，当b Ax x f -=)(，即)(x f 为线性函数时，则最小二乘问题可表示为：2min b Ax -1) 线性最小二乘问题解的条件定理1:*x 是线性最小二乘问题极小点的充要条件是*x 满足b A Ax A T T =。

第五章参数的最小二乘法估计

第五章参数的最小二乘法估计
a 式中， j ， y 分别为如下列向量
第二节 线性参数的最小二乘法
a1 j a2 j aj a nj
y1 y2 y y n
第二节 线性参数的最小二乘法
[al ak ] 和 [a j y ]分别为如下两列向量的内积：
如为精密测定1号、2号和3号电容器的电容量
x1 x2 x3
待求量 测得值
为了获得更可靠 的结果，测量次 数总要多于未知 参数的数目
y1
y3 y2
0.3 ( y1 )
y4
待解的数学模型
x1 x2 x1
0.4 ( y2 )
x3 0.5 ( y3 ) x2 x3 0.3 ( y4 )
• （1）最小绝对残差和法： • （2）最小最大残差法： • （3）最小广义极差法：
v
i
Min
max vi Min
maxvi minvi Min
主要内容
• 最小二乘法原理 • 线性测量方程组中参数的最小 二乘法 • 非线性测量方程组中参数的最 小二乘法 • 组合测量
第二节 线性参数的最小二乘法
v1 v2 V vn
l1 l2 L= ln
和n×t阶矩阵
第二节 线性参数的最小二乘法
a11a12 a1t A a21a22 a2t a a a nt n1 n 2
第二节 线性参数的最小二乘法
测量方程组系数与正规方程组系数
y1 a11 x1 a12 x2 a1t xt y2 a21 x1 a22 x2 a2t xt yn an1 x1 an 2 x2 ant xt
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

充分性：设 x * 满足（ 7）即：AT ( AX * - b) 0 对任意向量V X * Z R n .计算 AV - b
* 2
A( X Z ) - b
* 2
2
AX - b AX - b
*
AZ AZ
2
2 Z T AT ( AX * - b) 0
2
2 2
f1 x1 , x2 , xn 0 f x , x , x 0 2 1 2 n f m x1 , x2 , xn 0
min f i 2 x1 , x2 , xn
i 1
m
（3）是有n个变量的无约束极小化问题，一般可 以用前面介绍的最优化方法求解。考虑到（3）的特 殊形式，可以考虑更有效、更简单的方法求解。 f 的Jacobi矩阵：
即[ AT ( xk ) A( xk ) S ( xk )]Pk AT ( xk ) f ( xk ) X k 1 X k Pk
主要计算量是 Sk 的计算，尽管Sk对称，也包含 (1/2)mn(n+1)个二阶偏导数，但Hesse矩阵中第一项只含 一阶导数的信息。因此为简化计算，我们或者忽略Sk， 或者用一阶导数的信息逼近Sk。 由（4）可知，当 2 fi ( x) 接近0或 fi(x)接近线性从而 接 近于0，此时才可以忽略 Sk，因此这类算法又称为最小余 量算法。 而称逼近Sk的一类算法为大余量算法。
f1 x 1 f 2 x1 A f ( x ) f m x1 f1 f1 x2 xn f 2 f 2 x2 xn f m f m x2 xn
若 则
n
yR
m
t , t t
(i ) 1 (i ) 2

(i ) T l

R l i=1~m
fi ( x) F (t (i ) , x) y(i) ,
i=1~m.
f ( x) ( f1 ( x), f m ( x))T Rm
则上面问题可记为:min f(x)Tf(x) (3) (3) 即为最小二乘法问题一般形式。 当f(x)为线性向量值函数时，称（3）为线性最小 二乘法问题。 否则，原问题称为非线性最小二乘法问题。
第五章 最小二乘问题
5.1 引言
在数字处理中经常遇到寻求回归方程的问题，即根据一 组实验数据建立两个或多个物理量（俗称因素）之间的在 统计意义上的依赖关系式。 这类问题的数学模型如下： 设物理量 y 与物理量 t1,t2,…tl 之间的依赖关系式，设 其方程为： y=F(t1,…tl,x1…xn) (1) 其中 x1…xn为待定参数。我们的问题是如何通过m(>n) 个实验点 [t1(i) ,t2(i) ,…tl(i), y(i)]T i=1,2…m 确定（1）中n个 参数x1,x2…xn.从而建立回归方程。
5.2 线性最小二乘法问题的解法
当f(x)取线性形式 即f(x)=Ax-b.A是m×n矩阵， b Rm 则（3）为：min||Ax-b||2
(m<n) (6)
定理1 x*是（6）的极小点的充要条件是x*满足向量组： ATAx*=ATb (7) 证：
必要性.对F ( x) || Ax b ||2 ( Ax b, Ax b) X T AT AX 2bT AX bT b 求导为：F ( x) 2 AT AX 2 AT b 若x * 是F ( x)的极小点。则必有F ( x*) 0 由此得AT AX * AT b
(i ) F t1( i ) , t 2 , tl( i ) , x1 , x2 , xn y ( i )


就是第i个实验点到该曲面的一种“距离”。 为计算方便，通常把 m
i 1
(i ) s( x1 , x2 xn ) [ F (t1 , tl( i ) , x1 xn ) y (i ) ]2
(2)
作为m个实验点到该曲面“总距离”的度量。
如何选择参数 x1…xn 使（2）达到极小这就是最 小二乘法问题。上述问题用向量形式记为：
min F ( x) - Y
其中 F ( x) = [ F (t
(1)
2
, x), F (t ( 2) , x), F (t ( m) , x)]T
t
(i )
xR

因为 AZ
2
≥0.则 AV - b
2
≥ AX - b
*
可见X *是（6）的极小点。
称形如（7）的方程组为最小二乘问题（6）的法方程组.
可见求解线性最小二乘问题等价于求解它的法方程组.
又因为
i 1
m
则有G ( x) 2 AT ( x) A( x) 2 S ( x) 先考虑无约束最优化的Newton法： 2 f ( xk )( x xk ) f ( xk )
T T 则在此处有 2 A ( x ) A ( x ) 2 S ( x ) P 2 f ( x ) f ( xk ) k k k k k
对于实际一组参数x1,x2…xn的值，（1）给出l+1 维空间中的一个超曲面。第i个实验点 （ t1(i) ,t2(i) ,…tl(i) )在（1）中就确定超曲面上一个点即 相应的函数值：
(i ) (i ) ~ y (i ) F (t1 , t2 ,tl(i ) , x1 xn )
(i ) ~ y 这个函数值 与测量值y(i)之差的绝对值
则F ( x) f ( x)T f ( x)的梯度向量g ( x) 2f ( x)T f ( x) 而F ( x)的Hessian矩阵为：G ( x) 2f ( x)T f ( x) 2 f i ( x) 2 f i ( x)
i 1 m
若令S ( x) f i ( x) 2 f i ( x)