第五章--最小二乘问题的解法

最小二乘法设（x 1, y 1 ), (x 2, y 2), …, (x n, y n)是直角平面坐标系下给出的一组数据，若x 1<x 2<…<x n,我们也可以把这组数据看作是一个离散的函数。

根据观察，如果这组数据图象“很象”一条直线（不是直线），我们的问题是确定一条直线y = bx +a ,使得它能"最好"的反映出这组数据的变化。

最小二乘法是处理各种观测数据进行测量平差的一种基本方法。

如果以不同精度多次观测一个或多个未知量，为了求定各未知量的最可靠值，各观测量必须加改正数，使其各改正数的平方乘以观测值的权数的总和为最小。

因此称最小二乘法。

所谓“权”就是表示观测结果质量相对可靠程度的一种权衡值。

法国数学家勒让德于1806年首次发表最小二乘理论。

事实上，德国的高斯于1794年已经应用这一理论推算了谷神星的轨道，但迟至1809年才正式发表。

此后他又提出平差三角网的理论，拟定了解法方程式的方法等。

为利用最小二乘法测量平差奠定了基础。

最小二乘法也是数理统计中一种常用的方法，在工业技术和其他科学研究中有广泛应用。

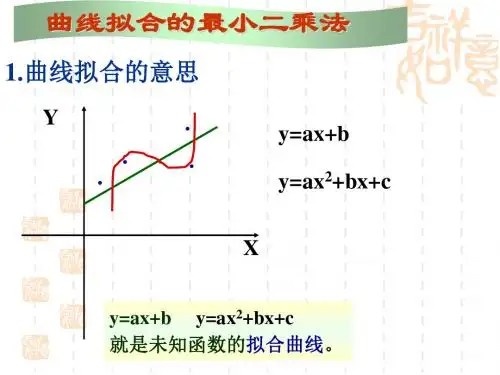
在我们研究两个变量(x, y)之间的相互关系时，通常可以得到一系列成对的数据(x1, y1、x2, y2... xm , ym)；将这些数据描绘在x -y直角坐标系中(如图1), 若发现这些点在一条直线附近，可以令这条直线方程如(式1-1)。

Y计= a0 + a1 X (式1-1)其中：a0、a1 是任意实数为建立这直线方程就要确定a0和a1，应用《最小二乘法原理》，将实测值Yi与利用(式1-1)计算值(Y计= a0+a1X)的离差(Yi-Y计)的平方和｀〔∑(Yi - Y计)2〕最小为“优化判据”。

令: φ = ∑(Yi - Y计)2 (式1-2)把(式1-1)代入(式1-2)中得:φ = ∑(Yi - a0 - a1 Xi)2 (式1-3)当∑(Yi-Y计)平方最小时，可用函数φ 对a0、a1求偏导数，令这两个偏导数等于零。

第五章 广义逆及最小二乘解在应用上见得最频繁的、大约莫过于线性方程组了。

作一番调查或整理一批实验数据，常常归结为一个线性方程组：Ax b =然而是否是相容方程呢？倘若不是，又如何处理呢？最小二乘解是常见的一种处理方法。

其实它不过是最小二乘法的代数形式而已。

广义逆从1935年Moore 提出以后，未得响应。

据说： (S.L.Campbell ＆ C.D.Meyer.Jr Generalized Inverses of Linear Transformations 1979 P9)原因之一，可能是他给出的定义，有点晦涩。

其后，1955年Penrose 给出了现在大都采用的定义以后，对广义逆的研究起了影响，三十年来，广义逆无论在理论还是应用上都有了巨大发展，一直成为了线性代数中不可缺少的内容之一。

为了讨论的顺利进行，我们在第一节中先给出点准备，作出矩阵的奇值分解。

§5.1 矩阵的酉交分解、满秩分解和奇值分解在线行空间中，知道一个线性变换在不同基偶下的矩阵表示是相抵的或等价的。

用矩阵的语言来说，就是：若 ,m n A B C ×∈，倘有非异矩阵()P m n ×，()Q n n ×存在，使B PAQ =则称A 与B 相抵的或等价的。

利用初等变换容易证明m n A C ×∈，秩为r ，则必有P ，Q ，使000r m nI PAQ C ×⎛⎞=∈⎜⎟⎝⎠(5.1-1) 其中r I 是r 阶单位阵。

在酉空间中，上面的说法，当然也成立，如果加上P ，Q 是酉交阵的要求，情形又如何呢？下面就来讨论这个问题。

定理 5.1.1 (酉交分解) m n A C ×∈，且秩为r ，则(),(),,H H m n U m n V n n U U I V V I ∃××==，使00r HU AV Δ⎛⎞=×⎜⎟⎝⎠(m n) (5.1-2) 其中r Δ为r 阶非异下三角阵。

最小二乘拟合算法最小二乘定义一般情况下，最小二乘问题求的是使某一函数局部最小的向量 x，函数具有平方和的形式，求解可能需要满足一定的约束：信赖域反射最小二乘要理解信赖域优化方法，请考虑无约束最小化问题，最小化 f(x)，该函数接受向量参数并返回标量。

假设您现在位于 n 维空间中的点 x 处，并且您要寻求改进，即移至函数值较低的点。

基本思路是用较简单的函数 q 来逼近 f，该函数需能充分反映函数 f 在点 x 的邻域 N 中的行为。

此邻域是信赖域。

试探步 s 是通过在 N 上进行最小化（或近似最小化）来计算的。

以下是信赖域子问题如果f(x + s) < f(x)，当前点更新为 x + s；否则，当前点保持不变，信赖域 N 缩小，算法再次计算试探步。

在定义特定信赖域方法以最小化 f(x) 的过程中，关键问题是如何选择和计算逼近 q（在当前点 x 上定义）、如何选择和修改信赖域 N，以及如何准确求解信赖域子问题。

在标准信赖域方法中，二次逼近 q 由 F 在 x 处的泰勒逼近的前两项定义；邻域 N 通常是球形或椭圆形。

以数学语言表述，信赖域子问题通常写作公式2其中，g 是 f 在当前点 x 处的梯度，H 是 Hessian 矩阵（二阶导数的对称矩阵），D 是对角缩放矩阵，Δ是正标量，∥ . ∥是 2-范数。

此类算法通常涉及计算 H 的所有特征值，并将牛顿法应用于以下久期方程它们要耗费与 H 的几个分解成比例的时间，因此，对于信赖域问题，需要采取另一种方法。

Optimization Toolbox 求解器采用的逼近方法是将信赖域子问题限制在二维子空间 S 内。

一旦计算出子空间 S，即使需要完整的特征值/特征向量信息，求解的工作量也不大（因为在子空间中，问题只是二维的）。

现在的主要工作已转移到子空间的确定上。

二维子空间 S 是借助下述预条件共轭梯度法确定的。

求解器将 S 定义为由 s1 和 s2 确定的线性空间，其中 s1 是梯度 g 的方向，s2 是近似牛顿方向，即下式的解或是负曲率的方向，以此种方式选择 S 背后的理念是强制全局收敛（通过最陡下降方向或负曲率方向）并实现快速局部收敛（通过牛顿步，如果它存在）。

最小二乘问题常用的那些优化方法题外话：从开始学习Slam十四讲第六章的时候就开始想写一个文档整理一下这些年遇到的优化算法，一周学一章，现在都学到第9章了，总算半整理半引用整理出来了...如果学一个东西是不断坑自己+自己去填坑的过程，下一次应该不会摔的那么疼了吧对于一个最小二乘问题的求解，根据目标函数可分为线性最小二乘和非线性最小二乘；对于非线性最小二乘问题，通常是进行泰勒展开将问题线性化，求解线性增量方程或是直接迭代找到最优值；对于线性最小二乘问题，通常是直接进行展开、求导等于零，构造\(A\vec{x}=\vec{b}\)的解方程问题，使用直接分解法或是迭代法求解；写完后发现文档较长，还是列一下有些什么东西吧：•梯度下降与其扩展算法（随机梯度下降、mini-batch梯度下降以及批梯度下降）•牛顿法与其优化算法（拟牛顿法、BFGS、LBFGS、高斯牛顿法以及列文伯格-马夸尔特法)•求解线性最小二乘问题的那些：1）直接分解（LU、LUP、Cholesky分解求解方阵线性方程组问题，QR分解解决欠定方程组问题以及超定方程组的最小二乘解）；2）迭代法（雅各比迭代、高斯赛德尔迭代、SOR以及超级好用的共轭梯度）•一些自己觉得不错的博客介绍；非线性最小二乘问题对于非线性最小二乘问题，通常会将目标函数进行泰勒展开，并将问题转换为一个线性求解问题：设有一个最小二乘问题：\[\min_{\vec{x}}F(\vec{x})=\frac{1}{2}||f(\vec{x})||_2 ^2\tag{1} \]有\(\vec{x}\in {R^n}, f\)是非线性函数，求解这个问题的常规思路是：1.给定某个初始值\(\vec{x}_0\)2.对于第k次迭代，寻找一个增量\(\Delta\vec{x}_k\)，使得\(||f(\vec{x}_k+\Delta\vec{x}_k)||_2^2\)3.\(\Delta\vec{x}_k\)足够小，则停止4.否则，令\(\vec{x}_{k+1}=\vec{x}_k +\Delta\vec{x}_k\)，返回第2步将非线性最小二乘问题求解的目标：从寻找最优值转换为寻找最小的\(\Delta\vec{x}_k\)，当函数下降到\(\Delta\vec{x}_k\)很小的时候，则等价为已找到最优值。

最小二乘估计原理一、最小二乘估计的基本原理1.建模假设：假设观测值中的噪声服从零均值的高斯分布。

2.线性假设：假设模型是线性的，即观测值与参数之间的关系可以用线性方程来表示。

3.误差假设：假设观测值中的噪声是相互独立的。

在最小二乘估计中，我们假设观测值y可以由一个线性方程表达，即：y=Xβ+ε其中，y是一个n维列向量，表示观测值；X是一个n×m维矩阵，表示观测值与参数之间的线性关系；β是一个m维列向量，表示参数；ε是一个n维列向量，表示噪声。

我们的目标是通过最小化观测值与估计值之间的误差平方和来求解参数的最优解。

即，我们要找到估计参数β使得下式最小：∑(y-Xβ)²二、最小二乘估计的问题建模在实际应用中，我们往往通过收集大量的观测数据来进行参数估计。

假设我们收集了n组观测数据，可以用一个矩阵形式来表示，即：Y=Xβ+ε其中，Y是一个n×1维矩阵，表示观测值；X是一个n×m维矩阵，表示观测值与参数之间的线性关系；β是一个m×1维矩阵，表示参数；ε是一个n×1维矩阵，表示噪声。

根据最小二乘估计的原理，我们需要求解出参数估计值β。

为了简化问题，我们可以通过最小化误差平方和来得到β的解析解。

误差平方和可以表示为：∑(Y-Xβ)²对该函数进行求导，令其导数为零，我们可以得到参数估计值的解析表达式：β=(X^TX)^(-1)X^TY三、最小二乘估计的求解方法在实际应用中，我们可以使用多种方法来求解最小二乘估计的参数。

1.解析解法：通过求解误差平方和的导数为零的方程，可以得到参数的解析解表达式。

2.矩阵分解法：通过将矩阵X进行分解，如QR分解、奇异值分解等，可以简化计算过程。

3.数值优化法：通过使用优化算法，如梯度下降法、牛顿法等，可以求解参数的数值近似解。

四、最小二乘估计的应用1.回归分析：最小二乘估计可用于拟合数据点并得到回归模型的参数，如线性回归、多项式回归等。

最小范数解和最小二乘解在数学和工程学中，最小范数解和最小二乘解是两个常用的概念。

它们在解决线性方程组和最优化问题时具有重要的意义。

最小范数解是指在所有解中，范数最小的解。

范数是一种度量向量或者矩阵大小的函数。

在线性代数中，常用的范数有L1范数、L2范数和无穷范数等。

对于给定的线性方程组Ax=b，如果存在一个向量x使得Ax=b成立，同时x的范数最小，那么x就是该线性方程组的最小范数解。

最小二乘解是指在所有解中，使得误差平方和最小的解。

在实际问题中，往往会遇到超定线性方程组，即方程组的未知数个数多于方程个数。

这时候，很可能无法找到一个精确的解使得方程组成立。

最小二乘解可以通过最小化误差平方和来找到一个最接近的解。

对于给定的超定线性方程组Ax=b，最小二乘解x可以通过求解最小化目标函数||Ax-b||2的优化问题得到。

最小范数解和最小二乘解在一些问题中具有相似的性质，但在某些情况下它们的解可能不同。

在实际应用中，最小范数解和最小二乘解都有广泛的应用。

例如，在信号处理中，最小范数解可以用于信号恢复和降噪；在图像处理中，最小范数解可以用于图像复原和去噪；在机器学习中，最小二乘解常用于线性回归和参数估计等问题。

最小范数解和最小二乘解的求解方法也有很多。

对于最小范数解，可以使用线性代数中的求解方法，如矩阵的奇异值分解（SVD）等。

对于最小二乘解，可以使用数值优化算法，如梯度下降法、牛顿法等。

这些方法可以有效地求解最小范数解和最小二乘解，并且在实际应用中具有较好的性能。

总结来说，最小范数解和最小二乘解是解决线性方程组和最优化问题中常用的概念。

它们在实际应用中具有广泛的应用价值，并且可以通过不同的数学方法和算法进行求解。

无论是在工程领域还是在科学研究中，了解和掌握最小范数解和最小二乘解的概念和求解方法都是非常重要的。

数值分析作业最小二乘法最小二乘法是提供“观测组合”的主要工具之一,它依据对某事件的大量观测而获得最佳”结果或最可能”表现形式。

如已知两变量为线性关系y= a+ bx,对其进行n(n> 2)次观测而获得n对数据。

若将这n对数据代入方程求解a，b之值则无确定解。

最小二乘法提供了一个求解方法，其基本思想就是寻找最接近”这n 个观测点的直线。

最小二乘法不仅是19世纪最重要的统计方法,而且还可以称为数理统计学之灵魂。

相关回归分析、方差分析和线性模型理论等数理统计学的几大分支都以最小二乘法为理论基础。

作为其进一步发展或纠正其不足而采取的对策,不少近现代的数理统计学分支也是在最小二乘法基础上衍生出来的。

正如美国统计学家斯蒂格勒(S.M. Stigler)所说,最小二乘法之于数理统计学犹如微积分之于数学”最小二乘法创立的历史过程充满着丰富的科学思想,这些对今日的数学创造仍有着重要的启示意义。

本文旨在全面认识最小二乘法的历史系统发育过程以及创立者的思路。

一先驱者的相关研究天文学和测地学的发展促进了数理统计学及其他相关科学的发展。

丹麦统计史家哈尔德曾指出天文学在数理统计学发展中所起的作用。

“天文学自古代至18 世纪是应用数学中最发达的领域。

观测和数学天文学给出了建立数学模型及数据拟合的最初例子,在此种意义下,天文学家就是最初的数理统计学家。

天文学的问题逐渐引导到算术平均,以及参数模型中的种种估计方法,以最小二乘法为顶峰。

” 这也说明了最小二乘法的显著地位。

有关统计计算思想记载的著作要首推天文学家罗杰柯茨的遗作,即1715年其所发论文中所蕴含的统计方法,亦即对各种观测值赋予加权后求其加权平均。

尽管当时得到认可,然而事实证明如此计算的结果不太精确。

1749年,欧拉(L. Euler,1707—1783)在研究木星和土星之间相互吸引力作用对各自轨道影响时,最后得到一个含8个未知量75个方程的线性方程组。

欧拉的求解方法繁杂而奇特,只能看作是一次尝试。

最小二乘法1：最小二乘法的原理与要解决的问题最小二乘法是由勒让德在19世纪发现的，形式如下式：标函数 = \sum（观测值-理论值）^2\\观测值就是我们的多组样本，理论值就是我们的假设拟合函数。

目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的拟合函数的模型。

举一个最简单的线性回归的简单例子，比如我们有 m 个只有一个特征的样本： (x_i, y_i)(i=1, 2, 3...,m)样本采用一般的 h_{\theta}(x) 为 n 次的多项式拟合，h_{\theta}(x)=\theta_0+\theta_1x+\theta_2x^2+...\theta _nx^n,\theta(\theta_0,\theta_1,\theta_2,...,\theta_n) 为参数最小二乘法就是要找到一组\theta(\theta_0,\theta_1,\theta_2,...,\theta_n) 使得\sum_{i=1}^n(h_{\theta}(x_i)-y_i)^2 (残差平方和) 最小，即，求 min\sum_{i=1}^n(h_{\theta}(x_i)-y_i)^22 ：最小二乘法的矩阵法解法最小二乘法的代数法解法就是对 \theta_i 求偏导数，令偏导数为0，再解方程组，得到 \theta_i 。

矩阵法比代数法要简洁，下面主要讲解下矩阵法解法，这里用多元线性回归例子来描：假设函数h_{\theta}(x_1,x_2,...x_n)=\theta_0+\theta_1x_1+...+\t heta_nx_n 的矩阵表达方式为：h_{\theta}(\mathbf{x})=\mathbf{X}\theta\\其中，假设函数 h_{\theta}(\mathbf{x})=\mathbf{X}\theta 为 m\times1 的向量, \theta 为 n\times1 的向量，里面有 n 个代数法的模型参数。

广义最小二乘法第五章广义最小二乘法当计量经济学模型同时存在序列相关和异方差,而且随机误差项的方差-协方差矩阵未知时我们可以考虑使用广义最小二乘法(gls)。

即下列模型：y=xβ+μ满足这样一些条件：e(μ)=0cov(μμ')=δ2ωω=11ω1221ω221ωn2...ω1n...ω2nωnn设立ω=dd'用d左乘y=xβ+μ的两边，得到一个新的模型d-1y=d-1xβ+d-1μy=x**-1β+μ*（1）该模型具备同方差性和随机误差相互独立性。

因为可以证明：e(μ*μ*')=δ2i于是需用普通最轻二乘法估算（1）式，获得的参数估计结果为ˆ=(x*'x*)-1x*'y*β=(x'ωx)x'ωy整个过程最重要的一步就是要估计ω，当模型存在一阶自相关时。

我们取-1-1-1ρn-1ρn-2ρn-1ρn-21案例四：广义最小二乘法在这里我们举例子去表明广义最轻二乘法的应用领域。

在探讨这个问题时所使用的数据如下表中5.1右图：首先我们计算ρ，我们可以直接根据ols估计出来的dw来计算，ols估计出来的结果为下表5.2：可以根据ρ=1-dw/2，dw=0.8774，因此ρ=0.5613,在这个基础上,我们可以得出结论这个方差-协方差矩阵。

方差协方差矩阵可以由以下一个程序去赢得：!p=0.5613matrix(17,17)fac1for!i=1to17fac1(!i,!i)=1for!j=1to17for!i=!j+1to17fac1(!i,!j)=!p^(!i-!j)fac1(!j,!i)=fac1(!i,!j)得到的矩阵结果为下表5.3下面再展开cholosky水解,获得d,展开cholosky水解时所用至的命令如下:1sym(17,17)fact1matrixfact1=@cholesky(fact)得到的fact1矩阵如下解fact1的逆矩阵就可以将数据展开切换,获得m2和gdp,解逆矩阵时使用的命令如下:matrix(17,17)fact2**fact2=@inverse(fact)得到的fact1矩阵的逆矩阵fact2如下m2*=m2*fact2gdp*=gdp*fact这样就可以获得一组转换后的数据,数据如下再对这组数据进行普通最小二乘法就可以得到这个方程的广义最小二乘法的估计结果,结果如下:可以看见，采用广义最轻二乘法后，序列有关的情况获得提升。

第五章 最小二乘问题的解法1.最小二乘问题 1)回归方程问题[]Ti i l i y t t)()()(1,,...,,m i ,...,2,1=是m 个实验点。

现要根据这些点确定y 与l 个物理量l t t t ,...,,21之间的关系式。

设这种关系式为),...,,,...,(11n l x x t t F y =，其中n x x ,...,1是方程中需要待定的n 个参数(系数)。

因此问题是如何通过)(n m m >个实验点，确定方程中的系数。

由于实验点的个数大于待定系数的个数，因此方程中系数的确定是一个超静定问题，无法按一般的方法进行求解。

此时将实验点到曲面距离最短的那个曲面作为所求曲面，从而求取该曲面方程。

即求解[]∑=-mi i i y x t F 12)()(),(min ，这就是最小二乘问题。

2)非线性方程组问题求解非线性方程组⎪⎪⎩⎪⎪⎨⎧===0),...,(............................0),...,(0),...,(11211n n nn x x f x x f x x f 可转化为求解如下形式的最小二乘问题。

∑=mi n i x x f112),...,(min显而易见，最小二乘法的一般形式可写为)()(min x f x f T最小二乘法问题实际上是具有n 个变量的无约束极小化问题，前面解无约束优化问题的方法均可应用。

但是最小二乘问题具有一定的特殊性，即目标函数的表达式是由多个表达式的平方和组成，理应有更、更有效的方法。

这正是最小二乘解法要解决的问题。

2.线性最小二乘问题的解法最小二乘法的一般形式可写为)()(min x f x f T特别地，当b Ax x f -=)(，即)(x f 为线性函数时，则最小二乘问题可表示为：2min b Ax -1) 线性最小二乘问题解的条件定理1:*x 是线性最小二乘问题极小点的充要条件是*x 满足b A Ax A T T =。