下载文档原格式
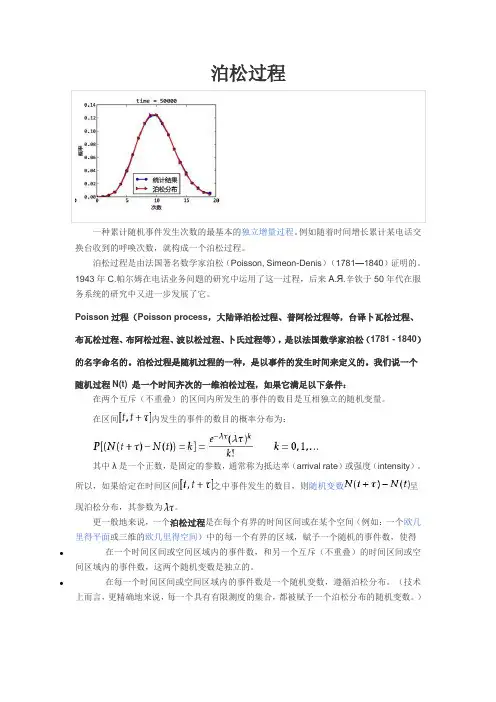
泊松过程一种累计随机事件发生次数的最基本的独立增量过程。
例如随着时间增长累计某电话交换台收到的呼唤次数，就构成一个泊松过程。
泊松过程是由法国著名数学家泊松（Poisson, Simeon-Denis）（1781—1840）证明的。
1943年C.帕尔姆在电话业务问题的研究中运用了这一过程，后来Α.Я.辛钦于50年代在服务系统的研究中又进一步发展了它。
Poisson过程（Poisson process，大陆译泊松过程、普阿松过程等，台译卜瓦松过程、布瓦松过程、布阿松过程、波以松过程、卜氏过程等），是以法国数学家泊松（1781 - 1840）的名字命名的。
泊松过程是随机过程的一种，是以事件的发生时间来定义的。
我们说一个随机过程N(t) 是一个时间齐次的一维泊松过程，如果它满足以下条件：在两个互斥（不重叠）的区间内所发生的事件的数目是互相独立的随机变量。
在区间内发生的事件的数目的概率分布为：其中λ是一个正数，是固定的参数，通常称为抵达率（arrival rate）或强度（intensity）。
所以，如果给定在时间区间之中事件发生的数目，则随机变数呈现泊松分布，其参数为。
更一般地来说，一个泊松过程是在每个有界的时间区间或在某个空间（例如：一个欧几里得平面或三维的欧几里得空间）中的每一个有界的区域，赋予一个随机的事件数，使得•在一个时间区间或空间区域内的事件数，和另一个互斥（不重叠）的时间区间或空间区域内的事件数，这两个随机变数是独立的。
•在每一个时间区间或空间区域内的事件数是一个随机变数，遵循泊松分布。
（技术上而言，更精确地来说，每一个具有有限测度的集合，都被赋予一个泊松分布的随机变数。
）泊松过程是莱维过程（Lévy process）中最有名的过程之一。
时间齐次的泊松过程也是时间齐次的连续时间Markov过程的例子。
一个时间齐次、一维的泊松过程是一个纯出生过程，是一个出生-死亡过程的最简单例子。
第7章 马尔可夫过程与泊松过程7.1 马尔可夫过程1．引例例1：随机游动问题。
质点在一直线上作随机游动，如果某一时刻质点位于点i ，则下一步质点以概率p 向左移动一格达到点1-i ，以概率)1(p -向右移动一格达到点1+i 。
用)(n X 表示时刻n 质点的位置，则)(n X 是一随机过程。
在时刻1+n 质点所处的位置)1(+n X 只与时刻n 质点的位置)(n X 有关，而与n 以前的位置)1(-n X …)2(X 、)1(X 无关。
例2：遗传病问题。
某些疾病常遗传给下一代，但不隔代遗传。
第1+n 代是否有此种疾病只与第n 代是否有此疾病有关，而与n 代以前的健康状况无关。
2．马尔可夫过程描述性概念一般而言，若随机过程在时刻n t 所处的状态)(n t X 为已知的条件下，过程在时刻t （n t t >）所处的状态)(t X 只与过程在时刻n t 的状态)(n t X 有关，而与n t 以前的状态无关，则称此过程为马尔可夫过程。
3．马尔可夫过程分类马尔可夫过程分为四类：（1） 离散马尔可夫链：时间t 取离散值1t ， ,2t ,n t ，可直接记为 ,,2,1n t =。
状态)(n X 取离散值1a ， ,2a ,n a ，可直接记为 ,,2,1n X =。
（2） 连续马尔可夫链：时间t 取离散值1t ， ,2t ,n t ，状态)(n X 取连续值。
（3） 离散马尔可夫过程：时间t 取连续值，状态)(t X 取离散值。
（4） 连续马尔可夫过程：时间t 取连续值，状态)(t X 取连续值。
.4．马尔可夫过程的研究与应用概况在随机过程的研究领域，马尔可夫过程是主要的研究对象，有关的专著、专题无计其数，其原因是马尔可夫过程与众多的应用领域有关联。
5．马尔可夫链（1）定义设时间t 取离散值 ,,2,1n t =，记)(n X X n =，设状态n X 取有限个离散值N X ,2,1=，若{}{}i X j X P i X i X i X j X P n n n n n n =======+--+111111,,称n X 马尔可夫链。
21021210分布马尔可夫过程及其概率1§马尔可夫过程的定义、1211111121.简称马氏链可夫链，马尔可夫过程称为马尔时间和状态都是离散的课稿南京邮电大学孔告化讲22110}|{),(i m j n m i j a X a X P n m m P ===++记马氏链的转移概率、221021210.),(的转移概率转移到状态在时刻条件下，处于状态为马氏链在时刻称j i i j a n m a m n m m P ++课稿南京邮电大学孔告化讲.))(()(步转移概率矩阵为称n n P n P i j =⎟⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎜⎝⎛==M ML M M L L L M L M M L L L L )()()()()()()()()())(()(212222111211n P n P n P n P n P n P n P n P n P n P n P N N N N N N i j LLN a a a 21MM N a a a 21矩阵齐次马氏链的转移概率、3Ia a n P j i i j ∈≥,0)()1(Ia n P i j i j ∈=∑∞=1)()2(1课稿南京邮电大学孔告化讲111⎟⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎜⎝⎛==M M L M M L L L M L M M L L L L N N N N N N p p p p p p p p p P P 212222111211)1(L L N a a a 21M M N a a a 211课稿南京邮电大学孔告化讲这一点上。
或移动到就以概率，则下一时刻或现在位于点的概率停在原处；如果一格，或以的概率向左或向右移动则下一时刻各以现在位于点是：如果发生游动。
游动的规则等时刻秒秒、仅在上作随机游动，并且仅在如图所示直线的点集设一醉汉一维随机游动例题)4(21)5(13/13/1),51(21}5,4,3,2,1{)(:Q i i Q I Q <<=L 12345过程，是一随机则的位置，时表示时刻若以},2,1,0,{L =n X Q n X n n 而且当时，等以后的行为只与有关，而与质点以前是如何到是完全无关的，所以，它是一个马氏链，且为齐次马氏链。
