例5-12(债券久期计算)

债券久期的计算公式债券久期是指在给定利率环境下，债券现金流的加权平均到期时间。

它是债券价格对利率的敏感性的度量，通常用于估计债券价格的变动。

下面将介绍债券久期的计算公式及其相关概念。

首先需要了解以下几个概念：1.票息支付：债券持有人每年（或每半年）获得的利息支付。

2.本金偿还：债券到期时归还给持有人的本金。

3.利率变化：市场上的利率在其中一时间段内发生的变化。

1.票息久期的计算公式：票息久期表示债券上的现金流与票息支付之间的关联程度。

它衡量的是当利率发生变化时，票息支付变动对债券价格变动的敏感性。

票息久期的计算公式为：票息久期=(每期现金流的现值乘以到期时间的加权平均值)/债券的当前价格计算公式中的每期现金流的现值表示债券每一期的利息支付，到期时间表示从当前时间到每一期现金流到期的剩余时间。

2.本金久期的计算公式：本金久期表示债券价格与本金偿还之间的关联程度。

它衡量的是当利率发生变化时，本金偿还对债券价格变动的敏感性。

本金久期的计算公式为：本金久期=(每期现金流的现值乘以到期时间的加权平均值)/债券的当前价格计算公式中的每期现金流的现值表示债券每一期给予持有人的本金偿还，到期时间表示从当前时间到每一期现金流到期的剩余时间。

3.债券久期的计算公式：债券久期是票息久期和本金久期之和。

债券久期=票息久期+本金久期债券久期=[(每期现金流的现值乘以到期时间的加权平均值)/债券的当前价格]+[(每期现金流的现值乘以到期时间的加权平均值)/债券的当前价格]票息久期和本金久期的计算公式非常相似，只是现金流的现值乘以到期时间的加权平均值的计算方式有所不同。

在实际计算中，可以使用电子表格软件（如Excel）中的内置函数来计算债券久期。

这些函数包括NPV（现值）、WEIGHTED AVERAGE（加权平均）等。

需要注意的是，久期只是一种理论上的估算值，并不代表实际到期时间。

实际情况中，债券的回收率、违约风险等因素可能会对久期产生影响。

债券久期计算范文债券久期是债券的一个重要指标，用于衡量债券价格对利率变动的敏感度。

在债券投资中，了解债券久期的计算方法和影响因素对于投资者做出明智的投资决策至关重要。

首先，我们需要了解什么是债券久期。

债券久期是一个衡量债券价格对利率变动的敏感度指标。

它告诉投资者，在债券持有到期之前，每一次1%的利率变动对债券的价格有多大的影响。

债券久期越长，利率变动对债券价格的影响越大，债券的价格波动性越高。

债券久期的计算方法有多种方式，其中最常见的是修正久期。

修正久期考虑了债券的剩余期限、每期现金流量和债券价格。

以一个简单的固定利率债券为例，债券期限为N年，票息率为C，面值为F，债券的价格为P。

首先，我们需要计算债券的现金流量，即每年的票息支付和到期时的回本支付。

然后，乘以各期现金流量的加权比例，得到修正久期。

修正久期的计算公式如下：修正久期=∑[t*CFt/(1+r)^t]/P其中，t代表现金流发生的时间点，CFt表示现金流，r表示久期的折现率，P表示债券的价格。

在计算修正久期时，需要注意的是，债券价格和利率有着相反的变动关系，即债券价格上升，利率下降；债券价格下降，利率上升。

因此，在计算修正久期时，利率应该取负值。

为了更好地理解债券久期的概念和计算方法，我们来看一个具体的例子。

假设一只债券面值为1000元，期限为5年，票息率为5%，即每年支付50元的票息。

当前市场利率为6%。

根据这些信息，我们可以计算出该债券的修正久期。

首先，我们需要计算每一年的现金流。

在第1年、第2年、第3年、第4年，债券发行人分别支付50元的票息，第5年支付50元的票息和面值1000元的本金回收。

其次，我们需要计算每一年现金流的加权比例。

由于每一年现金流的发生时间点相等，所以加权比例为1/5=0.2然后，我们需要将现金流按照久期的折现率折现，即除以(1+r)^t。

在这个例子中，折现率r等于市场利率-利息率，即6%-5%=1%。

现金流折现后，我们可以得到如下结果：第1年现金流：50/(1+1%)^1=49.5第2年现金流：50/(1+1%)^2=48.5第3年现金流：50/(1+1%)^3=47.5第4年现金流：50/(1+1%)^4=46.6第5年现金流：(50+1000)/(1+1%)^5=1053.1最后，我们将每一年的现金流乘以加权比例，并将结果相加，即可得到修正久期的计算结果：修正久期=[1*(49.5)+2*(48.5)+3*(47.5)+4*(46.6)+5*(1053.1)]/(1000)=4.23年根据修正久期的计算结果，我们可以得出以下几点分析：1.该债券的修正久期为4.23年，表示在当前市场利率下，每次1%的利率变动将导致债券价格的大约4.23%的变动。

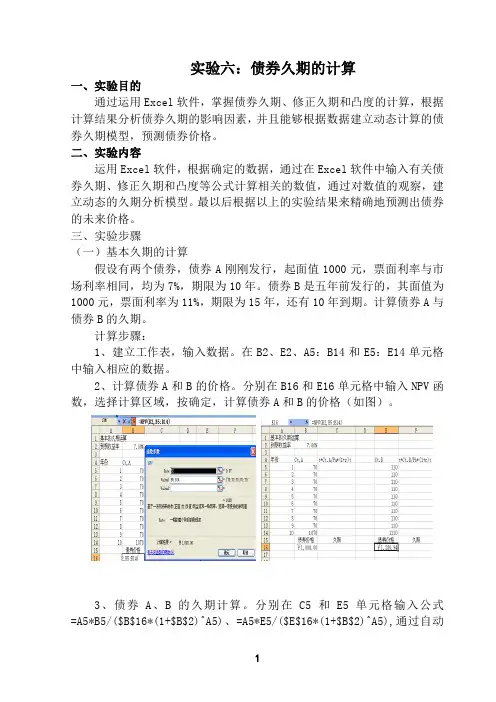
实验六：债券久期的计算一、实验目的通过运用Excel软件，掌握债券久期、修正久期和凸度的计算，根据计算结果分析债券久期的影响因素，并且能够根据数据建立动态计算的债券久期模型，预测债券价格。

二、实验内容运用Excel软件，根据确定的数据，通过在Excel软件中输入有关债券久期、修正久期和凸度等公式计算相关的数值，通过对数值的观察，建立动态的久期分析模型。

最以后根据以上的实验结果来精确地预测出债券的未来价格。

三、实验步骤（一）基本久期的计算假设有两个债券，债券A刚刚发行，起面值1000元，票面利率与市场利率相同，均为7%，期限为10年。

债券B是五年前发行的，其面值为1000元，票面利率为11%，期限为15年，还有10年到期。

计算债券A与债券B的久期。

计算步骤：1、建立工作表，输入数据。

在B2、E2、A5：B14和E5：E14单元格中输入相应的数据。

2、计算债券A和B的价格。

分别在B16和E16单元格中输入NPV函数，选择计算区域，按确定，计算债券A和B的价格（如图）。

3、债券A、B的久期计算。

分别在C5和E5单元格输入公式=A5*B5/($B$16*(1+$B$2)^A5)、=A5*E5/($E$16*(1+$B$2)^A5),通过自动填充单元格命令格式求出C5和F5单元区域的数据（如图）。

分别在C16和F16单元格输公式=SUM（C5：C14）和=SUM（F5：F14），按回车键，分别算出债券A和B的久期（如图）。

从计算结果来看，虽然债券A与债券B的到期期限都是10年，但债券A的久期大于债券B的久期。

（二）久期作为债券价格相对利率的弹性的计算。

已知债券A刚刚发行，其面值为1000元，票面利率为7%，期限为10年；债券B是5年前发行的，其面值为1000元，票面利率为11%，期限为15年，还有10年到期。

假设市场利率（贴现率）从当前的7%增加到7.02%。

请计算：（1）计算债券A与债券B的市场价格变化率；（2）作为债券价格相对市场利率的弹性来估计债券A、B的久期。

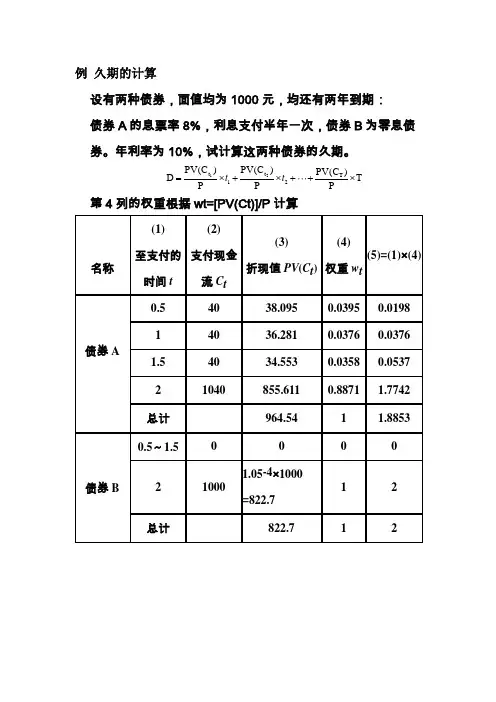
例 久期的计算
设有两种债券，面值均为1000元，均还有两年到期： 债券A 的息票率8%，利息支付半年一次，债券B 为零息债券。

年利率为10%，试计算这两种债券的久期。

第4列的权重根据wt=[PV(Ct)]/P 计算
PV (C t ) (4)
权重38.095 0.039536.281 0.037634.553
0.0358855.611 0.8871964.54 1000
T PV(C P
+
+
连续复利是指在期数趋于无限大的极限情况下得到的利率，此时不同期之间的间隔很短，可以看作是无穷小量。

设本金为p 0 ，年利率为r ，当每年含有m 个复利结算周期（若一个月为一个复利结算周期，则m=12，若以一季度为一个复利结算周期，则m=4）时，则n 年后的本利和为：
所以当连续复利本利和公式为：
即：
在连续复利下，久期的表达式可以写成：
1
1
1
1
D i
i
i rt n
n
rt i i i i n rt i i i
t c t e
c t e p c e ---=====∑
∑∑1mn
nr r/m
mn 00r r p =p 1p 1m m ⎛
⎫⎛
⎫+=+ ⎪
⎪
⎝⎭
⎝⎭
1/000r r lim 1lim 1m m nr
mn
r m
nr n m m p p p p e →∞→∞⎡
⎤
⎛
⎫⎛⎫⎢⎥=+=+= ⎪
⎪
⎢⎥⎝⎭
⎝⎭
⎣
⎦
00nr n nr
n p p e p p e -==。

债券久期计算-计算债券久期例题例：假设债券A刚发行，其面值为1000元，市场利率（贴现率8%），票面利率为8%，期限为十年。

债券B是5年前发行的，其面值为1000元，票面利率12%，期限为15年，还有10年到期。

计算：1债券A与债券B的价格2计算债券A和B的久期三种方法1）运用久期的定义：久期作为现金流支付时间的加权平均（2）将久期看作债券价格对贴现率的弹性3）运用久期函数3计算债券A，B的修正久期4如果市场利率上升10%，即从8%上升到8.8%，求债券A与债券B的价格的变化久期（n）一、久期(n)的概念久期的概念最早是XXX(Macaulay)在1938年提出来的，所以又称马考勒久期（简记为D）。

马考勒久期是使用加权平均数的形式计算债券的平均到期时间。

它是债券在未来产生现金流的时间的加权平均,其权重是各期现金值在债券价格中所占的比重。

具体的计算将每次债券现金流的现值除以债券价格得到每一期现金支付的权重，并将每一次现金流的时间同对应的权重相乘,最终合计出整个债券的久期。

XXX、XXX和XXX在随后的若干年独立地发现了久期这一理论范畴，特别是XXX和XXX将久期用于衡量资产/负债的利率敏感性的研究，使得久期具有了第二种含义，即：资产针对利率变化的价格变化率。

久期--的第二个含义是债券投资管理中的一个极其重要的战略----“免疫战略”的理论基础，根据该战略，当交易主体债券组合的久期与债务的持有期相等的时候，该交易主体短期内就实现了“免疫”的目标，即短期内的总财产不受利率波动的影响。

但是应用这一战略的前提则是，现有久期观点能否正确地衡量未来任何利率变动情形下债券代价的变动情况。

二、马考勒久期的计算公式公式1)其中，D是马考勒久期，B是债券当前的市场价格，PV （Ct）是债券未来第t期可现金流（利息或资本）的现值，T是债券的到期时间。

需要指出的是在债券发行时以及发行后，都可以计算马考勒久期。

计算发行时的马考勒久期，T（到期时间）等于债券的期限；计算发行后的马考勒久期，T（到期时间）小于债券的期限。

久期(Duration)的概念久期的概念最早是马考勒(Macaulay)在1938年提出来的，所以又称马考勒久期（简记为D）。

马考勒久期是使用加权平均数的形式计算债券的平均到期时间。

它是债券在未来产生现金流的时间的加权平均,其权重是各期现金值在债券价格中所占的比重。

具体的计算将每次债券现金流的现值除以债券价格得到每一期现金支付的权重，并将每一次现金流的时间同对应的权重相乘,最终合计出整个债券的久期。

马考勒久期的计算公式(公式1)其中，D是马考勒久期，B是债券当前的市场价格，PV（Ct）是债券未来第t期现金流（利息或资本）的现值，T是债券的到期时间。

需要指出的是在债券发行时以及发行后，都可以计算马考勒久期。

计算发行时的马考勒久期，T（到期时间）等于债券的期限；计算发行后的马考勒久期，T（到期时间）小于债券的期限。

任一金融工具的久期公式一般可以表示为[1]：(公式2)其中：D为久期；t为该金融工具现金流量所发生的时间；C t为第t期的现金流；F为该金融工具的面值或到期日价值；n为到期期限；i是当前的市场利率。

实际上，公式(公式3)的分母正是该金融工具的市场价值，因此，久期公式又可表示为：(公式3)其中：P表示该金融工具的市场价值或价格。

[编辑]久期的计算过程举例[1]下面试举一例来说明久期的计算过程。

假设面额为1000元的3年期变通债券，每年支付一次息票，年息票率为10%，此时市场利率为12%，则该种债券的久期为：(年)如果其他条件不变，市场利率下跌至5%，此时该种债券的久期为：(年)同理，如果其他条件不变，市场利率上升至20%，此时久期为：(年)再者，如果其他条件不变，债券息票率为0，那么：(年)从上面的计算结果可以发现，久期随着市场利率的下降而上升，随着市场利率的上升而下降，这说明两者存在反比关系。

此外，在持有期间不支付利息的金融工具，其久期等于到期期限或偿还期限。

那些分期付息的金融工具，其久期总是短于偿还期限，是由于同等数量的现金流量，早兑付的比晚兑付的现值要高。

债券久期计算在金融领域，债券是一种常见的投资工具。

对于投资者来说，了解债券的各种特性和指标至关重要，其中债券久期就是一个关键的概念。

债券久期不仅能帮助投资者评估债券价格对利率变动的敏感性，还能为投资决策提供重要参考。

那么，什么是债券久期？又该如何计算呢？首先，我们来理解一下债券久期的基本概念。

简单来说，债券久期是衡量债券价格对利率变动敏感性的一个指标。

它反映了债券现金流的平均回收时间。

为了更深入地理解债券久期，我们需要先了解债券的一些基本特征。

债券通常会在未来的特定时间点向投资者支付固定的利息，并在到期时偿还本金。

这些利息和本金的支付构成了债券的现金流。

接下来，我们探讨一下债券久期的计算方法。

目前，常用的债券久期计算方法主要有麦考利久期和修正久期。

麦考利久期的计算相对复杂一些。

它的计算公式是：麦考利久期＝（各期现金流现值×时间加权求和）÷债券价格现值。

我们通过一个简单的例子来看看麦考利久期的计算过程。

假设某债券每年支付利息 50 元，期限为 3 年，面值 1000 元，当前市场利率为8%。

首先，计算每年利息的现值。

第一年利息的现值＝ 50 ÷（1 ＋ 8%）＝ 4630 元；第二年利息的现值＝ 50 ÷（1 ＋ 8%）²＝ 4287 元；第三年利息的现值＝ 50 ÷（1 ＋ 8%）³＝ 3969 元。

然后，计算本金的现值＝ 1000 ÷（1 ＋ 8%）³＝ 79383 元。

接下来，计算各期现金流现值乘以时间的加权和：（4630×1）＋（4287×2）＋（3969×3 ＋ 79383×3）＝ 277874 元。

最后，计算债券价格现值＝ 4630 ＋ 4287 ＋ 3969 ＋ 79383 ＝92269 元。

则麦考利久期＝277874 ÷ 92269 ≈ 299 年。