南京航空航天大学《机械振动》考研复习模拟题

《机械振动噪声学》习题集1－1 阐明下列概念，必要时可用插图。

(a) 振动；机械或结构在平衡位置附近的往复运动称为机械振动。

(b) 周期振动和周期；能用时间的周期函数表示系统相应的振动叫做周期振动，周期振动完全重复一次的时间叫做周期(c) 简谐振动。

能用一项时间的正弦，余弦表示系统响应的振动叫做简谐振动振幅：物体离开平衡位置的最大位移频率：每一秒重复相同运动的次数相位角：1－2 一简谐运动，振幅为0.20 cm，周期为0.15 s，求最大的速度和加速度。

最大速度=A*w 最大加速度=A*W*W1－3 一加速度计指示结构谐振在82 Hz 时具有最大加速度50 g，求其振动的振幅。

a =A*W*W=A*(2*PI*f)*(2*PI*f)------将f=82,a=500代入即可1－4 一简谐振动频率为10 Hz，最大速度为4.57 m/s，求其振幅、周期和最大加速度。

略（方法同上一题）1－5 证明两个同频率但不同相位角的简谐运动的合成仍是同频率的简谐运动。

即：A cos ωn t +B cos (ωn t + φ) =C cos (ωn t + φ' )，并讨论φ＝0、π/2 和π三种特例。

将两个简谐运动化成复数形式即可相加1－6 一台面以一定频率作垂直正弦运动，如要求台面上的物体保持与台面接触，则台面的最大振幅可有多大？设台面运动频率为f, 即要求a=A*W*W =A*(2*PI*f)*(2*PI*f)<=g1－7 计算两简谐运动x1 = X1 cos ω t和x2 = X2 cos (ω + ε ) t之和。

其中ε << ω。

如发生拍的现象，求其振幅和拍频。

1－8 将下列复数写成指数A e i θ形式：(a) 1 + i3(b) -2 (c) 3 / (3- i ) (d) 5 i (e) 3 / (3- i ) 2(f) (3+ i ) (3 + 4 i ) (g) (3- i ) (3 - 4 i ) (h) [ ( 2 i ) 2 + 3 i + 8 ]2－1 钢结构桌子的周期τ＝0.4 s，今在桌子上放W = 30 N 的重物，如图2－1所示。

1振动测试习题8-1某车床加工外圆表面时，表面振纹主要由转动轴上齿轮的不平衡惯性力而使主轴箱振动所引起。

振纹的幅值谱如题图8.1a 所示，主轴箱传动示意图如题图8.1b 所示。

传动轴I 、传动轴II 和主轴III 上的齿轮齿数为301=z ，402=z ，203=z ，504=z 。

传动轴转速I n =2000r/min 。

试分析哪一根轴上的齿轮不平衡量对加工表面的振纹影响最大？为什么？ 8-2用压电式加速度传感器及电荷放大器测量振动，若传感器灵敏度为7pC/g ，电荷放大器灵敏度为100mV/pC ，试确定输入a =3g 时系统的输出电压。

8-3若某旋转机械的工作转速为3000转/分，为分析机组的动态特性，需要考虑的最高频率为工作频率的10倍，问：1) 应选择何种类型的振动传感器，并说明原因？2) 在进行A/D 转换时，选用的采样频率至少为多少？2习题答案8-1某车床加工外圆表面时，表面振纹主要由转动轴上齿轮的不平衡惯性力而使主轴箱振动所引起。

振纹的幅值谱如题图8.1a 所示，主轴箱传动示意图如题图8.1b 所示。

传动轴I 、传动轴II 和主轴III 上的齿轮齿数为301=z ，402=z ，203=z ，504=z 。

传动轴转速I n =2000r/min 。

试分析哪一根轴上的齿轮不平衡量对加工表面的振纹影响最大？为什么？解：传动轴轴频 336020006011===n f Hz Ⅱ轴轴频 2540/3033/2112=⨯==z z f f HzⅢ轴轴频 1050/2025/4323=⨯==z z f f Hz 因幅值最大处25Hz 对应Ⅱ轴轴频，所以Ⅱ轴上的齿轮不平衡量对加工表面的振纹影响最大8-2用压电式加速度传感器及电荷放大器测量振动，若传感器灵敏度为7pC/g ，电荷放大器灵敏度为100mV/pC ，试确定输入a =3g 时系统的输出电压。

解：输出电压 210010073=⨯⨯=u mV=2.1V8-3若某旋转机械的工作转速为3000转/分，为分析机组的动态特性，需要考虑的最高频率为工作频率的10倍，问：1) 应选择何种类型的振动传感器，并说明原因？2) 在进行A/D 转换时，选用的采样频率至少为多少？解：工作频率 5060/3000==n f Hz最高频率 500501010max =⨯==n f f Hz跟据频响范围可选电涡流式位移传感器，磁电式速度传感器，压电式加速度传感器。

机械振动考试题和答案一、单项选择题（每题2分，共20分）1. 简谐运动的振动周期与振幅无关，与（）有关。

A. 质量B. 频率C. 弹簧常数D. 初始条件答案：C2. 阻尼振动中，振幅逐渐减小的原因是（）。

A. 系统内部摩擦B. 外部阻力C. 系统内部摩擦和外部阻力D. 系统内部摩擦或外部阻力答案：C3. 两个简谐运动合成时，合成运动的频率等于（）。

A. 两个简谐运动频率之和B. 两个简谐运动频率之差C. 两个简谐运动频率中较大的一个D. 两个简谐运动频率中较小的一个答案：D4. 受迫振动的频率与（）有关。

A. 驱动力频率B. 系统固有频率C. 驱动力大小D. 系统阻尼系数答案：A5. 阻尼振动中，阻尼系数越大，振动周期（）。

A. 越大B. 越小C. 不变D. 无法确定答案：B6. 受迫振动中，当驱动力频率接近系统固有频率时，会发生（）。

A. 共振B. 反共振C. 振动增强D. 振动减弱答案：A7. 简谐运动的振动周期与（）成正比。

B. 频率C. 弹簧常数D. 质量的平方根答案：D8. 阻尼振动中，阻尼系数越小，振动周期（）。

A. 越大B. 越小C. 不变D. 无法确定答案：C9. 受迫振动中，当驱动力频率等于系统固有频率时，振动的振幅（）。

A. 最小C. 不变D. 无法确定答案：B10. 简谐运动的振动周期与（）无关。

A. 质量B. 频率C. 弹簧常数D. 初始条件答案：D二、多项选择题（每题3分，共15分）11. 简谐运动的振动周期与以下哪些因素有关？（）A. 质量C. 弹簧常数D. 初始条件答案：AC12. 阻尼振动中，振幅逐渐减小的原因包括（）。

A. 系统内部摩擦B. 外部阻力C. 系统内部摩擦和外部阻力D. 系统内部摩擦或外部阻力答案：CD13. 两个简谐运动合成时，合成运动的频率等于以下哪些选项？（）A. 两个简谐运动频率之和B. 两个简谐运动频率之差C. 两个简谐运动频率中较大的一个D. 两个简谐运动频率中较小的一个答案：BD14. 受迫振动的频率与以下哪些因素有关？（）A. 驱动力频率B. 系统固有频率C. 驱动力大小D. 系统阻尼系数答案：AB15. 阻尼振动中，阻尼系数越大，振动周期的变化情况是（）。

大学机械振动考试题目及答案一、选择题（每题2分，共10分）1. 在简谐振动中，振幅与振动的能量关系是（）。

A. 无关B. 成正比C. 成反比D. 振幅越大，能量越小答案：B2. 下列哪个不是机械振动系统的自由度？（）。

A. 转动B. 平动C. 振动D. 形变答案：C3. 一个单自由度系统在受到初始条件激励后，其振动形式是（）。

A. 简谐振动B. 阻尼振动C. 受迫振动D. 自由振动答案：D4. 在阻尼振动中，如果阻尼系数增加，振动的振幅将（）。

A. 增加B. 不变C. 减小D. 先增加后减小答案：C5. 对于一个二自由度振动系统，其振动模态数量是（）。

A. 1B. 2C. 3D. 4答案：B二、填空题（每题2分，共10分）6. 一个物体做自由振动时，其频率称为______。

答案：固有频率7. 当外力的频率与系统的固有频率相等时，系统发生的振动称为______。

答案：共振8. 阻尼力与速度成正比的阻尼称为______阻尼。

答案：线性9. 振动系统的动态响应可以通过______分析法求解。

答案：傅里叶10. 在转子动力学中，临界转速是指转子发生______振动的转速。

答案：自激三、简答题（每题5分，共20分）11. 简述什么是简谐振动，并说明其运动方程的形式。

答案：简谐振动是一种周期性的振动，其加速度与位移成正比，且方向相反。

在数学上，简谐振动的运动方程可以表示为：x(t) = A * cos(ωt + φ)其中，A 是振幅，ω 是角频率，t 是时间，φ 是初相位。

12. 解释什么是阻尼振动，并说明其特点。

答案：阻尼振动是指在振动系统中存在能量耗散，导致振幅随时间逐渐减小的振动。

其特点包括振幅逐渐衰减，振动频率可能会随着振幅的减小而发生变化，且阻尼力通常与振动速度成正比。

13. 描述什么是受迫振动，并给出其稳态响应的条件。

答案：受迫振动是指系统在周期性外力作用下的振动。

当外力的频率接近系统的固有频率时，系统将发生共振，此时振幅会显著增大。

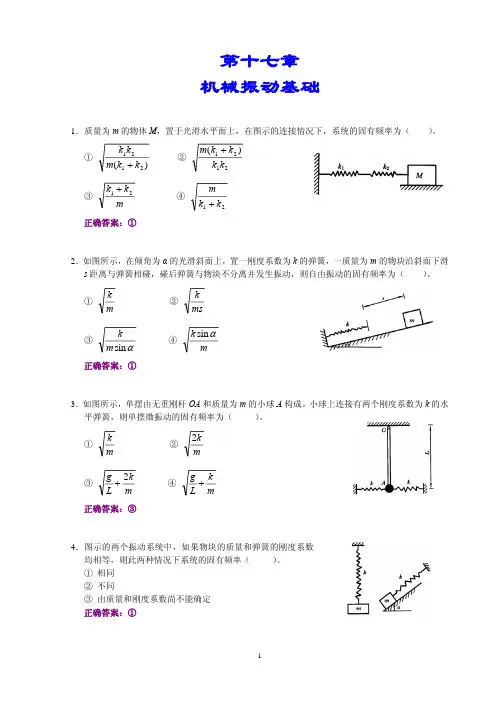
第十七章机械振动基础1．质量为m 的物体M ，置于光滑水平面上，在图示的连接情况下，系统的固有频率为（ ）。

① )(2121k k m k k + ② 2121)(k k k k m + ③m k k 21+ ④ 21k k m + 正确答案：①2．如图所示，在倾角为α的光滑斜面上，置一刚度系数为k 的弹簧，一质量为m 的物块沿斜面下滑s 距离与弹簧相碰，碰后弹簧与物块不分离并发生振动，则自由振动的固有频率为（ ）。

① mk ② ms k ③αsin m k ④ m k αsin 正确答案：①3．如图所示，单摆由无重刚杆OA 和质量为m 的小球A 构成。

小球上连接有两个刚度系数为k 的水平弹簧，则单摆微振动的固有频率为（ ）。

① mk ② m k 2 ③m k L g 2+ ④ m k L g + 正确答案：③4．图示的两个振动系统中，如果物块的质量和弹簧的刚度系数均相等，则此两种情况下系统的固有频率（ ）。

① 相同② 不同③ 由质量和刚度系数尚不能确定正确答案：①5．图示质量弹簧系统，已知物块的质量为m ，弹簧的刚度系数为k ，静伸长为δs ，原长是l 0 。

若以弹簧未伸长的下端点为坐标原点O ，则物块的运动微分方程为（ ）。

① 0=+x mk x ② 0)(=−+s x mk x δ ③ g x mk x s =−+)(δ ④ 0)(=++s x mk x δ 正确答案：②6．在图示中，当把弹簧原长的中点O 固定后，系统的固有频率与原来固有频率的比值为（ ）。

① 21 ② 2③ 2④ 4正确答案：③7．图示弹簧秤，秤盘重未知，当盘上放一重P 的物体时，测得振动周期为T 1；换一重Q 的物体时，其振动周期为T 2，则弹簧的刚度系数应为k =（ ）。

正确答案：)()(421222T T g P Q −−π8．图示为四根弹簧连接而成的振动装置，弹簧的刚度系数分别为k 1和k 2。

假设质量为m 的物块A 沿倾角为α的斜面作平动，则该振动装置的固有频率ω =（ ）。

物理机械振动考试题及答案一、单项选择题（每题3分，共30分）1. 简谐运动的振动周期与振幅无关，与以下哪个因素有关？A. 质量B. 弹簧常数C. 初始位移D. 初始速度答案：B2. 阻尼振动中，振幅逐渐减小的原因是：A. 摩擦力B. 重力C. 弹力D. 空气阻力答案：A3. 以下哪个量描述了简谐运动的振动快慢？A. 振幅B. 周期C. 频率D. 相位答案：C4. 两个简谐运动的合成，以下哪个条件可以产生拍现象？A. 频率相同B. 频率不同C. 振幅相同D. 相位相反答案：B5. 以下哪个量是矢量？A. 位移B. 速度C. 加速度D. 以上都是答案：D6. 单摆的周期与以下哪个因素无关？A. 摆长B. 摆球质量C. 重力加速度D. 摆角答案：B7. 以下哪个量描述了简谐运动的能量？A. 振幅C. 频率D. 相位答案：A8. 以下哪个因素会影响单摆的周期？A. 摆长B. 摆球质量C. 摆角D. 重力加速度答案：A9. 阻尼振动中，振幅减小到原来的1/e时，经过的时间为：A. 1/2TB. TC. 2T答案：C10. 以下哪个现象不是简谐运动？A. 弹簧振子B. 单摆C. 弹簧振子的振幅逐渐减小D. 单摆的振幅逐渐减小答案：C二、填空题（每题4分，共20分）11. 简谐运动的周期公式为：T = 2π√(____/k)，其中m为质量，k为弹簧常数。

答案：m12. 单摆的周期公式为：T = 2π√(L/g)，其中L为摆长，g为重力加速度。

答案：L13. 阻尼振动的振幅公式为：A(t) = A0 * e^(-γt)，其中A0为初始振幅，γ为阻尼系数，t为时间。

答案：A014. 简谐运动的频率公式为：f = 1/T，其中T为周期。

答案：1/T15. 简谐运动的相位公式为：φ = ωt + φ0，其中ω为角频率，t 为时间，φ0为初始相位。

答案：ωt + φ0三、计算题（每题10分，共50分）16. 一个质量为2kg的物体，通过弹簧连接在墙上，弹簧的弹簧常数为100N/m。

航空机械考研试题及答案# 航空机械考研模拟试题一、单项选择题（每题2分，共20分）1. 航空发动机中，压气机的主要作用是（）。

A. 提供推力B. 压缩空气C. 冷却发动机D. 增加燃料效率答案：B2. 下列哪项不是航空材料的基本要求？（）A. 高强度B. 良好的塑性C. 耐高温D. 易腐蚀性答案：D3. 在航空器设计中，升力主要来源于（）。

A. 发动机推力B. 机翼的形状C. 机身的重量D. 尾翼的控制答案：B4. 航空机械系统中，液压系统主要用于（）。

A. 飞行控制系统B. 发动机点火C. 乘客座椅调节D. 燃料输送答案：A5. 航空器的静稳定性是指（）。

A. 飞机在无操纵下保持直线飞行的能力B. 飞机在遇到突风时的抗风能力C. 飞机在起飞时的稳定性D. 飞机在降落时的稳定性答案：A6. 航空发动机的推力与空气流量的关系是（）。

A. 正比B. 反比C. 无关D. 先增加后减少答案：A7. 航空器的气动中心位于（）。

A. 机翼的前缘B. 机翼的后缘C. 机翼的四分之一弦线处D. 机翼的中点答案：C8. 航空机械中，用于测量飞机速度的仪器是（）。

A. 空速表B. 姿态仪C. 罗盘D. 高度计答案：A9. 下列哪项不是航空发动机的主要组成部分？（）A. 进气道B. 燃烧室C. 涡轮D. 螺旋桨答案：D10. 在航空器的稳定性分析中，纵向稳定性主要取决于（）。

A. 机翼的面积B. 尾翼的面积C. 发动机的位置D. 机身的长度答案：B二、多项选择题（每题3分，共15分）11. 航空发动机的效率可以通过哪些因素提高？（）A. 增加压气机的压缩比B. 提高燃烧室的温度C. 减少发动机的重量D. 增加排气速度答案：ABC12. 航空器的结构设计需要考虑的因素包括（）。

A. 空气动力学B. 结构强度C. 材料成本D. 维护方便性答案：ABD13. 下列哪些因素会影响航空器的升力？（）A. 飞行速度B. 机翼的迎角C. 空气密度D. 机翼的重量答案：ABC14. 航空器的操纵系统包括哪些部分？（）A. 副翼B. 升降舵C. 油门控制D. 方向舵答案：ABD15. 航空机械中的液压系统可能存在的问题包括（）。

回想起去年这个时候，自己还在犹豫是不是要遵从自己的梦想，为了考研奋斗一次。

当初考虑犹豫了很久，想象过所有的可能性，但是最后还是决定放手一搏。

为什么呢？有一个重要的考量，那就是对知识的渴望，这话听来可能过于空洞吧，但事实却是如此。

大家也都可以看到，当今社会的局势，浮躁，变动，不稳定，所以我经常会陷入一种对未来的恐慌中，那如何消除这种恐慌，个人认为便是充实自己的内在，才不至于被一股股混乱的潮流倾翻。

而考研是一条相对比较便捷且回报明显的路，所以最终选择考研。

所幸的是结局很好，也算是没有白费自己将近一年的努力，没有让自己浑浑噩噩的度过大学。

在准备备考的时候，我根据自己的学习习惯，做了一份复习时间规划。

并且要求自己严格按照计划进行复习。

给大家一个小的建议，大家复习的时候一定要踏踏实实的打好我们的基础，复习比较晚的同学也不要觉得时间不够，因为最后的成绩不在于你复习了多少遍，而是在于你复习的效率有多高，所以在复习的时候一定要坚持，调整好心态，保证自己每天都能够有一个好的学习状态，不要让任何事情影响到你，做好自己！在此提醒大家，本文篇幅较长，因为想讲的话实在蛮多的，全部是我这一年奋战过程中的想法、经验以及走过的弯路，希望大家看完可以有所帮助。

最后结尾处会有我在备考中收集到的详细资料，可供各位下载，请大家耐心阅读。

南京航空航天大学精密驱动与振动利用的初试科目为：(101)思想政治理论(201)英语一(301)数学一和(816)材料力学或(823)电工电子学参考书目为：1.《材料力学（上、下册）》（第五版），刘鸿文.高等教育出版社关于英语复习的一些小方法英语就是平时一定要做真题，把真题阅读里面不会的单词查出来，总结到笔记上，背诵单词，在考试之前，可以不用大块的时间，但一定要每天都看最起码2小时英语，把英语当做日常的任务，真题一定要做，而且单词要背熟，我在考试之前背了3遍的考研单词，作文可以背诵一些好词好句，在考场灵活运用。

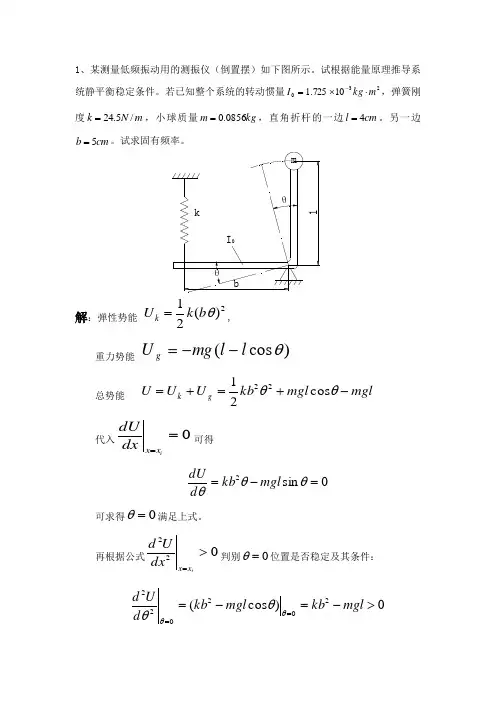
1、某测量低频振动用的测振仪（倒置摆）如下图所示。

试根据能量原理推导系统静平衡稳定条件。

若已知整个系统的转动惯量23010725.1m kg I ⋅⨯=-，弹簧刚度m N k /5.24=，小球质量kg m 0856.0=，直角折杆的一边cm l 4=。

另一边cm b 5=。

试求固有频率。

kblθθI 0m解：弹性势能 2)(21θb k U k =,重力势能)cos (θl l mg U g --=总势能 m g l m g l kb U U U g k -+=+=θθcos 2122 代入0==ix x dxdU 可得0sin 2=-=θθθmgl kb d dU可求得0=θ满足上式。

再根据公式022>=ix x dx Ud 判别0=θ位置是否稳定及其条件：0)cos (202022>-=-===mgl kb mgl kb d U d θθθθ即满足mgl kb>2条件时，振动系统方可在0=θ位置附近作微幅振动。

系统的动能为 2210θ∙=I T代入0)(=+dtU T d 可得 0sin 20=-+∙∙θθθmgl kb I由0=θ为稳定位置，则在微振动时0sin ≈θ，可得线性振动方程为：0)(20=-+∙∙θθmgl kb I固有频率2I mglkb p -=代入已知数据，可得)/(410725.104.081.90856.005.05.2432s rad p =⨯⨯⨯-⨯=-2、用能量法解此题：一个质量为均匀半圆柱体在水平面上做无滑动的往复滚动，如上图所示，设圆柱体半径为R ，重心在c 点,oc=r,，物体对重心的回转体半径为L，试导出运动微分方程。

解：如图所示，在任意角度θ（t ）时，重心c 的升高量为∆=r （1－cos θ）=2rsin 22θ取重心c 的最低位置为势能零点，并进行线性化处理，则柱体势能为 V=mg ∆=2mg r sin22θ ≈21mgr 2θ （a ）I b =I c +m bc 2=m(L 2+bc 2) （b ）bc 2=r 2+R 2-2rRcos θ(t) （c ）而柱体的动能为 T=21I b ∙θ2把（b ）式，（c ）式两式代入，并线性化有T=21m[L 2＋（R －r ）2]∙θ2（d ）根据能量守恒定理，有21m[L 2＋（R －r ）2]∙θ2＋21mgr 2θ=E=const 对上式求导并化简，得运动微分方程为[L 2＋（R －r ）2]∙∙θ＋gr θ=0 （e ）3、一质量为m 、转动惯量为I 的圆柱体作自由纯滚动，圆心受到一弹簧k 约束，如图所示，求系统的固有频率。

2007年振动力学期末考试解答第一题（20分）1、物块M 质量为m 1。

滑轮A 与滚子B 的半径相等，可看作质量均为m2、半径均为r 的匀质圆盘。

斜面和弹簧的轴线均与水平面夹角为β，弹簧的刚度系数为k 。

又m 1 g >m 2 g sin β , 滚子B 作纯滚动。

试用能量法求：（1）系统的微分方程；（2）系统的振动周期。

2、在图示系统中，质量为m 1、半径为R 的匀质圆盘，可沿水平面作纯滚动。

质量不计的水平直杆AB 用铰链A 、B 分别与圆盘A 、匀质直杆BC 连接。

杆BC 长为L ，质量为m 2，在B 连接一刚度系数为k 的水平弹簧。

在图示的系统平衡位置时，弹簧具有原长。

试用能量法求：（1）系统的微振动的运动微分方程；（2）系统的微振动周期。

解1：系统可以简化成单自由度振动系统，以滚子B 的轮心位移x 作为系统的广义坐标，在静平衡位置时 x ＝0，此时系统的势能为零。

系统动能和势能为：2212222222221)2(21]))(21(2121[))(21(2121x m m r x r m x m r x r m x m T +=+++=221kx V =在理想约束的情况下，作用在系统上的主动力为有势力，则系统的机械能守恒，则有：E kx xm m =++222121)2(21 上式两边对t 求导整理得动力学方程为：0221=++x m m kx振动周期为：km m T 2102π2π2+==ω 解2：系统可以简化成单自由度振动系统，以匀质轮轮心A 的位移x 作为系统的广义坐标，在静平衡位置时x ＝0，此时系统的势能为零。

系统动能和势能为：221221222)3123(21)(2321)(3121xm m R x R m L x L m T +=+=2221)]cos(1[21kx L x gL m V +--=在理想约束的情况下，作用在系统上的主动力为有势力，则系统的机械能守恒，则有：E kx L x gL m xm m V T =+--+=+2222121)]cos(1[21)3123(21 上式两边对t 求导，得：0)sin(21)3123(221=+-+kx LxgL m xm m 取LxL x≈)sin(，则系统的微分方程为： 0312321212=+-+x m m gm k x 固有频率为：2120312321m m gm k +-=ω 振动周期为：π2ω=T第二题（20分）在图示振动系统中，已知：物块的质量为m ，两弹簧的刚度系数分别为k 1、k 2 ，有关尺寸L 、b 已知，不计杆重。

物理机械振动考试题及答案一、选择题1. 简谐振动的频率与振幅无关，这是由什么决定的？A. 振子的质量B. 振子的弹性系数C. 振子的阻尼D. 振子的初始条件答案：B2. 在阻尼振动中，振幅随时间如何变化？A. 保持不变B. 逐渐减小C. 逐渐增大D. 先增大后减小答案：B3. 以下哪个不是简谐振动的特点？A. 周期性B. 振幅不变C. 频率恒定D. 振子质量不变答案：D4. 什么是共振现象？A. 振子的振动频率等于系统固有频率时的现象B. 振子的振幅达到最大时的现象C. 振子的振动频率等于外部驱动频率时的现象D. 振子的振动频率等于外部阻尼频率时的现象答案：A5. 以下哪个公式描述了简谐振动的位移？A. \( x = A \sin(\omega t + \phi) \)B. \( x = A \cos(\omega t + \phi) \)C. \( x = A \tan(\omega t + \phi) \)D. \( x = A \sec(\omega t + \phi) \)答案：B二、填空题6. 一个物体在水平面上做简谐振动，其振动周期 \( T \) 与振动频率 \( f \) 的关系是 \[ T = \frac{1}{f} \]。

7. 阻尼振动中，振幅随时间的衰减速度与振子的________成正比。

8. 共振现象中，振子的振动频率等于系统的________频率。

9. 简谐振动的位移公式中，\( \omega \) 表示________，\( \phi \) 表示________。

10. 阻尼振动的振幅随时间的衰减可以表示为 \( A(t) = A_0 e^{-\alpha t} \)，其中 \( \alpha \) 表示________。

三、简答题11. 简述什么是阻尼振动，并说明其振幅随时间的变化趋势。

答案：阻尼振动是指在振动过程中，由于存在阻力（如空气阻力、摩擦力等），振子的振动能量逐渐减小，导致振幅逐渐减小的振动。

南京市《机械振动》测试题(含答案)一、机械振动 选择题1．如图所示为某物体系统做受迫振动的振幅A 随驱动力频率f 的变化关系图，则下列说法正确的是A ．物体系统的固有频率为f 0B ．当驱动力频率为f 0时，物体系统会发生共振现象C ．物体系统振动的频率由驱动力频率和物体系统的固有频率共同决定D ．驱动力频率越大，物体系统的振幅越大2．用图甲所示的装置可以测量物体做匀加速直线运动的加速度，用装有墨水的小漏斗和细线做成单摆，水平纸带中央的虚线在单摆平衡位置的正下方。

物体带动纸带一起向左运动时，让单摆小幅度前后摆动，于是在纸带上留下如图所示的径迹。

图乙为某次实验中获得的纸带的俯视图，径迹与中央虚线的交点分别为A 、B 、C 、D ，用刻度尺测出A 、B 间的距离为x 1；C 、D 间的距离为x 2。

已知单摆的摆长为L ，重力加速度为g ，则此次实验中测得的物体的加速度为（ ）A ．212()x x g L π-B ．212()2x x g L π-C ．212()4x x g L π-D ．212()8x x g Lπ- 3．如图所示，将小球甲、乙、丙（都可视为质点）分别从A 、B 、C 三点由静止同时释放，最后都到达竖直面内圆弧的最低点D ，其中甲是从圆心A 出发做自由落体运动，乙沿弦轨道从一端B 到达最低点D ，丙沿圆弧轨道从C 点运动到D ，且C 点很靠近D 点，如果忽略一切摩擦阻力，那么下列判断正确的是（ ）A ．丙球最先到达D 点，乙球最后到达D 点B ．甲球最先到达D 点，乙球最后到达D 点C ．甲球最先到达D 点，丙球最后到达D 点D ．甲球最先到达D 点，无法判断哪个球最后到达D 点4．如图所示，弹簧下面挂一质量为m 的物体，物体在竖直方向上做振幅为A 的简谐运动，当物体振动到最高点时，弹簧正好处于原长，弹簧在弹性限度内，则物体在振动过程中A ．弹簧的弹性势能和物体动能总和不变B ．物体在最低点时的加速度大小应为2gC ．物体在最低点时所受弹簧的弹力大小应为mgD ．弹簧的最大弹性势能等于2mgA5．如图所示是扬声器纸盆中心做简谐运动的振动图象，下列判断正确的是A ．t =2×10-3s 时刻纸盆中心的速度最大B ．t =3×10-3s 时刻纸盆中心的加速度最大C ．在0〜l×10-3s 之间纸盆中心的速度方向与加速度方向相同D ．纸盆中心做简谐运动的方程为x =1.5×10-4cos50πt （m ）6．如图1所示，轻弹簧上端固定，下端悬吊一个钢球，把钢球从平衡位置向下拉下一段距离A ，由静止释放。

《机械振动学》课程习题库第一章1.1 何谓机械振动？表示物体运动特征的物理量有哪些？ 1.2 按产生振动的原因分为几类？按振动的规律分为几类？ 1.3 何谓线性系统、机械系统和等效系统？1.4 如何理解瞬态振动、稳态振动、自由振动、强迫振动、纵向振动。

横向振动、扭转振动、参数振动和非线性振动？1.5 写出频率、角频率、相位、幅值、有阻尼固有频率，并说明意义，注明单位值。

1.6 如何理解粘性阻尼系数、等效阻尼、临界阻尼系数、欠阻尼和过阻尼？ 1.7 振动对机械产品有哪些影响？1.8 利用振动原理而工作的机电设备有哪些？试举例说明。

1.9 重温非简谐的周期性振动傅里叶级数，时间函数为f(t)，其周期为T ，表达式为：)s i n c o s ()(10t n b t n an a t f n n ωω++=⎰∞=式中：⎰=Tdt t f Ta 00)(1⎰=Tn tdt n t f T a 0cos )(2ω⎰=Tn tdt n t f T b 0sin )(2ω 注：《手册》P91.10将下图所示的f(t)展成傅立叶级数。

参考答案：()∑∞===5.2.1sin 1440t np t f n pb n b n n n ωππ傅氏级数为奇数时，，当为偶数时，当 f(t)P 0 -Pπ/ω2π/ω 3π/ω 4π/ωt1.11今有一简谐位移x(t)(mm)，其表达式为：()=8sin(24 -),3x t t π求：1. 振动的频率和周期；2. 最大位移、最大速度和最大加速度；3. t=0时的位移、速度和加速度；4. t=1.5s 时的位移、速度和加速度。

参考答案：24rad/s ，3.82Hz ，0.2618s ；192mm/s ，4608mm/s 2；-6.9282mm ，96mm/s ，3990.65 mm/s 2 ；-3.253mm ，175.4mm/s ，1874 mm/s 21.12一振动体作频率为50Hz 的简谐振动，测得其加速度为80 m/s 2 ，求它的位移幅值和速度幅值。

南航机械原理考研真题及答案解析机械原理是航空工程领域中的重要科目之一，在南京航空航天大学等高校的机械工程专业中也是必修课程。

考研是每一位研究生学子都要面对的挑战，备考机械原理是他们获得成功的关键之一。

本文将针对南航机械原理的考研真题及答案进行解析，帮助广大考生更好地备考。

第一题：某飞机之重心远离机翼强度宽度的中心线y距离0.3m，飞行速度27m/s,气流密度ρ=1kg/m³，假设升力矩动臂为a=2m，求主翼升力动臂b。

解析：题目给出了飞机重心远离机翼强度宽度的中心线的距离，即y=0.3m，飞行速度为27m/s，气流密度为1kg/m³，升力矩动臂a=2m，要求解主翼升力动臂b。

根据机械原理的知识可以得知，主翼升力动臂b与重心距离x的关系为：b=a+cy其中，c为气动力矩（升力矩）和质量力矩之比。

现在需要计算c的值。

根据所给数据，飞行速度为27m/s，气流密度为1kg/m³时，可以利用公式c=0.5ρv²SC / (Mga) 求得：c=0.5*1*27²*2/9.8接下来带入数值进行计算：c≈0.5*1*729*2/9.8c≈74.4898继续求解主翼升力动臂b：b=a+cyb=2+74.4898*0.3b≈23.3479所以，主翼升力动臂b≈23.3479。

第二题：一弹簧的两端分别连接质量为m1和m2的两个物体，质量m1=2kg，质量m2=4kg，现已知在重力的作用下两物体保持了静止。

若将两物体看作质点，弹簧初始未变形时，求弹簧的劲度系数。

解析：题目中给出了两个具有质量的物体，质量分别为m1=2kg 和m2=4kg，并且在重力作用下保持静止。

要求解弹簧的劲度系数。

根据机械原理的知识可以得知，弹簧的等效质量m'等于两个物体的质量之和，即m'=m1+m2=2kg+4kg=6kg。

由于受力平衡，所以弹簧受力也为零。

所以弹簧的劲度系数k与物体的质量和等效质量的关系为：k=mg/m'其中，g为重力加速度, m为物体的质量之和。