中考化简求值题专项练习及答案(20210306053909)

中考数学化简求值专项训练注意：此类题目的要求，如果没有化简，直接代入求值一分不得！ ！考点：①分式的加减乘除运算（注意去括号，添括号时要变号，分子相减时要看做整体）②因式分解（十字相乘法，完全平方式，平方差公式，提公因式） ③二次根式的简单计算（分母有理化，一定要是最简根式）类型一：化简之后直接带值，有两种基本形式：1. 含根式，这类带值需要对分母进行有理化，一定要保证最后算出的值是最简根式2. 常规形，不含根式，化简之后直接带值m 22m 1m 11. 化简，求值：21(m 1） , 其中 m= 3 ．m m12. 化简，求值：1 · x 36x 29x 1 x，其中 x ＝－ 6．x3 x 2 2x 2 x1 12x ，其中 x1 ， y 23. 化简，求值：x yx 2 2 xy y 2 x yx 2 2x 2x ( x 2) ，其中 x14. 化简，求值：24x 2.x25. 化简，求值： (11 ) ÷ x2 x 2 2x 1 ，其中 x=2x16. 化简，求值：x 2 4 x 2x3 ． x 24x 4x x ，其中 x127. 化简，求值：2 a 24 a 2，其中 a5 ．a6a 9 2a68. 化简，求值： (3xx ) x 2，其中x3 x 1x 1 x 21 2类型二：带值的数需要计算，含有其它的知识点，相对第一种，这类型要稍微难点1. 含有三角函数的计算。

需要注意三角函数特殊角所对应的值. 需要识记，熟悉三角函数例题x22x 1 11.化简，再求代数式的值，其中 x=tan60 x 2 -tan451x 12. 先化简 (11 )2 ，其中 x2 （tan45 ° -cos30 °）224x 42x 2 x x x2x3. (11 )2 ，其中 x2 （tan45 ° -cos30 °）224x 42x 2x x x2x2. 带值为一个式子，注意全面性，切记不要带一半。

完整word版)中考数学化简求值专项训练中考数学化简求值专项训练注意：此类题目的要求是化简之后再代入求值，直接代入求值不得分。

考点包括分式的加减乘除运算（注意去括号，添括号时要变号，分子相减时要看做整体）、因式分解（十字相乘法、完全平方式、平方差公式、提公因式）以及二次根式的简单计算（分母有理化，一定要是最简根式）。

类型一：化简之后直接带值，有两种基本形式：1.含根式，这类带值需要对分母进行有理化，一定要保证最后算出的值是最简根式。

例如，化简并求值：$\frac{m^2-2m+1}{m-1-\frac{1}{m+1}}$，其中$m=3$。

解：先化简分母，得到$\frac{m^2-1}{m^2-1}$，然后将分子分母同时化简，得到$\frac{(m-1)^2}{m}$。

代入$m=3$，得到$\frac{4}{3}$。

2.常规形，不含根式，化简之后直接带值。

例如，化简并求值：$\frac{x^3-6x^2+9x-1}{x^2-3x}$，其中$x=-6$。

解：先化简，得到$\frac{(x-3)^2}{x(x-3)}$。

代入$x=-6$，得到$\frac{1}{6}$。

3.化简并求值：$\frac{11+2x}{x-y}$，其中$x=1$，$y=-2$。

解：先化简，得到$\frac{11+2x}{x-y}=\frac{13}{3}$。

代入$x=1$，$y=-2$，得到$\frac{13}{3}$。

4.化简并求值：$\frac{x^2-2x}{2x-4}+\frac{2}{x+2}$，其中$x=0.5$。

解：先化简，得到$\frac{x(x-2)}{2(x-2)}+\frac{2}{x+2}=\frac{x}{2}+\frac{1}{x+2}$。

代入$x=0.5$，得到$\frac{5}{4}$。

5.化简并求值：$\frac{1-x}{2x}+\frac{2x}{x^2-4x+3}$，其中$x=2$。

解：先化简，得到$\frac{1}{2}-\frac{2x-3}{x-1}\cdot\frac{1}{x-3}=\frac{5}{6}$。

专项辅导（4）化简求值题及答案化简求值题在中考数学中占有十分重要的地位，纵观近几年河南省的 中考数学试题，都出现了此类题目，所占分值为8分，可见此类题目的重 要性!在难度上化简求值题并不难，侧重于对基础知识的考查•进行适（2008.河南）1.先化简再求值:C 或A B C 的形式,请你从中任选一种进行计算，先化简再求值其中x 3.当的练习能够对此类题目更好的掌握 ，在考试中不至于失分a 1 aa 1 a 22a 1 1 — 丄，其中a 12.a（2009.河南）2.先化简「，然后从2,1,1中选取一个合适的数作为 x 的值代入求值.（2010.河南）3.已知A2，B 4，C，将它们组合成围内选取一个合适的整数作为 X 的值代入求值.以下题目选取的是九年级上册数学中的化简求值题 •请认真完成!分别为x 3 2,y 32（2011河南）4.先化简1X 2 4x 4然后从-2< X < 2的范围内选取一个合适的整数作为 X 的值代入求值.（2012.河南）5.先化简x 2 4x 4 2 -x 2x-,然后从 5V X V 5的范X6•先化简,再求值:2y X 2 2xy y 2其中x,y 的值x 18.先化简，再求值：x 11 —,其中x 2.1 x 1x 2 2x9.先化简,再求值x 2 3y 4y 4 xyx 其中x y 的勺值 ・ 22x ,其中x, y 的值x4xy 4yx 2yx <21分别为—y <2 17•先化简,再求值：12a 1,其中a3 210.（2009.安顺）先化简，再求值:x 2 4x 4 2x 4(x2）,其中x 5.a2- 4a24a 4 2 - a）2a22a，其中a是方程2 Q 11.（2009威海）先化简，再求值：a b a b 2a b 3a ,其中a 2 . 3,b3 2.市中考题）<a 113.先化间a 1121,然后再选取一个合适的值作为a的值代a a入求值.14.已知x 2 1, y , 2 1,求一—的值.y x12.先化简，再求值: 亍，其中x 21.（乐山115.先化简，再求值:（X2+3X+1=0的根.1 1 2y 16.（平顶山中考模拟）先化简，再求值：2 2,其X y X y X y中X 2010 2,y2,小明做这道题时，把X 2010 2抄成X 2001 2,计算结果仍正确，请你通过计算说明原因.17.（2005河南）已知X 、21,求X 118.（2003河南）已知X 13 2 2，y3—2—2'求:x 4的值- 19.以后还有总的训练2012.11.15以下为补充题目：20.（2013.河南）先化简，再求值：X 2 2 2x 1 2x 1 4x xx ,2 .21.（2014河南）先化简，再求值：匚」 2 - 1，其中x 2X X X2 2a 2ab - (1 1),其中a 5 2a 2b b a22.(2015河南)先化简，再求值:223.（2013许昌一模）先化简，再求值：电二a 4丄，然后选择一个a 3 2a 6 a 2你喜欢的数代入求值.24.（2015郑州外国语三模）先化简再求值：上12a a，其中a 1 a a 2a 1a 2 a 20.25.（2015郑州外国语月考）先化简再求值：1 1-其中x xx ■ 27 3tan 60 2cos45 .226. （2015郑州市九年级一模）先化简笃卫x26x 9丄,再取恰x 1 x 2x 1 x 1 当的x的值代入求值.27. （2015郑州市九年级二模）先化简-x 1 1，再从2x3x 1 x 1中选一个合适的整数代入求值.28. （2015平顶山一模）先化简，再求代数式筈二的值，其中x y x yx 2 cos45 2, y 2.29.（2014新乡二模）先化简，再求值: a2 4a 4 a2 2a1 ,其中a是一元二次方程x2 4x 7 0的一个根.30.（2015.洛阳一模）先化简，再求值:a a 23，其中a 满a 2足a2 a 2 0.31.（2014贺州）先化简，再求值:a2b ab a2 2a -其中a.3 1 ,b -3 1.32.（2014.泰州）先化简，再求值:1,其中x满足33.（2015湖南岳阳）先化简，再求值：12xx2 4x 4x ，其中x34.（2014苏州）先化简，再求值:xx2 1，其中x35. （2015.山东德州）先化简,再求值:- - a 2ab b ,其中a aa 2 ..3,b 2 336. （2014.凉山州）先化简，再求值:胃3 a 2 丄,其中a满足3a 6a a 2a2 3a 1 02 237. （2014宁夏）先化简，再求值：—b a°,其中a 1 .3,a b a b a bb 1 -3 .38. （2013遵义）已知实数a 满足a 2 2a 15 o ,求代数式丄 二2a 1 a 139.（2014泉州）先化简，再求值：a 2 2 a a 4 ,其中a .3 .40.（2013曲靖改）先化简再求值：2x ： 2x2X X X，其中x 1 x 2x 1 x 1x 12 .2015.10.6a 1 a a 2 2a的值.专项辅导（4）化简求值题参考答案• 1.解：a 1a a2a 1a 1a 1 2 a21 a2a 1 21原式• 2.解:x2x2 2 x 1x 1 x 121 x原式2妊注意:这里xx 2 x2 4 x 2x 2 2 x 2x 2 x 2 xx x 2x 2 x 2 x1x 2当x 3时原式 1 13 2或解：A B C1 2 xx 2 x 2 4 x 21 2 x 2x 2 x 2 x 2 x1 2x 2 x x 2x 2x x 21x当x 3时原式 13注意:对于两种选择要注意运算顺序1 x2 4x 4• 4.!： 1 2x 1 x 1 x 1 1 x 1 x 1x 1 x 2 2• 3.解：A1 2 xB Cx 1 x 2x 1x 2当x 0时原式「丄0 2 2或当x 2时原式注意：为保证本题中所有分式都有意义,x只能取0或2.• 5.解: x2 4x 4 x2 2xx 2 2X2 4x x 2 x2x 2 xx x 2 x 2 x 21x 2,5 x ,5,且x为整数•••若使分式有意义,x只能取1和1 当x 1时1原式 - 11 2（或当x 1时原式1 1）1 2 3• 6.解：」12空一2x y x y x 2xy yx y x yx yx y2yx y2yx yx yx原式..32.32“ 2.6• 7•解：1aaaaa原式.2,y 3 (2)时.3<2aa2 2a1 1丄1a1 a132a 1a12• 8.解：-x 1 x212x 1x 1 x 1 1 x 1x 1 x2x X 1x 1 x2 2 2 2 2a 2ab b 2a ab b 3aab当 a 2 , 3,b .. 3 2 时x 2 x 2原式 原式.32 22 3• 9•解：xy 4y22x 4xy 4y 4xy x 2y2y x 2y x 2y 4xy x 2xy 2 -x 2y x 2yy x 2y x x 2y x 2y x 2y xy x .2 1 y 2 1 • ••原式 2 1 .2 1• 10 解:2x 4x42x 4• 12.解:x x 2 x 2 x 2 1 x当x 2 1时原式1站2 172 12 12 1当x 、2时•13.解 :其a由题意可知：a 1 当a 4时 原式 .4 2 • 14 解：••• x .21, y.2 1/. x y 2 1 .. 2 1 2... 2 xy. 2 1.2 1 2 11• x y2 2x yy xxy2x y2xyxy—22 2 2 118 26• 15 解:a 24 1 22a 4a 42 aa 2 2a程,应根据题目化简结果的特点 ，选择合适的处理方法，如本题可以考虑整体 思想采用整体代入的方法.2• 16.解：」2 32^x y x y x y x y x2?2y 3原式因为化简结果里面没有 x ,所以本 题的计算结果与x 的取值无关,从而小 明在抄错x 值的情况下所得结果依然a 2 a 2 1 2a 22 a 2 a a 2 a 21a a 2a 2 a 2 2a 3 a a 2 a 2 2正确. • 17.解:x 12 小a 3a2••• a是方程x2 3x 1 0的根・ 2• • a3a 1 0原式・ 2• • a3a 1原式 1 12 2注意:对于此类题目，先不要急于解方• 18解：x13 2 2 3 2j23 2迈 3 2/23 229 8 3 2 2xy62 6 1 1 36 6 30• 19.以后还有总的训练以下为补充题目 • 20 解：1 x 1当x21时原式11 2 2 11222• 22.解:a2ab b 2（-丄）2a 2bb aa b 2a b2 a b aba b ab2 a bab2当a .5 1,b ,5 1时原式51 5125 122• 23.解:—2a 245a 32a 6a 2a 2 2 a 35 a 3 a 2 a 2 a 225a 2 a 23a 2当a 1时原式311 2注意:本题,a2,a3.y13 2 •一23 2.2 x y 3 2、2 3 2 .. 2 6 xy3 2 ..2 3 2、、2 982x y. 4xy 4xy y xxyx2y 6xy1x 2 2 2x1 2x4x 2 1 4x 1 4x 22x 2 x 4x 4 3当x•、2时原式■— 223 2 3 5 2x• 21 解：- 1 —2 x 21xxxx 1 x 1 2x x 21x x 1xx1xx 12x1x4x22• 24 解:a 2 2a 12a a 1a 12_aT a 2 a 22x 3 x 1 1x 1 x 1 x 3 x 1x 1 1 x 1 x 3 x 1x 1 x 3 x1 x 32 x 1 x1 x 3a 11, a 22•/a 1 0,a 1 • a 2 •原式 1 • 25 解：1 — x 2x 1 x x x 1 x 1 1 x 1x .27 3tan 60 2 cos45•原式 耘 12 1「2 1• 26 解: x 3 x 21x 26x 9x 2 2x 1 x 3・・ 2 ・x 1 0,x1 0, x 3 0, x 1 i• x1,x3当x 0时原式2 20 33x2•27■解 ：x 211 1 x 1x 2 x 1 1x 1 x 1x 1x 2 x 1 x 1 x 1xxx 12・x 1 0,x1 0,x 0• x1,且x 0•在 2 x3中,x 可取的整数只有2当x 2时原式2 22 132• 28.解:电一电电yx y x y3x 2 y 2x y2 2x yx yx y x y1x yx 2cos45 2 2 — 2 2 .22 当x 2 ,2,y 2 时原式1 2.22• 29 解:a 1a24a 4a 2a22aa 1 a 2 4 aa 2 2a a 2 aa a 1 a 2 a 2 aa a 2 4 a••• a是一元二次方程x2 4x 7 0 的一个根4a 7 02a 4a 411a 2 211• 30 解：a2 a 2a 1 a2 4 3a 2 a 2“ 2a 2a 1a 2 a 1 a 1a 1a 12 a a 2 0解之得:a1 2, a24■/ a 1 0,a 1• a2当a 2时原式 2 1 32 1• 31.解:a2b aba22a 1a 1abab原式,3• 32.解:1,b .3..3x2 2xx 2 x 1 x 1x 1 x x 2 xx 2 x 1 x 1xx ---------2ab 2a 22ab b 2aaa b a baa2a ba ba b当a2 ..3,b 2.. 3 时原式 2 3 2 34 2 3 丿原式 J2 、3 23 2、332a 3 a 4 53a a 2 a 2 a 3a 2 *• 33 解:2x xx 24x 4 • 36.解:3a 2 3 6a原式 、2 2 、2 • 34 解: 3a a 31 3 a2 3a2・a 3a 1・ 2• • a3a 1 原式13 11 013x x 2 1 • 37.解:a 2原式 2 112 b2• 35 解： -----------2ab b 2aa a bba b a ba b a b a 2 b 2 a b a b a b a b a 2 b 2 1 a b当a 1 J 3, b 1 品时原式1 x2 2 22111 a2 a 1 a 1 a 1 1 a 1 a 1 a 1 2T a 2 2a 15••• a 1 216原式-116 82• 39解: a 2 a a 4 a 2 4a 4 a 2 4a 2a 2 4 当a . 3时 原式 2.3 2 4 6 4102 2• 40解：竺2xx_「亠x 1 x 2x 1 x 12x x 1 x 1 x 1 2x x x 1 x 1 x x 1 x 1 x x 12原式1.31 、3• 38 解:a 2 a 21a 1 a 2 a 2 2a 1原式1 ,2 1 2 2 1 \2 1 、、22015.10.6 星期二15:36x x 1 x 1 x 1 xX 1 x11 x2 42当x ,5时原式• 11 解：a b 2 a b 2a b 3a2。

中考数学化简求值专项训练中考数学化简求值专项训练注意：此类题目的要求是化简后再求值，直接代入求值一分不得！考点包括分式的加减乘除运算（注意去括号，添括号时要变号，分子相减时要看做整体）、因式分解（十字相乘法、完全平方式、平方差公式、提公因式）、二次根式的简单计算（分母有理化，一定要是最简根式）。

类型一：化简之后直接带值，有两种基本形式：1.含根式，这类带值需要对分母进行有理化，一定要保证最后算出的值是最简根式。

例如：化简，求值：$\frac{m^2-2m+1}{m-1-\frac{1}{m+1}}$，其中$m=3$。

解：将分母有理化，得到$\frac{m^2-2m+1}{\frac{m^2-1}{m+1}-1}$，化简后得到$\frac{2(m+1)}{m}$，带入$m=3$，得到答案为$2\frac{2}{3}$。

2.常规形，不含根式，化简之后直接带值。

例如：化简，求值：$\frac{x^3-6x^2+9x-1}{x^2-2x-1}$，其中$x=-6$。

解：将分子因式分解，得到$(x-1)^2(x-1)$，将分母因式分解，得到$(x-1)^2$，化简后得到$x-1$，带入$x=-6$，得到答案为$-7$。

3.化简，求值：$\frac{11x}{x-y}+\frac{3}{x^2+2xy+y^2}$，其中$x=1$，$y=-2$。

解：将第一项分子分母同时乘以$x-y$，得到$\frac{11x(x-y)+3(x-y)}{(x-y)(x^2+2xy+y^2)}$，化简后得到$\frac{11x+3}{x+2y}$，带入$x=1$，$y=-2$，得到答案为$1$。

4.化简，求值：$\frac{2x-4}{x^2-2x+11}$，其中$x=1$。

解：将分子因式分解，得到$2(x-2)$，将分母化简，得到$(x-1)^2+10$，化简后得到$\frac{2}{9}$，带入$x=1$，得到答案为$\frac{2}{9}$。

本文部分内容来自网络，本人不为其真实性负责，如有异议请及时联系，本人将予以删除数学中考化简求值专项练习题注意：此类要求的题目，如果没有化简，直接代入求值一分不得！ 考点：①分式的加减乘除运算 ②因式分解 ③二次根式的简单计算1.化简，求值：111(11222+---÷-+-m m m m m m ）, 其中m =3．2.先化简，再求代数式2221111x x x x -+---的值，其中x=tan600-tan4503.化简：xx x x x x x x x 416)44122(2222+-÷+----+, 其中22+=x4.计算：332141222+-+÷⎪⎭⎫ ⎝⎛---+a a a a a a a ．5.6、先化简，再求值：13x -·32269122x x x xx x x-+----，其中x ＝－6．7.先化简：再求值：⎝⎛⎭⎫1－1a －1÷a 2－4a ＋4a 2－a ，其中a ＝2＋ 2 .8.先化简，再求值：a －1a ＋2·a 2＋2a a 2－2a ＋1÷1a 2－1，其中a 为整数且－3＜a ＜2.9.先化简，再求值：222211y xy x xy x y x ++÷⎪⎪⎭⎫ ⎝⎛++-，其中1=x ，2-=y ．10.先化简，再求值：2222(2)42x x x x x x -÷++-+，其中12x =.11.先化简，再求值：222112()2442x x x x x x-÷--+-，其中2x =（tan45°-cos30°）12.22221(1)121a a a a a a +-÷+---+．13.先化简再求值：1112421222-÷+--•+-a a a a a a ，其中a 满足20a a -=．14.先化简：144)113(2++-÷+-+a a a a a ，并从0，1-，2中选一个合适的数作为a 的值代入求值。

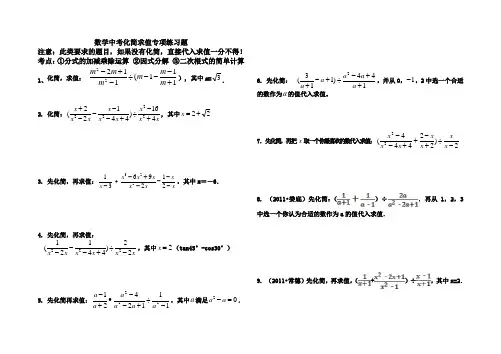
数学中考化简求值专项练习题注意：此类要求的题目，如果没有化简，直接代入求值一分不得！ 考点：①分式的加减乘除运算 ②因式分解 ③二次根式的简单计算1、化简，求值： 111(11222+---÷-+-m m m m m m ）, 其中m =3．2. 化简：xx x x x x x x x 416)44122(2222+-÷+----+, 其中22+=x3. 先化简，再求值：13x -·32269122x x x xx x x-+----，其中x ＝－6．4. 先化简，再求值：222112()2442x x x x x x-÷--+-，其中2x =（tan45°-cos30°）5. 先化简再求值：1112421222-÷+--•+-a a a a a a ，其中a 满足20a a -=．6. 先化简：144)113(2++-÷+-+a a a a a ，并从0，1-，2中选一个合适的数作为a 的值代入求值。

7. 先化简，再把 x 取一个你最喜欢的数代入求值：2)22444(22-÷+-++--x xx x x x x8. （2011•娄底）先化简：（）÷．再从1，2，3中选一个你认为合适的数作为a 的值代入求值．9. （2011•常德）先化简，再求值，（+）÷，其中x=2．10. （2011•遵义）先化简，再求值：，其中x=2，y=﹣1．11. （2011•泸州）先化简，再求值：，其中．12. （2011•曲靖）先化简，再求值：，其中a=．。

化简求值专项练习题1．先化简，再求值：2（3a2﹣ab）﹣3（2a2﹣ab），其中a=﹣2，b=3．2．先化简，再求值：6a2b﹣（﹣3a2b+5ab2）﹣2（5a2b﹣3ab2），其中a=﹣2，b=．3．先化简，再求值：3x2y2﹣[5xy2﹣（4xy2﹣3）+2x2y2]，其中x=﹣3，y=2．4．先化简，再求值：5ab2+3a2b﹣3（a2b﹣ab2），其中a=2，b=﹣1．5．先化简，再求值：2x2﹣y2+（2y2﹣x2）﹣3（x2+2y2），其中x=3，y=﹣2．6．先化简，再求值：5x2﹣[x2+（5x2﹣2x）﹣2（x2﹣3x）]，其中x=．7．先化简，再求值：（6a2﹣6ab﹣12b2）﹣3（2a2﹣4b2），其中a=﹣，b=﹣8．8．先化简，再求值：x2y﹣（2xy﹣x2y）+xy，其中x=﹣1，y=﹣2．9．先化简，再求值：5（xy+3x2﹣2y）﹣3（xy+5x2﹣2y），其中x=，y=﹣1．10．当|a|=3，b=a﹣2时，化简代数式1﹣{a﹣b﹣[a﹣（b﹣a）+b]}后，再求这个代数式的值．11．先化简，再求值：a2﹣（2a2+2ab﹣b2）+（a2﹣ab﹣b2），其中a=3，b=﹣2．12．先化简，再求值：3a2﹣（2ab+b2）+（﹣a2+ab+2b2），其中a=﹣1，b=2．13．先化简再求值，已知a=﹣2，b=﹣1，c=3，求代数式5abc﹣2a2b﹣[（4ab2﹣a2b）﹣3abc]的值．14．先化简，再求值：﹣2（ab﹣3a2）﹣[a2﹣5（ab﹣a2）+6ab]，其中a=2，b=﹣3．15．先化简，再求值：3a3﹣[a3﹣3b+（6a2﹣7a）]﹣2（a3﹣3a2﹣4a+b）其中a=2，b=﹣1，16．先化简，再求值：（5a2b+4b3﹣2ab2+3a3）﹣（2a3﹣5ab2+3b3+2a2b），其中a=﹣2，b=3．17．先化简，再求值：（a2﹣3ab﹣2b2）﹣（a2﹣2b2），其中，b=﹣8．18．先化简，再求值：8mn﹣[4m2n﹣（6mn2+mn）]﹣29mn2，其中m=﹣1，n=．19．化简求值：3（x3﹣2y2﹣xy）﹣2（x3﹣3y2+xy），其中x=3，y=1．20．先化简再求值：3x2y﹣[2xy2﹣2（xy﹣x2y）+xy]+3xy2，其中x=，y=﹣5．整式化简求值90题参考答案：1．原式=6a2﹣2ab﹣6a2+3ab=ab，当a=﹣2，b=3时，原式=ab=﹣2×3=﹣6．2．原式=6a2b+3a2b﹣5ab2﹣10a2b+6ab2=﹣a2b+ab2 ，把a=﹣2，b=代入上式得：原式=﹣（﹣2）2×+（﹣2）×2=﹣2﹣=﹣2．3．原式=3x2y2﹣5xy2+4xy2﹣3﹣2x2y2=x2y2﹣xy2﹣3当x=﹣3，y=2时，原式=454.原式=5ab2+3a2b﹣3a2b+2ab2=7ab2．当a=2，b=﹣1时，原式=7×2×（﹣1）2=14．5．原式=2x2﹣y2+2y2﹣x2﹣3x2﹣6y2=﹣2x2﹣5y2．当x=3，y=﹣2时，原式=﹣18﹣20=﹣38．6．原式=5x2﹣（x2+5x2﹣2x﹣2x2+6x）=x2﹣4x当x=时，原式=7．原式=6a2﹣6ab﹣12b2﹣6a2+12b2=﹣6ab，当a=﹣，b=﹣8时，原式=﹣6×（﹣）×（﹣8）=﹣24．8．原式=x2y﹣2xy+x2y+xy=2x2y﹣xy，当x=﹣1，y=﹣2时，原式=2×（﹣1）2×（﹣2）﹣（﹣1）×（﹣2）=﹣6．9．原式=5xy+15x2﹣10y﹣3xy﹣15x2+6y=2xy﹣4y，当x=，y=﹣1时，原式=2××（﹣1）﹣4×（﹣1）=3．10.原式=1+a+b；当a=3时，b=1，代数式的值为5；当a=﹣3时，b=﹣5，代数式的值为﹣7．a2﹣（2a2+2ab﹣b2）+（a2﹣ab﹣b2）11.原式==a2﹣2a2﹣2ab+b2+a2﹣ab﹣b2=﹣a2﹣3ab．当a=3，b=﹣2时，原式=﹣×32﹣3×3×（﹣2）=﹣3+18=1512.原式=2a2﹣ab+b2当a=﹣1，b=2．原式=2a2﹣ab+b2=2×（﹣1）2﹣（﹣1）×2+22= 813．原式=5abc﹣2a2b﹣4ab2+a2b+3abc=8abc﹣a2b﹣4ab2；a=﹣2，b=﹣1，c=3时，原式=8×2×1×3﹣4×（﹣1）﹣4×（﹣2）×1=60．14．原式=﹣2ab+6a2﹣（a2﹣5ab+5a2+6ab）=﹣2ab+6a2﹣a2+5ab﹣5a2﹣6ab=﹣3ab；当a=2，b=﹣3时，原式=﹣3×2×（﹣3）=1815．原式=3a3﹣[a3﹣3b+6a2﹣7a]﹣2a3+6a2+8a﹣2b=3a3﹣a3+3b﹣6a2+7a﹣2a3+6a2+8a﹣2b=15a+b当a=2，b=﹣1时，原式=15×2﹣1=29．16．原式=5a2b+4b3﹣2ab2+3a3﹣2a3+5ab2﹣3b3﹣2a2b=a3+3a2b+3ab2+b3，当a=﹣2，b=3时，原式=（﹣2）3+3×（﹣2）2×3+3×（﹣2）×32+33=﹣8+36﹣54+27=1．17．原式=a2﹣3ab﹣2b2﹣a2+2b2=﹣3ab，当，b=﹣8时，原式=﹣3×（）×（﹣8）=﹣12．18．原式=8mn﹣[4m2n﹣6mn2﹣mn]﹣29mn2=8mn﹣4m2n+6mn2+mn﹣29mn2=9mn﹣4m2n﹣23mn2当m=﹣1，n=时，原式=9×（﹣1）×﹣4×12×﹣23×（﹣1）×=﹣﹣2+=﹣．19．原式=3x3﹣6y2﹣3xy﹣3x3+6y2﹣2xy=﹣5xy，当x=3，y=1时，原式=﹣5×3×1=﹣15．20．原式=3x2y﹣[2xy2﹣（2xy﹣3x2y）+xy]+3xy2=3x2y﹣（2xy2﹣2xy+3x2y+xy）+3xy2=3x2y﹣2xy2+2xy﹣3x2y﹣xy+3xy2=xy+xy2，当x=，y=﹣5时，原式=×（﹣5）+×25=．。

中考分式化简求值专项练习与答案1、化简得：$\frac{x^2-2x}{2x-1}\div\frac{x+1}{x-1}$，代入$x=-2$得：$-2$2、化简得：$\frac{a^2-5a+2}{a+2}\div\frac{a^2-4}{a+4}$，代入$a=3+\sqrt{2}$得：$-3-\sqrt{2}$3、化简得：$\frac{1}{x+2}\div\frac{x^2-4}{x^2+4x-4}$，代入$x=-3$得：$-\frac{1}{2}$4、化简得：$\frac{-4}{2x(x+1)}$，代入$x=-1$得：$2$5、化简得：$\frac{2x^2-x}{(x-1)(x-2)}-\frac{x-1}{x+2}$，代入方程$x^2-x-1.5=0$的解得：$-\frac{1}{2}$6、化简得：$\frac{a-b}{a+b}+\frac{5b^2}{a^2-6ab+9b^2}$，其中$a+b=4$，代入求得整数解的不等式组得：$1$7、化简得：$\frac{1}{a-2b}-\frac{a+2b}{7a-42b}$，其中$a-b=27$，代入化简求值得：$\frac{1}{7}$8、化简得：$\frac{3x^2+4x-4}{x-2}-\frac{x-1}{x+125}$，代入方程$x^3-1=0$的解得：$-1$9、化简得：$\frac{x-1}{x-2}-\frac{1}{9}$，其中$x$是方程$x^2-x-1=0$的解，代入得：$\frac{1}{9}$10、化简得：$\frac{a^2-42}{a^2-4a+4}-\frac{a-2}{a-2}$，其中$a=-3$，代入得：$-2$11、化简得：$\frac{a-2}{2a+1}\div\frac{a+1}{a-1}\div\frac{a-1}{a+1}$，无解12、化简得：$\frac{1}{a-2}-\frac{a-2}{a+1}\div\frac{a-1}{a+1}$，其中$a=3+\frac{1}{\sqrt{2}}$，代入得：$\frac{1}{2}$13、化简得：$\frac{x-4}{x-1}-\frac{1}{x}$，其中$x=3-4$，代入得：$-2$14、化简得：$\frac{2a}{a^2-2a+1}-\frac{a}{2a+1}$，其中$x-x^2=0$的解，代入得：$0$15、化简得：$\frac{a+1}{a-2}-\frac{a^2-1}{a^2-2a+1}$，其中$a=\tan60^{\circ}$，代入得：$-1$1.代入a=12，化简得：(12)-13=-1.代入a=-13，化简得：(-13)-13=-26.2.代入x=3，化简得：3+4=7.3.化简得：1/a，代入x=3，化简得：1/(3-22)=-1/19.4.化简得：a-a^2，代入a=-7，化简得：(-7)-(-7)^2=42.。

初三30道化简求值带答案1、（3X+2Y)+(4X+3Y)其中X=5,Y=3解：原式=3X+2Y+4X+3Y=7X+5Y当X=5,Y=3时原式=5*7+（-3）*5=202、(5a²-3b²)+(a²+b²)-(5a²+3b²),其中a=-1,b=1=5a²-3b²+a²+b²-5a²-3b²=a²-5b²=(-1) ²-5*1²=1-5=-43、2 (3a- ab) -3 (2a ² - ab)，其中 a= - 2，b=3. 原式=6a ²- 2ab - 6a ²+3ab=ab，当a=-2，b=3时，原式=ab= - 2×3=-6.4、9x+6x ² -3(x-2/3x ²).其中x=-29x+6x² -3(x-2/3x²)=9x+6x²-3x+2x²=8x²+6x=8×(-2)²+6×(-2)=32-12=205、a²-ab+2b²=3 求2ab-2a²-4b²-7的值解：2ab-2a²-4b²-7=2(ab-a²-2b²)-7=-2(a²-ab+2b²)-7=(-2)*3-7=-6-7=-136、1/4(-4x²+2x-8)-(1/2x-1),其中x=1/21/4(-4x²+2x-8)-(1/2x-1)=-x²+1/2x-2-1/2x+1=-x²-1=-(1/2)²-1=-1/4-1=-5/47、2(a²b+ab²)-2(a²b-1)-2ab²-2其中a=-2,b=2=2a²b+2ab²-2a²b+2-2ab²-2=08、6a²b - ( - 3a²b+5ab²) -2 (5a²b - 3ab²)，其中a= - 2，b=1/2原式=6a²b+3a²b - 5ab² - 10a²b+6ab²= - ab+ab²把a= - 2， b=1/2代入上式得:原式= （-2）²*1/2+（-2）*1/2²=-5/29、3x²y² - [5xy² - (4xy² - 3）+2x²y²]，其中x=- 3，y=2原式=3x²y² - 5xy²+4xy² - 3- 2x²y²=x²y²- xy²- 3当x=- 3，y=2时，原式=4510、2x-3(2x-x)+(2y-y),其中x=1,y=2解；原式=2x-3x+y当x=1,y=2时原式=2*1-3*1+2=2-3+2=111、5ab²+3a²b - 3 (a²b - ab²)，其中a=2，b= - 1原式=5ab²+3a²b - 3a²b+2ab²=7ab²当a=2，b=- 1时，原式=7×2×( -1)2=1412、2a-（3a-2b+2）+（3a-4b-1),其中a=5 b=-3=2a-3a+2b-2+3a-4b-1=（2-3+3）a+（2-4）b+（-2-1）=2a-2b-3=10-(-6)-3=10+6-3=1313、5-(1-x)-1-(x-1）-2x+(-5y）,其中x=2,y=2x=4-2x-5y=4-4-20=-2014、2x-(x+3y)-(-x-y)-(x-y),其中x=3,y=-3=2x-x+3y+x+y-x+y=x+5y=3-15=-1215、-ab+3ba-(-2ab),其中a=2,b=1=-ab+3ba+2ab=2ab+2ab=4ab=4*2*1=816、-m-[-(2m-3n)]+[-(-3m)-4n],其中m=2,n=1 =-m-(-2m+3n)+3m-4n=-m-4m+2m-3n+3m=-3n=-3*1=-317、2（2a+2ab)-2(2ab-1)-2ab-2,其中a=-2 b=2 =4a+4ab-4ab+2-2ab-2=4a-2ab=4*(-2)-2*(-2)*2=-8-(-8)=-8+8=018、3ab-4ab+8ab-7ab+ab,其中a=-2,b=3=-8ab+9ab=ab=-2*3=-619、2x²- y²+ (2y² - x²) - 3 (x²+2y²)，其中 x=3，y= - 2原式=2x² - y²+2y² - x² - 3x² - 6y²= - 2x²- 5y²当x=3，y=-2时，原式=– 18- 20= - 3820、5x²- [x² +(5x²- 2x） - 2 (X²- 3x)]，其中x=1.原式=5x² - (x²+5x²- 2x - 2x²+6x） =x ² - 4x当x=1/2时，原式=7/421、( 6a²- 6ab - 12b²) - 3 (2a²- 4b²)，其中 a=-1/2， b=- 8. 原式=6a² - 6ab - 12b² - 6a²+12b3²= - 6ab，当a=-1/2， b=-8时，原式=-6x( -1/2) ×( -8） =- 24 22、x²y - (2xy - x²y)+xy，其中x=- 1，y= - 2.原式=x²y - 2xy+x²y+xy=2x²y - xy，当x= - 1，y=-2时，原式=2*( - 1) ²* ( -2） - ( -1) *( - 2） = - 623、当|a|=3，b=a -2时，化简代数式1- {a - b - [a - (b - a)+b]}后，再求这个代数式的值.原式=1+a+b;当a=3时，b=1，代数式的值为5;当a=-3时，b=- 5，代数式的值为–724、- 2(ab - 3a²) - [a²- 5 (ab - a²) +6ab]，其中 a=2，b=- 3原式= -2ab+6a² - (a² - 5ab+5a² +6ab） = - 2ab+6a² - a² +5ab - 5a² - 6ab= - 3ab;当a=2，b=-3时，原式=–3×2×( -3） =1825、( a² - 3ab - 2b²) - (a² - 2b²)，其中a= - 1/2. b= - 8原式=a²- 3ab - 2b² - a²+2b²= - 3ab，当a=-1/2 ，b=-8时，原式= -3×( -1/2) ×( -8）= - 1226、8mn - [4m²n - ( 6mn² +mn) ] - 29mn²，其中 m= - 1，n=1/2原式=8mn - [4m²n - 6mn²- mn] - 29mn²=8mn - 4m²n+6mn²+mn - 29mn²=9mn - 4m²n - 23mn²当m=- l，n=1/2时，原式=9× ( - 1)×1/2-4×1²×1/2- 23x ( - 1)×1/4=-9/2-2+23/4=-3/427、（3X+2Y)+(4X+3Y)其中X=5,Y+3原式=3X+2Y+4X+3Y=7X+5Y当X=5,Y=3时原式=5*7+（-3）*5+20=35-15+20=4028、2x-3(2x-x)+(2y-y),其中x=1,y=2解；原式=2x-3x+y当x=1,y=2时原式=2*1-3*1+2=2-3+2=129、2a-（3a-2b+2）+（3a-4b-1),其中a=5 b=-3 =2a-3a+2b-2+3a-4b-1=（2-3+3）a+（2-4）b+（-2-1）=2a-2b-3=10-(-6)-3=10+6-3=1330、2x-(x+3y)-(-x-y)-(x-y),其中x=3,y=-3=2x-x+3y+x+y-x+y=x+5y=3-15=-12。