小学二年级数学下册 长方体、正方体应用题名师精编练习 西师大版
- 格式:doc
- 大小:32.00 KB
- 文档页数:2
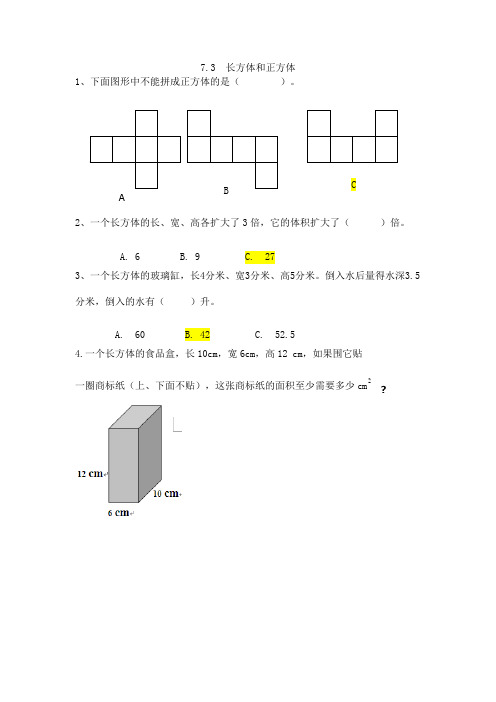
7.3 长方体和正方体1、下面图形中不能拼成正方体的是( )。
2、一个长方体的长、宽、高各扩大了3倍,它的体积扩大了( )倍。
A. 6B. 9C. 27 3、一个长方体的玻璃缸,长4分米、宽3分米、高5分米。
倒入水后量得水深3.5分米,倒入的水有( )升。
A. 60B. 42C. 52.54.一个长方体的食品盒,长10cm ,宽6cm ,高12 cm ,如果围它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少需要多少cm 2A B C?答案1.C2.C3.B4.384(赠品,不喜欢可以删除)数学这个家伙即是科学界的“段子手”,又是“心灵导师”一枚。
它要是给你讲起道理来,那可满满的都是人生啊。
1.人生的痛苦在于追求错误的东西。
所谓追求错误的东西,就是你在无限趋近于它的时候,便无限远离了原点,却永远无法和它产生交点。
2.人和人就像数轴上的有理数点,彼此可以靠得很近很近,但你们之间始终存在无理的隔阂。
3.人是不孤独的,正如数轴上有无限多个有理点,在你的任意一个小邻域内都可以找到你的伙伴。
但人又是寂寞的,正如把整个数轴的无理点标记上以后,就一个人都见不到了。
4.零点存在定理告诉我们,哪怕你和他站在对立面,只要你们的心还是连续的,你们就能找到你们的平衡点。
5.有限覆盖定理告诉我们,一件事情如果是可以实现的,那么你只要投入有限的时间和精力就一定可以实现。
至于那些在你能力范围之外的事情,就随他去吧。
6.幸福是可积的,有限的间断点并不影响它的积累。
所以,乐观地面对人生吧!。

西师大版五年级下册数学第三单元长方体正方体应用题训练1.一间教室,从里面量长为12米,宽为8米,高为45米。
教室门窗、和黑板的面积一共有28平方米。
要粉刷教室的顶部和四面墙壁,粉刷的面积有多少平方米?2.有一个长方体木块正好可以切成两个完全相同的小正方体木块,已知长方体木块的棱长总和是80分米,这个长方体木块的表面积是多少平方分米?3.妈妈给丽丽买了一个长方体形状的蚊帐(如图),蚊帐的四周由钢管固定(地面的四边没有钢管)。
固定这样一个蚊帐,至少需要多长的管?4.一根铁丝可以围成如图所示的长方体框架,如果用它围成一个正方体框架,那么这个正方体框架的棱长是多少厘米?5.拨浪鼓在古代是一种乐器,多用于历代宫廷雅乐。
明明根据它的特点用体积是135cm3的长方体塑料盒自制了一个拨浪鼓。
塑料盒长6cm,宽2.5cm,它的高是多少厘米?6.用一根88 cm 长的铁丝围成一个长方体框架,再在外面糊一层纸。
已知它的长是高的3倍,宽比长短6 cm。
长方体的体积是多少立方厘米?7.小老鼠杰瑞做了一些奶酪,汤姆想:“一定很好吃,我要吃大的。
”汤姆选择哪一种才能吃到更多的奶酪呢?(尺寸如图,单位:cm)8.一个长方体木块,如果它的高减少3 dm,就成为一个正方体这时它的表面积减少72 dm2。
原来这个长方体的表面积是多少平方分米?9.如图,在一个长20 dm、宽8 dm、高10 dm的长方体水槽中注入6 dm 深的水,然后放入一个棱长为 4 dm 的正方体铅块(铅块完全浸没在水中),则水位上升了多少分米?10.如图,某广场上有16根这样的石墩,在每根石墩四周的表面贴上瓷砖。
若瓷砖每平方米120元,则给这些石墩贴瓷砖一共要花多少元?(单位:cm)11.把10L水倒入一个底面是边长为2.5dm的正方形、高5dm的长方体水缸里。
(1)这时水面的高度离容器口有多少分米?(2)此时,将一个正方体铁块全部浸没在水中,水面上升了1.5dm。

青岛版小学数学《长方体和正方体的整理复习》课堂实录一、创设情境,导入单元复习师:同学们好!今天我们第一次见面,老师给同学们带来两件小礼物,你们能根据它们的形状大小猜一猜是什么吗?(包装好的一盒牛奶和一个魔方)生1:里面是一个长方体生2:里面装的是一个长方体盒子,盛的是液体师:这位同学猜的比较准确,(举魔方)这是什么?生1:是一个正方体生2:是一个魔方师:这位同学的眼力真不错,猜不出来的同学也没关系,生活中像这样形状的物品实在太多了。
老师给你们带来的是一盒牛奶和一个魔方,这两件礼物包含了两层含义:一层含义是老师对同学们的祝福,希望同学们身体倍棒,健康成长(手举奶盒),头脑灵活,越来越聪明(举魔方);另一层含义,这两件东西是我们这节课学习的小助手,你知道这节课我们要学习什么了吗?板书:长方体和正方体的整理复习二、全班交流本单元内容师:请同学们回忆我们都学过长方体和正方体的哪些知识?生答,板书:特征、表面积、体积和体积单位、容积和容积单位、体积的计算师:这么多的知识有没有什么好办法让他们系统条理的展现出来呢?三、单元知识整理,形成知识体系学生小组为单位结合课本和单元目标导学整理本单元内容,看哪个组整理的快,汇报的好。
学生小组讨论整理,小组长做好记录,整理出本单元的知识体系。
四、全班汇报交流师:每个小组汇报时,可选择一个知识点来说,让每个小组都有发言的机会。
生1:我们小组想汇报长方体和正方体的特征,长方体和正方体都有12条棱,8个顶点,6个面。
生2:长方体相对的两个面完全相同,相对的棱长度相等,可以根据长度不同把长方体的棱分成3组,每组4条。
生3:正方体的6个面完全相同,而且都是正方形,12条棱都相等。
师:他们对长方体和正方体的知识掌握的真熟练,还有补充的吗?生:长方体的特殊情况有两个面是正方形时,其余的四个面都完全相同。
评价:补充的非常好,知识更全面了。
师:学习了一部分知识后,我们要善于总结和比较知识之间的联系和区别,这样更有利于我们对知识的掌握。

小学五年级数学(下)《长方体、正方体体积的计算》练习题一、填一填。
1、一段方钢长4分米,横截面是25平方厘米的正方形,这方钢的体积是()。
2、挖一个长和宽都是5米的长方形菜窖,要使菜窖的容积是50立方米,应挖()米深。
3、一个长方体纸箱,长5分米,宽3分米,高4分米,它的所有棱长的和是()分米。
体积是()立方分米。
4、一个正方体的棱长是5厘米,它的表面积是()平方厘米,体积是()立方分米。
5、一个长25厘米,宽12厘米,厚8厘米的砖,所占空间是()立方厘米,占地面积是最大是()平方厘米。
6、在()里填上合适的数。
3.05m3=()dm37200cm3=()dm34.6L=()dm39.8m3=()L 8L=()cm3520mL=()cm32m3=()dm30.35dm3=()cm3 4.15dm2=()cm272.5dm2=()cm2950mL=()cm310020dm3=()m37、一台洗衣机体积约300(),汽车油箱的大约能装汽车50()二、判断。
1、棱长6厘米的正方体,表面积和体积相等。
()2、把一块正方体橡皮泥捏成一个长方体后,虽然形状变了,但它所占的空间大小不变。
()3、正方体和长方体的体积都可以用底面积×高来计算。
()4、长方体的底面积越小,它的体积就越小。
()5、体积单位比面积单位大。
()6、一个长方体的底面是边长4厘米的正方形,高是5厘米,它的体积是20立方厘米。
()三、选择。
1、将一个正方体钢坏锻造成长方体,正方体和长方体().A、体积相等,表面积不相等B、体积和表面积都不相等C、表面积相等,体积不相等。
2、把正方体的棱长扩大2倍,则体积扩大()倍。
A、2B、6C、83、一个长方体的长、宽、高都扩大2倍,它的体积扩大()倍。
A、2B、6C、84、一个长方体的底面积是15平方厘米,高是5厘米,它的体积是()A、75厘米B、75平方厘米C、75立方厘米5、把一个棱长4厘米的正方体锯成棱长1厘米的小正方体,可锯()个。

《长方形与正方形》说课稿一、教材分析1、教材的地位及作用《长方形与正方形》是小学数学北师大版第4册第七单元“认识图形”的第2课时,属于《空间与图形》范畴,之前学生对长方形和正方形已经有了初步认识,能够正确区分锐角、直角、钝角,本节课在此基础上,学生通过动脑、动手、动口等一系列学习活动进一步加深对长方形和正方形特征的认识,了解长方形与正方形之间的联系。
同时这节课的教学也为学生今后学习长方形和正方形的周长与面积以及认识长方体和正方体的特征奠定良好的基础,所以在教材中有着承上启下的作用。
2、目标分析:根据上述教材分析及儿童的心理特点,我把本节课的学习目标定为:(1)通过操作、比较、归纳,能够用自己的语言描述长方形、正方形的特征。
(2)通过一系列操作活动,让学生体验长方形和正方形特征的认识过程,积累认识图形的方法,获得研究图形的有关经验。
(3)通过创设活动情境,激发学生的学习兴趣,培养学生的探究精神及合作意识。
3、教学重难点。
教学重点:掌握长方形和正方形特征。
教学难点:长方形和正方形特征的联系与区别。
二、教法与学法分析为了更好地达到教学三维目标,突破本节课的重难点,我准备采用观察发现法、活动探究、小组活动等教学法。
所以本节课将以活动贯穿始终,让学生在活动中动脑思考、动手操作、自主探究、合作交流。
三、教学过程分析基于我确定的学习目标及教学重难点,我的教学过程将从以下四个步骤展开:(一)设情引趣、导入新课。
新课标指出应让学生在积极生动的情境中学习数学,良好的开端是课堂教学成功的一半,基于这个认识,我设计了这样一个竞赛活动情境,每个小组有长短不一的三种小棒,每次任意拿出其中的4根摆出不同的四边形,在相同的时间内看哪组摆得多,摆得好!一分钟后,学生摆出的各种不同的四边形一一展示在黑板上。
指着这些不同的四边形我问道:“这些四边形中,你最熟悉的是谁呢?”学生可能会说:“长方形、正方形”我故意问道:“老师有个问题不明白,这也是四边形,这也是四边形,为什么它叫长方形,它叫正方形呢?”。

3.1 长方体、正方体的认识◆教学内容教材第38-41页“长方体和正方体的特征”,课堂活动及练习十二的相关内容。
◆教材提示本节课是在学生具有了以实物来认知长方体和正方体的基础上,进一步学生和掌握长方体和正方体的特征。
通过本节课的学习,要让学生掌握:第一:长方体和正方体各部分的名称。
第二:长方体和正方体的特征。
第三:长方体和正方体之间的关系。
第四:求长方体和正方体棱长和的方法。
在教学中要注意,可以从以下几个方面进行展开教学。
1.在情境中展开教学,发动学生的多种感官来学习。
首先通过摸一摸,让学生运用感觉思维来认识面,棱和顶点的特征。
再通过数一数来总结和掌握长方体和正方体的特征,认识长方体的长、宽、高。
最后可以通过量一量和比一比。
认识长方体对面相等,正方体6个面都相等;长方体棱分3组,每一组4条棱都相等,正方体12条棱都相等的特征。
2.通过三视图的训练,主要是培养学生的空间的观念和意识。
3.在教学中,要充分发挥小组合作的学习优势,让学生在摸,量,比,测的基础上,通过小组内成员的讨论交流中,发现共同的规律,从而顺利地总结长方体和正方体的形体特征。
◆教学目标知识与技能:通过观察、操作,认识并掌握长方体和正方体的特征。
认识长方体的长、宽、高。
通过三视图的观察和理解,培养学生的空间思维能力。
过程与方法:让学生在操作过程中经历探究的全过程,通过合作学习,进一步积累探索经验,增强学生的空间观念,发展学生的数学思维。
情感、态度和价值观:让学生体会立体图形学习与实际生活的联系,感受其价值,增强数学学习的兴趣和学好数学的自信心。
◆重点、难点重点长方体和正方体的特征。
掌握长方体和正方体的面、棱的特征。
难点培养学生的对立体图形的空间观念。
◆教学准备教师准备:课件,长方体、正方体若干。
学生准备:长方体、正方体纸盒或物品。
◆教学过程(一)新课导入:1.分一分。
课件出示各种长方体,正方体、三棱体,圆锥体等。
让学生分一分,看一看,哪些是长方体,哪些是正方体?哪些既不是长方体也不是正方体?并说一说为什么?2.想一想。
长方体、正方体的认识
1.【综合应用题】一根长方体木料,长是2 dm,宽是4 dm,高是6 dm。
最多可以锯成多少个棱长是2 dm的正方体?
2.【生活情境题】“母亲节”这天,佳佳为妈妈准备了一份礼物,并要在长12 cm,宽8 cm,高4 cm的盒子上扎一条彩带,彩带接头处长10 cm,一共需要多少厘米彩带?
3.【生活情境题】爸爸给欣欣买了一台点读机,包装盒是长为40 cm,宽为30 cm,高为6 cm 的长方体。
(1)它最大的面的面积是多少平方厘米?合多少平方米?
(2)你还能提出什么数学问题?
4.【探究题】用8个棱长是2 cm的正方体拼成一个大正方体,棱长和是多少厘米?
答案
1.(6÷2)×(2÷2)×(4÷2)=6(个)
2.8×2+12×2+4×4+10=66(cm)
3.(1)40×30=1200(cm2) 1200 cm2=0.12 cm2
(2)(答案不唯一)最小的面积是多少?30×6=180(cm2)4.(2+2)×12=48(cm)。
数学西师大版五年级下册《长方体和正方体的体积运算》基础练习题号一二三四得分注意事项:1.本试卷共XX页,四个大题,满分85分,考试时间为1分钟。
请用钢笔或圆珠笔直接答在试卷上。
2.答卷前将密封线内的项目填写清楚。
一、单选题(共15分)评卷人得分1.正方体的棱长扩大了2倍,则体积扩大( )倍。
(5分)A. 2B. 4C. 82.表面积相等的长方体和正方体的体积相比,( )。
(5分)A. 正方体体积大B. 长方体体积大C. 相等3.一个长方体的长、宽、高分别是8 m,5 m,9 m。
如果高增加2 m,体积比原来增加( )cm3。
(5分)A. 90B. 80C. 144二、判断题(共25分)评卷人得分4.一个正方体的棱长总和是12 cm,体积是1 cm3。
( )(5分)5.棱长为6 cm的正方体的体积和表面积相等。
( )(5分)6.表面积相等的两个正方体,它们的体积一定相等。
( )(5分)7.用一根12 dm长的铁丝围成一个最大的正方体框架,这个正方体的体积是12 cm3。
( )(5分)8.一个长方体的高不变,底面积扩大3倍,它的体积就扩大3倍。
( )(5分)三、填空题(共35分)评卷人得分9.一个长方体的底面积是0.3 m2,高是0.1 m,它的体积是( )立方分米。
(5分)10.一个长方体的体积是30 cm3,长是5 cm,高是3 cm,宽是( )cm。
(5分)11.一个正方体的棱长总和是36 cm,这个正方体的表面积是( ),体积是( )。
(5分)12.一个表面积是54 cm2的正方体,它的体积是( )cm3。
(5分)13.把三个棱长是2 cm的正方体拼成一个长方体,表面积是( ),体积是( )。
(5分)14.一个棱长是5 dm的正方体鱼缸,蓄水后水面低于缸口1 dm,水的体积是( )dm3。
(5分)15.一根长方体木料,它的横截面的面积是0.15 m2,长是4 m。
7根这样的木料体积一共是( )m3。
3.1长方体、正方体的认识1.以下图中能表示长方体和正方体关系的是〔〕。
2.一个长方体〔不包括正方体〕,最多有〔〕个面的正方形。
A.1B.2C.33.以下图形中,〔〕是正方体。
4.用一根长72m的铁丝,焊接一个长10m,宽6m的长方体,这个长方体的高为多少米?答案1.C2.B3.C4.2立体图形〔2〕1.一辆货车车厢是长方体,它的长是4m,宽是2.5m,高是1.5m(从里面量),装满一车沙,卸车后沙堆形成一个高是5m的圆锥形。
它的底面积是多少?2.做50节底面直径为20cm,长3m的烟筒,至少需要多少平方米的铁皮?3.一台压路机,滚筒直径是1m,宽1.2m,压路时每分钟滚动15周,这台压路机每分钟前进了多少米?每分钟可以压路多少平方米?4.洪山广场有一个圆柱形音乐喷水池,底面直径8m,深0.8m。
(1)如果要在水池的底面和内壁贴上瓷砖,贴瓷砖的面积是多少平方米?(2)每平方米瓷砖35元,购置瓷砖需要多少元?(3)每立方米水重1吨,这个水池最多能装多少吨水?4.下面这个容器一共能装多少毫升水?(容器壁的厚5.一台洗衣机长0.6m,宽0.5m,高0.8m。
(1)做这台洗衣机的包装箱至少需要多少平方米纸板?〔2〕这台洗衣机占地面积是多少平方米?6.三峡泄洪坝共有23个长方形的泄洪孔,每个泄洪孔的宽是21米,高是126米。
(1)23个泄洪孔的横截面积一共是多少平方米?(2)泄洪时,通过泄洪孔的水流速度是每秒1.8米。
23个泄洪孔每时的水流量是多少立方米?7. 有甲、乙两个容器(如以下图),先将甲容器注满水,然后将水倒入乙容器,那么水深多少厘米?8.小明感冒了,妈妈送他到医院输液,一瓶液100mL ,每分钟输2.5mL 。
小明观察到输到12分钟时,吊瓶中数据如图,整个吊瓶的容积是多少?答案1.4×2.5×1.5÷(3×5)=9(m2)2.20cm=0.2m3.14×0.2×3×50=94.2(m2)3×1×15=47.1(m)47.1×1.2=56.52(m2)4.8dm=80cm10m=100cm15dm=150cm150×150×150+3.14×(80÷2)2×100=3877400(cm3)=3877400(mL)5.(1)(0.6×0.5+0.6×0.8+0.8×0.5)×2=2.36(m2)(2)0.6×0.5=0.3(m2)6.(1)126×21×23=60858(m2)(2)60858×1.8×3600=394359840(m3)7.31×3.14×62×10=376.8(cm3)376.8÷(3.14×42)=7.5(cm) 8.100-2.5×12+80=150(mL)。
(一)一、直接写出得数2.4+5.9= 6÷0.2= 8.4×2= 5.1-2.9= 1.4×0.7=3.7-2.4= 8.4÷0.7= 30×1.2= 0.15×0.3= 7.2÷0.12=二、数学小法官(正确的打“√”,错误的打“×”)1.把一个表面积是54平方厘米的正方体木块,平均分成两个长方体,每个长方体的表面积是36平方厘米。
()2.长方体上没有正方形的面。
()3.长方体相邻的两个面的面积不一定不相等。
()4.正方体棱长扩大3倍,它的表面积扩大6倍。
()5.两个正方体的表面积都是24平方厘米,用这两个正方体拼成长方体后长方体的表面积是48平方厘米。
()三、生活中的问题一间教室长10米,宽6米,高4米,现要粉刷屋顶和四壁,除去门窗面积20平方米,如果每平方米需工料费1.5元,粉刷这间教室共需工料费多少元。
(二)一、我会填1.长方体或者正方体的__________的总面积,叫做它的表面积。
2.一个长方体,其中有三个面的面积分别是9平方厘米、8平方厘米、6平方厘米,这个长方体的表面积是__________平方厘米。
3.一个长方体长是10分米,宽是8.5分米,高是4分米,它的表面积是__________平方分米,棱长之和是__________。
4.一个棱长4米的正方体盒子,它的表面积是__________平方米,如果把它的上盖去掉,这个正方体盒子的表面积是__________平方米。
二、对号入座1.一个长方体的纸盒长15厘米,宽12厘米,高10厘米。
(1)它的底面积是()。
A.180平方厘米B.150平方厘米C.120平方厘米(2)它的4个侧面的面积之和是()。
A.720平方厘米B.540平方厘米C.300平方厘米(3)它的6个面的总面积是()。
A.600平方米B.800平方厘米C.900平方厘米2.一个正方体的棱长之和是24厘米,它的表面积是()平方厘米。
长方体和正方体应用题练习
1、两根同样长的铁丝焊一个长方体和正方体,长方体长7厘米,宽5厘米,高3厘米,正方
体的棱长是多少厘米?
2、一个长方体水池,长2米,宽1.2米,深0.8米,现将水池的四壁和底部抹上一层水泥,
求抹水泥的部分的面积是多少平方米?
3、水泥厂制10根长方体铁皮通风管道管子,横截面为边长30厘米的正方形,管全长2米,
共需多少平方米铁皮?
4、用两个棱长是1分米的正方体木块拼成一个长方体时,拼成的长方体表面积与原来相比,
减少了多少?
5、要做一个正方形管口周长是28厘米,长2米的通气管子10根,至少需要铁皮多少平方米?
6、一个长方体玻璃容器,底面积是250平方厘米,高12厘米,里面盛有6厘米的水,现将
一块石头放入水中,水面上升了4厘米,这块石头的体积是多少立方厘米?
7、给一个棱长是1.2米的正方体铁箱油漆一遍,(内外两面)油漆部分面积是多少平方米?
8、把一根长3米的长方体木料据成3段后,表面积增加18平方分米,这根木料原来的体积
是多少立方米?
9、一根长1.8米,横截面是边长5厘米的正方形的长方体铜条,铜条如果每立方分米重8.9
千克,这根铜条共重多少千克?
10、长方体,如果长减少3厘米,就是一个正方体,这个正方体的表面积是96平方厘米,原来长方体的体积是多少立方厘米?
11、一个长方体容器,底面长60厘米,宽38厘米,里面沉入一个长方体钢块,当钢块取出时,容器中的水面下降5厘米,如果长方体钢块的底面积是570平方厘米,钢块高多少厘米?
12、有一个装饼干的正方形铁盒,底面是正方形,边长是20厘米,高是30厘米,这个铁盒四周印满商标,商标的面积是多少平方厘米?
13、一个长方体和一个正方体的表面积一共有525平方厘米,长方体的表面积是正方体的2.5倍,长方体和正方体的表面积各是多少平方厘米?(用方程解)
14、一个教室长8米,宽5米,高4米。
要粉刷教室的顶面和四周墙壁,除去门窗面积21.5平方米,粉刷面积是多少平方米?如果每平方米用油漆0.25千克,共要用油漆多少千克?15、一个长方体蓄水池,长12米,宽8米,高4米,如果将四壁和地面用4平方分米的正方形瓷砖贴上,需要多少块?
16、把一块棱长1.2米的正方体钢坯锻成横截面面积是0.04平方米的长方体钢材,锻成的钢材有多长?
17、一个长方体的长是15厘米,宽是12厘米,棱长总和是148厘米,它的高是多少?
18、一个长方体油箱,底面是一个正方形,边长是6分米,里面已盛油144升,已知里面油的深度是油箱深度的一半,这个油箱深多少分米?
19、把一根5米长的长方体木料据成5段后,表面积比原来增加128平方厘米。
这根木料的体积是多少立方厘米?
20、一个水池长6米、宽5米、高1.5米,池里所储的水是36立方米,问现在水面距池口多少米?
21、一个长60厘米、宽20厘米的盛水容器,把5块体积相等的铁块投入水中,容器中的水面正好上升了4厘米,求每块铁块的体积。
22、一张办公桌有3个抽屉,每个抽屉长50厘米、宽30厘米、高10厘米。
做这张办公桌的抽屉至少需要木板多少平方厘米?
23、把一根长2.4米,宽0.8米,高0.4米的木料据成体积相等的2份,它的表面积最少增加多少平方米?
24、一个现代化的体育馆里,铺设了20块长30米、宽3.5米、厚0.3米的木质地板,这个体育馆占地面积是多少?地板的体积一共是多少?
25、把110厘米长的铁丝焊成一个长方体框架,长是宽的2倍,宽是高的1.5倍,这个长方体的体积是多少?
26、有一个长方体浴室,长4.6米,宽2.5米,高2米。
这个浴室的占地面积是多少平方米?如果将四壁和底面用瓷砖贴上,至少需要多少平方米的瓷砖?xk b 1.co m
27、一种长方体的通风管,长是4米,宽和高都是16厘米,做一根这样的通风管至少需要多少平方米的铁皮?
28、把一个长70厘米、宽50厘米、高50厘米的长方体木块削成一个体积最大的正方体,削去部分的体积是多少立方分米?
29、一个正方体棱长的总和是96分米,它的表面积和体积各是多少?
30、一个长方体的长、宽、高分别是11厘米、6厘米、4厘米,如果高增加3厘米,表面积增加多少平方厘米?
31、一个正方体木块,表面积是30平方分米,如果把它据成大小一样的8个小正方体木块,每个小木块的表面积是多少?
32、一块长方体石料,长4分米,横截面是一个边长为0.5分米的正方形,这块石料的表面积是多少?如果每立方分米石料重2.7千克,这块石料有多重?
33、一个长方体,底面周长为3.6分米的正方形,高是3分米。
它的体积是多少?。