最新8第八章复合控制系统汇总

第八章 非线性控制系统分析8-1 非线性控制系统概述1. 研究非线性控制理论的意义以上各章详细地讨论了线性定常控制系统的分析和设计问题。

但实际上，理想的线性系统并不存在，因为组成控制系统的各元件的动态和静态特性都存在着不同程度的非线性。

以随动系统为例，放大元件由于受电源电压或输出功率的限制，在输入电压超过放大器的线性工作范围时，输出呈饱和现象，如图8-l(a)所示；执行元件电动机，由于轴上存在着摩擦力矩和负载力矩，只有在电枢电压达到一定数值后，电机才会转动，存在着死区，而当电枢电压超过一定数值时，电机的转速将不再增加，出现饱和现象，其特性如图8-1(b)所示；又如传动机构，受加工和装配精度的限制，换向时存在着间隙特性，如图8-1(c)所示。

在图8-2所示的柱形液位系统中，设H 为液位高度，Q i为液体流入量，Q o 为液体流出量，C 为贮槽的截面积。

根据水力学原理0Q k H = (8-1)其中比例系数k 是取决于液体的粘度和阀阻。

液位系统的动态方程为0i i dH CQ Q Q k H dt =-=-显然，液位H 和液体输入量Q i 的数学关系式为非线性微分方程。

由此可见，实际系统中普遍存在非线性因素。

当系统中含有一个或多个具有非线性特性的元件时，该系统称为非线性系统。

一般地，非线性系统的数学模型可以表示为：(,,...,,)(,,...,,)n m n m d y dy d r dr f t y g t r dt dt dt dt =(8-3)其中f(·)和g(·)为非线性函数。

当非线性程度不严重时，例如不灵敏区较小、输入信号幅值较小、传动机构间隙不大时，可以忽略非线性特性的影响，从而可将非线性环节视为线性环节；当系统方程解析且工作在某一数值附近的较小范围内时，可运用小偏差法将非线性模型线性化。

例如，设图8—2液位系统的液位H 在H 0附近变化，相应的液体输入量Q i 在Q i0，附近变化时，可取ΔH =H −H 0，ΔQ i =Q i −Q i0,对√H 作泰勒级数展开。

能否想一个办法使得，既能消除系统的稳定误差，又能保证系统稳定性不变的目的。

——于是引入了复合控制。

为此人们提出了一种即提高了系统的稳态精度，又不影响系统的稳定性的措施——复合控制系统。

1． 什么叫复合控制系统：复合控制系统是系统的反馈控制回路中加入前馈通路，组成一个前馈控制与反馈相结合的的系统，只要系统参数选择合适，不但可以保持系统稳定，极大地减小乃是消除稳态误差，而且可以抑制几乎所有的可量测扰动。

这是将第六章的内容提前。

复合控制系统是在反馈控制系统中加入前馈（顺馈） 控制。

复合控制系统的基本构成是反馈控制系统，前馈控制是用来补偿反馈系统的不足之处。

顺馈是相对于反馈而言的，相当于开环控制。

由前面的讨论可知，提高系统的开环增益和增加系统的类型是减小和消除系统稳态误差的有效方法。

但这两种方法在其他条件不变时，一般都会影响系统的动态性能，乃至系统的稳定性。

若在系统中加入顺馈控制作用，就能实现既减小系统的稳定误差，又能保证系统稳定性不变的目的。

（1） 按扰动补偿的复合控制——已知扰动或可直接测量。

如果系统的误差主要由某一处加干扰信号引起的，并且该干扰或是可直接测量的，或是可间接测量的，总之是可测的，那么能不能用不变性原理来消除干扰信号的影响呢？也就是说 ()0n E s =或者()()0()en E s s N s Φ==。

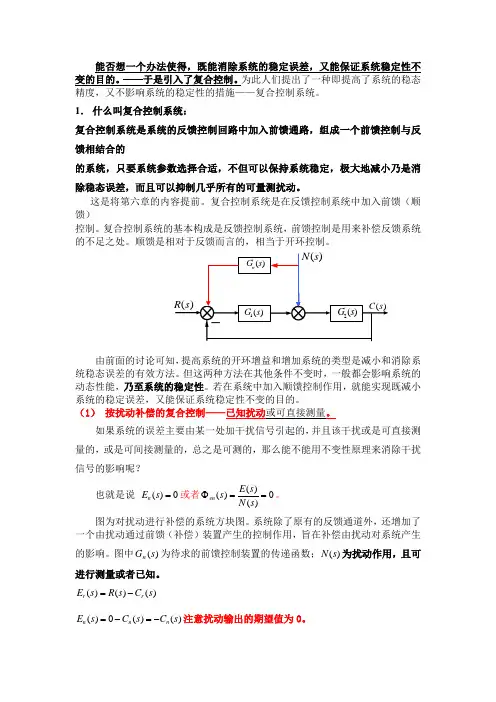
图为对扰动进行补偿的系统方块图。

系统除了原有的反馈通道外，还增加了一个由扰动通过前馈（补偿）装置产生的控制作用，旨在补偿由扰动对系统产生的影响。

图中)(s G n 为待求的前馈控制装置的传递函数；)(s N 为扰动作用，且可进行测量或者已知。

()()()r r E s R s C s =-()0()()n n n E s C s C s =-=-注意扰动输出的期望值为0。

因此，12()0()()[()()]n n n n n E s C s C s C s C s =-=-=-+其中，1()n C s 为没有加顺馈时的实际输出， 2()n C s 为顺馈补偿得出的实际输出2112()()()1()()n G s C s N s G s G s =+12212()()()()()1()()n n G s G s G s C s N s G s G s =+两个信号叠加。