当前位置：文档之家 › 气体动力学函数及应用

气体动力学函数及应用

  • 格式：ppt
  • 大小：862.00 KB
  • 文档页数：49

下载文档原格式

  / 49

合集下载

空气动力学第三章

空气动力学第三章

⎡ ⎤ ⎥ ρ ⎢ γ +1 = ⎢ ⎥ ρ * ⎢ 2(1 + γ − 1 M 2 ) ⎥ 2 ⎣ ⎦
（3.13）
γ /( γ −1)
（3.14）
⎡ ⎤ ⎥ γ +1 c ⎢ = ⎢ ⎥ c* ⎢ 2(1 + γ − 1 M 2 ) ⎥ ⎣ ⎦ 2
1/2
（3.15）
考虑能量方程：
V = 2c p (T0 − T ) = 2γ R (T0 − T ) γ −1
& m G * = ( ) max A
R (1 + γ − 1 M 2 )(γ +1)/[2(γ −1)] 2 & p γ 2 (γ +1)/(γ −1) m = *= 0 ( ) A T0 R r + 1
γ
M
A G 1 2 γ − 1 2 ( γ +1)/[ 2( γ −1)] M )] = = [( )(1 + * A G M γ +1 2
γ − 1 *2 M γ +1
马赫数和临界马赫数的关系曲线如图3.6所示：
当M<1时,M*<1; 当M=1时,M*=1; 当M>1时,M*>1; 当M趋近无穷时;
M* = r +1 r −1
• 3.4 由马赫数表示的质量流流率
& m G = = ρV A
ρ = p / RT
c = γ RT
V γ G = p( ) c RT
V2 = M2 γ RT
T0 γ −1 2 = 1+ M T 2
（3.4 ）
cp =
γR γ −1
公式（3.4）实用于绝热流动和等熵流动。
对于完全气体的等熵流动，其压力和密度与温度的关系 为： p0 T0 γ /(γ −1) ρ0 T0 1/(γ −1) =( ) =( ) T ρ p T 将上述公式与（3.4）结合起来，可以得到压力和密度由 马赫数来表示的关系式如下：
气体动力学基础PPT课件

气体动力学基础PPT课件


气体动力学基础_1
23
第二章 一维定常流的基本方程
§2.1 应知的流体力学基本概念
• 无限多个连续分布的流体微团 组成的连续介质的假设（
Euler明确，1752）。而非分子论。适用于l/L<1/100，例
如100公里以下的大气与飞行器
• 一维定常流 1-D Steady flow，流线 Streamline，
3
第一章 绪论
§1.1 气体动力学的涵义
气体动力学是
➢ 流体力学的一个分支，在连续介质假设下，研
究与热力学现象有关的气体的运动规律及其与
相对运动物体之间的相互作用。
➢ 气体在低速流动时属不可压缩流动，其热力状
态的变化可以不考虑；但在高速流动时，气体
的压缩效应不能忽略，其热力状态也发生明显
的变化，气体运动既要满足流体力学的定律，
学科名 Discipline 流体力学 Fluid Dynamics 空气动力学 Aerodynamics 气体动力学 Gas Dynamics
主要研究范围 Primary Scope
不可压缩流体动力学 Incompressible Fluid Flow
不可压缩＋可压缩流体动力学 Incom-＋Com-pressibleLeabharlann 解析解，螺旋桨理论，飞机设计
1904-20年代，普朗特Prandtl（德）的普朗特－迈耶流动理论，（超音
速膨胀波和弱压缩波），风洞技术，边界层理论，机翼举力线、举
力面理论，湍流理论，接合理论流体与实验流体，奠定了现代流体
力学气体动力学研究的基础
1910年瑞利和泰勒研究得出了激波的不可逆性
1933年泰勒和马科尔提出了圆锥激波的数值解
气体动力学基础_1
大学物理气体动理论

大学物理气体动理论


气体分子之间的相互作用力产生的势能， 由于气体分子之间的距离非常大，因此气 体分子的势能通常可以忽略不计。
分子动理论的基本假设
分子之间无相互作用力
气体分子之间不存在相互作用的力，它们之间只 存在微弱的范德华力。
分子运动速度服从麦克斯韦分布
气体分子的运动速度服从麦克斯韦分布，即它们 的速度大小和方向都是随机的。
分子碰撞的统计规律
分子碰撞的随机性
01
气体分子之间的碰撞是随机的，碰撞事件的发生和结果都是随
机的。
分子碰撞频率
02
单位时间内分子之间的碰撞次数与分子数密度、分子平均速度
和分子碰撞截面有关。
碰撞结果的统计规律
03
碰撞后分子的速度方向和大小的变化遵循一定的统计规律，可
以用概率密度函数来描述。
热现象的统计解释
大学物理气体动理论
• 引言 • 气体动理论的基本概念 • 气体动理论的基本定律 • 气体动理论的统计解释 • 气体动理论的应用 • 结论
01Biblioteka 引言主题简介气体动理论
气体动理论是通过微观角度研究气体 运动状态和变化的学科。它以分子运 动论为基础，探究气体分子运动的规 律和特性。
分子模型
气体动理论中，将气体分子视为弹性 小球，相互之间以及与器壁之间发生 弹性碰撞。通过建立分子模型，可以 更好地理解气体分子的运动特性。
对未来研究的展望
随着科学技术的发展，气体动理 论仍有很大的发展空间和应用前
景。
未来研究可以进一步探索气体分 子间的相互作用和气体在极端条 件下的行为，例如高温、高压或
低温等。
气体动理论与其他领域的交叉研 究也将成为未来的一个重要方向， 例如与计算机模拟、量子力学和
空气动力学(4学时)

空气动力学(4学时)


流动状态
(a) 流体成层状流动，称为层流状态。 (b) 流动呈高度非定常状态，非常紊乱，称为紊流态或湍流态。 雷诺发现，出现湍流状态的条件取决于组合量 Re= ρ U d/ μ， 式中ρ 为流体密度，U为管内平均流速，d为圆管直径，μ为流体的粘性系数。
雷诺数小，意味着流体流动时各质点间的粘性力占主要地位，流体各质点平行于管路内壁 有规则地流动，呈层流流动状态。雷诺数大，意味着惯性力占主要地位，流体呈紊流流动 状态，一般管道雷诺数Re＜2000为层流状态，Re＞4000为紊流状态，Re＝2000～4000 为过渡状态
;加速度
dV ∂V ds ∂V dV as = = = V =V dt ∂s dt ∂s ds
伯努利方程的推导过程（1）
应用线性动力的牛顿第二定律 质量 流体的重力
dV PdA−(P+dP)dA−Wsinθ = mV m = ρV = ρ dAds ds
W = mg = ρ gdA
代入，联立得
sin θ =dz/ds dz dV -dpdA - ρ gdAds = ρ dAdsV ds ds
对流层顶高度为11km或36089ft， 对流层内标准温度递减率为，每增 加1000m温度递减6.5°C，或每增 加1000ft温度递减2°C。从11km到 20km之间的平流层底部气体温度 为常值。
●国际标准大气表
大气环境介绍——高度的表示
绝对高度（True Altitude） 相对海平面高度 真实高度（Absolute Altitude）相对地面的高度 压力高度（Pressure Altitude）相对标准气压平面的高度
空气动力学
1.空气的物理性质、状态参数和状态方程 2.音速、马赫数、流管、流线的概念 3.低速流体流动的基本规律 4.高速流体流动的基本规律 5.低速和高速流体流动的区别
§8-2滞止参数、声速、马赫数16015

§8-2滞止参数、声速、马赫数16015

u M c 1.5 299.33 449(m/s)
三、气体动力学函数
气体动力学函数：我们在应 用气体动力学的知识去分 析、研究、计算有关工程 上的问题时，在一些公式 中其速度系数λ往往成几 种常见的组合形式出现， 叫做气体动力学函数。
每个函数用一个符号代表。
把各函数随速度系数变化的 数值计算出来列成数值表， 运用这种函数及其数值表 就可将公式大大简化，而 且使计算工作变得十分简 便。
（c） t3=t+dt
u·dt u·dt
p+dp
ρ+duρ △M c
(c-u)·t (c-u)·dt
二、声速、马赫数和速度系数
2
滞 止
式在中绝：热无摩擦的气流中，各段 面i的能0反cc滞全量0映止部。了k参能断kRR气T数量面T0流是，滞包kp不止kp0含p则变参00热反的数能映，可在机根T0内、械据
一、滞止参数
1 () T 1 k 1 2
T0
k 1
三种 常用 的气 体动
()
p
(1
k
1
2
)
k k 1
p0 2 k 1
力学
函数
4 ()
(1
k
1
2
)
1 k 1
0
k 1
由绝热过程方程式有：
p0 p
0k k
代将将入式Ccp2 pkk0k
pR 1 (1
代k 入1代MT入02)kkTk1+得2vC2：p 得：
二、声速、马赫数和速度系数
【例8－2】气流的速度为 800m/s，温度为530℃， 等熵指数k=1.25，气体 常数R=322.8J/(kg·K)。 试计算当地音速与马赫 数。
气体动力学

气体动力学


3. 马赫数 Ma 气流的压缩性除了与气体的声速有关外，还与气流的速度大 小有关
V Ma = C
dp
气体微团的运动速度与 气体微团当地的声速之 比
dρ dp dρ 2 dV 等熵过程 − Ma ⋅ = −VdV = = ⋅ V ρ ρ ρ dρ
在绝能等熵流动中，气流速度相对变化量所引起的密度相对变 2 化量与 Ma 成正比
V h = h+ 2
∗
2
T k −1 2 = 1+ Ma T 2
滞止状态与实际状态在
T − S 图上的表示
T 1
*
点 1 代表气流被滞止之前的状 态，其静温为 T ，速度为 V 1 1
P* 1 V 1 2CP P1
2
T* 1
的长度应为 V 2Cp
1∗ 代表了气流的滞止状态， 点 代表了气流的滞止状态， * 其温度为 T ∗， 线段 1−1
k −1 k −1 ∗ ∗ k k p2 ∗ p2 ∗ ws = cpT 1− ∗ = h 1− 1 P 1 P∗ 1 1
反映气流总能量可以转化为机械功的比例大小
能量方程的应用 绝能流动中能量方程可表示为
1 2 p = p + ρV 2
∗
−wS = cp (T2 −T 1
)
若流动为绝热定熵流动则能量方程为式
k −1 k −1 ∗ ∗ p2 k p2 k ws = cpT∗ 1− ∗ = h∗ 1− ∗ 1 1 P P 1 1
dp = ρCdV
要具体计算声速还必须知道在微扰 动传播过程中的压强p和密度ρ 动传播过程中的压强p和密度ρ之 间的关系
第2章 一维定常流动的基本方程(Part4.临界状态和气体动力学函数)

第2章 一维定常流动的基本方程(Part4.临界状态和气体动力学函数)

2016/3/30
中国民航大学航空工程学院发动机系
8
气体动力学（Aerodynamics）
临界状态和临界参数
对于一个绝能等熵加速流动，
T
*
P
* * c T( ) *
出口截面马赫数等于 1 的喷管， 出口截面即为临界截面，它的 参数也是整个流管的临界参数 马赫数小于1的截面上的气流 状态参数、滞止参数和临界参 数的关系
2016/3/30
0.2 0 0.4 0.8 1.2 发动机系
气体动力学（Aerodynamics）
2016/3/30
中国民航大学航空工程学院发动机系
18
气体动力学（Aerodynamics）
2016/3/30
中国民航大学航空工程学院发动机系
19
( Ma ＜1 )
P T( c ) Pcr
cr
Tcr ( ccr )
s
滞止状态、临界状态和实际状态
2016/3/30
中国民航大学航空工程学院发动机系
9
气体动力学（Aerodynamics）
速度系数：λ
V ccr
——无量纲的速度，气流速度与临界声速之比
思考：已经定义了Ma，为什么还要引入速度系数λ？
2 p A q z k 1 p A f
qm AV
2016/3/30
中国民航大学航空工程学院发动机系
22
气体动力学（Aerodynamics）
2016/3/30
中国民航大学航空工程学院发动机系
23
气体动力学（Aerodynamics）
2016/3/30
中国民航大学航空工程学院发动机系
24
空气动力学公式

空气动力学公式


q T
dh Tds vdp
\* MERGEFORMAT (2-13)
对于一个封闭均匀的系统，在可逆条件（并不一定绝热）下有：
de Tds pdv
对于一般的热力学状态，有：
ds cV dT p dv T T v
\* MERGEFORMAT (2-14)
空气动力学基本公式
1 标量场与矢量场
1.1 哈密顿算子
V V V V x y z V Vx Vy Vz x y z
\* MERGEFORMAT (1-1)
V Vx Vy Vz x y z
\* MERGEFORMAT (1-2)
\* MERGEFORMAT (3-17) 速度系数形式为：
k arc tan

2
1 / k 2 arc tan k 2 1 / k 2
\* MERGEFORMAT (3-18) 气流偏转角为：
Ma2 Ma1

* 2 1 0 1
1
a*
2 RT0 1
\* MERGEFORMAT (3-5) 定义速度系数：
λ
1 Ma 2 u a* 2 1 Ma 2
Ma
2λ 2 1 1 λ 2
\* MERGEFORMAT (3-6) 定义气体动力学函数

\* MERGEFORMAT (2-19) \* MERGEFORMAT (2-20)
T / p T
1 /
const
/ 1
/ p const
3 激波与膨胀波
3.1 声速与滞止参数、临界参数
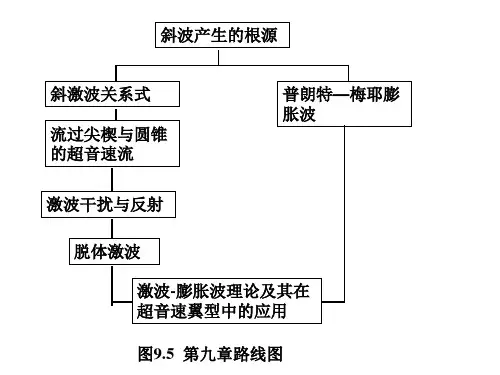
空气动力学chapter9(4)讲解

空气动力学chapter9(4)讲解


• 两左行激波干扰
两同向激波相交形成一更强的激波CD, 同时伴随一个弱反 射波CE。这一反射波是必须的，以调节保证滑移线CF分 开的4区和5区速度方向相同。
9.5 DTACHED SHOCK WAVE IN FRONT OF A BLUNT BODY 钝头体前的脱体激波
Shock detachment distance ：激波脱体距离；Sonic line:音速线
(M ) 1 tan1 1 (M 2 1) tan1 M 2 1 （9.42)
1
1
因此，（9.40)的积分可以表示为：
(M2 ) (M1)
（9.43)
(M2 ) (M1)
（9.43)
(M ) is given by Eq. (9.42) for a calorically perfect gas.
反射波后的特性没有理论方法求解，可采用数值解法求解。
马赫反射图示
•右行、左行激波干扰 (Intescetion of right- and left-running shock waves) A:左行波 B:右行波 C:激波B的折射波
D:激波A的折射波 EF:滑移线
折射：Refracted 滑移线：Slip line
9.7 SHOCK-EXPANSION THEORY : APPLICATIONS TO SUPERSONIC AIRFOILS 激波——膨胀波理论及其对超音速翼型的应用
例1 平板翼型：
图9.26中,平板翼型上表面为前缘处膨胀波后的压强p2， 下表面为前缘处斜激波后的压强 p3， p3 >p2，因此平板翼 型受到合力R’的作用，可分解为升力L’和阻力D’：
（1.8)
第八章 一元气体动力学基础-终1

第八章 一元气体动力学基础-终1


d


du dA 0 u A
二、可压缩气体的能量方程式
理想流体做定常流动，沿流线的积分方程为：
W dp u2 fds C 2
忽略质量力，力的势函数 W 0 则：
并且等熵气流不计摩擦

dp
u2 C 2
fds 0
——理想气体一元恒定流的能量方程
微分得：
当地音速
（4）空气
T 288K
c 340m / s
二、马赫数Ma
1．定义： 即流体速度u与介质中音速C之比。
V Ma c
在流速一定的情况下，当地声速越大，Ma越小，气体压缩性就越小。 例：在风洞中，空气流速u＝150 m/s，其温度为25℃，试求其马赫数Ma？
解;当空气为25℃，其声速为：
密度ρ 温度为T
活塞突然以微小速度向右运动 dv 微弱的扰动以速度c向右传播 波后气体处于受扰动状态：
p dp
d
T dT
（1）受到扰动的气体在dt时间前和dt时间后的质量守恒方程式 dt时间前气体的质量为：
m V cAdt
d )(c du ) Adt
cd cd du ＝ d
（2）等温过程
RT p
代入积分得
1
v2 RT ln p c 2
（3）绝热过程
可压缩理想气体在等温过程 中的能量方程
理想气体的绝热过程→等熵过程
p

k
c
k
cp cv
——绝热指数
代入积分得
k p v2 c k 1 2
证明：
或
1 p p v2 c k 1 2
增大
流体力学 第九章 第二节

流体力学 第九章 第二节



d(
2
k
const， ) dp
p

k

k
k
pd

k 1
0
dp p k为绝热指数 C k d p 代入状态方程 RT ，得

C kRT 从上式可以看出，声速仅取决于气体的物理性质和绝对温度。 例如在温度t 5℃，氢气中声速约为1280m / s，空气中的声速 约为335m / s。
p0 p
u 2
等熵滞止时，u2 0，p2 p0，上式变为
k 1 2 k u k p p0 1 2 k 1 p 化简后，得
p0 k 1 u 2 1 p 2 k p 3、滞止密度 p0 0 RT0

上式变为： C2 u2 const k 1 2 当u 0，C Cmax 当气流速度由零增大到umax 过程，必然存在一个速度刚好 等于声速，此时对应的声速称为临界声速，用Cc 表示。
Cc2 Cc2 1 2 C2 u2 k umax C pT0 RT0 k 1 2 k 1 2 2 k 1 由上式得临界声速 2 k 1 Cc kRT0 umax k 1 k 1 在绝热过程中，随速度u变化，C变化，Cc不变， 只与气流的总温有关，总温不变，Cc不变。 u 速度系数 Cc 与M相比： （ ）容易计算，在绝能的情况下为常数； 1 （2）u umax ，C 0，M ，max k 1 k 1

因
d

为无穷小量，与1相比可忽略不计，则
dp C d
dp 代表气体的可压缩性。 d dp 大，气体不易压缩； d dp 小，气体易压缩。 d 理论上，在绝对刚体介质中微弱扰动的传播速度无穷大。 声速大小表征介质可压缩的难易程度。

第九章气体动力学基础

第九章气体动力学基础第九章气体动力学基础一、微弱扰动在气流中的传播1、音速和马赫数音速是微弱扰动在流场中的传播速度。

微弱扰动通常是流场中某个位置上的压强产生了微小的变化。

在不可压缩流动中，任何扰动总是立即传播到整个流场，但是在可压缩流里，不是在任何情况下都能传播到整个流场，微弱扰动在流场中是按一定的速度传播的，这个速度就是音速。

一个直圆管，里面充满了压强为p、密度为ρ、温度为T的静止气体。

活塞以dv速度运动，将压缩(或膨胀)最相邻的气体层，致使那层气体的压强升高(或降低)、温度升高(或降低)。

这层气体又去压缩另外的气体层。

这样将在管道内形成微弱扰动的压缩波(或膨胀波)，波面的传播速度假设为c，气体本身也将随活塞一起运动，其运动速度将和活塞的运动速度一致，是dv。

请注意，压缩（或膨胀）波的波面速度与活塞(因而是气体)的运动速度不一致的！现在来推导音速公式。

由于微弱扰动在管道里的传播是一个非定常运动，因此假设研究者和波面一同运动。

这样，波面是相对静止的，而波前气流速度为c，波后气流速度为c-dv，同时压强密度和温度分别由p、ρ和T升到p+dp、ρ+dρ和T+dT。

在波面附近取一个微元体，有连续方程：动量方程：因为我们讨论的是微弱扰动，故高阶项可忽略。

把dv消去，得到音速为弱扰动的过程可以认为是一个等熵过程，即有对于微弱扰动，其热力学过程接近于绝热的可逆过程，即等熵过程。

对完全气体，(1)音速的的大小是和流体介质有关：可压缩性大的介质，微弱扰动传播的速度慢、音速就小。

在20度的空气中，音速为343(m/s)；在20度的水里，音速为1478(m/s)。

(2)音速是状态参数的函数。

在相同介质中，不同点的音速也不同。

提到音速，总是指当地音速。

(3)同一气体中，音速随气体温度的升高而升高马赫数的定义在音速定义后，可以定义马赫数1)马赫数是判断气体压缩性的标准, 它是个无量纲量,也是气体动力学的一个重要参数(2)按马赫数，可以将气流分成亚音速、音速和超音速流动。

气体动力学理论


分子平均碰撞频率和平均自由程
基本观念： 宏观现象是微观过程统计平均的结果
§19.1
统计方法的一般概念
要点： 1. 复习统计方法的一些基本概念
2.
推导理想气体 p、T
公式
一、统计规律 —— 大量偶然事件整体所遵从的规律
不能预测， 多次重复（大量出现）
例： 伽尔顿板实验
(演示实验室)
每个小球落入哪个槽是偶然的
自由质点 不计重量 分子 弹性质点 分子
分子
器壁
2.统计性假设（平衡态下） （1)分子处于容器内任一位置处的概率相同（均匀分布）
分子数密度
N n V
处处相等
（2)分子沿各方向运动的概率相同 • 任一时刻向各方向运动的分子数相同
N x N y Nz ,
N x N x
• 分子速度在各个方向分量的各种平均值相同
统计规律 个体规律简单叠加
3. 与宏观条件相关 如： 伽尔顿板中钉的分布， 4. 伴有涨落
二. 统计规律的数学形式——概率理论
1. 定义：
总观测次数 A 出现的概率
N
NA W A l in N N
出现结果 A 次数
NA
2.意义：描述事物出现可能性的大小
例如： 违反能量守恒定律的事件不可能发生
四、理想气体的压强公式
从公式推导中领会经典气体运动理论的典型思想方法： 1)提出模型 2)统计平均 3)建立宏观量与微观量的联系 4)阐明宏观量的微观实质
1.建立模型－理想气体
宏观模型： 严格遵守三条实验定律
微观模型： 无规运动的弹性质点的集合
质点 理想气体 分 子 不计大小 分子 器壁 分子 除相撞外无 相互作用 弹性碰撞
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

0.658
查表得 0.406, () 0.907
故总压为
p p 4.12 10 5 4.54 10 5 牛顿 米2
() 0.907
三、与冲力有关的气动函数 应用动量方程计算管壁受力时，往往出
现冲力J dm C pA 这个物理量，它与
dt
速度系数 也有某种函数关系。下面就


dm dt

a临


k 1 a临
2k

k 1 2k
a临


dm dt
k 1 2k
a临

2k k 1


1


k k

1 1



dm dt
k 1 2k a临


1


•令
Z（） 1
•
最后写成
J

k 1 2k
dm dt
q() (4)当气流的总压和总温发生变化时， 和 流量就没有一一对应的关系了。在某种情q(况) 下，可能会出现流量增大，而流通能力
反而减小的现象。
• 公式中的流量是用总压来表示的，有时为了 测量和计算方便，也需要用截面上的静压来表 示流量。这时，流量公式可写为
dm B p Aq() B p A q()
dm B p Aq()
dt
T
式中
B
k(
2
k 1
) k 1
R K 1
• 对于给定的气体(k及R一定)，B 是个常数。
对于空气，k=1.4，R=287．06焦耳／千
克·开，B =0.0404；对于燃气，
当 k=1.33，R=287．4焦耳／千克·开时
B =0.0397；当k=1.2，R=320焦耳／千

q()
2
k 1
• 所以
C A临 q() 临C临 A
• q() 仅是 数的函数，所以它也是气动函
数。
• 由（2-3-25a）式可知，气动函数q() 就是
相对密流，它也等于临界截面与所研究截
面的面积比。当k=1.4时，q() 随 数的变
化情形，如图2-3-10所示。由图可见，
C 临C临

临C临 Aq()
(1)
而
临 （1 k 1）k11 (
2
1
) k 1

k 1
k 1
•即
临

（
2
1
）k 1
k 1

p RT
(
2
1
) k 1
k 1
(2)
而
C临 a临
2 kRT k 1
(3)
将(2)和(3)式代入(1)式整理后得质量流量
一、气流静参数与总参数之比的气动函数
• 气流的总参数与静参数之比可以写成数的 函数：
T 1 k 1M 2
T
2
p

(1

k
1
M
2
)
K K 1
p
2


(1
k
1M
2
)
1 K 1

2
• 为了画曲线和制表方便，需把上式中的数 换成数，为此，将前式
2 2
M 2 k 1
1 k 1 2
p1 T1
A1q()
p1 T1
A2q(2 )
由于是绝能流动 T1 T2
又是非等熵流动 所以
p2 0.94 p1
q()
p 1
p 2
F1 F2
q()
1 0.94

1 2.5
q(1
)

0425
q(1
)
查表知 0.85时，q() 0.9729
克·开时，B =0.0362。
•
在气体动力学和喷气发动机原理中，
用相对密流和总参数表示的流量公式来分
析问题和计算流量是很方便的。
• 从流量公式可知，流管中任一截面所通 过的流量大小，与该截面的面积、总压、 相对密流成正比，与总温的平方根成反 比。据此还可得到如下重要结论。
(1)在气流的总压和总温保持不变的情 况下，流过任一截面(即F一定)的流量q() 与dm成正比，也就是说，q() 与 dm有 一一dt对应的关系。因此，在总压d和t 总温
即
C A临 临C临 A
• 因为临界截面是流管中的最小截面积， 所以临界截面的密度最大，也就是说， 临界截面的单位面积流量最大。相对 密流一般小于1。它的大小，可用来说 明任一截面的密流与最大密流接近的 程度，即说明该截面的流通能力的大 小。相对密流越接近1，说明截面流通 能力越大。临界截面的相对密流等于1。
截面积。即亚音速时，流管截面减小，气 流加速；反之流管截面积增大，气流减速。
• 当气流为超音速时( >1)，由图2—3—10可 见，因q() 随 数的增大而减小，故速度增
大时，必须相应地增大流管截面积，即超音速 时，流管截面增大，气流加速；反之，流管截 面积减小，气流减速。
• 当 =1时，q()达到最大值，q() =1，相应
不同 数下，这三个函数的大小还与气
体的性质有关。对于空气来说，k=1.4，
当 =1时， ()=0．8333， () =0．5828
， () =0．6340。同理，根据静参数与总参 数之比的数值，也可以查出相对应
的 数和M数大小。
• [例2—3—5]用风速管测量空气流中一 点 的 总 压 p =9 ． 81x 牛 顿 ／ 米 ， 静 压 p 8.44 10 4 牛顿 / 米2，用热电偶测得 该点气流的总温 T 400K，试求该点气 流速度 C 。
dt
T
() T
•令
y() q() ()
•则
dm B p Ay()
dt
T
• y() 随 数的变化情形，如图2—3—10
所示。由图中看出，y()随 数增大而增 大，当 接近最大时，y() 趋于无穷大，
• y()的数值可由气动函数表中查到(见附 录)。
k 1
• 代入上列诸式，化成数的函数，并分别
以， () ， () ， () 来表示；
• 可得
() T 1 k 1 2
T*
k 1
()
p p*

(1

k
1 2
)
k k 1
k 1
()


(1
k

1
2
)
k k 1
*
k 1
• 根据每一个数，把， ()、 ()、 ()三个函 数的数值计算出来，列成表格(见附录)。
使用时，根据气流的 数(或M数)，就可以 查出与 数相的静参数与总参数之比的数
值。以此为基础，如已知总参数，就可以
求出静参数；已知静参数，就可求出总参
数。
• 显然三个函数 () 、 () 、 () 之间的关系 是：
•
()

*

T* T
.
P P*

() ()
在 =0和 最大
k 1 k 1
时，q()
=0时
=1 时，q() =1，达到最大。这说明，
当 =1时，单位面积上通过的流量最
大。q() 的数值可由气动函数表中查到
（见附录）。
• 应用相对密度 q() ，可以直接根据总参数计 算流量。因为
dm dt

AC

(临C临 ) A

3.11105
牛顿
米2
二、与流量有关的气动函数
•
由流量公式知
dm dt

A临临C临，流管任一
截面和临界截面的密度（即单位面积流
量）分别为：
dm
dm
C
dt A
和临C临
dt A临
• 任一截面单位面积上的流量与临界截面 单位面积流量之比，也就是任一截面的密 流与临界截面密流之比，称为相对密流。 又叫做无量纲密流。
• 当k=1.4时，函数 ()、 ()和 ()随 数的
变化曲线如图2—3—9所示。从图中可看
出 ， 在 任 一数 下 ， 都 有 一 个 确 定 的， () 、 ()、 ()数值相对应。当 =0
时， () = () =1； 数增大时，三个函数
都减小；当 = 最大时， ()= () = () =0
因此
q(2 ) 0.425 0.9729 0.414
再查表得 2 0.27, (2 ) 0.9579 所以
p2 p2 (2 ) 0.94 p1 (2 ) 0.94 2.942 10 5 0.9579
2.649 10 5 牛顿 米2
的截面积应是流管的最小截面积，即临界截面
( =1的截面)必须是流管中的最小截面，必
须注意，这个结论反过来说并不一定正确，即 流管的最小截面并不一定是临界截面。要将气 流等熵绝能地由亚音速到超音速，管道必须做 成先收敛后扩散的形状，即所谓缩扩管。
• (3)在一维定常管流中，用临界截面的参数 计 算 流 量 最 为 方 便 ， 因 为 临 界q(截) 面 的 =1．
保持不变的情况下，相对密流 的大小， 反映流量的大小。
• (2)在气流的总压和总温保持不变的情况下， 要使通过同一管道中不同截面的流量相 等，
则必须使乘积A 保持q为(常) 数。由此可知；
当气流为亚音速时( <1)时，由图2—3— 10可见，随着 数的增大， 也跟q(着)增大，
为了保持流量不变，必须相应地减小流管
a临