气体动力函数表
- 格式：doc
- 大小：373.00 KB
- 文档页数：3
文档推荐
-
Excel常用的函数计算公式大全页数:3
-
EXECL计算公式自动计算页数:2
-
员工考勤统计表-函数自动统计页数:2
-
Excel函数计算公式大全(完整)页数:14
-
考勤表(带公式自动计算)页数:2
下载文档原格式
合集下载
气体动力学基础PPT课件
气体动力学基础_1
23
第二章 一维定常流的基本方程
§2.1 应知的流体力学基本概念
• 无限多个连续分布的流体微团 组成的连续介质的假设（
Euler明确，1752）。而非分子论。适用于l/L<1/100，例
如100公里以下的大气与飞行器
• 一维定常流 1-D Steady flow，流线 Streamline，
3
第一章 绪论
§1.1 气体动力学的涵义
气体动力学是
➢ 流体力学的一个分支，在连续介质假设下，研
究与热力学现象有关的气体的运动规律及其与
相对运动物体之间的相互作用。
➢ 气体在低速流动时属不可压缩流动，其热力状
态的变化可以不考虑；但在高速流动时，气体
的压缩效应不能忽略，其热力状态也发生明显
的变化，气体运动既要满足流体力学的定律，
学科名 Discipline 流体力学 Fluid Dynamics 空气动力学 Aerodynamics 气体动力学 Gas Dynamics
主要研究范围 Primary Scope
不可压缩流体动力学 Incompressible Fluid Flow
不可压缩＋可压缩流体动力学 Incom-＋Com-pressibleLeabharlann 解析解，螺旋桨理论，飞机设计
1904-20年代，普朗特Prandtl（德）的普朗特－迈耶流动理论，（超音
速膨胀波和弱压缩波），风洞技术，边界层理论，机翼举力线、举
力面理论，湍流理论，接合理论流体与实验流体，奠定了现代流体
力学气体动力学研究的基础
1910年瑞利和泰勒研究得出了激波的不可逆性
1933年泰勒和马科尔提出了圆锥激波的数值解
气体动力学基础_1
§8-2滞止参数、声速、马赫数16015
u M c 1.5 299.33 449(m/s)
三、气体动力学函数
气体动力学函数：我们在应 用气体动力学的知识去分 析、研究、计算有关工程 上的问题时，在一些公式 中其速度系数λ往往成几 种常见的组合形式出现， 叫做气体动力学函数。
每个函数用一个符号代表。
把各函数随速度系数变化的 数值计算出来列成数值表， 运用这种函数及其数值表 就可将公式大大简化，而 且使计算工作变得十分简 便。
（c） t3=t+dt
u·dt u·dt
p+dp
ρ+duρ △M c
(c-u)·t (c-u)·dt
二、声速、马赫数和速度系数
2
滞 止
式在中绝：热无摩擦的气流中，各段 面i的能0反cc滞全量0映止部。了k参能断kRR气T数量面T0流是，滞包kp不止kp0含p则变参00热反的数能映，可在机根T0内、械据
一、滞止参数
1 () T 1 k 1 2
T0
k 1
三种 常用 的气 体动
()
p
(1
k
1
2
)
k k 1
p0 2 k 1
力学
函数
4 ()
(1
k
1
2
)
1 k 1
0
k 1
由绝热过程方程式有：
p0 p
0k k
代将将入式Ccp2 pkk0k
pR 1 (1
代k 入1代MT入02)kkTk1+得2vC2：p 得：
二、声速、马赫数和速度系数
【例8－2】气流的速度为 800m/s，温度为530℃， 等熵指数k=1.25，气体 常数R=322.8J/(kg·K)。 试计算当地音速与马赫 数。
三、气体动力学函数
气体动力学函数：我们在应 用气体动力学的知识去分 析、研究、计算有关工程 上的问题时，在一些公式 中其速度系数λ往往成几 种常见的组合形式出现， 叫做气体动力学函数。
每个函数用一个符号代表。
把各函数随速度系数变化的 数值计算出来列成数值表， 运用这种函数及其数值表 就可将公式大大简化，而 且使计算工作变得十分简 便。
（c） t3=t+dt
u·dt u·dt
p+dp
ρ+duρ △M c
(c-u)·t (c-u)·dt
二、声速、马赫数和速度系数
2
滞 止
式在中绝：热无摩擦的气流中，各段 面i的能0反cc滞全量0映止部。了k参能断kRR气T数量面T0流是，滞包kp不止kp0含p则变参00热反的数能映，可在机根T0内、械据
一、滞止参数
1 () T 1 k 1 2
T0
k 1
三种 常用 的气 体动
()
p
(1
k
1
2
)
k k 1
p0 2 k 1
力学
函数
4 ()
(1
k
1
2
)
1 k 1
0
k 1
由绝热过程方程式有：
p0 p
0k k
代将将入式Ccp2 pkk0k
pR 1 (1
代k 入1代MT入02)kkTk1+得2vC2：p 得：
二、声速、马赫数和速度系数
【例8－2】气流的速度为 800m/s，温度为530℃， 等熵指数k=1.25，气体 常数R=322.8J/(kg·K)。 试计算当地音速与马赫 数。
气体动力学
表明：气流速度v的变化，总是与参数ρ、p、T 的变化相反。v沿程增大，ρ、p、T必沿程减小 ，v沿程减小，ρ、p、T必沿程增大。 将上面3个式子代入连续性微分方程式
c 1 sin v Ma
例1. 飞机在温度为20℃的静止空气中飞行，测得 飞机飞行的马赫角为40.34º，空气的气体常数 R=287J/（kg〃K），等熵指数k=1.4，试求飞机的 飞行速度。 解：飞机飞行的马赫数
Ma 1 1 1.54 sin sin40.34
当地声速 c kRT 1.4 287 273 20 343.11m/ s
二、马赫数
气体流速v与当地声速c之比，称为马赫数，以 Ma表示 v Ma c 根据它的大小，可将气体的流动分为： Ma＜1，即v＜c，亚声速流动； Ma＝1，即v＝c，声速流动（Ma≈1，为跨声速流 动）； Ma＞1，即v＞c，超声速流动。
微弱扰动波在不同流场中的传播
4c v=0 2c c o 3c 3c 4c v <c c o 2c
由等熵过程能量方程，得
k p1 v1 k p2 v2 k 1 1 2 k 1 2 2
2 2
解得
v 2 279.19m / s
Qm 2 A2 v 2 0.74kg/ s
§9.3 气体一维恒定流动的参考状态
常见的参考状态：
一、滞止状态 二、临界状态 三、极限状态
可压缩流体
气体动力学就是研究可压缩气体运动规律及 其在工程中应用的科学。
§9.1 声速与马赫数
§9.2 气体一维恒定流动的基本方程 §9.3 气体一维恒定流动的参考状态
§9.4 气流参数与通道截面积的关系 §9.5 喷管
§9.1 声速与马赫数
气体动力学基础2(1)
u2 p dp q de d dh d 2
对于绝热流动
q 0
或
u hC 2
2
u2 C pT C 2
一元定常绝热流动的能量方程在绝热流动中，
单位质量气体的焓与动能之和保持不变。
u2 C pT C 2
kR 1.4 287 Cp 1004.5 J / ( Kg K ) k 1 1.4 1 u2 C pT C pT0 2 由此解出气体的出流速度为：
u
2C p T0 T 2 1004.5 300 290
141.74 m/s
9.1 一元稳定可压缩流动的基本方程
1 dp dv v 0 ds ds
或
dp
或
dp
vdv 0
v2 d 0 2
上两式称为欧拉运动微分方程，或微分形式的伯努利方程。
或者：
2 kR u 2 umax T k 1 2 2
T u 1 T0 2c pT0
2
2 umax u2 c pT c pT0 2 2
u T u 1 1 T0 2c pT0 u max
2
2
对于等熵流动，有：
u2 1 2 0 umax
动力学的动量守恒定律
热力学方面的能量守恒定律 气体的物理、化学属性方面的气体状态方程 及 气体组元间的化学反应速率方程
气体输运性质(黏性、热传导和组元扩散定律)等
✽ 气体动力学的研究内容
①研究高速气体对物体(如飞行器)的绕流即外流问题，包括
正问题：给定物体的外形及流场边界、初始条件，求 解绕流流场的流动参数，特别是求出作用在物面上的 气动特性。 反问题：给定流场的一部分条件和需要达到的气动指 标(如高升阻比)，求解最佳物形。
空气动力学与热学基础——第十七讲
相对密流可写成速度系数的函数，具体推
导如下。
C C
临临
临
C C
临
（1
k
1
1）2 k1
k 1
k 1 1
(1
) k 1
k 1
(k
1)
1 k 1
(1
k
1
2
)
1 k 1
2
k 1
令
(k
1)
1 k 1
(1
k
1
2
)
1 k 1
q()
2
k 1ห้องสมุดไป่ตู้
所以
C A临 q() 临C临 A
q() 仅是 数的函数，所以它也是气动函数。
压p 8.44 10 4 牛顿 / 米2，用热电偶测得
该点气流的总温 T 400K，试求该点气流
速度 C 。
解：(2—3-23)式有 () p 8.44104 0.86
p 9.81104
由气动函数查得 =0.5025
气流速度
C a临
2k RT k 1
得
C 0.5025 2 1.4 287 .06 400 184 米 秒 1.4 1
B =0.0397；当k=1.2，R=320焦耳／千
克·开时，B =0.0362。
在气体动力学和喷气发动机原理中，
用相对密流和总参数表示的流量公式来分析
问题和计算流量是很方便的。
从流量公式可知，流管中任一截面所通过 的流量大小，与该截面的面积、总压、相 对密流成正比，与总温的平方根成反比。 据此还可得到如下重要结论。
第十七讲
气体动力学函数及应用
介绍气体动力学函数 定义及其应用
气体动力学函数的定义
空气动力学基本概念
1.2 声速和马赫数
声速
定义：指微弱扰动波在 流体介质中的传播速度
扰动压缩波 扰动膨胀波 声音是由微弱扰动压缩
波和膨胀波交替组成的 微弱扰动波
马赫数
定义：流场中某点处的气体流速与当地声速之 比即为该点处气流的马赫数：
M V a
完全气体：
V2
M2V a22
V2 2 2
kRT kk1cvT
ax ay az
aaxyvvddttddxyvvvvxyttxyvvvvttxxxyvvxy(v(vvvxxxxxxxxyy,,ddddyyxtxt,,vvzzvyv,yy,yxyttd)d)ddvyvtyytyxyvvzzxydvdddvztzztzvvzzxy azvdtdzvvztzvvtxzvz(vvxxxzz,ddyxt,vzvy,yztdd)vytyzvzz dvdzztvzz
1.3 热力学中的基本定律
状态方程、完全气体、内能和焓
状态方程： f(p ， ， T)0
完全气体： pRT 内能（完全气体）： uu(T)
焓值： h u p
p/ρ代表单位质量气体的压力能，故焓表示单位质量
气体的内能和压力能的总和 ； 对完全气体，焓只取决于温度。
热力学第一定律
外界传给一个封闭物质系统（流动着的气体微团是其 中之一）的热量等于系统内能的增量和系统对外界所 做机械功的总和 ：
统计平均速度 连续介质速度
VlimVi n n n limm
V
A0 A
气体状态方程
完全气体：模型气体，完全弹性的微小球粒，内聚力 十分微小（忽略），微粒实有总体积（忽略）
状态方程：压强、密度和温度之间的函数关系 完全气体的状态方程：
pRT
空气动力学公式范文
空气动力学公式范文空气动力学公式指的是描述物体在空气中受力和运动的数学公式。
在工程和物理学领域中，空气动力学公式被广泛应用于空气动力学研究、航空航天工程设计、汽车设计以及建筑设计等方面。
下面是一篇超过1200字的空气动力学公式范文，介绍了一些常见的空气动力学公式及其应用。
一、气体动力学理论基础在空气动力学研究中，气体动力学理论是非常重要的基础。
根据气体动力学理论，气体中的压力（P）、密度（ρ）和温度（T）之间存在一定的关系。
根据理想气体状态方程，可以得到如下公式：1.理想气体状态方程P=ρRT其中，P为气体的压力，ρ为气体的密度，R为气体的气体常数（通常为287 J/(kg·K)），T为气体的绝对温度。
2.理想气体压力与温度之间的关系P∝T根据理想气体状态方程，可以得出气体的压力与温度成正比。
二、飞行器气动力学公式在航空航天工程中，空气动力学公式用于描述飞行器受力和运动过程。
以下是一些常见的飞行器气动力学公式及其应用。
1.飞行器升力与气动系数之间的关系L = 0.5C_liftρV^2S其中，L为飞行器的升力，C_lift为升力系数，ρ为空气密度，V为飞行器的速度，S为飞行器的参考面积。
2.飞行器阻力与气动系数之间的关系D = 0.5C_dragρV^2S其中，D为飞行器的阻力，C_drag为阻力系数，ρ为空气密度，V为飞行器的速度，S为飞行器的参考面积。
3.飞行器侧向力与气动系数之间的关系Y = 0.5C_sideρV^2S其中，Y为飞行器的侧向力，C_side为侧向力系数，ρ为空气密度，V为飞行器的速度，S为飞行器的参考面积。
4.飞行器俯仰力矩与气动系数之间的关系M_pitch = 0.5C_pitchρV^2SC_bar其中，M_pitch为飞行器的俯仰力矩，C_pitch为俯仰力矩系数，ρ为空气密度，V为飞行器的速度，S为飞行器的参考面积，C_bar为平均气动弦长。
三、车辆空气动力学公式在汽车设计中，空气动力学公式用于描述汽车在行驶过程中受到的空气阻力。
第三章气体分子热运动速率和能量的统计分布律
麦克斯韦严谨的科学态度和科学研究方法是人类极其宝贵的精 神财富。
热学
14
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确？
（A） vp 是气体分子中大部分分子所具有的速率. （B） vp 是速率最大的速度值. （C） vp 是麦克斯韦速率分布函数的最大值.
（D） 速率大小与最概然速率相近的气体分子的比 率最大.
N
N
v
v f (v)dv
8kT
0
πm
v 1.60 kT 1.60 RT
f (v)
m
M
3）方均根速率 v2
o
v
v2
N
0
v2dN N
0
v2
Nf
N
(v)dv
v2 3kT m
热学
8
vp v v2
vrms
v2
3kT m
3RT M
v 1.60 kT 1.60 RT
m
M
vp
2kT m
为清楚起见 , 从正面来
观察。
铁钉
隔板
热学
28
统计规律和方法
伽尔顿板 再投入小球： 经一定段时间后 , 大量小
球落入狭槽。
分布情况：中间多，两边少。
重复几次 ，结果相似。
单个小球运动是随机的 , 大量小球运动分布是确定的。
大量偶然事件整体所遵 循的规律 —— 统计规律。
热学
小球数按空间 位置 分布曲线
v2
dN 4π(
m
)3
2
e
mv2 2 kT
v2
dv
N
2πkT
热学
5
反映理想气体在热动 平衡条件下，各速率区间 分子数占总分子数的百分
热学
14
讨论
麦克斯韦速率分布中最概然速率 vp 的概念
下面哪种表述正确？
（A） vp 是气体分子中大部分分子所具有的速率. （B） vp 是速率最大的速度值. （C） vp 是麦克斯韦速率分布函数的最大值.
（D） 速率大小与最概然速率相近的气体分子的比 率最大.
N
N
v
v f (v)dv
8kT
0
πm
v 1.60 kT 1.60 RT
f (v)
m
M
3）方均根速率 v2
o
v
v2
N
0
v2dN N
0
v2
Nf
N
(v)dv
v2 3kT m
热学
8
vp v v2
vrms
v2
3kT m
3RT M
v 1.60 kT 1.60 RT
m
M
vp
2kT m
为清楚起见 , 从正面来
观察。
铁钉
隔板
热学
28
统计规律和方法
伽尔顿板 再投入小球： 经一定段时间后 , 大量小
球落入狭槽。
分布情况：中间多，两边少。
重复几次 ，结果相似。
单个小球运动是随机的 , 大量小球运动分布是确定的。
大量偶然事件整体所遵 循的规律 —— 统计规律。
热学
小球数按空间 位置 分布曲线
v2
dN 4π(
m
)3
2
e
mv2 2 kT
v2
dv
N
2πkT
热学
5
反映理想气体在热动 平衡条件下，各速率区间 分子数占总分子数的百分
理想气体状态方程,范德瓦尔方程,维里方程
理想气体状态方程,范德瓦尔方程,维里方程理想气体状态方程指的是用于描述理想气体的受力性质的方程，它们是能够完全描述理想流体运动的最重要的三个方程，它们分别是范德瓦尔方程，维里方程和马氏势方程。
范德瓦尔方程，即流体力学的方程，由德国物理学家、流体力学家德卢斯·范德瓦尔（D.L.vonWaer）在1878年提出。
这个方程解决了流体不可压缩性，但具有弹性和流动性的条件。
它表示了流体总体上的平衡问题，并利用牛顿第二定律描述了流体小体上的动力学运动。
这个方程可以用拉格朗日——穆勒（Lagrange–Müller）形式来表示，即∇•[ρ（u•∇）u]=0其中ρ是流体的密度，u是流速的矢量。
右端的拉格朗日函数描述了流体的力学特性，即流体中的任意点的速度总是力学有序的，这与牛顿第二定律有关。
维里方程，又称为速度场方程，也被称为Pal von Karman method，是由法国物理学家吉恩·维里在1868年首次提出的，用于描述空气动力学的概念，是空气动力学的基础。
它的表达式是：∂u/∂t+u·∇u=1/ρ∇P-ΓK其中u是空气的速度矢量，P是压力，ρ是空气的密度，K是Kelvin-Helmholtz张量，Γ是重力加速度。
马氏势的方程是由德国物理学家、力学家西雅图·马氏（X. vonMaucher）在1902年提出的，用来描述流体的热性质。
马氏势方程有一般形式和特定形式两类。
一般形式：T∇μ+μ∇T-T∇S=0其中T是温度，μ是熵，S是熵密度。
它表明，当温度发生变化时，熵会随之变化。
它还揭示了温度、熵和熵密度之间的关系，这在万有引力场动力学有所体现。
特定型马氏势方程：h=h(s,t)S=S(s,t)这两个方程将温度、熵和焓分别连接起来，可用来描述温度、熵和焓之间的改变。
总体而言，范德瓦尔方程、维里方程和马氏势方程是用于描述理想气体的三个最基本的方程。
它们分别是流体力学方程、速度场方程和马氏势方程。
FLUENT中实际气体性质模型(UDRGM)在大规模数值模拟中的应用
1 前言工程实际中遇到的各类流动问题，当工质热物理性质偏离理想气体时，需要应用实际气体性质进行求解，才能比较精确地反映流动特性。
例如在蒸汽透平低压部分，低压水蒸汽的性质与理想气体性质偏离较大，如采用理想气体性质进行求解，误差较大。
IAPWS-IF97标准中给出了计算水蒸汽气体性质的计算公式，但由于计算量很大，并不适合在大规模三维计算中直接采用。
因此有必要发展一种高效高精度的实际气体性质计算方法。
本文以水蒸汽实际气体的求解为例，利用FLUENT 软件所提供的实际气体模型（UDRGM ）实现了大规模复杂计算中水蒸汽实际气体性质的应用。
2 FLUENT 中的实际气体模型（UDRGM ）及实现FLUENT 软件中提供了实际气体性质计算的接口UDRGM (User Defined Real Gas Model)。
利用该接口，可以将水蒸汽性质表导入FLUENT 中，实现对水蒸汽实际气体性质的计算。
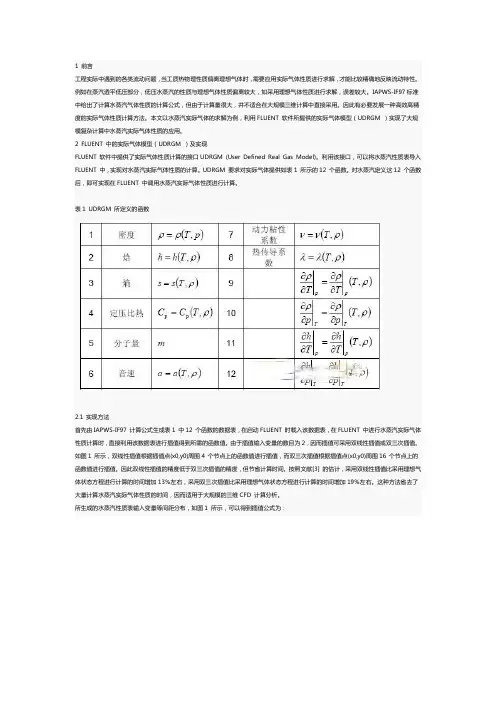
UDRGM 要求对实际气体提供如表1 所示的12 个函数。
对水蒸汽定义这12 个函数后，即可实现在FLUENT 中调用水蒸汽实际气体性质进行计算。
表1 UDRGM 所定义的函数2.1 实现方法首先由IAPWS-IF97 计算公式生成表1 中12 个函数的数据表，在启动FLUENT 时载入该数据表，在FLUENT 中进行水蒸汽实际气体性质计算时，直接利用该数据表进行插值得到所需的函数值。
由于插值输入变量的数目为2，因而插值可采用双线性插值或双三次插值。
如图1 所示，双线性插值根据插值点(x0,y0)周围4 个节点上的函数值进行插值，而双三次插值根据插值点(x0,y0)周围16 个节点上的函数值进行插值。
因此双线性插值的精度低于双三次插值的精度，但节省计算时间。
按照文献[3] 的估计，采用双线性插值比采用理想气体状态方程进行计算的时间增加13％左右，采用双三次插值比采用理想气体状态方程进行计算的时间增加19％左右。
这种方法省去了大量计算水蒸汽实际气体性质的时间，因而适用于大规模的三维CFD 计算分析。