数学物理方程讲义课后答案三四章 姜礼尚版本

数学物理方程第三版答案第一章． 波动方程§1 方程的导出。

定解条件1．细杆（或弹簧）受某种外界原因而产生纵向振动，以u(x,t)表示静止时在x 点处的点在时刻t 离开原来位置的偏移，假设振动过程发生的张力服从虎克定律，试证明),(t x u 满足方程()⎪⎭⎫ ⎝⎛∂∂∂∂=⎪⎭⎫ ⎝⎛∂∂∂∂x u E x t u x t ρ 其中ρ为杆的密度，E 为杨氏模量。

证：在杆上任取一段，其中两端于静止时的坐标分别为 x 与+x x ∆。

现在计算这段杆在时刻t 的相对伸长。

在时刻t 这段杆两端的坐标分别为：),();,(t x x u x x t x u x ∆++∆++其相对伸长等于 ),()],([)],([t x x u xxt x u x t x x u x x x ∆+=∆∆-+-∆++∆+θ令0→∆x ，取极限得在点x 的相对伸长为x u ),(t x 。

由虎克定律，张力),(t x T 等于),()(),(t x u x E t x T x =其中)(x E 是在点x 的杨氏模量。

设杆的横截面面积为),(x S 则作用在杆段),(x x x ∆+两端的力分别为x u x S x E )()(x u x x S x x E t x )()();,(∆+∆+).,(t x x ∆+于是得运动方程tt u x x s x ⋅∆⋅)()(ρx ESu t x =),(x x x x x ESu x x |)(|)(-∆+∆+利用微分中值定理，消去x ∆，再令0→∆x 得tt u x s x )()(ρx∂∂=x ESu () 若=)(x s 常量，则得22)(tu x ∂∂ρ=))((x u x E x ∂∂∂∂即得所证。

2．在杆纵向振动时，假设(1)端点固定，(2)端点自由，(3)端点固定在弹性支承上，试分别导出这三种情况下所对应的边界条件。

解：(1)杆的两端被固定在l x x ==,0两点则相应的边界条件为 .0),(,0),0(==t l u t u(2)若l x =为自由端，则杆在l x =的张力x ux E t l T ∂∂=)(),(|lx =等于零，因此相应的边界条件为x u∂∂|lx ==0 同理，若0=x 为自由端，则相应的边界条件为xu∂∂∣00==x (3)若l x =端固定在弹性支承上，而弹性支承固定于某点，且该点离开原来位置的偏移由函数)(t v 给出，则在l x =端支承的伸长为)(),(t v t l u -。

数学物理方程 李明奇主编 电子科技大学出版社2-3章部分习题答案习题2.14.一根长为L 、截面面积为1的均匀细杆，其x=0端固定，以槌水平击其x=L 端，使之获得冲量I 。

试写出定解问题。

解：由Newton 定律： tt x x Sdxu t x YSu t dx x SYu ρ=-+),(),(，其中，Y 为杨氏模量，S 为均匀细杆的横截面积，x u 为相对伸长率。

化简之后，可以得到定解问题为：⎪⎪⎩⎪⎪⎨⎧-==========)(|,0|0|,0|)/(0002L x I u u u u u a u Y u t t t L x x x xx xx tt δρρ。

习题2.23.设物体表面的绝对温度为u ，它向外辐射出去的热量，按斯特凡-波尔兹曼定律正比于4u ，即dSdt ku dQ 4=，设物体与周围介质之间，只有热辐射而无热传导，周围介质的绝对温度为已知函数),,,(t z y x ϕ，。

试写出边界条件。

解：由Fourier 热传导实验定律dSdt nuk dQ ∂∂-=1，其中1k 称为热传导系数。

可得dSdt u k dSdt n uk )(441ϕ-=∂∂-，即可得边界条件：)(441ϕ--=∂∂u k k nus。

习题2.34.由静电场Gauss 定理⎰⎰⎰⎰⎰⋅=⋅VsdV dS E ρε01，求证：0ερ=⋅∇E ，并由此导出静电势u 所满足的Poisson 方程。

证明：⎰⎰⎰⎰⎰⎰⎰⎰⋅=⋅=⋅VVsdV dV divE dS E ρε01，所以可以得到：0ερ=divE 。

由E divE ⋅∇=与u E -∇=，可得静电势u 所满足的Poisson 方程：02ερ-=∇u 。

习题2.42.求下列方程的通解：（2）：;032=-+yy xy xx u u u （5）：;031616=++yy xy xx u u u 解：（2）：特征方程：03)(2)(2=--dxdydx dy 解得：1-=dx dy 和3=dxdy。

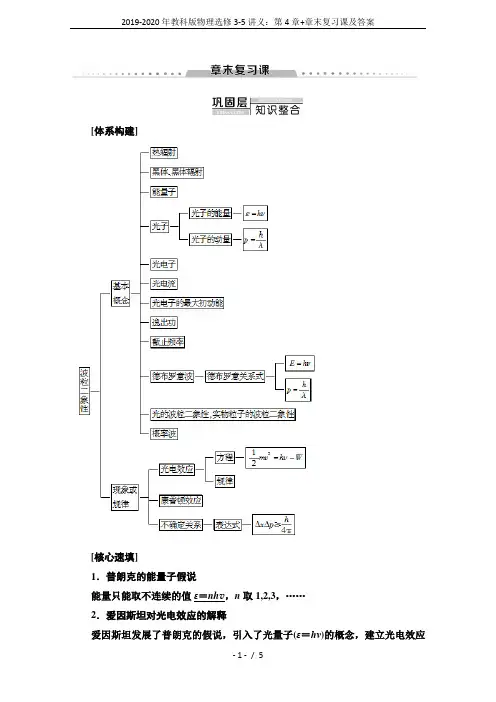
[体系构建][核心速填]1．普朗克的能量子假说能量只能取不连续的值ε＝nh v，n取1,2,3，……2．爱因斯坦对光电效应的解释爱因斯坦发展了普朗克的假说，引入了光量子(ε＝hν)的概念，建立光电效应方程hν＝12m v 2＋W ，以解释光电效应现象． 3．康普顿效应X 射线通过物质散射后波长变长的现象，称为康普顿效应．利用光的波粒二象性(ε＝hν，p ＝h λ)及光在与其他物质相互作用过程中的能量守恒、动量守恒，可对康普顿效应作出解释．4．光的波粒二象性 实验表明光在传播过程中，如干涉、衍射中显示出波动性；而在与物质的相互作用中，如康普顿散射、光电效应中表现出粒子性．光的本质是波动性和粒子性的统一，称为光的波粒二象性．光是一种概率波．5．德布罗意假说 电子等实物微粒像光子一样也具有波粒二象性．德布罗意波的波长由λ＝h p 确定．氢原子中电子在各处出现的概率可形象地用“电子云”来表示．6．不确定关系如果以Δx 表示粒子在x 方向上的位置不确定量，以Δp x 表示相应的动量不确定量，那么Δx ·Δp x ≥h 4π.运用光电效应方程进行计算．求解光电效应问题的关键在于掌握光电效应规律，明确各概念之间的决定关系，准确把握它们的内在联系．1．决定关系及联系2．“光电子的动能”可以是介于0～E km 的任意值，只有从金属表面逸出的光电子才具有最大初动能，且随入射光频率增大而增大．3．光电效应是单个光子和单个电子之间的相互作用产生的，金属中的某个电子只能吸收一个光子的能量，只有当电子吸收的能量足够克服原子核的引力而逸出时，才能产生光电效应．4．入射光强度指的是单位时间内入射到金属表面单位面积上的光子的总能量，在入射光频率ν不变时，光强正比于单位时间内照到金属表面单位面积上的光子数，但若入射光频率不同，即使光强相同，单位时间内照到金属表面单位面积上的光子数也不相同，因而从金属表面逸出的光电子数也不相同(形成的光电流也不相同)．【例1】(多选)如图所示是现代化工业生产中部分光电控制设备用到的光控继电器的示意图，它由电源、光电管、放大器等几部分组成．当用绿光照射图中光电管阴极K时，可发生光电效应，则以下说法中正确的是()A．增大绿光的照射强度，光电子的最大初动能增大B．增大绿光的照射强度，电路中的光电流增大C．改用比绿光波长大的光照射光电管阴极K时，电路中一定有光电流D．改用比绿光频率大的光照射光电管阴极K时，电路中一定有光电流BD[光电子的最大初动能由入射光的频率决定，选项A错误；增大绿光的照射强度，单位时间内入射的光子数增多，所以光电流增大，选项B正确；改用比绿光波长更大的光照射时，该光的频率不一定满足发生光电效应的条件，故选项C错误；若改用频率比绿光大的光照射，一定能发生光电效应，故选项D正确．]1．现用某一光电管进行光电效应实验，当用某一频率的光入射时，有光电流产生．下列说法正确的是()A．保持入射光的频率不变，入射光的光强变大，饱和光电流变大B．入射光的频率变高，饱和光电流变大C．入射光的频率变高，光电子的最大初动能不变D．保持入射光的光强不变，不断减小入射光的频率，始终有光电流产生A[产生光电效应时，光的强度越大，单位时间内逸出的光电子数越多，饱和光电流越大，说法A正确．饱和光电流大小与入射光的频率无关，说法B错误．光电子的最大初动能随入射光频率的增加而增加，与入射光的强度无关，说法C错误．减小入射光的频率，如低于极限频率，则不能发生光电效应，没有光电流产生，说法D错误．]1的两种学说是相互对立的，都企图用一种观点去说明光的各种“行为”，这是由于传统观念的影响，这些传统观念是人们观察周围的宏观物体形成的．2．波动性和粒子性在宏观现象中是相互对立的、矛盾的，但对于光子这样的微观粒子却只有从波粒二象性的角度出发，才能统一说明光的各种“行为”．3．光子说并不否认光的电磁说，按光子说，光子的能量ε＝hν，其中ν表示光的频率，即表示了波的特征，而且从光子说或电磁说推导电子的动量都得到一致的结论．可见，光的确具有波动性，也具有粒子性．【例2】(多选)关于光的波粒二象性的说法中，正确的是()A．一束传播的光，有的光是波，有的光是粒子B．光子与电子是同样的一种粒子，光波与机械波是同样的一种波C．光的波动性不是由于光子间的相互作用而形成的D．光是一种波，同时也是一种粒子，光子说并未否定电磁说，在光子能量ε＝hν中，频率ν仍表示的是波的特性CD[光是一种波，同时也是一种粒子，光具有波粒二象性，A错误；当光和物质作用时，是“一份一份”的，表现出粒子性，光的干涉、衍射又说明光是一种波，光既不同于宏观的粒子，也不同于宏观的波，B错误，C正确；光具有波粒二象性，光的波动性与粒子性不是独立的，由公式ε＝hν可以看出二者是有联系的．光的粒子性并没有否定光的波动性，D正确．]2．(多选)从光的波粒二象性出发，下列说法正确的是()A．光是高速运动的微观粒子，每个光子都具有波粒二象性B．光的频率越高，光子的能量越大C．在光的干涉中，暗条纹的地方是光子不会到达的地方D．在光的干涉中，亮条纹的地方是光子到达概率最大的地方BD[一个光子谈不上波动性，A错误；暗条纹是光子到达概率小的地方，C 错误；光的频率越高，光子的能量E＝hν越大，在光的干涉现象中，光子到达的概率大小决定光屏上出现明、暗条纹，故B、D选项正确．]。

第一章． 波动方程§1 方程的导出。

定解条件1．细杆（或弹簧）受某种外界原因而产生纵向振动，以u(x,t)表示静止时在x 点处的点在时刻t 离开原来位置的偏移，假设振动过程发生的张力服从虎克定律，试证明),(t x u 满足方程()⎪⎭⎫ ⎝⎛∂∂∂∂=⎪⎭⎫ ⎝⎛∂∂∂∂x u E x t u x t ρ 其中ρ为杆的密度，E 为杨氏模量。

证：在杆上任取一段，其中两端于静止时的坐标分别为 x 与+x x ∆。

现在计算这段杆在时刻t 的相对伸长。

在时刻t 这段杆两端的坐标分别为：),();,(t x x u x x t x u x ∆++∆++其相对伸长等于),()],([)],([t x x u x x t x u x t x x u x x x ∆+=∆∆-+-∆++∆+θ 令0→∆x ，取极限得在点x 的相对伸长为x u ),(t x 。

由虎克定律，张力),(t x T 等于),()(),(t x u x E t x T x =其中)(x E 是在点x 的杨氏模量。

设杆的横截面面积为),(x S 则作用在杆段),(x x x ∆+两端的力分别为x u x S x E )()(x u x x S x x E t x )()();,(∆+∆+).,(t x x ∆+于是得运动方程 tt u x x s x ⋅∆⋅)()(ρx ESu t x =),(x x x x x ESu x x |)(|)(-∆+∆+利用微分中值定理，消去x ∆，再令0→∆x 得tt u x s x )()(ρx∂∂=x ESu () 若=)(x s 常量，则得 22)(tu x ∂∂ρ=))((x u x E x ∂∂∂∂ 即得所证。

2．在杆纵向振动时，假设(1)端点固定，(2)端点自由，(3)端点固定在弹性支承上，试分别导出这三种情况下所对应的边界条件。

解：(1)杆的两端被固定在l x x ==,0两点则相应的边界条件为.0),(,0),0(==t l u t u(2)若l x =为自由端，则杆在l x =的张力xu x E t l T ∂∂=)(),(|l x =等于零，因此相应的边界条件为 xu ∂∂|l x ==0 同理，若0=x 为自由端，则相应的边界条件为 xu ∂∂∣00==x (3)若l x =端固定在弹性支承上，而弹性支承固定于某点，且该点离开原来位置的偏移由函数)(t v 给出，则在l x =端支承的伸长为)(),(t v t l u -。

数学物理方程讲义姜礼尚答案LtD数学物理方程讲义姜礼尚答案【篇一：数学分析学习方法档】>从数学分析开始讲起：数学分析是数学系最重要的一门课，经常一个点就会引申出今后的一门课，并且是今后数学系大局部课程的根底。

也是初学时比拟难的一门课，这里的难主要是对数学分析思想和方法的不适应，其实随着课程的深入会一点点容易起来。

当大四考研复习再看时会感觉轻松许多。

数学系的数学分析讲三个学期共计15学分270学时。

将?数学分析?中较难的一局部删去再加上常微分方程的一些最简单的内容就是中国非数学专业的?高等数学?，或者叫数学一的高数局部数学分析书：初学从中选一本教材，一本参考书就根本够了。

我强烈推荐11，推荐1，2，7，8。

另外建议看一下当不了教材的16，20。

中国人自己写的：1?数学分析?陈传璋，金福临，朱学炎，欧阳光中著〔新版作者顺序颠倒〕应该是来自辛钦的?数学分析简明教程?，是数学系用的时间最长，用的最多的书，大局部学校考研分析的指定教材。

我大一用第二版，现在出了第三版，但是里面仍有一些印刷错误，不过克可以一眼看出来。

网络上可以找到课后习题的参考答案，不过建议自己做。

不少经济类工科类学校也用这一本书。

里面个别地方讲的比拟难懂，而且比其他书少了一俩个知识点，比方好似没有讲斯托尔滋(stolz)定理，实数的定义也不清楚。

不过仍然不失为一本好书。

能广泛被使用一定有它自己的一些优势。

2?数学分析?华东师范大学数学系著师范类使用最多的书，课后习题编排的不错，也是考研用的比拟多的一本书。

课本最后讲了一些流形上的微积分。

虽然是师范类的书，难度比上一本有一些降低，不过还是值得一看的。

3?数学分析?陈纪修等著以上三本是考研用的最多的三本书。

4?数学分析?李成章，黄玉民是南开大学一个系列里的数学分析分册，这套教材里的各本都经常被用到，总体还是不错的，是为教学改革后课时数减少后的数学系各门课编写的教材。

5?数学分析讲义?刘玉链我的数学分析老师推荐的一本书，不过我没有看，最近应该出了新版，貌似是第五？版，最初是一本函授教材，写的应该比拟详细易懂。

第四章 二阶线性偏微分方程的分类与总结§1 二阶方程的分类1． 证明两个自变量的二阶线性方程经过可逆变换后它的类型不会改变，也就是说，经可逆变换后2211212a a a -=∆的符号不变。

证：因两个自变量的二阶线性方程一般形式为fcu u b u b u a u a u a y x yy xy xx =+++++212212112经可逆变换 ⎩⎨⎧==),(),(y x y x ηηξξ 0),(),(≠y x D D ηξ化为 f u c u b u a u a u a =++++ηηηξηξξ22212112其中 ⎪⎪⎩⎪⎪⎨⎧++=+++=++=22212211222212111222212211112)(2y y x x y y x y y x x x y y x x a a a a a a a a a a a a ηηηηηξηξηξηξξξξξ所以 y x y x y x y x x y yx a a a aa a aηηξξηηξξηξηξ2211112222122221112222)(+-+=-=∆22221112222222211),(),())(()(⎥⎦⎤⎢⎣⎡∆=--=+-y x D D a a aa a x y y x y x y x ηξηξηξηξξη因0),(),(2>⎥⎦⎤⎢⎣⎡y x D D ηξ，故∆与∆同号，即类型不变。

2． 判定下述方程的类型（1）022=-yy xx u y u x （2）0)(2=++yy xx u y x u （3）0=+yyxx xyuu（4）)010001(sgn 0sgn 2sgn ⎪⎩⎪⎨⎧<-=>==++x x x x xuu yu yyxy xx(5) 0424=+++-zz yy xz xy xx u u u u u 解：(1)022=-yy xx u y u x因 022>=∆y x 当0,0≠≠y x 时0,0=>∆x 或0=y 时0=∆。

第一章． 波动方程§1 方程的导出。

定解条件1．细杆（或弹簧）受某种外界原因而产生纵向振动，以u(x,t)表示静止时在x 点处的点在时刻t 离开原来位置的偏移，假设振动过程发生的张力服从虎克定律，试证明),(t x u 满足方程()⎪⎭⎫⎝⎛∂∂∂∂=⎪⎭⎫ ⎝⎛∂∂∂∂x u E x t u x t ρ其中ρ为杆的密度，E 为杨氏模量。

证：在杆上任取一段，其中两端于静止时的坐标分别为 x 与+x x ∆。

现在计算这段杆在时刻t 的相对伸长。

在时刻t 这段杆两端的坐标分别为：),();,(t x x u x x t x u x ∆++∆++其相对伸长等于 ),()],([)],([t x x u xxt x u x t x x u x x x ∆+=∆∆-+-∆++∆+θ令0→∆x ，取极限得在点x 的相对伸长为x u ),(t x 。

由虎克定律，张力),(t x T 等于),()(),(t x u x E t x T x =其中)(x E 是在点x 的杨氏模量。

设杆的横截面面积为),(x S 则作用在杆段),(x x x ∆+两端的力分别为x u x S x E )()(x u x x S x x E t x )()();,(∆+∆+).,(t x x ∆+于是得运动方程tt u x x s x ⋅∆⋅)()(ρx ESu t x =),(x x x x x ESu x x |)(|)(-∆+∆+利用微分中值定理，消去x ∆，再令0→∆x 得tt u x s x )()(ρx∂∂=x ESu () 若=)(x s 常量，则得22)(tu x ∂∂ρ=))((x u x E x ∂∂∂∂即得所证。

2．在杆纵向振动时，假设(1)端点固定，(2)端点自由，(3)端点固定在弹性支承上，试分别导出这三种情况下所对应的边界条件。

解：(1)杆的两端被固定在l x x ==,0两点则相应的边界条件为 .0),(,0),0(==t l u t u(2)若l x =为自由端，则杆在l x =的张力x ux E t l T ∂∂=)(),(|lx =等于零，因此相应的边界条件为x u∂∂|lx ==0 同理，若0=x 为自由端，则相应的边界条件为xu∂∂∣00==x (3)若l x =端固定在弹性支承上，而弹性支承固定于某点，且该点离开原来位置的偏移由函数)(t v 给出，则在l x =端支承的伸长为)(),(t v t l u -。