斜拉桥的合理成桥状态
- 格式:doc
- 大小:27.00 KB
- 文档页数:3
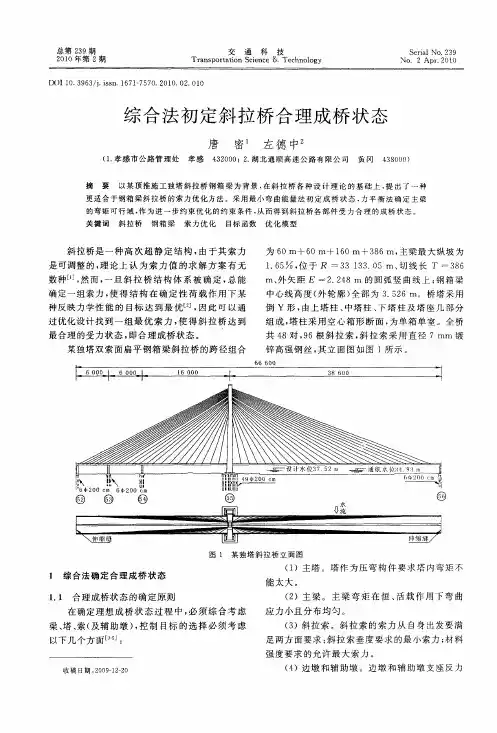


斜拉桥的设计过程与一般梁式桥的设计过程有所不同。
对于梁式桥梁结构,如果结构尺寸、材料、二期恒载都确定之后,结构的恒载内力也随之基本确定,无法进行较大的调整。
对于斜拉桥,由于其荷载是由主梁、桥塔和斜拉索分担的,合理地确定各构件分担的比例是十分重要的。
因此斜拉桥的设计首先是确定其合理的成桥状态,即合理的线形和内力状态,其中起主要调整作用的就是斜拉索的张拉力。
确定斜拉索张拉力的方法主要有刚性支承连续梁法、零位移法、倒拆和正装法、无应力状态控制法、内力平衡法和影响矩阵法等,各种方法的原理和适用对象请参考刘士林等编著的公路桥梁设计丛书—《斜拉桥》。
MIDAS/Civil 程序针对斜拉桥的张拉力确定、施工阶段分析、非线性分析等提供了多种解决方案,下面就一些功能的目的、适用对象和注意事项做一些说明。
1 .未闭合力功能通常,在进行斜拉桥分析时,第一步是进行成桥状态分析,即建立成桥模型,考虑结构自重、二期恒载、斜拉索的初拉力(单位力),进行静力线性分析后,利用未知荷载系数’的功能,根据影响矩阵求出满足所设定的约束条件(线形和内力状态)的初拉力系数。
此时斜拉索需采用桁架单元来模拟,这是因为斜拉桥在成桥状态时拉索的非线性效应可以看作不是很大,而且影响矩阵法的适用前提是荷载效应的线性叠加(荷载组合)成立。
第二步是利用算得的成桥状态的初拉力(不再是单位力),建立成桥模型并定义倒拆施工阶段,以求出在各施工阶段需要张拉的索力。
此时斜拉索采用只受拉索单元来模拟,在施工阶段分析控制对话框中选择体内力”第三步是根据倒拆分析得到的各施工阶段拉索的内力,将其按初拉力输入建立正装施工阶段的模型并进行分析。
此时斜拉索仍需采用只受拉索单元来模拟,但在施工阶段分析控制对话框中选择体外力”但是设计人员会发现上述过程中,倒拆分析和正装分析的最终阶段(成桥状态)的结果是不闭合的。
这是因为合拢段在倒拆分析和正装分析时的结构体系差异,导致正装分析时得到的最终阶段(成桥阶段)的内力与单独做成桥阶段分析(平衡状态分析)的结果有差异。



斜拉桥的合理成桥状态
斜拉桥是一种以斜拉索支撑主梁的桥梁结构,其合理成桥状态是指在斜拉桥建成后,其结构应该达到的一种理想状态,以保证桥梁的安全、稳定和经济运行。
斜拉桥的合理成桥状态包括以下几个方面:
1. 结构稳定:斜拉桥的结构应该具有足够的稳定性,能够承受各种荷载和风载的作用,同时在地震等自然灾害下也能够保持稳定。
2. 安全可靠:斜拉桥的结构应该具有足够的安全性和可靠性,能够保证车辆和行人的安全通行,同时在发生事故时也能够保证救援和维修的便利性。
3. 经济性好:斜拉桥的结构应该具有良好的经济性,能够在设计、施工和运营过程中尽可能地减少成本和资源的浪费,同时能够实现长期的经济效益。
4. 美观性好:斜拉桥的结构应该具有良好的美观性,能够与周围环境相协调,同时能够体现出设计者的创意和技术水平。
为了达到斜拉桥的合理成桥状态,需要在设计、施工和运营过程中进行全面的考虑和规划,同时需要进行严格的质量控制和监测,确保斜拉桥的安全、稳定和经济运行。




独塔不对称斜拉桥合理成桥状态分析付昌昌;蔡金标【摘要】以南台头闸大桥为工程背景,进行合理成桥状态的建模计算与分析.建立内力与线形双控制的索力优化模型,提出分步迭代的成桥思路,精确得到合理成桥状态.分析迭代塔、梁内力与线形、斜拉索索力的误差变化,研究成果对于独塔不对称斜拉桥合理成桥状态的确定具有参考意义.【期刊名称】《低温建筑技术》【年(卷),期】2019(041)006【总页数】5页(P117-120,126)【关键词】优化模型;迭代计算;合理成桥;线形控制【作者】付昌昌;蔡金标【作者单位】浙江大学建筑工程学院,杭州310058;浙江大学建筑工程学院,杭州310058【正文语种】中文【中图分类】TU3780 引言斜拉桥的合理成桥状态是指在确定荷载作用下,总能找到一组索力,使得各斜拉索力均匀,塔梁内力分布合理,成桥阶段满足变形、应力的要求[1]。
变截面不对称斜拉桥受力复杂,索塔承受竖向荷载以及因边主跨斜拉索不平衡力所产生的内力;主梁既承受斜拉索支承反力,又承受斜拉索所产生的不平衡轴压力,若采用单一的弯曲能量法确定合理成桥[2],其结果往往难以满足要求,因此,找寻合理成桥状态至关重要。
康晋[3]采用应力平衡法调整索力时,过程繁琐,优化标准不统一;Wu等[4]采用零位移法确定索力估算值,作为可行域的初始索力进行索力优化时,思路清晰,但误差较大,难以使内力与索力均合理。
1 研究思路首先按能量法初步确定初始索力,建立迭代优化模型,选取迭代控制参数,以塔梁受力合理,索力分布均匀、差异小为原则进行迭代计算;建立迭代终止条件,并得到恒载作用下的合理成桥状态。
最后还对迭代误差及迭代收敛性进行精确分析,见图1。
2 能量法迭代优化理论能量控制推导结果是一种线形控制[5],在由能量控制所确定成桥状态后,从内力角度对成桥状态进行优化补充,可实现成桥状态的双控。
图1 文中研究思路当需要对n个关心截面的内力状态进行控制时,这是一个约束条件为线性函数的优化问题,可通过线性规划法求解。
东北大学继续教育学院桥梁工程_试卷(作业考核线下)B 卷(共 4 页)1. 桥梁可变作用:指在结构使用期间,其量值随时间变化,且其变化值与平均值相比不可忽略的作用2. 预拱度:通过施工时预设的反向挠度来抵消永久作用挠度,使竣工后的桥梁达到理想的线型。
3. 合理拱轴线:当拱圈所选择的拱轴线与压力线相吻合时,这样的拱轴线称为合理拱轴线。
4. 斜拉桥合理成桥状态:一旦斜拉桥结构体系确定,总能找出一组斜拉索索力,使结构体系在确定荷载作用下,某种反应成桥受力状态的目标达到最优,这就是该目标下的合理成桥状态。
5. 圬工结构:圬工结构是指以砖、石材作为建筑材料,通过将其与砂浆或小石子混凝土砌筑而成的砌体所建成的结构为“砖石结构”;用砂浆砌筑混凝土预制块、整体浇注的混凝土或片石混凝土等构成的结构,成为“混凝土结构”通常我们把以上两种结构统称为“圬工结构”二、选择题(20分)1. 桥梁基本组成部分不包括( B )。
A. 上部结构;B. 路堤;C. 支座;D. 附属设施2. 对于简支梁桥,其净跨径、标准跨径、计算跨径之间的关系是( B )。
A. 净跨径<标准跨径<计算跨径;B. 净跨径<计算跨径<标准跨径;C. 计算跨径<标准跨径<净跨径;D. 标准跨径<净跨径<计算跨径3. 车道荷载用于桥梁结构的( )计算,车辆荷载用于桥梁结构的( C )计算。
A. 上部结构,下部结构;B. 局部加载,整体;C. 整体,局部加载、涵洞、桥台和挡土墙土压力等;D. 上部结构,整体4 对于跨河桥而言,流水压力属于( C )。
A. 永久作用;B. 基本可变作用;C. 其它可变作用;D. 偶然作用5. 在装配式预应力混凝土简支T形梁跨中部分采用下马蹄形截面的目的是( A )。
A. 便于布置预应力筋;B. 增强梁的稳定性;C. 承受梁跨中较大的正弯矩;D. 增强构件美观6. 装配式混凝土板桥的块件之间设置横向连接,其目的是( C )。
桥梁工程模拟3一、名词解释(25分):1.桥梁建筑高度:上部结构底缘至桥面顶面的垂直距离。
2.荷载横向分布系数:表示某根主梁所承担的最大荷载是各个轴重的倍数。
3. 承载能力极限状态设计:承载能力极限状态设计着重体现桥涵结构的安全性,是以塑性理论为基础,有两种作用效应组合,即基本组合和偶然组合。
4. 桥台:桥台一般设置在桥梁的两端,除了支承桥跨结构外,它又是衔接两岸接线路堤的构筑物,挡土护岸,承受台背填土及填土上车辆荷载所产生的附加侧压力。
5. 斜拉桥合理成桥状态:指斜拉桥在施工完成后,在所有恒载作用下,各构件受力满足某种理想状态,如梁、塔弯曲应变能最小。
二、选择题(20分):1. 对于行车道板厚度应不小于10cm的要求是为了(D )。
A. 方便模板的制作;B. 方便钢筋的布置;C. 保证板的刚度;D. 保证混凝土的浇筑质量2. 整体式板桥一般做成( A )截面。
A. 实体式等厚度的矩形;B. 实体式变厚度的矩形;C. 空心式等厚度的矩形;D. 空心式变厚度的矩形3. 整体式钢筋混凝土板桥承重板的计算单元是(B )。
A. 整体承重板;B. 1m宽板带;C. 荷载有效分布宽度的板;D. 行车道宽度的板4. 梁式桥与同样跨径的其它结构体系相比,梁桥内产生的( B )最大。
A. 剪力;B. 弯矩;C. 扭矩;D. 支座反力5. 拱不同于梁和柱的地方是它在竖向荷载作用下具有(D )。
A. 弯矩;B. 剪力;C. 轴向压力;D. 水平推力6. 下面几种桥型中只有(A )才属于圬工拱桥。
A. 双曲拱桥;B. 箱型拱桥;C. 桁架拱桥;D. 刚架拱桥7. 在地基比较差的地区修建拱桥时,最好修建(D )。
A. 空腹式拱;B. 无铰拱;C. 两铰拱;D. 三铰拱8. 装配式混凝土板桥的块件之间设置横向连接,其目的是(C )。
A. 减少车辆震动;B. 增加行车道的美观;C. 增强板桥的整体性;D. 避免块件之间横桥方向的水平位移9. 实腹式拱桥,若不计弹性压缩的影响,拱轴线与结构重力压力线相重合,此时拱圈在结构重力作用下各个截面(D )。
斜拉桥施工状态的确定方法一、概述通常,斜拉桥要实现最终的成桥状态豁要经过一系列的施工步骤。
根据主梁的施工方法不同有支架现浇法、支架拼装法、顶推法、悬臂现浇法、悬臂拼装法。
从斜拉索的张拉次数不同可分为一次张拉法和多次张拉法。
从悬僻现浇挂篮的支承方式不同可分为后支点挂篮和前支点挂篮。
支架现浇法或支架拼装法的主梁是在支架上进行现浇或拼装的,一般为落地支架。
通常用于规模较小的斜拉桥。
顶推法是指主梁采用顶推法施工的情况,一般也只适用于较小规模的斜拉桥。
悬臂现浇法是利用挂篮进行主梁的施工,通常相应梁段的斜拉索必须同步施工,对于采用后支点挂篮施工的情况,一个标准梁段的施工工序通常为:①挂篮前移并立模定位;②安装钢筋等、浇注混凝土;③混凝土待强后,张拉梁内预应力;④挂对应梁段的斜拉索并进行张拉。
对于采用前支点挂篮施工的情况,一个标准梁段的施工工序通常为:①挂篮前移并立模定位;②挂当前梁段斜拉索与挂篮前端相连并进行第一次张拉;③安装钢筋等、浇注部分混凝土;④当前梁段斜拉索进行第二次张拉;⑤浇完梁段混凝土;⑥混凝土待强后张拉梁内预应力;⑦降挂篮,当前梁段斜拉索进行第三次张拉。
悬臂拼装法是利用浮吊或桥面吊机将预制好的梁段逐段拼装的,通常斜拉索也必须同步安装并张拉。
悬臂施工法(现浇或拼装)施工达到最大悬臂后,要进行合龙段施工,如标准的三跨双塔斜拉桥,一般分别以两个主塔为中心进行双悬臂施工,达到最大悬臂后先合龙边跨,然后再进行中跨合龙施工,各跨的合龙施工是斜拉桥施工中极其关键的环节,通常的合龙程序为:①安装合龙段混凝土施工的吊架;②配平衡重施加在合龙口两侧;③利用定位装置嵌定合龙口;④安装钢筋等、浇注合龙段混凝土并逐级去掉合龙口两侧的平衡重;⑤张拉合龙预应力束。
如果平衡重与合龙梁段的重盆相等,则合龙口嵌定装置基本上不承受由合龙段混凝土浇注引起的内力。
合龙程序还有一个核心问题就是平衡重施加的时间。
这里是在合龙口嵌定之前,施加在主梁最大悬臂状态下,如果在合龙门嵌定之后施加,则由于嵌定装置使主梁成为了连续结构,其受力情况完全不一样,并且,合龙口嵌定装置需承受由平衡重引起的很大的内力,对成桥状态的主梁弯矩影响很大,后者与前者相比,跨中区域产生较大的恒载正弯矩,与该区域的控制弯矩同号,是不利的。
斜拉桥的合理成桥状态
一、概述
在通常意义下,桥梁的设计必须遵照适用、经济、安全和美观的基本原则,这在桥梁的初步设计阶段显得尤为突出。
桥梁初步设计要解决桥型方案问题,即根据行车、通航等使用要求,选定合适的桥梁类型和立面布置,确定主要的结构尺寸。
对于斜拉桥方案,需确定塔的个数、主跨大小、边跨与主跨比例、主梁的截面形式和高度、主塔的形式、斜拉索的布置、主梁与塔和墩的连接或支承方式等主要参数。
这些主要参数的确定通常是先根据经验初拟。
进行结构分析计算出设计内力,进行截面设计确定配筋和验算应力或裂纹,如果内力和截面设计结果不合理。
再修正有关参数重新作结构分析和截面设计,直至满足规范要求。
传统的设计方法在计算设计内力时,通常采用一次落架法计算恒载内力,这对于结构体系比牧简单的桥梁(如简支梁桥,采用一次落架法施工的中小型桥梁)来说是可行的,但对于斜拉桥,由于斜拉索需要进行预张拉,因此即使采用一次落架法施工,结构内力的计算也不是确定的。
斜拉桥一般采用悬臂法施工,最终的成桥恒载受力状态是通过施工过程一步步形成的,施工过程中斜拉索要逐根安装并进行张拉。
施工工序和张拉索力决定了桥梁在施工过程中的受力,也决定了成桥的恒载受力状态。
但张拉索力的确定又必须有一个已知的成桥恒载受力状态作为目标才能实现。
因此斜拉桥的设计计算首先要解决成桥受力状态的问题。
前,桥梁的设计规范采用极限状态理论,分正常使用和承载能力两种极限状态。
按正常使用极限状态验算结构刚度、截面应力或裂纹宽度:按承载能力极限状态验算截面的极限抗力。
通常按弹性理论进行结构内力计算,按此内力进行验算。
但由于斜拉桥为高次超静定结构,如果要分析结构的极限承载力,则必须考虑材料的塑性,充分计入材料和儿何非线性引起的结构内力重分布,才能真正求出结构的极限承载力,国内外在这方面有一些研究,但还有不少问题需要解决。
二、斜拉桥成桥受力状态确定方法
斜拉桥成桥受力状态包括成桥恒载内力状态和主梁线形状态,并且对于混凝土斜拉桥,由于混凝土收缩徐变的影响,成桥后相当一段时间内恒载内力状态和主梁线形状态会随时间变化,通常认为5年后才能基本稳定。
成桥恒载状态应以混凝土收缩徐变荃本完成后的稳定状态为准,但在变化阶段桥梁也应能满足使用要求。
主梁线形状态主要指成桥恒载状态下主梁的标高符合设计标高的要求。
这通常在初步设计阶段根据使用要求确定了桥下通航净空、桥面纵坡、竖曲线后就成为了一个明确的目标。
为了考虑活载的影响,通常还设里一定的预拱度。
成桥恒载内力状态可以按一次成桥(形成桥粱最终结构)的方法来确定,特别是在初步设计阶段,可以暂不考虑具体的节段施工过程,只针对于最终的成桥状态来确定其内力状态。
这实际上也是定出一个成桥的受力目标。
斜拉桥的成桥状态确定是设计中要解决的一个结构受力问题。
现代斜拉桥从1955年瑞典修建的主跨182。
6米的Stromsund钢斜拉桥以来还只有40多年的历史,早期的斜拉桥以稀索体系为特征,如1962年委内瑞拉的主跨235米的Maracaibo桥,每个塔上只有一对索,由于索的数量少,成桥方法也较简单,容易用试算的办法人工调整索力来满足结构的受力要求。
1967年德国波恩建成的Friedrich—Ebert桥,跨径280米,该桥采用了密索体系,它可以使索的锚固力减小,主梁受力均匀,易于悬臂施工,这个设计构思为以后的斜拉桥作出了典范,今天的斜拉桥几乎都是密索体系,主梁截面轻型,以受压为主。
密索体系使斜拉桥成为了高次超静定,主梁受力对索力大小很敏感,为了寻求合理的成桥受力状态,各种方法应运而生,主要方法有:刚性支承连续梁法;零位移法;内力平衡法;指定应力法;弯曲能量最小法;弯矩最小法;用索量最小法和影响矩阵法。
1)刚性支承连续梁法。
该法是使用最早的方法之一,其原理是,把斜拉索提供的弹性竖向支承视为刚性的竖向支承,按普通连续梁求出这些刚性支承的反力,以此作为斜拉索索力的竖向分力。
这种方法确定的索力可能导致索力跳跃很大,不均匀,但主梁有矩很小。
对于不对称结构塔的有矩难以照顾,所得结果将难以应用。
2)零位移法。
该法是通过合理选择索力使成桥状态结构在恒载作用下,索梁交点处位移为零。
这种方法由于受力原理与刚性支承连续梁法类似,因此,结果也很一致,而此法由于计入了索的水平分力影响,更为合理些。
此法同样有对于不对称结构,塔的有矩难以照顾的问题。
3)内力平衡法。
该法是以控制截面内力为目标,通过合理选择索力,来实现这一目标,控制截面可包括主梁和塔,因此,主梁和塔的内力都可照顾到,如控制截面及相应的控制值选择合理,效果会比前两种方法好,但同样有索力可能不均匀的问题。
4)指定应力法。
该法是以控制截面的应力为目标,方法和效果与内力平衡法类似。
5)弯曲能量最小法。
该法是以结构(包括梁、塔、墩)弯曲应变能作为目标函数,如果不加任何约束条件(即无约束优化问题),则该法在应用时,可转变为作一次结构分析的问题,其中只要让梁、塔、索的轴向刚度取大数,梁和塔的弯曲刚度不变,把全部恒载加在结构上,所得的内力状态即为所求。
这样求出的结果一般弯矩均比较小,但两端的索力不均
匀,如人为作索力的局部调整,容易将受力状态调乱,较难得到索力和梁塔内力均满意的结果。
另外,由于未考虑活载的影响,因此,恒载弯矩小并非都合理。
6)弯矩最小法。
该法是以结构(包括梁、塔、墩)弯矩平方和作为目标函数,其结果与弯曲能量最小法接近。
7)用索量最小法侧。
该法是以索力乘索长的累计值作为目标函数,一般要加约束条件,如索力均匀性约束,控制截面内力约束,用这种方法时,约束条件的选取至关,要,选取不合理,则难以获得理想结果。
由于实际的成桥状态是由施工过程一步步生成的,并且成桥后的前几年桥梁的内力和主梁线形还因混凝土收缩徐变的影响而变化,因此,这样确定的成桥主梁线形状态和恒载内力状态只能作为一个目标值,为下一步确定施工状态明确一个成桥目标。