当前位置：文档之家 › 物化03_第一定律,功,可逆过程

物化03_第一定律,功,可逆过程

  • 格式：ppt
  • 大小：182.50 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

物化 热力学第一定律

物化 热力学第一定律

p 'V '
p2
V1
V'
p2V2
V2
V
可见，外压差距越小，膨胀次数越多，做的 功也越多。
（4）外压比内压小一个无穷小的值 外压相当于一杯水，水不断蒸发，这样的膨胀 过程是无限缓慢的，每一步都接近于平衡态。 所作的功为：
We,4 pe dV ( pi dp)dV
p
p1
p1V1
习题2： 设有一装臵（如图），（1）将隔板抽去以后， 以空气为系统时，ΔU、Q、W为正为负还是 零？（2）如右方小室也有空气，不过压力比 左方小，将隔板抽去以后，以所有空气为系统 时，ΔU、Q、W为正为负还是零？
习题3： （1）如果一系统从环境接受了160J功，热力学 能增加了200J，问系统将吸收或放出多少热？ （2）一系统在膨胀过程中对环境做了10540J 的功，同时吸收了27110J的热，问系统的热 力学能变化若干？
p1V1
p 'V '
p2 V1
p2V2
V2 V
p2
V1
V'
p2V2 p 2
V2p2V2V1源自VV2 V功与变化的途径有关
总结，可逆过程的特点：
(1)推动力无限小，进行得无限慢，中间经历 一系列平衡态； (2)过程结束后，系统若沿原途径逆向进行恢 复到始态，则环境也同时复原。 (3) 可逆过程系统对环境作最大功（环境对系 统作最小功）。
习题5： 在一礼堂中有950人在开会，每个人平均每小 时向周围散发出1.2×105J的热量，如果以 除了人以外的其它一切为系统，则在开会 时的开始20分钟内系统热力学能增加了多 少？如果以礼堂中的一切（包括人）为系 统，则系统的ΔU为多少？

《化学热力学》物化第一章

《化学热力学》物化第一章
其中可逆膨胀系统对环境作功最大可逆压缩环境对系统作功最小其中可逆膨胀系统对环境作功最大可逆压缩环境对系统作功最小w可逆膨胀可逆膨胀ww可逆压缩可逆压缩在过程进行的每一瞬间系统都接近于平衡状态以致在任意选取的短时间dt内整个过程可以看成是由一系列极接近平衡的状态所构成这种过程称为准静态过程
第一章
热力第学一第一章定律 热力学第一定律
1. 系统为电炉丝，其状态未变，故ΔU=0，水(环境)吸热Q<0 ，电源(环境)做功W>0
2. 系统为电炉丝和水，是绝热系统，故Q=0，电源(环境) 做功W>0，ΔU=Q+W= W> 0
3. 电炉丝、电源和水为系统时，是孤立系统，故ΔU=0， Q=0，W=0
§1.4 体积功
1.体积功 2.可逆过程 3.相变体积功
§1.1 热力学概论
1.热力学的研究对象 (1)变化过程中的能量转换的定量关系 ——热力学第一定律 (2)变化过程的方向和限度 ——热力学第二定律
(3)规定熵——热力学第三定律， ——解决熵的计算问题。
热力学基本原理在化学中的应用——化学热力学 。 化学热力学主要研究和解决的问题：
(1)研究化学过程及该过程中的能量效应； (2)判断化学过程在一定条件下是否可能进行， 该过程的方向和所能取得的产物的最大（小） 产量。
经典热力学主要研究封闭系统。
2. 状态和状态性质（状态函数）
状态：系统的物理性质和化学性质的综合表现。 状态性质：系统处于某一状态时的性质，就是一些
系统本身所属的宏观物理量。
T，p, ，V，m， U，H，S…
常见的状态函数
状态性质之间互相联系的，不是独立的，在数学 上有函数关系，所以又称状态函数。
48
44

物化各种公式概念总结

物化各种公式概念总结

第一章热力学第一定律一、基本概念系统与环境，状态与状态函数，广度性质与强度性质，过程与途径，热与功，内能与焓。

二、基本定律 热力学第一定律：ΔU =Q +W 。

三、基本关系式1、体积功的计算 δW = －p 外d V恒外压过程：W = －p 外ΔV定温可逆过程（理想气体）：W =nRT 1221ln ln p p nRT V V = 2、热效应、焓：等容热：Q V =ΔU （封闭系统不作其他功）等压热：Q p =ΔH （封闭系统不作其他功）焓的定义：H =U +pV ; ΔH =ΔU +Δ(pV )焓与温度的关系：ΔH =⎰21d p T T T C3、等压热容与等容热容：热容定义：V V )(T U C ∂∂=；p p )(T H C ∂∂= 定压热容与定容热容的关系：nR C C =-V p热容与温度的关系：C p ，m =a +bT +cT 2四、第一定律的应用1、理想气体状态变化等温过程：ΔU =0 ; ΔH =0 ; W =－Q =⎰-p 外d V等容过程：W =0 ; Q =ΔU =⎰T C d V ; ΔH =⎰T C d p等压过程：W =－p e ΔV ; Q =ΔH =⎰T C d p ; ΔU =⎰T C d V可逆绝热过程：Q =0 ; 利用p 1V 1γ=p 2V 2γ求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d pC V (㏑T 2-㏑T 1)=nR(㏑V 1-㏑V 2)（T 与V 的关系）C p (㏑T 2-㏑T 1)=nR(㏑P 2-㏑P 1) (T 与P 的关系)不可逆绝热过程：Q =0 ;利用C V (T 2-T 1)=－p 外(V 2-V 1)求出T 2,W =ΔU =⎰T C d V ;ΔH =⎰T C d p2、相变化 可逆相变化：ΔH =Q =n ΔH ； Ｗ＝－p (V 2-V 1)=－pV g =－nRT ; ΔU =Q +W3、实际气体节流膨胀：焦耳-汤姆逊系数：μJ-T （理想气体在定焓过程中温度不变，故其值为0；其为正值，则随p 降低气体T 降低；反之亦然）4、热化学标准摩尔生成焓：在标准压力和指定温度下，由最稳定的单质生成单位物质的量某物质的定压反应热（各种稳定单质在任意温度下的生成焓值为0） 标准摩尔燃烧焓：…………，单位物质的量的某物质被氧完全氧化时的反应焓第二章 热力学第二定律一、基本概念 自发过程与非自发过程二、热力学第二定律热力学第二定律的数学表达式（克劳修斯不等式）T Q dS δ≥ “=”可逆；“＞”不可逆三、熵（0k 时任何纯物质的完美结晶丧子为0）1、熵的导出：卡若循环与卡诺定理（页522、熵的定义：T Q dS r δ=3、熵的物理意义：系统混乱度的量度。

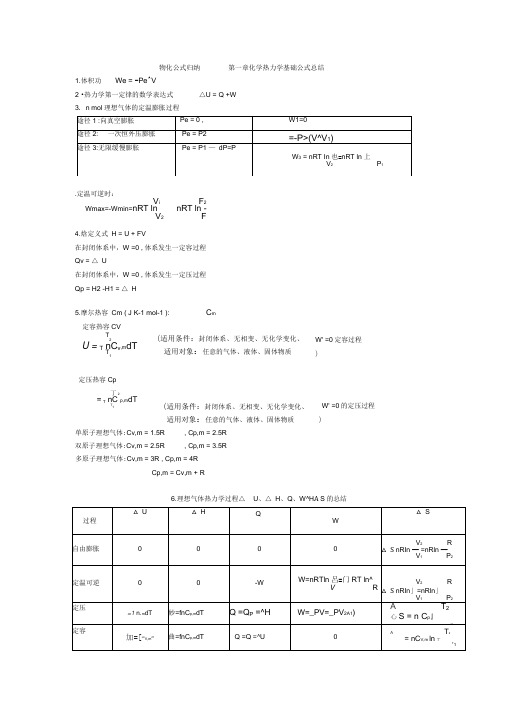
物化公式归纳

物化公式归纳

物化公式归纳 第一章化学热力学基础公式总结1.体积功 We = -Pe ^V2 •热力学第一定律的数学表达式△U = Q +W 3. n mol 理想气体的定温膨胀过程 .定温可逆时： V iF 2Wmax=-Wmin=nRT ln nRT ln -V 2F4.焓定义式 H = U + FV 在封闭体系中，W =0 ,体系发生一定容过程 Qv = △ U 在封闭体系中，W =0 ,体系发生一定压过程 Qp = H2 -H1 = △ H5.摩尔热容 Cm ( J K-1 mol-1 ):C m 定容热容CV T2 U = T nC v ,m dTT 1(适用条件：封闭体系、无相变、无化学变化、适用对象：任意的气体、液体、固体物质 W' =0定容过程 )定压热容Cp 丁2= T nC p,m dT T1(适用条件：封闭体系、无相变、无化学变化、W' =0的定压过程适用对象：任意的气体、液体、固体物质 ) 单原子理想气体:Cv,m = 1.5R , Cp,m = 2.5R 双原子理想气体:Cv,m = 2.5R, Cp,m = 3.5R 多原子理想气体:Cv,m = 3R , Cp,m = 4R Cp,m = Cv,m + R6.理想气体热力学过程△ U 、△ H 、Q 、W^H A S 的总结C p dT△ Cp ( T2 - T1)10.热机的效率为 对于卡诺热机 W Q 亠 Q 2Q 2--- zzj -------------- =1 "r ： Q Q [ ---------------- Q [W Q 1 Q Q 1Q|★ ~T 2 T 1可逆循环过程不可逆循环过程11.熵变定义式 (体系经历一可逆过程的热温商之和等于该过程的熵变.)7. 定义：△ fHm 9 (kJ mol-1)-- 标准摩尔生成焓 △ H —焓变；△ rHm —反应的摩尔焓变 △ rHm 9 — 298K 时反应的标准摩尔焓变；△ fHm 9 (B) — 298K 时物质B 的标准摩尔生成焓； △ cHm 9 (B) — 298K 时物质B 的标准摩尔燃烧焓。

物化——热力学四大定律发现者

物化——热力学四大定律发现者

• 热力学的四大定律简述如下： 热力学的四大定律简述如下： 四大定律简述如下 热力学第零定律——如果两个热力学系统 热力学第零定律 如果两个热力学系统 中的每一个都与第三个热力学系统处于热 平衡(温度相同 温度相同)， 平衡 温度相同 ，则它们彼此也必定处于热 平衡。 平衡。 热力学第一定律——能量守恒定律在热学 能量守恒定律在热学 热力学第一定律 形式的表现。 形式的表现。 热力学第二定律——力学能可全部转换成 力学能可全部转换成 热力学第二定律 热能， 热能， 但是热能却不能以有限次的实验操 热机不可得)。 作全部转换成功 (热机不可得 。 热机不可得 热力学第三定律——绝对零度不可达到但 热力学第三定律 绝对零度不可达到但 可以无限趋近
卡诺循环工作原理图
• 卡诺指出了热机工作过程中最本质的东西： 卡诺指出了热机工作过程中最本质的东西： 热机必须工作于两个热源之间， 热机必须工作于两个热源之间，才能将高 温热源的热量不断地转化为有用的机械功； 温热源的热量不断地转化为有用的机械功； 明确了“ 明确了“热的动力与用来实现动力的介质 无关， 无关，动力的量仅由最终影响热素传递的 物体之间的温度来确定”，指明了循环工 物体之间的温度来确定” 作热机的效率有一极限值， 作热机的效率有一极限值，而按可逆卡诺 循环工作的热机所产生的效率最高。 循环工作的热机所产生的效率最高。实际 上卡诺的理论已经深含了热力学第二定律 的基本思想，但由于受到热质说的束缚， 的基本思想，但由于受到热质说的束缚， 使他当时未能完全探究到问题的底蕴。 使他当时未能完全探究到问题的底蕴。
• 卡诺出色地运用了理想模型的研究方 以他富于创造性的想象力， 法，以他富于创造性的想象力，精心 构思了理想化的热机——后称卡诺可 后称卡诺可 构思了理想化的热机 后称 逆热机（卡诺热机）， ），提出了作为热 逆热机（卡诺热机），提出了作为热 力学重要理论基础的卡诺循环和卡诺 定理， 定理，从理论上解决了提高热机效率 的根本途径

物化公式

物化公式

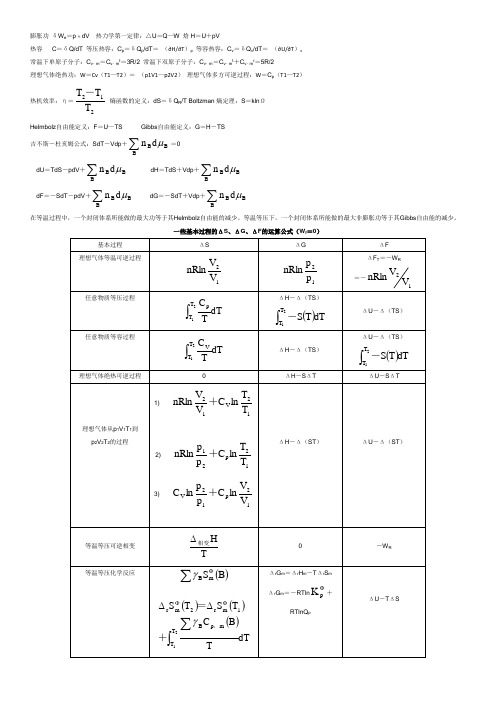
膨胀功 δW e ＝p 外dV 热力学第一定律：△U ＝Q —W 焓H ＝U ＋pV热容 C ＝δQ/dT 等压热容：C p ＝δQ p /dT ＝ （∂H/∂T ）p 等容热容：C v ＝δQ v /dT ＝ （∂U/∂T ）v 常温下单原子分子：C v ，m ＝C v ，m t ＝3R/2 常温下双原子分子：C v ，m ＝C v ，m t ＋C v ，m r ＝5R/2理想气体绝热功：W ＝Cv （T1—T2）＝ （p1V1—p2V2） 理想气体多方可逆过程：W ＝C p （T1—T2）热机效率：η＝212T T T － 熵函数的定义：dS ＝δQ R /T Boltzman 熵定理：S ＝kln ΩHelmbolz 自由能定义：F ＝U —TS Gibbs 自由能定义：G ＝H －TS 吉不斯－杜亥姆公式：SdT －Vdp ＋∑BBBd nμ＝0dU ＝TdS －pdV ＋∑B BBd nμ dH ＝TdS ＋Vdp ＋∑B BBd nμdF ＝－SdT －pdV ＋∑BBBd nμ dG ＝－SdT ＋Vdp ＋∑BBBd nμ在等温过程中，一个封闭体系所能做的最大功等于其Helmbolz 自由能的减少。

等温等压下，一个封闭体系所能做的最大非膨胀功等于其Gibbs 自由能的减少。

一些基本过程的ΔS 、ΔG 、ΔF 的运算公式（W f ＝0）基本过程ΔSΔGΔF 理想气体等温可逆过程12V V nRln12p p nRlnΔF T ＝－W R＝－12V V nRln任意物质等压过程dTTC 21T T p ⎰ΔH －Δ（TS ）()dTT S 21T T ⎰－ΔU －Δ（TS ）任意物质等容过程dTTC 21T T V ⎰ΔH －Δ（TS ）ΔU －Δ（TS ）()dTT S 21T T ⎰－理想气体绝热可逆过程ΔH －S ΔT ΔU －S ΔT理想气体从p 1V 1T 1到p 2V 2T 2的过程1)12V 12T T lnC V V nRln＋ 2)12p 21T T lnC p p nRln＋3)12p 12V V V lnC p p ln C ＋ΔH －Δ（ST ）ΔU －Δ（ST ）等温等压可逆相变TH 相变∆－W R等温等压化学反应()B S m B∑Φγ()()()dTTB C T S T S 21T T m p B 1mr 2mr ⎰∑ΦΦ∆∆，＋＝γΔr G m ＝Δr H m －T Δr S m Δr G m ＝－RTln Φp K ＋RTlnQ pΔU －T ΔS溶液组成的表示法：（1）物质的量分数：B B n x n＝（2）质量摩尔浓度：B B An m W ＝（3）物质的量浓度：B B n c V＝（4）质量浓度B ω拉乌尔定律A A A p p x *＝ 亨利定律：x m B c Bp k x k m k c ＝＝＝化学势的各种表示式和某些符号的物理意义： 气体：（1）纯理想气体的化学势()()T,p T RT ln ppμμΦΦ＝＋ 标准态：任意温度，p ＝p φ＝101325Pa 。

2017物理化学热力学第一章3


δQ＝0，dU＝δW
理想气体单纯p，V，T 变化 dU＝CV dT
所以
W
T2 T1
CV
dT
n
T2 T1
CV
,mdT
若视CV，m为常数
W＝n CV，m (T2－T1)
无论绝热过程是否可逆，上式均成立。
25
1.6 理想气体的绝热过程
2） 理想气体绝热可逆过程方程式
δQ＝0，若δW ′＝0 则 dU＝δW
解 上述过程为定压过程，定压下吸收的热为
Qp
(H ) p
n
T2 T1
C
p , m dT
查表可得CO2的Cp,m随温度的变化的经验公式为
C p,m


44.14

9.04
103

T K

8.54 105 (T / K)2

J

K
-1

mol-1

将此式代入上式可得
19
例题
Qp
H Qp CpdT (b)
式(a)及(b)对气体分别在等容、等压条件下单纯发生温度改变时计算U， H均适用。而对液体、固体不分定容、定压，单纯发生温度变化时均可近似 应用。
10
1.5 热容
CV 和Cp的关系（习题21）
对于纯物质单相密闭系统（双变量系统）：
d U U d T U d V
根据定义式 dH = dU + dpV
dH

C pdT


H p
T dp
dU

CV dT

U V
T
dV
C pdT

第一章：热力学第一定律(物理化学)


We,1 = -p1(V1- V2) =p1(V2 - V1)
功与过程
2.多次等外压压缩 第一步：用 p" 的压力将系统从 V2 压缩到V " ； 第二步：用 p ' 的压力将系统从V " 压缩到V ' ； 第三步：用 p1 的压力将系统从V ' 压缩到 V1 。 We = -p”(V”- V2) +[- p ’(V’ - V”)] + [-p1 (V”- V1)] 整个过程所作的功为三步加和。
系统吸热，Q>0； 功（work）
系统放热，Q<0 。
环境对系统作功，W >0； 系统对环境作功，W<0 。
1. 如图，在绝热盛水容器中，浸入电阻丝，通电一段 时间，通电后水及电阻丝的温度均略有升高，今以电阻 丝为系统------------------------------------- ( ) （A） W =0，Q <0， ΔU <0 （B）W >0， Q <0， ΔU >0 （C） W <0， Q <0， ΔU >0 （D） W >0， Q =0， ΔU >0 若以电阻丝，水以及绝热水槽为系统又如何？？
d(U pV )
H U pV
积分式
Qp DH
3.焓(enthalpy)
焓的定义式： 发生微变时：
H U pV
dH d(U pV ) dU pdV Vdp
系统由始态到末态的焓变
DH DU D( pV )
为什么要定义焓？ 为了使用方便，因为在等压、不作非膨胀功的条 Q p 容易测定，从而 Qp 件下，焓变等于等压热效应 。 可求其它热力学函数的变化值。 焓是状态函数 定义式中焓由状态函数组成。 焓不是能量 具有能量的单位，但不守恒。

物理化学 02章_热力学第一定律(三)



因为 所以
p1V1 p2V2 K
p2V2 p1V1 nR(T2 T1) W= 1 1
绝热功的求算 （2）绝热状态变化过程的功
W U CV dT
T1
T2
= CV (T2 T1)
(设CV 与T 无关）
因为计算过程中未引入其它限制条件，所以
该公式适用于定组成封闭系统的一般绝热过程， 不一定是可逆过程。
Th
D(p4 ,V4 , TC )
C (p3 ,V3 , TC )
环境对系统所作的功如
O
Tc
DA曲线下的面积所示。
a
d
b
c
V
Carnot 循环
过程4：绝热可逆压缩
p
A(p1 ,V1 , Th ) B(p2 ,V2 , Th )
D( p4 ,V4 , TC ) A( p1,V1, Th )
Th
D(p4 ,V4 , TC )
表示经节流过程后，气体温度随压 力的变化率。
J-T是系统的强度性质。因为节流过程的 dp 0 ,
所以当：
J-T >0 J-T <0 J-T =0
经节流膨胀后，气体温度降低。 经节流膨胀后，气体温度升高。 经节流膨胀后，气体温度不变。
转化温度（inversion temperature)
Qc ' Tc W Th Tc
式中W表示环境对系统所作的功。
热泵
热泵的工作原理与致冷机相仿。
把热量从低温物体传到高温物体，使高温物体
温度更高。
热泵的工作效率等于：向高温物体输送的热与
电动机所做的功的比值。
热泵与致冷机的工作物质是氨、溴化锂（氟

(2)-01章-热力学第一定律(可逆过程,体积功,焓,热容)

物理化学电子教案—第一章
热力学第一定律及其应用
环境 surroundings
无物质交换 封闭系统
Closed system
U Q W
有能量交换
上一内容 下一内容 回主目录
返回
2020/3/7
热力学第一定律
Joule（焦耳）和 Mayer（迈耶尔)自1840年 起，历经20多年，用各种实验求证热和功的转 换关系，得到的结果是一致的。
也可以表述为：第一类永动机是不可能制成的
第一类永动机（first kind of perpetual motion machine):一种既不靠 外界提供能量，本身也不减少能量，却可以不断对外作功的机器 称为第一类永动机，它显然与能量守恒定律矛盾。
热力学第一定律是人类经验的总结，事实证明违背该定 律的实验都将以失败告终，这足以证明该定律的正确性。
U U2 U1 QW 对于微小变化 dU Q W
热力学能的单位： J
热力学能是状态函数，用符号U表示，它的 绝对值尚无法测定，只能求出它的变化值。
上一内容 下一内容 回主目录
返回
2020/3/7
热力学第一定律的文字表述
热力学第一定律是能量守恒与转化定律在热现 象领域内所具有的特殊形式，说明热力学能、热和 功之间可以相互转化，但总的能量不变。
自然界的一切物质都具有能量，能量有各 种不同形式，能够从一种形式转化为另一种形 式，但在转化过程中，能量的总值不变。
上一内容 下一内容 回主目录
返回
2020/3/7
热力学能
系统总能量通常有三部分组成：
（1）系统整体运动的动能 （2）系统在外力场中的位能 （3）热力学能，也称为内能 热力学中一般只考虑静止的系统，无整体运动， 不考虑外力场的作用，所以只注意热力学能
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

δW = p外dV
W = ∫ p外dV
V1 V2
系统，V
（1）被积函数为p外（系统与环境的压力一直相等） （2）此式中的W与第一定律表达式中的W相同吗？
(3) 具体过程的体积功： 等压外过程： = p外∆V W 等压过程： W = p∆V
W = ∫ p外dV
V1 V2
自由膨胀： W = 0 等容过程： W = 0 理气等温可逆膨胀(压缩)： = nRT ln V2 W V1
(1) 适用于非敞开系统
Ⅰ
(2)
1 Ⅱ
2
∆U = Q − W = QⅡ − WⅡ Ⅰ Ⅰ
§2－3 功的计算 (How to calculate work)
一、功的分类 体积功 Volume work 功 非体积功 电功 表面功 光 轴功，等
二、体积功的计算
p外 dV
若体积膨胀或压缩dV (即V→V+dV)，则
= ∆ (U + pV ) + W '
Q p = ∆H + W '
Q p = ∆H
条件：等压
条件：等压，W’=0
三、热容和简单变温过程热的计算 简单变温过程： δQ 热容 (Heat capacity)： C = dT 1. 等容热容
∂U CV = ∂ T V
等容 dU = CV dT
可逆膨胀：理想活塞 p外＝p-dp
力学平衡
W = ∫ p外dV = ∫ ( p − dp )dV = ∫ pdV
Байду номын сангаасV1 V1 V1
V2
V2
V2
=∫
V2
V1
nRT V dV = nRT ln 2 V V1
等温膨胀 W＝？ H2(1000Pa, 3m3)
例：1mol H2 (3000Pa, 1m3)
(1) 若 p外＝0 (自由膨胀)：W＝0 (2) 若 p外＝1000 Pa (一次膨胀)：W＝1000×(3-1) J ＝2000 J (3) 可逆膨胀：
∆U = ∫ CV dT
T1 T2
∂U 令 U = U(T, V)，则 dU = CV dT + dV ∂V T
条件：等容简单变温过程
2. 等压热容
∂H Cp = ∂T p
令 H = H(T, p)，则 等压 dH = C p dT
∂H dH = C p dT + ∂p
QV = ∆U
条件：等容，W’＝0
二、等压热和焓 (Heat of isobaric process and enthalpy) 定义： H = U + pV H是状态函数，容量性质，J， H＝H(T, p)无物理意义
Q = ∆U + W
等压 Q p = ∆U + ( p∆V + W ' )
= ∆U + ∆ ( pV ) + W '
按过程本身的特点，分为多种多样。 物化感兴趣的几种典型过程为： 等温过程：T1＝T2＝T环＝const. 等压过程：p1＝p2＝p外＝const. 等容过程：V＝const. 绝热过程： 循环过程：
五、热量和功 (Heat and work) 定义：由于温度不同而在系统与环境 之间传递的能量，Q； 除热以外，在系统与环境之间 所传递的能量，W。 符号：系统吸热，Q > 0；系统放热，Q < 0 系统做功，W > 0；环境做功，W < 0 Q和W是过程量：
∆ H = ∫ C p dT
T1 T2
dp T
条件：等压简单变温过程 工程和实验过程中最常用！
特点： （1）相互关联：单组分均相封闭 系统有两个独立变量；（无组成 变化的封闭系统） （2）变化只决定于初末状态
∫c (A, B) d Y = ∫c (A, B) d Y
1 2
= YB − YA = ∆ Y
四、过程与途径 (Process and path) 按系统初末状态的差异，分为 简单物理过程：p V T 变化 复杂物理过程：相变、混合等 化学过程：
3. 几种典型可逆过程： （1）可逆膨胀和可逆压缩：力学平衡 （2）可逆传热：热平衡 （3）可逆相变：相平衡 （4）可逆化学反应：A ＋ B
E反＝E－dE + 电 池（E） A＋ B C -
C
可逆过程的重要性：（重要体会）
§2－4 热的计算 (How to calculate heat)
一、等容热 (Heat of isometric process)
2. 特点： (1) “双复原”：逆向进行之后系统恢复到 原状态，在环境中不留下影响。
Qr = −Q逆
Wr = −W逆
∴ 可逆过程进行之后，在系统和环境中产生 的后果能同时完全消失。 (2) 可逆意味着平衡：
T≈T环，p≈p外，动力无限小，速度无限慢。
(3) 等温可逆过程功值最大： W T , r > W T , ir
热力学物理量
状态函数 过程量
Ⅰ (过程量)
A
( (状态 函数) Ⅱ (过程量)
B
(状态 函数) )
(1) Ⅰ和Ⅱ的过程量一般不同：QⅠ≠ QⅡ， WⅠ≠ WⅡ Ⅰ和Ⅱ的状态函数变化相同：∆YⅠ＝ ∆YⅡ (2) 一般Q ≠-Q逆， W ≠-W逆； 但∆Y ＝- ∆Y逆
六、内能 (Internal energy) 动能 系统的能量 势能 机械能
V2 3 W = nRT ln = (3000 × 1 × ln )J = 3296J V1 1
可见，发生同样的状态变化，过程不同，功则不同 (热也不同)。
三、可逆过程 (Reversible process) 1. 定义：热力学的一类过程，其每一步都可以反 向进行而不在环境中引起其他变化。 上例：(2) 一次膨胀 W＝2000 J 反向(一次压缩) W逆＝3000×(1-3)＝-6000 J ∴ 在环境中留下影响。 (3) 可逆膨胀 W＝3296 J 反向(可逆压缩) W逆＝-3296 J ∴ 在环境中没有留下影响。
内能：定义，意义， 也称热力学能，U (1) U是状态函数：容量性质，U＝U(T, V) (2) 绝对值不可测
§2－2 热力学第一定律 (The First Law of Thermodynamics)
定律：能量守恒，叙述方法很多，第一 类永动机不可能。不需证明。 数学表达式：
dU = δ Q − δ W ∆U = Q − W