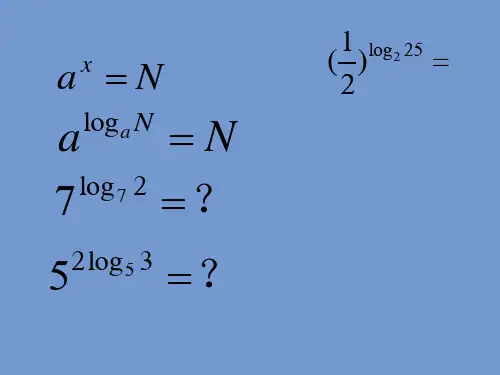当前位置：文档之家 › 新人教版高中数学幂函数PPT优秀课件2

新人教版高中数学幂函数PPT优秀课件2

  • 格式：ppt
  • 大小：1.15 MB
  • 文档页数：24

下载文档原格式

  / 24

合集下载

《幂函数》PPT课件

《幂函数》PPT课件

2 log2
1 22
1 2
练习2 :已知f ( x) m m 1 x
2


m 3
是幂函数，
求m的值。
解 : 因为f ( x)是幂函数
m m 1 1
2
解之得: m 2或m 1
m 2或m 1
加条件 :已知f ( x) m m 1 x
2
（4）y 3
x
（3）y 2x
（5）y x 1 1 （6）y x
2
练习1：已知幂函数f(x)的图像经过点 （2，2）， 试求出这个函数的解析式。
证明: 设所求的幂函数为 yx 函数的图像过 (2， 2 )点

2 2 ,
α log2

f ( x)
1 x2
证明幂函数 f ( x) x 在［0，+∞）上是增函数.
用定义证明函数的单调性的步骤:
x x2 x1＞0 (1). 取数:设x1, x2是某个区间上任意二值，
(2). 作差: f(x2)－f(x1)， (3) 整理: (4). 分析 f(x1)－f(x2) 的符号； (5). 下结论.
yx
yx
2
1 -1 -1 O1
x
y
1 -1 O -1 1
R
x
[0，+∞） 偶函数
y
yx
yx
3
-1
1 -1
O
y 1
1
x
R
R
奇函数
1 2
1
-1 O 1 -1
x
[0，+∞） [0，+∞） (-∞,0)∪ (-∞,0)∪ (0,+∞) (0,+∞)

3.3 幂函数 课件(共48张PPT)高一数学必修第一册(人教A版2019)

3.3 幂函数 课件(共48张PPT)高一数学必修第一册(人教A版2019)
1
(3) 在区间(0, )上,函数y x, y x2 , y x3 , y x 2单调递增, 函数y x1单调递减;
(4) 在第一象限内, 函数y x1的图象向上与y轴无限接近,向右与x轴 无限接近.
学习新知 例 证明函数f ( x) x是增函数.
证明：函数的定义域是[0, ). x1, x2 [0, ), 且x1 x2 ,
[0,+∞)递增
(-∞,0)和(0,+∞) 递减
图象
公共点
(1,1) ( R) (0,0) ( 0时)
①为偶数, y x是偶函 数. ②为—奇—数, y x是奇函 数.
3.3 幂函数
02 幂函数的图象 与性质
应用新知 1 幂函数的概念
一般地,函数y=xα叫做幂函数,其中x是自变量,α是常数.
本节我们利用这些知识研究一类新的函数．
学习新知
先看几个实例： (1)如果卢老师以1元/kg的价格购买了某种蔬菜t千克，那么他需要支付
的钱数P=t元，这里P是t的函数；
(2)如果正方形的边长为a，那么正方形的面积S=a2，这里S是a的函数；
(3)如果立方体的棱长为b，那么立方体的体积V=b3，这里V是b的函数；
或
m＝0.
当
m＝2
时，f(x)＝
x
1 2
，图象过点(4,2)；
当
m＝0
时，f(x)＝
x
3 2
，图象不过点(4,2)，舍去．
综上，f(x)＝
x
1 2
.
能力提升 题型三：利用幂函数的单调性比较大小
【练习
3】已知幂函数
f(x)＝m2
2m
1
m 3
x2
的图象过点(4,2)．

高中数学人教A版必修1第二章 基本初等函数——幂函数(共14张PPT)

高中数学人教A版必修1第二章 基本初等函数——幂函数(共14张PPT)

f(x 1 )f(x2 )x 1x2(x 1x x 2 1 )+ (x x 2 1+x2)
x1 x2 x1 + x2
方法技巧:分子有理化
因 x 1 x 2 , x 为 1 , x 2 [ 0 , + ) 所 ,x 1 x 2 以 0 ,x 1 + x 2 0 ,
所 f(x 以 1 )f(x2 )即 , 幂 f(x) 函 x在 [0 数 ,+)上 的 .
课堂小结
(1) 幂函数的定义； (2)五个基本幂函数的图像画法及特征； (3) 幂函数的性质。
作业：P79习题2.3： 1，2，3。
谢谢指导
不知道自己缺点的人，一辈子都不会想要改善。成功的花，人们只惊慕她现时的明艳！然而当初她的芽儿，浸透了奋斗的泪泉，洒遍了牺牲的血雨。成功的条件在于勇气和 信乃是由健全的思想和健康的体魄而来。成功了自己笑一辈子，不成功被人笑一辈子。成功只有一个理由，失败却有一千种理由。从胜利学得少，从失败学得多。你生而有 前进，形如蝼蚁。你一天的爱心可能带来别人一生的感谢。逆风的方向，更适合飞翔。只有承担起旅途风雨，才能最终守得住彩虹满天只有创造，才是真正的享受，只有拚 活。知识玩转财富。志不立，天下无可成之事。竹笋虽然柔嫩，但它不怕重压，敢于奋斗、敢于冒尖。阻止你前行的，不是人生道路上的一百块石头，而是你鞋子里的那一 爱，不必呼天抢地，只是相顾无言。最值得欣赏的风景，是自己奋斗的足迹。爱的力量大到可以使人忘记一切，却又小到连一粒嫉妒的沙石也不能容纳。生活不可能像你想 不会像你想的那么糟。时间告诉你什么叫衰老，回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵，昨天的太阳，晒不干今天的衣裳。实现梦想往往是一个艰苦的坚持的 到位，立竿见影。那些成就卓越的人，几乎都在追求梦想的过程中表现出一种顽强的毅力。世界上唯一不变的字就是“变”字。事实胜于雄辩，百闻不如一见。思路决定出 细节决定成败，性格决定命运虽然你的思维相对于宇宙智慧来说只不过是汪洋中的一滴水，但这滴水却凝聚着海洋的全部财富；是质量上的一而非数量上的一；你的思维拥 所有过不去的都会过去，要对时间有耐心。人总会遇到挫折，总会有低潮，会有不被人理解的时候。如果你希望成功，以恒心为良友，以经验为参谋，以小心为兄弟，以希 个人不知道他要驶向哪个码头，那么任何风都不会是顺风。沙漠里的脚印很快就消逝了。一支支奋进歌却在跋涉者的心中长久激荡。上天完全是为了坚强你的意志，才在道 碍。拥有资源不能成功，善用资源才能成功。小成功靠自己，大成功靠团队。炫耀什么，缺少什么；掩饰什么，自卑什么。所谓正常人，只是自我防御比较好的人。真正的 防而又不受害。学习必须如蜜蜂一样，采过许多花，这才能酿出蜜来态度决定高度。外在压力增加时，就应增强内在的动力。我不是富二代，不能拼爹，但为了成功，我可 站在万人中央成为别人的光。人一辈子不长不短，走着走着，就进了坟墓，你是要轰轰烈烈地风光下葬，还是一把骨灰撒向河流山川。严于自律：不能成为自己本身之主人 他周围任何事物的主人。自律是完全拥有自己的内心并将其导向他所希望的目标的惟一正确的途径。生活对于智者永远是一首昂扬的歌，它的主旋律永远是奋斗。眼泪的存 伤不是一场幻觉。要不断提高自身的能力，才能益己及他。有能力办实事才不会毕竟空谈何益。故事的结束总是满载而归，就是金榜题名。一个人失败的最大原因，是对自 的信心，甚至以为自己必将失败无疑。一个人炫耀什么，说明内心缺少什么。一个人只有在全力以赴的时候才能发挥最大的潜能。我们的能力是有限的，有很多东西飘然于 之外。过去再优美，我们不能住进去；现在再艰险，我们也要走过去！即使行动导致错误，却也带来了学习与成长；不行动则是停滞与萎缩。你的所有不甘和怨气来源于你 你可以平凡，但不能平庸。懦弱的人只会裹足不前，莽撞的人只能引为烧身，只有真正勇敢的人才能所向披靡。平凡的脚步也可以走完伟大的行程。平静的湖面锻炼不出精 生活打造不出生活的强者。人的生命似洪水在奔流，不遇着岛屿、暗礁，难以激起美丽的浪花人生不怕重来，就怕没有将来。人生的成败往往就在于一念之差。人生就像一 为你在看别人耍猴的时候，却不知自己也是猴子中的一员！人生如天气，可预料，但往往出乎意料。人生最大的改变就是去做自己害怕的事情。如果不想被打倒，只有增加 你向神求助，说明你相信神的能力；如果神没有帮助你，说明神相信你的能力。善待自己，不被别人左右，也不去左右别人，自信优雅。活是欺骗不了的，一个人要生活得 象这杯浓酒,不经三番五次的提炼呵,就不会这样一来可口！生命不止需要长度，更需要宽度。时间就像一张网，你撒在哪里，你的收获就在哪里。世上最累人的事，莫过于 你感到痛苦时，就去学习点什么吧，学习可以使我们减缓痛苦。当世界都在说放弃的时候，轻轻的告诉自己：再试一次。过错是暂时的遗憾，而错过则是永远的遗憾！很多 结果，但是不努力却什么改变也没有。后悔是一种耗费精神的情绪后悔是比损失更大的损失，比错误更大的错误所以不要后悔。环境不会改变，解决之道在于改变自己。积 成功者的最基本要素。激情，这是鼓满船帆的风。风有时会把船帆吹断；但没有风，帆船就不能航行。即使道路坎坷不平，车轮也要前进；即使江河波涛汹涌，船只也航行 粹取出来的。浪费时间等于浪费生命。老要靠别人的鼓励才去奋斗的人不算强者；有别人的鼓励还不去奋斗的人简直就是懦夫。不要问别人为你做了什么，而要问你为别人 遥远的梦想和最朴素的生活，即使明天天寒地冻，金钱没有高贵，低贱之分。金钱在高尚人的手中，就会变得高尚；金钱在庸俗人手中，就会变得低级庸俗。涓涓细流一旦 大海也就终止了��

高中数学必修一(人教版)《3.3 幂函数》课件

高中数学必修一(人教版)《3.3 幂函数》课件

()
(2)幂函数的图象都不过第二、四象限．
()
(3)当幂指数 α 取 1,3，12时，幂函数 y＝xα 是增函数．
()
(4)若幂函数 y＝xα 的图象关于原点对称，则 y＝xα 在定义域内 y 随 x 的增大
而增大．
()
答案：(1)× (2)× (3)√ (4)×
2．已知幂函数的图象过点(2,4)，则其解析式为
(1)幂函数在第一象限内指数的变化规律：在第一象限内直线x＝1的右侧，图 象从上到下，相应的指数由大变小；在直线x＝1的左侧，图象从下到上，相应的 指数由大变小．
(2)幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限内，至 于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时 出现在两个象限内；如果幂函数的图象与坐标轴相交，则交点一定是原点．
[典例 2] 若点( 2，2)在幂函数 f(x)的图象上，点－2，14在幂函数 g(x)的 图象上，问：当 x 为何值时，(1)f(x)＞g(x)？(2)f(x)＝g(x)？(3)f(x)＜g(x)?
[解] 设 f(x)＝xα，因为点( 2，2)在幂函数 f(x)的图 象上，所以将点( 2，2)代入 f(x)＝xα 中，得 2＝( 2)α， 解得 α＝2，则 f(x)＝x2.同理可求得 g(x)＝x－2.
解得 1≤a<32.
故 m 的值为 1，满足条件 f(2－a)>f(a－1)的实数 a 的取值范围为1，32.
[方法技巧] 解决幂函数的综合问题，应注意以下两点
(1)充分利用幂函数的图象、性质解题，如图象所过定点、单调性、奇 偶性等．
(2)注意运用常见的思想方法解题，如分类讨论思想、数形结合思想．
(1)依据图象高低判断幂指数大小，相关结论为：在(0,1)上，指数越大，幂函 数图象越靠近x轴(简记为指大图低)；在(1，＋∞)上，指数越大，幂函数图象越远 离x轴(简记为指大图高)．

3.3幂函数(共43张PPT)

3.3幂函数(共43张PPT)

解决幂函数图象问题应把握的原则 (1)依据图象高低判断幂指数大小，相关结论为：①在(0，1)上，指数越大， 幂函数图象越靠近 x 轴(简记为指大图低)；②在(1，＋∞)上，指数越大，幂 函数图象越远离 x 轴(简记为指大图高). (2)依据图象确定幂指数 α 与 0，1 的大小关系，即根据幂函数在第一象限内 的图象(类似于 y＝x－1 或 y＝x12或 y＝x3)来判断.
()
解析：选 D.由题意设 f(x)＝xn， 因为函数 f(x)的图象经过点(3， 3)， 所以 3＝3n，解得 n＝12， 即 f(x)＝ x， 所以 f(x)既不是奇函数，也不是偶函数， 且在(0，＋∞)上是增函数，故选 D.
4.函数 y＝x－3 在区间[－4，－2]上的最小值是_____________. 解析：因为函数 y＝x－3＝x13在(－∞，0)上单调递减， 所以当 x＝－2 时，ymin＝(－2)－3＝(－12)3＝－18. 答案：－18
B.－3 D.3
()
【解析】 (1)②⑦中自变量 x 在指数的位置，③中系数不是 1，④中解析式 为多项式，⑤中底数不是自变量本身，所以只有①⑥是幂函数.
(2)因为函数 y＝(m2＋2m－2)xm 为幂函数且在第一象限为增函数，所以 m2＋2m－2＝1， m>0， 所以 m＝1.
【答案】 (1)B (2)A
所以( 2)－32＞( 3)－32.
6
6
6
6
(3)因为 y＝x5为 R 上的偶函数，所以(－0.31)5＝0.315.又函数 y＝x5为[0，
＋∞)上的增函数，且 0.31＜0.35，
6
6
6
6
所以 0.315＜0.355，即(－0.31)5＜0.355.

人教高中数学B版必修二 《幂函数》指数函数、对数函数与幂函数PPT课件

人教高中数学B版必修二 《幂函数》指数函数、对数函数与幂函数PPT课件
人教高中数学B版必修二 《幂函数》指数函数、对数函数与幂函数PPT课 件
科 目：数学
适用版本：人教高中数学B版
适用范围：【教师教学】
4.4 幂函数
第一页，共三十一页。
第四章 指数函数、对数函数与幂函数
考点
学习目标
核心素养
了解幂函数的概念，会求幂函数 幂函数的概念
的解析式
数学抽象
结合幂函数 y＝x，y＝x2，y＝x3，
(－∞，0)
R 上__增___
[0，＋∞) 上__增__
上__减__ [0，＋∞)
上_增__
__(1_，__1_)__
R上 _增___
(－∞，0) 上__减___
(0，＋∞) 上__减___第七页，共三十一页。判断正误(正确的打“√”，错误的打“×”) (1)函数 y＝x－45是幂函数．( √ ) (2)函数 y＝2－x 是幂函数．( × ) (3)幂函数的图像都不过第二、四象限．( × )
值域
R [0，＋∞)
y＝x2 R
_(0_，__＋__∞__)
y＝x3 R R
y＝x－1
(_－__∞__，__0_)_∪_ (_0_，__＋__∞__) (－∞，0) ∪(0，＋∞)
第六页，共三十一页。
函数 性质
y＝x
1
y＝x2
y＝x2
y＝x3 y＝x－1
奇偶性
奇
非奇非偶 _偶___
__奇__
奇
单调性 公共点
第十二页，共三十一页。
(1)本题在求解中常因不理解幂函数的概念而找不出“m2－m－1＝ 1”这一等量关系，导致解题受阻． (2)幂函数 y＝xα(α∈R)中，α 为常数，系数为 1，底数为单一的 x. 这是判断一个函数是否为幂函数的重要依据和唯一标准．幂函数与 指数函数的解析式形同而实异，解题时一定要分清，以防出错．

幂函数教学讲解ppt课件

幂函数教学讲解ppt课件

03
幂函数的运算性质及应用
幂函数的加法、减法、乘法运算性质
总结词：掌握幂函数的基本运算性质是 理解幂函数应用的基础。
3. 幂函数的乘法运算性质： $(a^m)(a^n)=a^{m+n}$
2. 幂函数的减法运算性质：$(a^m)(a^n)=a^m-a^n$
详细描述
1. 幂函数的加法运算性质： $(a^m)+(a^n)=a^m+a^n$
课堂练习题
练习1：求解下列函数的奇 偶性
$y=x^2,x \in (-1,1)$；
$y=x^3,x \in (-1,1)$。
解析：对于$y=x^2,x \in (1,1)$，因为$-1<x<1$，所 以$-x<-1<1$，因此有$f(x)=(-x)^2=x^2=f(x)$，即 该函数为偶函数；对于 $y=x^3,x \in (-1,1)$，因为 $-1<x<1$，所以$-x<1<1$，因此有$f(-x)=(x)^3=-x^3=-f(x)$，即该函 数为奇函数。
02
在日常生活中，我们经常遇到幂 函数的实例，例如人口增长、金 融投资、计算机科技等。
幂函数的概念及重要性
定义
形如y=x^n的函数称为幂函数， 其中x是自变量，n是实常数。
幂函数的重要性
掌握幂函数的性质和变化规律， 有助于解决各种实际问题，培养 数学思维和解决问题的能力。
学习目标与学习方法
学习目标
详细描述
介绍幂函数的阶乘定义，通过实例阐述排列组合的基本概念，例如，组合公式、 排列公式等。
幂函数的对数运算
总结词
掌握幂函数的对数运算性质
详细描述
说明幂函数与对数函数之间的关系，推导基于幂函数的对数运算法则，例如，log(a^b)=b*log(a)。

《幂函数》新教材PPT完美课件

《幂函数》新教材PPT完美课件

第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T) 第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T)
第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T) 第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T)
第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T) 第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T)
பைடு நூலகம்
第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T) 第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T)
第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T) 第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T)
第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T) 第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T)
第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T) 第三章 3.3幂函数--【新教材】人教A版（2 019） 高中数 学必修 第一册 课件(共 60张PP T)

第三章3.3幂函数PPT课件(人教版)

第三章3.3幂函数PPT课件(人教版)

1.幂函数的概念 一般地，函数 y=xα 叫做幂函数，其中x是自变量，α是常数. 2.幂函数的图象和性质
拓展：对于幂函数y＝xα(α为实数)有以下结论： (1)当α>0时，y＝xα在(0，＋∞)上单调递增；(2)当α<0时，y＝xα在(0，＋∞)上单 调递减；(3)幂函数在第一象限内指数的变化规律：在直线x＝1的右侧，图象从 上到下，相应的幂指数由大变小.
已知 n 取±2，±12四个值，则相应于 C1，C2，C3，C4 的 n 依次为(
)
A.－2，－12，12，2
B.2，12，－12，－2
C.－12，－2，2，12
D.2，12，－2，－12
解析 根据幂函数 y＝xn 的性质，在第一象限内的图象当 n>0 时，n 越大，y＝xn
递增速度越快，故 C1 的 n＝2，C2 的 n＝12；当 n<0 时，|n|越大，曲线越陡峭，所
奇偶性 _奇___
_偶___
_奇___ __非__奇__非__偶__
__奇__
x∈[0，＋∞)， 单调性 _增___ __增__
x∈(－∞，0]， __减__
_增___
__增__
x∈(0，＋∞)，_减___ x∈(－∞，0)，_减___
公共点
都经过点（__1_，__1_）___
教材拓展补遗
[微判断] 1.函数y＝－x2是幂函数.( × )
【训练1】 若函数f(x)是幂函数，且满足f(4)＝16，则f(－4)的值等于________. 解析 设f(x)＝xα，因为f(4)＝16，∴4α＝16，解得α＝2，∴f(－4)＝(－4)2＝16. 答案 16
题型二 幂函数的图象及其应用 关键取决于α>0，α<0

人教版高中数学必修一2.3《幂函数》ppt课件

人教版高中数学必修一2.3《幂函数》ppt课件

奇函数 偶函数 奇函数 非奇非偶 奇函数
R上 增函数
(, 0)减 (0, ) 增
R上 增函数
[0, ) 增
(, 0) 减 (0, ) 减
（1,1）
幂函数性质
y y x3 y x2
4
1
yx
(1)函数 y x, y x2 , y x3, y x 2
3
1
y x1在(0,+∞)上都有定义，
培养学生数形结合、分类讨论的思想，以及分析归纳的 能力，培养学生合作交流的意识.
学习重点
从具体函数归纳认识幂函数的一些性质并简单应用.
学习难点
概括幂函数的性质.
问题情境
问题1：如果张红购买了每千克1元的水果w千克，
a 那么她需要付的钱数p＝ w 元，这里p是w的函数 y x
S 问题2：如果正方形的边长为a，那么正方形的面积
S= a 2 ， 这里S是a的函数
y x2
问题3：如果正方体的边长为a，那么正方体的体积
V
aa
S
V= a3 ，这里V是a的函数
y x3
问题4：如果正方形场地面积为S，那么正方形的边 1 1
长a= S 2 ，这里a是S的函数
y x2
问题5：如果某人ts内骑车行进了1km，那么他骑车
的速度 v = t 1 km/s. 这里v是t的函数
y y x3
4
y x2
(2,4)
yx
1
y x2 , y x3
3
1
2
y x2
1
-4
-3
-2
-1
o
(1,1)
1
2
y x1

幂函数ppt课件

幂函数ppt课件
∴(-3)3>(-π)3.
探究点四
幂函数性质的综合应用
【例4】 已知幂函数f(x)=
- 2 -2+3(-2<m<2,m∈Z)满足:
①f(x)在(0,+∞)上单调递增;
②对∀x∈R,都有f(-x)-f(x)=0.
求同时满足①②的幂函数f(x)的解析式,并求出x∈[1,4]时,f(x)的值域.
(2)函数f(x)=(m2-m-5)xm-1是幂函数,且在区间(0,+∞)上单调递增,试确定m的
值.
解 根据幂函数的定义,得m2-m-5=1,
解得m=3或m=-2.
当m=3时,f(x)=x2在区间(0,+∞)上单调递增;
当m=-2时,f(x)=x-3在区间(0,+∞)上单调递减,不符合要求.故m=3.
比较大小的两个实数必须在同一个函数的同一个单调区间内,否则无法比
较大小.
变式训练3 比较下列各组数的大小:
(1)
2 0.5
3 0.5
与
;
3
4
解 ∵y=x
0.5
3
在定义域上为增函数,又
4
>
2
2 0.5
3 0.5
,∴
<
.
3
3
4
(2)(-3)3与(-π)3.
解 ∵y=x3在定义域R上为增函数,又-3>-π,
值域
奇偶性
R
奇函数
在R上单
单调性
调递增
公共点 (1,1)
[0,+∞)
偶函数
奇函数
y=
既不是奇函数,
也不是偶函数
在[0,+∞)
上单调递增, 在R上单 在[0,+∞)上单

高一数学《幂函数》PPT课件

高一数学《幂函数》PPT课件

函数的性质不同
指数函数的底数是一个大于0且 不等于1的常数，而幂函数的底 数可以是任意实数。此外，指 数函数的值域为正实数集，而 幂函数的值域为非负实数集。
图像的形状不同
指数函数的图像是一条经过点 (0,1)的曲线，而幂函数的图像 是一条经过原点的曲线。
02
常见幂函数类型及其特点
一次幂函数
表达式
幂的乘方法则
幂的乘方
底数不变，指数相乘。公式： (a^m)^n = a^(m×n)
举例
(2^3)^4 = 2^(3×4) = 2^12； (x^2)^5 = x^(2×5) = x^10
积的乘方法则
积的乘方
把积的每一个因式分别乘方，再把所得的幂相乘。公式： (ab)^n = a^n × b^n
举例
在幂函数中，指数a可以取任意实数，但不同的a值会导致函数性质的不
同。学生需要注意区分不同a值对应的函数性质。
02 03
函数定义域
幂函数的定义域与指数a的取值有关。例如，当a≤0时，函数定义域为 非零实数集；当a>0且a为整数时，函数定义域为全体实数集。学生需 要注意根据指数a的取值来确定函数的定义域。
幂函数性质
幂函数的性质包括定义域、值域、奇偶性、单调性等。例如，当a>0时，幂函数在定义域内 单调递增；当a<0时，幂函数在定义域内单调递减。
幂函数图像
幂函数的图像根据a的不同取值而呈现出不同的形态，如直线、抛物线、双曲线等。通过图像 可以直观地了解幂函数的性质。
易错难点剖y = x^n（n为实数）
图像
02
一条直线（n=1时）或射线（n≠1时）
性质
03
当n>0时，函数在(0, +∞)上单调递增；当n<0时，函数在(0,

人教版高中数学必修一课件：2.3幂函数 (共24张PPT)

人教版高中数学必修一课件：2.3幂函数 (共24张PPT)
(2) y 1 x
(4) y x
1 2
(5) y=2x2 (6) y=x3+2
(3) y= -x2
思考：指数函数y=ax与幂函数y=xα有什么 区别？
二.幂函数与指数函数比较
名称 式子 指数函数: y=a
（a>0且a≠1)
x
常数 a为底数 α为指数
x
指数 底数
y
幂值 幂值
幂函数: y= xα
1
一般地，幂函数的图象 在直线x=1的右侧，大指 数在上，小指数在下， 在Y轴与直线x =1之间正 好相反。
练习：已知幂函数f(x)的图像经过点（3，27）， 求证：f(x)是奇函数。
证明 : 设所求的幂函数为
函数的图像过点
y x
( 3，27 )
3

27 3

,即 3
3
3

3
1
观察上述图象，将你发现的结论写在P78的表格内
(-2,4)
4
y= x 3
(2,4) y= x 2
3
y=x y= x
2
1 2
(4,2)
1
(-1,1)
(1,1) y= x -1
-6
-4
-2
-1
(-1,-1)
-2
-3
-4
在第一象限内， a >0,在(0,+∞)上为增函数; a <0,在(0,+∞)上为减函数. 幂函数的图象都通过点(1,1) a>0时,图象还都过点(0,0) α为奇数时,幂函数为奇函数, α为偶数时,幂函数为偶函数.
判断一个函数是幂函数还是指数函数切入点 看未知数x是指数还是底数 指数函数 幂函数

新课标人教版必修一幂函数课件(共11张PPT)

新课标人教版必修一幂函数课件(共11张PPT)
幂 函 数
代 兵
高中数学必修1同步辅导课程——幂函数
知识要点：
1：幂函数的定义：
一般地,函数y x 叫做幂函数, 其中x是自变量,

是常数.
注： 1 1.对于幂函数，我们重点讨论 =1，2，3， ,-1 2 时的情形。(对照教材，作出上述图像)
2.幂函数不同于指数函数和对数函数，其定义域
1
高中数学必修1同步辅导课程——幂函数
p x (0,1) 变式1： 时，函数 y x 的图像在直线 y x
上方，则P的取值范围是_________.
高中数学必修1同步辅导课程——幂函数
变式2:如果函数 f ( x) (m m 1) x
2
m2 ;∞ ）内是减函数，求满足条件 的实数m的集合。
１.所有的幂函数在(0,+∞)都有定义,并且函 数图象都通过点(1,1);
a>1 0<a<1
２.如果a>0,则幂函数的图象过点 (0,0),(1,1)并在(0,+∞)上为增函数;
a<0
３.如果a<0,则幂函数的图象过点(1,1), 并在(0,+∞)上为减函数; 其它象限的图像可由函数奇偶性对称作出
高中数学必修1同步辅导课程——幂函数
典型题例：
例1：若f(x)=(m2-3m+3)x3为幂函数,求m的值
解析：由题意： m2-3m+3=1 解得：m=1或4
高中数学必修1同步辅导课程——幂函数
例2：如图所示，曲线是幂函数 y = xa 在第一象
1 限内的图象，已知 a分别取 1,1, , 2 2
四个值，则相应图象依次为:________
高中数学必修1同步辅导课程——幂函数

幂函数课件ppt课件

幂函数课件ppt课件

课程总结回顾
幂函数的基本概念
回顾幂函数的基本定义，以及幂函数的图像和性质。
幂函数的运算规则
复习幂函数的加减乘除运算规则，以及幂函数运算的实例。
幂函数的实际应用
强调幂函数在生活和科学领域中的应用，如物理学、工程学、统 计学等。
对未来学习的展望和规划
深化对幂函数的理解
学习更高阶的数学理论
通过更多实例和习题，深化学生对幂函数 的理解和掌握。
幂函数乘法
$(x^m \times x^n) = x^{m+n}$
幂函数除法
$\frac{x^m}{x^n} = x^{m-n}$
幂函数的复合运算
复合幂函数
将多个幂函数进行复合运算，如：$((x^2+1)^3-2x^4)$
复合幂函数的运算顺序
先算括号内的幂函数，再乘除，最后加减
幂函数的求导与微分运算
金融和投资
在金融和投资领域，幂函数被用于描述股票价格的变化和收益率的 计算。
计算机科学
在计算机科学中，幂函数被用于高效计算大数和进行快速幂运算。
幂函数在物理学中的应用
描述放射性衰变
幂函数被用于描述放射性衰变的 过程，即原子核自发地转变为其
他原子核的过程。
描述药物代谢
在药理学中，药物的代谢过程通 常可以用幂函数来描述。
幂函数例子
如$y = 2^x$、$y = x^2$等均为幂函数。
幂函数的性质
奇偶性
当底数为正数时，幂函数为偶函 数；当底数为负数时，幂函数为
奇函数。
增减性
当指数为正数时，幂函数随着自变 量的增加而增加；当指数为负数时 ，幂函数随着自变量的增加而减小 。
零点
当指数为整数时，幂函数的零点为 该整数的负一次方。

幂函数教学(共43张PPT)高一数学人教B版必修第二册

幂函数教学(共43张PPT)高一数学人教B版必修第二册
R
R
奇函数
增函数
（5）如图所示中已经作出了函数 y＝x－1，y＝x，y＝x2 的图象，在其中作出函数 y＝x3 图象．
一般地，幂函数 y＝xα，随着 α 的取值不同，函数的定义域、值域、奇偶性、单调性也不尽相同，但也有一些共同的特征：（1）所有的幂函数在区间（0 , ＋∞）上都有定义，因此在第一象限内都有图象，并且图象都通过点（1 , 1）．
[0，＋∞）
非奇非偶函数
增函数
[0，＋∞）
根据以上信息可知，函数 的图象上的点，除了原点，其余点都在第一象限，通过描点（如左图所示），可作出其图象，如右图所示
给出研究函数 y＝x3 的性质与图象的方法，并用你的方法得出这个函数的性质：（1）定义域是___________；（2）值域是___________；（3）奇偶性是___________；（4）单调性是___________；
在关系式 N＝ab 中，以 a 为自变量、N 为因变量构造出来的函数 y＝xb 就是本节要讨论的幂函数.
我们以前学过函数 y＝x，y＝x2，y＝，这三个函数的解析式有什么共同的特点吗？你能根据指数运算的定义，把这三个函数的解析式改写成统一的形式吗？
幂函数
上面提到的函数 y＝x，y＝x2，y＝都是幂函数．
第四章 指数函数、对数函数与幂函数
4.4 幂函数
人教B版（2019）
课标要点
核心素养
1.了解幂函数的概念
数学抽象
2.了解五个常见幂函数的图象
直观想象
3.了解幂函数的图象与性质
逻辑推理
我们已经知道，在关系式 N＝ab 中，当底数 a 为大于 0 且不等于 1 的常数时；如果把 b 作为自变量、N 作为因变量，则 N 就是 b 的指数函数；如果把 N 作为自变量、b 作为因变量，则 b 就是 N 的对数函数（即 b＝logaN ）．那么，当 b 为常数时，是否可以将底数 a 作为自变量，N 作为因变量来构造函数关系呢？

3.3 幂函数 课件(37张)

3.3 幂函数 课件(37张)

[教材提炼]
预习教材，思考问题
函数 f(x)＝x、f(x)＝x2、f(x)＝1x，以前叫什么函数，它们有什么共同特征？
知识梳理 (1)一般地，函数__y_＝__x_α__叫做幂函数(power function)，其中 x 是自变量， α 是常数． (2)幂函数解析式的结构特征 ①指数为常数； ②底数是自变量，自变量的系数为 1； ③幂 xα 的系数为 1； ④只有 1 项．
若函数 f(x)＝(2m＋3)xm2－3 是幂函数，则 m 的值为( )
A．－1
B．0
C．1
D．2
解析：幂函数是形如 f(x)＝xα 的函数，所以 2m＋3＝1，∴m＝－1.
答案：A
探究二 幂函ቤተ መጻሕፍቲ ባይዱ的图象
[例 2] 幂函数 y＝x2，y＝x－1，y＝ 内的图象依次是图中的曲线( ) A．C2，C1，C3，C4 B．C4，C1，C3，C2 C．C3，C2，C1，C4 D．C1，C4，C2，C3
由题意得(a＋
.
∵y＝ 在(－∞，0)，(0，＋∞)上均单调递减， ∴a＋1＞3－2a＞0 或 0＞a＋1＞3－2a 或 a＋1＜0＜3－2a， 解得23＜a＜32或 a＜－1.
利用幂函数解不等式的步骤 利用幂函数解不等式，实质是已知两个函数值的大小，判断自变量的大小，常与 幂函数的单调性、奇偶性等综合命题．求解步骤如下： (1)确定可以利用的幂函数； (2)借助相应的幂函数的单调性，将不等式的大小关系，转化为自变量的大小关系； (3)解不等式求参数范围，注意分类讨论思想的应用．
[解析] y＝ ＝3 x2≥0，故只有 D 中的图象适合． [答案] D
3．如果一个函数 f(x)在其定义域内对任意 x，y 都满足 fx＋2 y≤12[f(x)＋f(y)]，则称这 个函数为下凸函数．下列函数：

3.3 幂函数-(新教材人教版必修第一册)(33张PPT)

3.3 幂函数-(新教材人教版必修第一册)(33张PPT)

性质，培养逻辑推
3．能利用幂函数的单调性比较指数幂的大小．(重点) 理的数学素养.
自主预习 探新知
1．幂函数的概念 一般地，函数 y＝xα 叫做幂函数，其中 x 是自变量， α 是常数． 2．幂函数的图象 在同一平面直角坐标系中，画出幂函数y＝x，y＝x2，y＝x3，y＝x12， y＝x－1的图象如图所示：
谢谢~
数．( )
(4)当幂指数α＝－1时，幂函数y＝xα在定义域上
是减函数．( )
2．幂函数的图象过点(2， 2)， 则该幂函数的解析式是( )
A．y＝x－1 B．y＝x12 C．y＝x2 D．y＝x3
B [设f(x)＝xα，则2α＝ 2， ∴α＝12，∴f(x)＝x12. 选B.]
3．函数 y＝x54的图象是( )
y＝x2＋x是两项和的形式，不是幂函数；
y＝1＝x0(x≠0)，可以看出，常函数y＝1的图象比幂函数y＝x0的图象
多了一个点(0,1)，所以常函数y＝1不是幂函数．
(2)设f(x)＝xα，∵f(4)＝3f(2)，∴4α＝3×2α，解得α＝log23，∴f12＝
12log23＝13.]
幂函数的图象及应用 【例2】 点( 2，2)与点－2，－12分别在幂函数f(x)，g(x)的图象 上，问当x为何值时，有： (1)f(x)>g(x)；(2)f(x)＝g(x)；(3)f(x)<g(x)．
m2＋2m－2＝1，
[解] 由题意得m2－1≠0， 2n－3＝0，
m＝－3， 解得n＝32，
所以m＝－3，n＝32.
判断一个函数是否为幂函数的方法 判断一个函数是否为幂函数的依据是该函数是否为y＝xαα为常数的 形式，即函数的解析式为一个幂的形式，且需满足：1指数为常数；2 底数为自变量；3系数为1.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
考察y=x0.3在区间(0,+ ∞)上为增函数
因为 0.2<0.3 所以 0.20.3<0.30.3 ②再比较0.30.3，0.30.2的大小
考察y=0.3x 所以在R上为减函数 因为 0.3>0.2 所以 0.30.3<0.30.2
所以 0.20.3 < 0.30.3 < 0.30.2 11
三.函数的奇偶性
2
我们学过一次函数，二次函数，反比例函数
如 yx,y1,yx2 x
它们在形式上有什么异同?
相同：函数解析式是幂的形式，且指数是常数， 底数是自变量.
不同：指数不同
一.幂函数
1.幂函数概念 一般地，如果一个函数，底数是自变量x,指
数是常量 a ，即 y=xa ，这样的函数叫做幂函数.
注意:幂函数中的指数 a可以为任意实数.在
☆对奇函数、偶函数定义的说明:
(1) 函数具有奇偶性的前提是：定义域关于原点对称。
[-b,-a]
o [a ,b]
x
（2） 若f(-x)=－f(x),则f(x)为奇函数, 反之亦然。 若f(-x)= f(x) ，则f(x)为偶函数, 反之亦然。
（3） 当函数f(x)是奇函数或偶函数时,称函数具有奇偶性。
在（-，0]上的图象如图，你能试作出[0，+）内 的图象吗？
y
0
x
： 想一想 已知函数f(x)是定义在R上的奇函数，
在（-，0]上的图象如图，你能试作出 [0，+） 内的图象。
y
0
x
练习 1.判断下列函数的奇偶性：
(1) f (x) 3 ; (2)yx2,x(3,3]; x
(3)f(x)x23; (4)f(x)2(x1)21
（1）观察f(x)=x3的图象
奇函数定义： 一般地，图像关于原点
对称的函数叫作奇函数
在奇函数中，f(-x)和 f(x)的 绝对值相等，符号相反，即 A‘(-x,-y)
y y x3
A(x,y)
o
x
f(-x)= - f(x)
结论：函数f(x)=x3 的图像关于原点对 称。
思考:函数图象上横坐标互为相反数的 点的纵坐标有什么关系？
（2）观察函数f(x)=x2图像
偶函数定义:
y
f(x)=x2
一般地，图像关于y轴对称A’(-fx(,-yx)) 的函数叫作偶函数.
f(Ax)( x,y)
-x
o
x
x
在偶函数中， f(-x)和f(x)的值
相等，即 f(-x)= f(x)
结论：函数f(x)=x2
的图像关于y轴对称。
思考:函数图象上横坐标互为相反数的 点的纵坐标有什么关系？
例2 判断f(x)=-2x5和g(x)=x4+2的奇偶性.
解 因为在R上f(x)=-2x5,f(-x)=-2(-x)5=2x5,所以 f(x)=-f(-x),
于是f(x)是奇函数. 而g(x)=x4+2,g(-x)=(-x)4+2=x4+2,所以 g(x)=g(-x).
于是g(x)是偶函数.
： 想一想 已知函数f(x)是定义域为R的偶函数，
3.前者采取强制剥夺的办法；后者主 张渐进 的缓和 的办法 。前者 使矛盾 迅速激 化，引 发七国 之乱； 后者达 到了削 弱王国 ，使之 无力对 抗中央 的目的 。 4.不正确。七国之乱是西汉统治集团 内部争 夺中央 政权的 斗争， 是王国 问题发 展的必 然结果 ，无论 是“削 藩”还 是“推 恩”， 都触及 诸侯王 的利益 ，必定 引其反 抗。王 国问题 解决的 主要条 件，一 是景帝 的举措 得当， 二是汉 武帝统 治时的 强盛。 如果没 有上述 举措， 单靠“ 推恩” 是不会 奏效的 。
3.下图中，只画出了函数图像的一半，请你画 出它们的另一半，并说出画法的依据.
小结
幂函数
y x 常数
自变量
奇函数 奇 偶 性
偶函数
f(x)=-f(-x) 图像关于原点对称
f(x)=f(-x)
图像关于y轴对称
1.汉朝实行郡国并行制，后来王国势 力膨胀 ，汉景 帝至汉 武帝时 逐步削 弱王国 ，加强 了中央 集权； 汉武帝 后期， 实行刺 史制， 加强对 诸侯和 地方高 官的监 察，东 汉末逐 渐演变 为地方 行政区 。 2.唐朝中后期，地方军镇节使越设越 多，权 力增长 ，形成 藩镇割 据的局 面。
(3) y= -x2
(6) y=(2x)3
2.幂函数y=f(x)的图像过点(2,8),求函数的解析式.
答案：y=x3
例1 画出函数f(x)=x3的图像，讨论其单调性.
解 :（1）列表
y
8
x … -2 -1 1 0 1 1 2 …
2
2
6
y … -8 -1 1
8
01
8
1 8…
4
2
（2）描点（3）连线
自测xm＋2
是幂函数且函数
f(x)为
偶函数，求 m 的值．
栏
解析：∵f(x)＝(m2－3m＋3)xm＋2是幂函数，∴m2－3m＋3＝1，目 链 即m2－3m＋2＝0，∴m＝1或m＝2.当m＝1，f(x)＝x3为奇函数，不 接 符合题意；当m＝2时，f(x)＝x4为偶函数，符合题意，∴m＝2.
x
-2
增减性 y=x3是R上的增函数 -4
-6
-8
学生活动： 请在同一坐标系中画出
1
yx,yx2,yx1,yx2
的图像，观察图像特别是第一象限 的特征，你有何发现？
y=x2 y=x3
y=x
1
y=x2
y=x-1
9
基础 梳理
递增 递减
(1,1) (0,0)和(1,1)
练习：比较下列三个值的大小
0.20.3 ，0.30.3 ，0.30.2 解：①先比较0.20.3，0.30.3 的大小
中学阶段我们只关注a=1，2，3，-1，1/2
2.幂函数的特征：
（1） y=xa的系数是1 ；
（2） 底数为x而不是x的代数式，如2x或x-2等；
（3） 幂函数y=xa中指数a确定则幂函数确定。
练习：
1.判断下列函数是否为幂函数.
(1) y=x4
(4)y(x2)3
(2)yx2x1
(5) y=x-5
方法一：根据函数的图象,判断其奇偶性.
(1)y3 奇函数 x
(2)yx2,x(3,3]
非奇非偶
(3)yx23 (4)y2(x1)21
偶函数
y
oy
非奇非偶
y
y
1
o
x -3 o 3 x o x -1 o x
-3
方法二 根据定义,判断其奇偶性.
(1)y3 (2)yx2,x(3,3] x
(3)yx23 (4)y2(x1)21
教学目标
1.了解幂函数的概念；能够通过观察总结简单 幂函数的一些性质；会利用定义判断或证明简 单函数的奇偶性。 2.了解利用奇偶性画函数图像和研究函数的方 法。 3.培养从特殊归纳出一般的意识，培养利用图 像研究函数奇偶性的能力，引导学生发现数学 中的对称美。 教学重点：幂函数的概念；奇偶函数的概念 教学难点：简单幂函数的图像、性质；正确判 断函数的奇偶性。