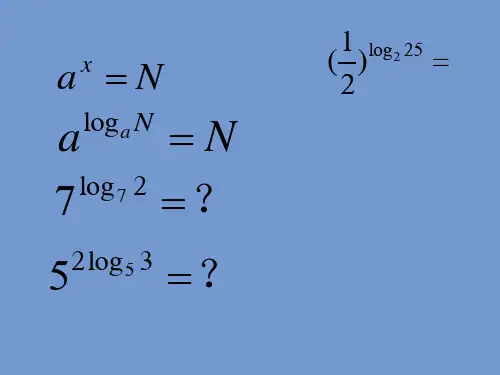03
幂函数的运算性质及应用
幂函数的加法、减法、乘法运算性质
总结词:掌握幂函数的基本运算性质是 理解幂函数应用的基础。
3. 幂函数的乘法运算性质: $(a^m)(a^n)=a^{m+n}$
2. 幂函数的减法运算性质:$(a^m)(a^n)=a^m-a^n$
详细描述
1. 幂函数的加法运算性质: $(a^m)+(a^n)=a^m+a^n$
课堂练习题
练习1:求解下列函数的奇 偶性
$y=x^2,x \in (-1,1)$;
$y=x^3,x \in (-1,1)$。
解析:对于$y=x^2,x \in (1,1)$,因为$-1<x<1$,所 以$-x<-1<1$,因此有$f(x)=(-x)^2=x^2=f(x)$,即 该函数为偶函数;对于 $y=x^3,x \in (-1,1)$,因为 $-1<x<1$,所以$-x<1<1$,因此有$f(-x)=(x)^3=-x^3=-f(x)$,即该函 数为奇函数。
02
在日常生活中,我们经常遇到幂 函数的实例,例如人口增长、金 融投资、计算机科技等。
幂函数的概念及重要性
定义
形如y=x^n的函数称为幂函数, 其中x是自变量,n是实常数。
幂函数的重要性
掌握幂函数的性质和变化规律, 有助于解决各种实际问题,培养 数学思维和解决问题的能力。
学习目标与学习方法
学习目标
详细描述
介绍幂函数的阶乘定义,通过实例阐述排列组合的基本概念,例如,组合公式、 排列公式等。
幂函数的对数运算
总结词
掌握幂函数的对数运算性质
详细描述
说明幂函数与对数函数之间的关系,推导基于幂函数的对数运算法则,例如,log(a^b)=b*log(a)。