最大流与最小费用流

§7 最大流问题7.1 最大流问题的数学描述 7.1.1 网络中的流定义 在以V 为节点集，A 为弧集的有向图),(A V G =上定义如下的权函数：（i ）R A L →:为孤上的权函数，弧A j i ∈),(对应的权),(j i L 记为ij l ，称为孤),(j i 的容量下界（lower bound ）；（ii ）R A U →:为弧上的权函数，弧A j i ∈),(对应的权),(j i U 记为ij u ，称为孤),(j i 的容量上界，或直接称为容量（capacity ）；（iii ）R V D →:为顶点上的权函数，节点V i ∈对应的权)(i D 记为i d ，称为顶点i 的供需量（supply ／demand ）；此时所构成的网络称为流网络，可以记为),,,,(D U L A V N =。

由于我们只讨论A V ,为有限集合的情况，所以对于弧上的权函数U L ,和顶点上的权函数D ，可以直接用所有孤上对应的权和顶点上的权组成的有限维向量表示，因此D U L ,,有时直接称为权向量，或简称权。

由于给定有向图),(A V G =后，我们总是可以在它的弧集合和顶点集合上定义各种权函数，所以流网络一般也直接简称为网络。

在流网络中，弧),(j i 的容量下界ij l 和容量上界ij u 表示的物理意义分别是：通过该弧发送某种“物质”时，必须发送的最小数量为ij l ，而发送的最大数量为ij u 。

顶点V i ∈对应的供需量i d 则表示该顶点从网络外部获得的“物质”数量（0>i d 时），或从该顶点发送到网络外部的“物质”数量（0<i d 时）。

下面我们给出严格定义。

定义 对于流网络),,,,(D U L A V N =，其上的一个流（flow ）f 是指从N 的弧集A 到R 的一个函数，即对每条弧),(j i 赋予一个实数ij f （称为弧),(j i 的流量）。

如果流f 满足∑∑∈∈∈∀=-Ai j j i ji A j i j ij V i d f f ),(:),(:,,（1）A j i u f l ij ij ij ∈∀≤≤),(,， （2）则称f 为可行流（feasible flow ）。

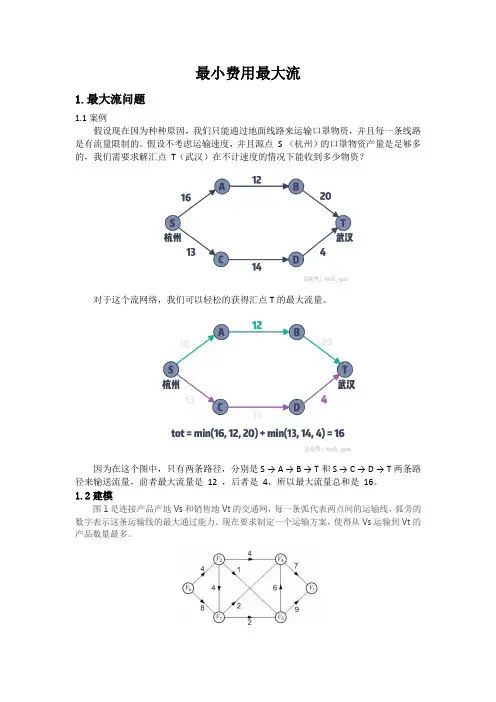
最小费用最大流1.最大流问题1.1案例假设现在因为种种原因，我们只能通过地面线路来运输口罩物资，并且每一条线路是有流量限制的。

假设不考虑运输速度，并且源点S （杭州）的口罩物资产量是足够多的，我们需要求解汇点T（武汉）在不计速度的情况下能收到多少物资？对于这个流网络，我们可以轻松的获得汇点T的最大流量。

因为在这个图中，只有两条路径，分别是S → A → B → T和S → C → D → T两条路径来输送流量，前者最大流量是12 ，后者是4，所以最大流量总和是16。

1.2建模图1是连接产品产地Vs和销售地Vt的交通网，每一条弧代表两点间的运输线，弧旁的数字表示这条运输线的最大通过能力。

现在要求制定一个运输方案，使得从Vs运输到Vt的产品数量最多。

图1模型():(,):(,)max .,,,,s ,0,s.t 0,,V V st f c Vf f t f Vμυμυμυυμυυυμμυλμυμυλμλμμμυ∈∈≤∀∈⎧=⎪-=-=⎨⎪≠⎩≥∀∈∑∑其中λ表示总共运输量f μυ表示弧(),μυ中的实际流量(),c μυ表示弧(),μυ中的容量限制S,t 表示物质运输的起点和终点最大流问题的推广现实问题中的网络，不但边有容量，而且点也有容量。

例如运 输网络中表示中转站的点v, 点容量 c(v) 可表示该中转站能容纳的货物的数列。

对点有容量的网络 N ，流函数若满足对一点 v,流入v 的流量之和等于流出v 的流量之和，并且小于等于c(v),2.最小费用最大流问题上面我们介绍了一个网络上最短路以及最大流的算法，但是还没有考虑到网络上流的费用问题，在许多实际问题中，费用的因素很重要。

例如，在运输问题中，人们总是希望在完成运输任务的同时，寻求一个使总的运输费用最小的运输方案。

这就是下面要介绍的最小费用流问题。

在运输网络N = (s,t,V, A,U)中，设(),c μυ是定义在A上的非负函数，它表示通过弧(),μυ单位流的费用。

最大流与最小费用流前两个星期都在看最大流与费用流，在找标程时几乎所有的都是C++的，少数几个Pascal的，要么代码风格乱七八糟，要么是不含任何优化的，我照着其中一个写下来最后发现居然是错的！最后请教了cyx并摸索了他的C++代码，终于“修成正果”。

把自己的心得贴在这里，给那些跟我一样看不懂C的在最大流与费用流中探索的OIers一点小小的help，顺便给自己攒点人品（或许我该去转C了，毕竟要跟得上时代）。

最大流我写的是Dinic算法，因为找不到传说中特别高效的SAP，所以就将就一下。

事实上我写了几道最大流的题目，发现Dinic效率还是不错的，而且编程复杂度又低，在OI 中还是蛮实用的。

算法思想就是建立残留网络，每次找到在残留网络中的一条增广路进行增广，添加反向边的目的就是用来退流的（想想为什么？）。

而Dinic在这基础上进行改进，就是构建层次图，沿层次图进行多路增广（不懂的话详细看代码）。

程序如下：program maxflow;var E,w,pre:array[0..20000] of longint;pot,dist,q:array[0..10000] of longint;n,m,s,t,ans,L:longint;procedure add(a,b,c:longint); //用链式前向星存储beginE[L]:=b; //E数组存点w[L]:=c; //w数组存每条边的容量pre[L]:=pot[a]; //pre数组记录起点同样为a的前一条边pot[a]:=L; //pot数组为索引表inc(L) //数组要从0开始存，否则后面的xor会出错，我因这个调了2小时end;procedure init; //直接建立残留网络，不用存原图var i,a,b,c:longint;beginL:=0;fillchar(pre,sizeof(pre),255); //这两个数组要初始化为-1，与后面调用fillchar(pot,sizeof(pot),255); 对应readln(n,m);for i:=1 to m dobeginreadln(a,b,c);add(a,b,c); //在残留网络中添加一条a到b剩余容量为c的边add(b,a,0) //添加反向边end;s:=1; t:=n //s为源，t为汇end;function bfs:boolean; //宽搜进行构建层次图（到源点的最短距离），var k,head,tail:longint; 因为每条边在这的距离权值都一样（为1），begin 所以不用写成spfa，cyx所教Orzfillchar(q,sizeof(q),0);fillchar(dist,sizeof(dist),255); //初始化为-1，用于退出时的判定head:=1; tail:=2;q[head]:=s; dist[s]:=0;while head<tail do //不需要采用循环队列,显然每个点只入队一次begink:=pot[q[head]];while k<>-1 dobeginif (w[k]>0) and (dist[E[k]]=-1) thenbegindist[E[k]]:=dist[q[head]]+1;q[tail]:=E[k];inc(tail)end;k:=pre[k]end;inc(head)end;if dist[t]<>-1 then exit(true) //是否存在增广路else exit(false)end;function min(a,b:longint):longint;beginif a>b then min:=b else min:=aend;function dfs(now,flow:longint):longint; //now为当前到达的节点，var k,tmp:longint; flow为当前可增广的最大流beginif now=t then exit(flow); //到达汇点，返回最大流dfs:=0;k:=pot[now];while k<>-1 dobeginif (w[k]>0) and (dist[E[k]]=dist[now]+1) then //判断边是否可走，begin 是否在层次图上tmp:=dfs(E[k],min(flow,w[k])); //深搜得到最大值并进行处理inc(dfs,tmp); （Dinic的多路增广）dec(flow,tmp);dec(w[k],tmp);inc(w[k xor 1],tmp); //利用xor进行关于对应边的高效处理if flow=0 then break //当前可增广流量为0，跳出end;k:=pre[k]endend;procedure dinic; //不断搜索路径进行增广beginwhile bfs doans:=ans+dfs(s,1 shl 31-1)end;procedure print;beginwriteln(ans)end;beginassign(input,'maxflow.in');assign(output,'maxflow.out');reset(input);rewrite(output);init;dinic;print;close(input);close(output)end.最小费用流算法其实可以说是一种贪心算法，每次找到一条费用最小的增广路进行增广，直到找不到增广路。