混合策略纳什均衡
- 格式:ppt
- 大小:405.50 KB
- 文档页数:34



混合策略纳什均衡名词解释
嘿,朋友们!今天咱来聊聊混合策略纳什均衡!这可不是什么晦涩难懂的概念哦。
想象一下,在一个竞争的场景里,就像一场激烈的游戏,大家都在绞尽脑汁地想着怎么出招。
混合策略纳什均衡呢,就是在这种情况下,各方参与者都没办法通过单独改变自己的策略来获得更好的结果。
它就好像是一场微妙的平衡舞蹈!每个人都要在不同的选择之间跳跃,找到那个最合适的组合。
不是单纯地选择一个固定的策略,而是有时候这样,有时候那样,让对手捉摸不透。
好比是下棋,你不能总是走同样的几步,得灵活多变,根据对手的反应随时调整。
而且啊,这个均衡可不是那么容易达到的哦,需要各方参与者不断地试探、博弈。
它不是那种一眼就能看穿的简单玩意儿,而是隐藏在复杂的互动之中。
就像在迷雾中寻找方向,需要耐心和智慧。
在现实生活中,混合策略纳什均衡也无处不在呢!商业竞争中,企业要考虑怎么定价、怎么推广,不就是在寻找这种微妙的平衡吗?政治博弈中,各方势力也在不断调整策略,试图达到对自己最有利的状态。
甚至在我们的日常生活中,比如和朋友玩游戏,或者在一些选择中纠结,都能看到混合策略纳什均衡的影子。
它让我们明白,有时候没有绝对的最佳策略,只有在不断变化中找到的相对平衡。
混合策略纳什均衡就是这么神奇,这么有趣!它让我们看到了竞争和互动的复杂性,也让我们更加懂得如何在各种情况下做出明智的选择。
所以啊,别小瞧了这个概念,它可是有着大用处呢!。

混合策略纳什均衡例子混合策略纳什均衡是博弈论中的一个重要概念,指的是各参与者选择一个概率分布作为他们的策略,从而达到一个稳定的状态。
在混合策略纳什均衡中,没有任何参与者可以通过单独改变自己的策略来获得更好的结果。
一个经典的混合策略纳什均衡的例子是“岩石-剪刀-布”游戏。
在这个游戏中,两个参与者(称为玩家1和玩家2)可以选择出岩石、剪刀或布中的任意一种。
每一种选择都有一定的胜负规则:岩石胜剪刀,剪刀胜布,布胜岩石。
假设玩家1选择出岩石、剪刀和布的概率分别为p1、q1和r1,玩家2选择出岩石、剪刀和布的概率分别为p2、q2和r2。
两个玩家的利益可以用一个支付矩阵表示如下:| 岩石 | 剪刀 | 布-----------------------------岩石 | 0 | -1 | 1-----------------------------剪刀 | 1 | 0 | -1-----------------------------布 | -1 | 1 | 0在混合策略纳什均衡中,每个玩家选择的概率分布必须使得对于每一种选择,玩家都不希望改变自己的概率分布。
在这个例子中,我们可以通过计算来找到混合策略纳什均衡。
假设玩家1选择出岩石的概率为p1,则选择剪刀的概率为q1=1-p1-0=1-p1,选择布的概率为r1=0-0=0。
同样地,玩家2选择出岩石的概率为p2,则选择剪刀的概率为q2=1-p2-0=1-p2,选择布的概率为r2=0-0=0。
为了找到混合策略纳什均衡,我们需要检查每一种选择,并确保玩家对于每一种选择都不希望改变自己的概率分布。
在这个例子中,无论玩家1选择什么概率分布,玩家2都可以通过选择相应的概率分布来获得更好的结果。
所以,不存在一个混合策略纳什均衡。
总结起来,混合策略纳什均衡是博弈论中一种稳定的策略选择状态,即不存在任何参与者可以通过单独改变自己的策略来获得更好的结果。
岩石-剪刀-布游戏是一个经典的混合策略纳什均衡的例子,其中玩家的选择概率分布是关键因素。

博弈论混合策略纳什均衡名词解释博弈论混合策略纳什均衡是指在博弈论中,当参与者不能确定选
择某一个策略时,采取混合策略的情况下达到的均衡状态。
具体来说,混合策略是指在一个博弈中,参与者以一定的概率选
择不同的纯策略。
而纳什均衡是指在一个博弈中,参与者无法通过单
独改变自己的选择来获得更好的结果,即不存在任何参与者可以通过
改变自己的策略来让其他参与者不再选择当前策略。
混合策略纳什均衡是指游戏中所有参与者以一定的概率选择不同
的纯策略,并且这种概率分配对于所有参与者都是最优的。
也就是说,在混合策略纳什均衡下,参与者没有更好的选择可供其采取,而其他
参与者也没有更好的概率分配可供其选择。
拓展:
在博弈论中,还有许多其他类型的均衡概念,例如纯策略纳什均衡、帕累托均衡、部分均衡等等。
纯策略纳什均衡是指游戏中参与者
以确定性的纯策略进行选择,使得没有参与者可以通过改变其策略来
获得更好的结果。
帕累托均衡是指在一个博弈中,不存在可以改善任
何一个参与者的情况。
部分均衡是指只有某些参与者达到均衡状态,而其他参与者未达到均衡状态。
博弈论是研究决策制定者在相互影响下进行决策的数学工具。
通过分析不同的博弈策略和可能的结果,博弈论可以帮助我们理解冲突和合作的情况,并提供一些决策建议。

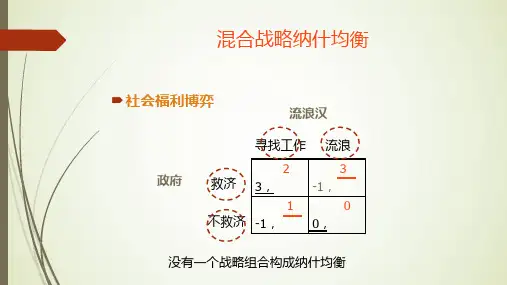



混合策略纳什均衡混合策略纳什均衡是博弈论中一个重要的概念。
纳什均衡是指在一个博弈中,每个参与者都选择了最优的策略,而且即使其他参与者知道其他参与者的策略,他们也无法从自己的策略中获得更大的利益。
而混合策略则是指参与者通过随机化选择不同策略的概率来达到最优策略。
本文将深入探讨混合策略纳什均衡的概念、特点以及计算方法。
首先,混合策略纳什均衡是指参与者通过一定概率选择不同策略的方式达到最优策略。
在混合策略中,每个参与者都拥有一个策略概率分布,表示他们在不同策略下的选择概率。
这样,在博弈中,每个参与者将根据其策略概率分布中的概率随机选择其中一种策略。
对于每个参与者而言,他们的目标是通过选择最优的策略概率分布来最大化自己的期望收益或最小化自己的期望损失。
其次,混合策略纳什均衡与纳什均衡相比具有以下特点。
首先,混合策略纳什均衡可以推翻完全信息博弈中的固定策略均衡结果。
在完全信息博弈中,参与者可以根据对其他参与者策略的了解来做出精确决策,因此均衡状态是唯一确定的。
而在混合策略博弈中,由于参与者通过概率选择不同策略,他们无法准确地预测其他参与者的策略,因此均衡状态不再是唯一确定的。
其次,混合策略纳什均衡可以引入不确定性,增加博弈的复杂性。
参与者无法准确地预测其他参与者的策略,因此他们需要通过一定的概率选择策略来平衡风险与收益。
最后,混合策略纳什均衡可以通过均衡态的共同选择来实现长期的稳定状态。
在混合策略纳什均衡中,参与者通过随机化选择策略,从而消除了其他参与者可以预测自己策略的可能性,增加了稳定性。
最后,计算混合策略纳什均衡的方法主要有以下两种。
一种是通过计算参与者的最优策略概率分布来确定混合策略纳什均衡。
这种方法主要基于线性规划技术,通过最大化或最小化参与者的期望收益或损失来确定最优的策略概率分布。
另一种方法是通过迭代算法来求解混合策略纳什均衡。
这种方法主要是通过反复更新参与者的策略概率分布,直到达到均衡状态。
混合策略纳什均衡计算方法(一)混合策略纳什均衡计算方法什么是混合策略纳什均衡混合策略纳什均衡是博弈论中的一个概念,指的是每个玩家都选择一定的概率来执行每一个可行的行动。
这样,游戏的结果不再是唯一的,而是有一定的概率分布。
如何计算混合策略纳什均衡计算混合策略纳什均衡需要用到线性规划的方法,具体步骤如下:1.确定每个玩家的策略空间,即每个玩家可选的所有策略。
2.建立概率分布矩阵,即每个玩家选择每个策略的概率。
3.利用概率分布矩阵和游戏的收益矩阵计算出每个玩家的期望收益。
4.建立线性规划模型来最大化每个玩家的期望收益。
5.求解线性规划模型得到混合策略纳什均衡。
混合策略纳什均衡的应用混合策略纳什均衡在实际应用中有广泛的应用。
比如在围棋、国际象棋等棋类游戏中,人类选手常常会使用混合策略来应对对手的不确定性。
同时,在市场竞争、拍卖、投资等领域,混合策略也可以用来帮助决策者做出最优的决策。
总结混合策略纳什均衡是博弈论中的重要概念,在实际应用中具有广泛的应用前景。
计算混合策略纳什均衡需要用到线性规划的方法,但具体计算步骤并不复杂。
我们可以通过深入理解和应用混合策略纳什均衡,来帮助我们更好地应对不确定性和竞争。
混合策略纳什均衡的优势混合策略纳什均衡作为一种考虑不确定性的策略,相较于确定性策略有以下优势:1.能够应对对手的随机性,减小被对手利用的风险;2.能够在一定程度上改变游戏的结果分布,增加自己的收益,同时降低失败的风险。
混合策略纳什均衡的局限性尽管混合策略纳什均衡具有很多优点,但是也存在以下局限性:1.混合策略需要玩家具有一定的判断力和计算能力,否则可能难以计算出最优解;2.没有一个确定的策略来保证获胜,更多地要依靠概率和运气;3.当游戏中有多个混合策略纳什均衡时,玩家可能难以选择最优的策略。
结语混合策略纳什均衡是一个重要的博弈论概念,应用范围广泛。
尽管混合策略存在一些局限性,但是这并不妨碍我们充分应用这一理论来帮助我们在不确定性和竞争中取得更好的结果。
目录[隐藏]1 什么是混合策略纳什均衡2 解混合策略纳什均衡的方法3 混合策略纳什均衡的经典博弈——猜谜博弈[1]4 混合策略纳什均衡博弈与其他均衡的关系[1]5 参考文献[编辑][编辑][编辑]混合策略纳什均衡混合策略纳什均衡(Mixed Strategy Nash Equilibrium )什么是混合策略纳什均衡混合策略纳什均衡:在n 个参与人的博弈G={S 1 ,... S n ; u 1,...u n }中,混合策略组合构成一个纳什均衡,如果对于所有的i =1,2...,n 下式成立:也就是说,如果一个策略组合使任何一个参与人的策略都是相对于其他参与人的策略的最佳策略,这个策略就构成一个纳什均衡,不管这个策略是混合策略还是纯策略。
混合策略纳什均衡是面对其他博弈者选择的不确定性的一个理性对策,其主要特征是作为混合策略一部分的每一个纯策略有相同的期望值,否则,一个博弈者会选择那个期望值最高的策略而排除所有其他策略,这意味着原初的状态不是一个均衡。
解混合策略纳什均衡的方法1、最大化支付法:即最大化各个参与人的效用函数。
2、支付相等法:根据前面分析的猜硬币博弈中参与人的策略的思路,每个参与人的混合策略都使其余参与人的任何纯策略的期望支付相等,因此,解混合策略纳什均衡可以令参与人的各个纯策略支付相等,构成方程组求解。
混合策略纳什均衡的经典博弈——猜谜博弈[1]两个局中人A 、B 手里各拿一枚硬币,每人可以选择正面向上或反面向上,然后同时亮出,如果两枚硬币正反面相同,B 付给A1元钱,如果两枚硬币正反面不相同,A 付给B1元钱。
在这种情况下,局中人A 、B 如何选择呢?下图给出这个博弈的双变量收益矩阵。
这是一个两人零和博弈,在每一个结局中一方所得即为另一方所失,即两个局中人的收益之和恰好等于零。
在双变量收益矩阵中采用画线的方法,在这个博弈中找不到纯策略纳什均衡。
那么,猜谜博弈是否存在混合策略纳什均衡呢?1950年纳什证明了任何有限博弈都至少存在一个纳什均衡(包括纯策略纳什均衡和混合策略纳什均衡)。
混合策略纳什均衡简介混合策略纳什均衡是博弈论中的一个重要概念,用于描述多方参与的博弈情境中,每个参与者按照一定的概率分布选择不同的策略,使得任何人无法通过改变自己的策略来获得更好的结果。
在这种均衡状态下,每个参与者的预期收益最大化。
混合策略在传统的博弈理论中,参与者通常会选择一个确定性的策略来对抗其他参与者。
然而,在现实生活中,我们经常遇到的情况是,每个参与者都存在一定的不确定性和随机性,犹豫在不同的策略之间选择。
这时,混合策略就应运而生了。
混合策略是指参与者以一定的概率分布选择不同的策略来进行博弈。
例如,在一个石头剪刀布的游戏中,参与者可以以1/3的概率选择石头,1/3的概率选择剪刀,1/3的概率选择布。
这样的不确定性选择使得博弈更具有变数和策略性。
纳什均衡纳什均衡是由约翰·福布斯·纳什在20世纪50年代提出的一个概念,用于描述博弈理论中的均衡状态。
在纳什均衡中,每个参与者选择的策略都是最优的,即在其他参与者选择的策略下,自己无法通过改变策略来获得更好的收益。
通常情况下,纳什均衡是以确定性策略为基础进行定义的。
但是当参与者选择混合策略时,纳什均衡也可以被定义为每个参与者选择混合策略的概率分布,使得任何人都无法通过改变自己的概率分布来获得更高的收益。
混合策略纳什均衡的计算方法计算混合策略纳什均衡的方法主要是通过解析求解和数值求解两种方式。
解析求解解析求解是一种通过代数和数学推导的方式来找到混合策略纳什均衡的方法。
通过建立参与者的效用函数和概率分布函数等数学模型,应用最优化理论和微积分等数学工具,可以得到参与者的最优混合策略。
然而,解析求解的方法通常只适用于简单的博弈情境,并且求解过程繁琐复杂。
数值求解数值求解是一种通过计算机模拟和迭代计算的方式来找到混合策略纳什均衡的方法。
通过构建博弈模型,设定参与者的初始混合策略,然后通过迭代计算,逐渐优化参与者的混合策略,直到收敛到纳什均衡。