混合策略纳什均衡(上)2013

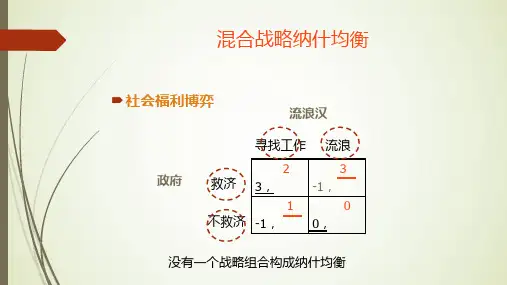
博弈论教学/混合策略的纳什均衡出自MyKnowledgeBase< 博弈论教学Bread crumbs: Main Page > 博弈论教学/混合策略的纳什均衡目录■1 复习■2 混合策略(Mixed strategy)■2.1 举例/Example■2.2 概念■2.3 纯策略和混合策略■2.4 混合策略的争议■3 混合策略的纳什均衡■3.1 基本概念■3.2 混合策略纳什均衡的存在性/纳什定理■3.3 学术争议与批评■4 混合策略纳什均衡举例■4.1 社会福利博弈Social Welfare Game■4.1.1 博弈分析(方法1:收益无差异)■4.1.2 博弈分析（方法2：图形分析法）■4.1.3 博弈分析(方法3：导数(Derivative)极值法)■4.2 普通例子■4.3 审计博弈(Tax Game)■4.4 激励的悖论[5]■4.5 求解纳什均衡的一般方法■5 多重纳什均衡■5.1 多重纳什均衡举例■5.1.1 夫妻之争■5.1.2 制式问题■5.1.3 市场机会博弈■5.2 多重纳什均衡分析■5.2.1 帕累托上策均衡（Pareto Dominated Equilibrium）■5.2.1.1 帕累托最优Pareto optimality■5.2.1.2 帕累托上策均衡(Pareto Dominated Equilibrium)■5.2.1.3 举例分析■5.2.2 风险上策均衡(Risk-dominant Equilibrium)■5.2.3 聚点均衡(Focal Points Equilibrium)■5.2.4 相关均衡■5.2.5 抗共谋均衡(coalition-proof Nash equilibrium)■6 纳什均衡的意义■7 作业■8 参考文献pure strategy）相对应。

混合策略：在博弈中，博弈方的策略空间为，则博弈方i以概率分布随机在其选策略中选择的“策略”，称为一个“混合策略”，其中，对都成立，且。

混合纳什均衡纳什均衡是指这样一种均衡：在这一均衡中，每个博弈参与人都确信，在给定其他参与人战略决定的情况下，他选择了最优战略以回应对手的战略。

”也就是说，所有人的战略都是最优的。

而讲解“纳什均衡”的最著名的案例就是“囚徒的困境”。

a,b两个囚徒，a坦白b抵赖，b判10年，a判1年.若两人均坦白则各判5年，若两人均抵赖则都判2年。

a，b 面临抉择。

显然最好的策略是双方都抵赖，结果是大家都只被判2年。

但是由于两人处于隔离的情况下无法串供，按照亚当·斯密的理论，每一个人都是一个“理性的经济人”，都会从利己的目的出发进行选择。

这两个人都会有这样一个盘算过程：假如他招了，我不招，得坐10年监狱，招了才5年，所以招了划算；假如我招了，他也招，得坐5年，他要是不招，我就只坐1年，而他会坐10年牢，也是招了划算。

综合以上几种情况考虑，不管他招不招，对我而言都是招了划算。

两个人都会动这样的脑筋，最终，两个人都选择了招，结果都被判5年刑期。

原本对双方都有利的策略(抵赖)和结局(被判1年刑)就不会出现。

这就是著名的“囚徒困境”。

它实际上反映了一个很深刻的问题，这就是个人理性与集体理性的矛盾。

混合策略均衡求解的一个原则是混合策略均衡赋予正概率的所有纯策略的期望收益相等。

假设这是个两个玩家的游戏。

玩家a有2种纯策略a和b，不能相互支配。

玩家b有2种纯策略c和d，不能相互支配。

设a选a的几率是p，则选b的几率为1-p；设b选c的几率是q，则选d的几率为1-q当a取某一个p=p0，b获得的总效用不为自己q的取值而改变；b取某一个q=q0，a获得的总效用不为自己p 的取值而改变，此时我们说（p0，1-p0）和（q0，1-q0）是一对混合策略下的纳什均衡。

混合策略纳什均衡：在n个参与人的博弈G={S1，...Sn;u1，...un}中，混合策略组合构成一个纳什均衡，如果对于所有的i=1，2...，n下式成立：也就是说，如果一个策略组合使任何一个参与人的策略都是相对于其他参与人的策略的最佳策略，这个策略就构成一个纳什均衡，不管这个策略是混合策略还是纯策略。

博弈论混合策略纳什均衡名词解释
博弈论是研究决策者在相互影响下进行决策的数学理论。

在博
弈中，混合策略指的是玩家以一定的概率分布来选择纯策略的组合，而纳什均衡是指在博弈中，每个玩家都采取最优的策略，假设其他
玩家的策略不变。

混合策略纳什均衡则是指在博弈中，玩家以一定
的概率分布来选择策略的组合，并且不存在其他策略组合可以使得
任何一个玩家通过改变自己的策略来获得更好的收益。

换句话说，
混合策略纳什均衡是玩家在采取混合策略的情况下达到的稳定状态，使得任何玩家都无法通过改变自己的策略来获得更好的结果。

混合
策略纳什均衡在博弈论中具有重要的理论和实际意义，可以帮助分
析和预测玩家在博弈中的最优决策行为，以及博弈过程中可能出现
的稳定状态。

在实际应用中，混合策略纳什均衡被广泛运用于经济学、政治学、生物学等领域，对于理解和解决实际问题具有重要的
指导意义。

条件混合策略的纳什均衡1. 引言嘿，大家好！今天咱们聊聊一个既有趣又有点深奥的话题——条件混合策略的纳什均衡。

听起来有点复杂？别担心，咱们用轻松的方式来聊，保证让你听得懂、记得住。

想象一下，你和你的朋友正在玩一个游戏，可能是扑克、棋类，或者甚至是猜拳。

这个游戏的关键在于，你的决策不仅仅取决于你自己的选择，还要考虑到对方的想法和选择。

这就是咱们今天要讲的核心——在不确定的情况下，怎样做出最优决策。

2. 纳什均衡简介2.1 什么是纳什均衡？那么，纳什均衡到底是个啥呢？简单说，就是一个状态，在这个状态下，任何一个玩家如果单独改变自己的策略，都会让自己变得更糟。

就像一场足球比赛，双方都在根据对方的表现调整策略，最终形成一种微妙的平衡。

你不动，我不动，大家都不动，这就是纳什均衡。

说白了，想要赢，你得懂得有时候不动也是一种策略。

2.2 条件混合策略接下来，咱们再说说“条件混合策略”。

乍一听，好像高深莫测，其实它就是在不同情况下随机选择不同的策略。

举个例子：想象你和朋友下棋，你可能在某一轮选择攻击，而在另一轮选择防守。

这种随机性可以让对手难以预测你的下一步动作，嘿，这就让游戏更有趣了，对吧？3. 条件混合策略的运用3.1 实际案例现在咱们把这个理论应用到实际中，看看它是如何运作的。

比如在商业竞争中，两家公司为了争夺市场份额，可能会在价格、广告和产品质量上进行博弈。

一家公司可能会在价格上采取“低价策略”，而另一家公司则可能选择“高价策略”，同时在广告上加大投入。

通过这样的条件混合策略，双方都可以在市场中找到一种平衡，既能保护自己的利益，又能不至于把对方逼得太狠。

3.2 生活中的例子不仅如此，这种策略在我们的日常生活中也屡见不鲜。

想象一下你和朋友一起去餐厅，点菜的时候总是考虑对方喜欢什么，而不是只顾着自己。

你可能今天想吃披萨，但考虑到对方可能更喜欢汉堡，你就故意“随机”选择一下，看看情况。

如果对方也点了披萨，嘿，你们就双赢了！这样的“条件混合策略”让你们的友谊更加稳固，岂不是一举两得？4. 结论通过上面的讨论，咱们发现，条件混合策略的纳什均衡不仅仅是个理论，还是生活中随处可见的智慧。

目录[隐藏]1 什么是混合策略纳什均衡2 解混合策略纳什均衡的方法3 混合策略纳什均衡的经典博弈——猜谜博弈[1]4 混合策略纳什均衡博弈与其他均衡的关系[1]5 参考文献[编辑][编辑][编辑]混合策略纳什均衡混合策略纳什均衡（Mixed Strategy Nash Equilibrium ）什么是混合策略纳什均衡混合策略纳什均衡：在n 个参与人的博弈G={S 1 ,... S n ; u 1,...u n }中，混合策略组合构成一个纳什均衡，如果对于所有的i ＝1，2...，n 下式成立：也就是说，如果一个策略组合使任何一个参与人的策略都是相对于其他参与人的策略的最佳策略，这个策略就构成一个纳什均衡，不管这个策略是混合策略还是纯策略。

混合策略纳什均衡是面对其他博弈者选择的不确定性的一个理性对策，其主要特征是作为混合策略一部分的每一个纯策略有相同的期望值，否则，一个博弈者会选择那个期望值最高的策略而排除所有其他策略，这意味着原初的状态不是一个均衡。

解混合策略纳什均衡的方法1、最大化支付法：即最大化各个参与人的效用函数。

2、支付相等法：根据前面分析的猜硬币博弈中参与人的策略的思路，每个参与人的混合策略都使其余参与人的任何纯策略的期望支付相等，因此，解混合策略纳什均衡可以令参与人的各个纯策略支付相等，构成方程组求解。

混合策略纳什均衡的经典博弈——猜谜博弈[1]两个局中人A 、B 手里各拿一枚硬币，每人可以选择正面向上或反面向上，然后同时亮出，如果两枚硬币正反面相同，B 付给A1元钱，如果两枚硬币正反面不相同，A 付给B1元钱。

在这种情况下，局中人A 、B 如何选择呢?下图给出这个博弈的双变量收益矩阵。

这是一个两人零和博弈，在每一个结局中一方所得即为另一方所失，即两个局中人的收益之和恰好等于零。

在双变量收益矩阵中采用画线的方法，在这个博弈中找不到纯策略纳什均衡。

那么，猜谜博弈是否存在混合策略纳什均衡呢?1950年纳什证明了任何有限博弈都至少存在一个纳什均衡(包括纯策略纳什均衡和混合策略纳什均衡)。

定义纳什均衡是一种策略组合，使得每个参与人的策略是对其他参与人策略的最优反应。

假设有n个局中人参与博弈，如果某情况下无一参与者可以独自行动而增加收益（即为了自身利益的最大化，没有任何单独的一方愿意改变其策略的），则此策略组合被称为纳什均衡.所有局中人策略构成一个策略组合（Strategy Profile）。

纳什均衡，从实质上说，是一种非合作博弈状态。

纳什均衡达成时，并不意味着博弈双方都处于不动的状态，在顺序博弈中这个均衡是在博弈者连续的动作与反应中达成的。

纳什均衡也不意味着博弈双方达到了一个整体的最优状态，以下的囚徒困境就是一个例子。

经济学定义所谓纳什均衡，指的是参与人的这样一种策略组合，在该策略组合上，任何参与人单独改变策略都不会得到好处。

换句话说，如果在一个策略组合上，当所有其他人都不改变策略时，没有人会改变自己的策略，则该策略组合就是一个纳什均衡。

Nash平衡是指博弈中这样的局面，对于每个参与者来说，只要其他人不改变策略，他就无法改善自己的状况。

Nash在证明了在每个参与者都只有有限种策略选择、并允许混合策略的前提下，Nash平衡一定存在。

以两家公司的价格大战为例，Nash平衡意味着两败俱伤的可能：在对方不改变价格的条件下，既不能提价，否则会进一步丧失市场；也不能降价，因为会出现赔本甩卖。

于是两家公司可以改变原先的利益格局，通过谈判寻求新的利益评估分摊方案，也就是Nash平衡。

类似的推理当然也可以用到选举，群体之间的利益冲突，潜在战争爆发前的僵局，议会中的法案争执等。

经典案例囚徒困境（1950年，数学家塔克任斯坦福大学客座教授，在给一些心理学家作讲演时，讲到两个囚犯的故事。

）假设有两个小偷A和B联合犯事、私入民宅被警察抓住。

警方将两人分别置于不同的两个房间内进行审讯，对每一个犯罪嫌疑人，警方给出的政策是：如果一个犯罪嫌疑人坦白了罪行，交出了赃物，于是证据确凿，两人都被判有罪。

如果另一个犯罪嫌疑人也作了坦白，则两人各被判刑8年；如果另一个犯罪嫌人没有坦白而是抵赖，则以妨碍公务罪（因已有证据表明其有罪）再加刑2年，而坦白者有功被减刑8年，立即释放。

混合策略纳什均衡简介混合策略纳什均衡是博弈论中的一个重要概念，用于描述多方参与的博弈情境中，每个参与者按照一定的概率分布选择不同的策略，使得任何人无法通过改变自己的策略来获得更好的结果。

在这种均衡状态下，每个参与者的预期收益最大化。

混合策略在传统的博弈理论中，参与者通常会选择一个确定性的策略来对抗其他参与者。

然而，在现实生活中，我们经常遇到的情况是，每个参与者都存在一定的不确定性和随机性，犹豫在不同的策略之间选择。

这时，混合策略就应运而生了。

混合策略是指参与者以一定的概率分布选择不同的策略来进行博弈。

例如，在一个石头剪刀布的游戏中，参与者可以以1/3的概率选择石头，1/3的概率选择剪刀，1/3的概率选择布。

这样的不确定性选择使得博弈更具有变数和策略性。

纳什均衡纳什均衡是由约翰·福布斯·纳什在20世纪50年代提出的一个概念，用于描述博弈理论中的均衡状态。

在纳什均衡中，每个参与者选择的策略都是最优的，即在其他参与者选择的策略下，自己无法通过改变策略来获得更好的收益。

通常情况下，纳什均衡是以确定性策略为基础进行定义的。

但是当参与者选择混合策略时，纳什均衡也可以被定义为每个参与者选择混合策略的概率分布，使得任何人都无法通过改变自己的概率分布来获得更高的收益。

混合策略纳什均衡的计算方法计算混合策略纳什均衡的方法主要是通过解析求解和数值求解两种方式。

解析求解解析求解是一种通过代数和数学推导的方式来找到混合策略纳什均衡的方法。

通过建立参与者的效用函数和概率分布函数等数学模型，应用最优化理论和微积分等数学工具，可以得到参与者的最优混合策略。

然而，解析求解的方法通常只适用于简单的博弈情境，并且求解过程繁琐复杂。

数值求解数值求解是一种通过计算机模拟和迭代计算的方式来找到混合策略纳什均衡的方法。

通过构建博弈模型，设定参与者的初始混合策略，然后通过迭代计算，逐渐优化参与者的混合策略，直到收敛到纳什均衡。