中职数学三角函数 1

第五章 三角函数㈠角、任意三角函数定义 1．角：2．弧度制：半径长的圆弧所对的圆心角为1弧度角。

180rad π︒=10.01745180rad rad π︒=≈ 180157.3rad π︒⎛⎫=≈︒ ⎪⎝⎭3．终边相同的角的表示：{}/360,k k z ββα=︒+∈ {}/2,k k z ββπα=+∈终边在坐标轴上的角的集合：x 正半轴：{}/2,k k z ααπ=∈ y 正半轴：/2,2k k z πααπ⎧⎫=+∈⎨⎬⎩⎭x 负半轴：{}/2,k k z ααππ=+∈ y 负半轴：3/2,2k k z πααπ⎧⎫=+∈⎨⎬⎩⎭x 轴： {}/,k k z ααπ=∈y 轴： /,2k k z πααπ⎧⎫=+∈⎨⎬⎩⎭坐标轴： /,2k k z παα⎧⎫=∈⎨⎬⎩⎭第一象限角 /22,2k k k z παπαπ⎧⎫<<+∈⎨⎬⎩⎭ 第二象限角/22,2k k k z παπαππ⎧⎫+<<+∈⎨⎬⎩⎭第三象限角 3/22,2k k k z παππαπ⎧⎫+<<+∈⎨⎬⎩⎭第四象限角3/222,2k k k z παπαππ⎧⎫+<<+∈⎨⎬⎩⎭ 4．任意角的三角函数：在角θ终边上任取一点P （x,y ）,0)r r =>正弦sin y r θ= 余弦cos x r θ= 正切tan yxθ=任意角三角函数符号：一全二正弦三切四余弦sin θ 全+ + tan θ θcos+ +5．同角三角函数关系sin tan cos θθθ=22sin cos 1θθ+= ()2sin cos 12sin cos αααα±=± 特殊勾股数：3，4，5； 6，8，10； 5，12，13； 8，15，17；7，24，25；㈣三角函数图像及性质 1．图像：2．性质：表格中的,k kz∈函数 名称定义域值域最小正周期奇偶性 单调性 最值点sin y x =R[]1,1-2π奇函数2,222k k ππππ⎡⎤-++↑⎢⎥⎣⎦32,222k k ππππ++↓⎡⎤⎢⎥⎣⎦2,12x k y ππ=+=2,12x k y ππ=-+=-cos y x =R[]1,1-2π 偶函数[]2,2k k πππ-+↑[]2,2k k πππ+↓2,1x k y π==2,1x k y ππ=+=-sin(),(,,)y A x A x R ωϕωϕ=+∈是常数 函数值域：[-A ，A]A 是振幅，最小正周期2T πω=，x ωϕ+是相位， 0x = 时，ϕ叫初相6sin sin 2sin(2)3sin(2)33y x y x y x y x πππ=−−−−−→=−−−−→=+−−−−−→=+横坐标变为向左纵坐标变为1原来的3倍平移原来的23sin sin()sin(2)3sin(2)333yx yx y x y x ππππ=−−−−→=+−−−−−→=++−−−−−→=+向左横坐标变为纵坐标变为1原来的3倍平移原来的2。

三角函数一、任意角1. 角的概念的推广 ⑴“旋转”形成角ABαO⑵“正角”与“负角”“0角”我们把按逆时针方向旋转所形成的角叫做正角，把按顺时针方向旋转所形成的角叫做负角，如图，以OA 为始边的角α＝210°，β＝－150°，γ＝660°。

2100-15006600特别地，当一条射线没有作任何旋转时，我们也认为这时形成了一个角，并把这个角叫做零角。

记法：角α或α∠ 可以简记成α。

2. “象限角”角的顶点合于坐标原点，角的始边合于x 轴的正半轴，这样一来，角的终边落在第几象限，我们就说这个角是第几象限的角（角的终边落在坐标轴上，则此角不属于任何一个象限） 3. 终边相同的角所有与α终边相同的角连同α在内可以构成一个集合。

{}Z k k S ∈⋅+==,360|οαββ二、弧度制1. 定义：长度等于半径长的弧所对的圆心角称为1弧度的角它的单位是rad ，读做弧度，这种用“弧度”做单位来度量角的制度叫做弧度制．说明：（1）正角的弧度数是正数，负角的弧度数是负数，零角的弧度数是0（2）角α 的弧度数的绝对值公式：lrα= （l 为弧长， r 为半径） 2. 角度制与弧度制的换算：∵ 360︒＝2π rad ∴180︒＝π rad∴ 1︒＝rad rad 01745.0180≈π'185730.571801οοο=≈⎪⎭⎫ ⎝⎛=πrad3. 两个公式1）弧长公式：α⋅=r l 由公式：⇒=r l α α⋅=r l 比公式180rn l π=简单 弧长等于弧所对的圆心角（的弧度数）的绝对值与半径的积 2）扇形面积公式 lR S 21=其中l 是扇形弧长，R 是圆的半径4. 一些特殊角的度数与弧度数的对应值应该记住： 角度 0° 30° 45° 60° 90° 120° 135° 150° 180° 弧度 0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π/6 π 角度 210° 225° 240° 270° 300° 315° 330° 360° 弧度7π/65π/44π/33π/25π/37π/411π/62π5. 应确立如下的概念：角的概念推广之后，无论用角度制还是弧度制都能在角的集合与实数的集合之间建立一种一一对应的关系正角 零角 负角正实数 零 负实数任意角的集合 实数集R三、任意角三角函数的定义1. 设α是一个任意角，在α的终边上任取（异于原点的）一点P （x ，y ） 则P 与原点的距离02222>+=+=y x yx rry)(x,α（1）把比值r y叫做α的正弦 记作： ry =αsin （2）把比值r x叫做α的余弦 记作： rx =αcos（3）把比值x y叫做α的正切 记作： xy =αtan上述三个比值都不会随P 点在α的终边上的位置的改变而改变.当角α的终边在纵轴上时，即Z)(2∈+=k k ππα时，终边上任意一点P 的横坐标x 都为0，所以tan α无意义；它们都是以角为自变量，以比值为函数值的函数.以上三种函数，统称为三角函数。

,180,270等。

．终边相同的角的集合：所有与角α终边相同的角，连同角说明：终边相同的角不一定相等，相等的角终边一定相同。

5.2弧度制 *回顾知识 复习导入 问题角是如何度量的？角的单位是什么？ 解决将圆周的1360圆弧所对的圆心角叫做1度角，记作1°． 1度等于60分（1°=60′），1分等于60秒（1′=60″）． 以度为单位来度量角的单位制叫做角度制． 扩展计算：23°35′26″+31°40′43″角度制下，计算两个角的加、减运算时，经常会带来单位换算上的麻烦．能否重新设计角的单位制，使两角的加、减运算像10进位制数的加、减运算那样简单呢？动脑思考 探索新知 概念将等于半径长的圆弧所对的圆心角叫做1弧度的角，记作1弧度或1rad ．以弧度为单位来度量角的单位制叫做弧度制．若圆的半径为r ，圆心角∠AOB 所对的圆弧长为2r ，那么∠AOB 的大小就是 22r r=弧度弧度．规定：正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零． 分析由定义知道，角α的弧度数的绝对值等于圆弧长l 与半径r 的比，即 lrα=（rad ）．半径为r 的圆的周长为2πr ，故周角的弧度数为2π(rad)2π(rad)rr=． 由此得到两种单位制之间的换算关系：360°=2πrad ，即 180°=πrad ．108；120︒≈200︒≈-60°=；30°=；120°=；270°=．2．把下列各角从弧度化为角度（口答）：π=；π2=；π4=；π8=；2π3=；π3=；π6=；π12=．3．把下列各角从角度化为弧度：⑴ 75°；⑵−240°；⑶ 105°；⑷67°30′．4．把下列各角从弧度化为角度：⑴π15；⑵2π5；⑶4π3-；⑷6π-．自我探索使用工具准备计算器．观察计算器上的按键并阅读相关的使用说明书，小组完成计算器弧度与角度转换的方法．利用计算器，验证计算例题1与例题2．巩固知识典型例题例3某机械采用带传动，由发动机的主动轴带着工作机的从动轮转动．设主动轮A的直径为100 mm，从动轮B的直径为280 mm．问：主动轮A旋转360°，从动轮B旋转的角是多少？（精确到1′）解主动轮A旋转360°就是一周，所以，传动带转过的长度为π×100 = 100π（mm）．再考虑从动轮，传动带紧贴着从动轮B转过100π(mm)的长度，那么，应用公式lrα=，从动轮B转过的角就等于'1005128341407π=π≈．答从动轮旋转5π7，用角度表示约为128°34′．例4如下图，求公路弯道部分AB的长l（精确到0．1m．图中长度单位：m）．4327123607=⨯+，所以，>，cos43270>，tan43270>．）因为2722π=⨯π7+5，所以，275π角为第三象限角，故0，cos，27tan．-+-；3sin902tan06sin270这类问题需要首先计算出界限角的三角函数值，然后再进行代3sin902tan06sin270-+--⨯+⨯-⨯-=-．31206(1)2强化练习5.3.3-++．5sin902cos03tan180cos180课堂教学安排主要教学内容及步骤教学过程师生活动设计意图等(一)复习诱导公式一师：我们已经学习过诱导公式一，即终边相同的角的同一三角函数的值相等，这组公式是如何表达的？它们的作用是什么？生：诱导公式一可这样表达：sin(2kπ+α)=sinα；cosα(2kπ+α)=cosα；tg(2kπ+α)=tgα；ctg(2kπ+α)=ctgα．利用诱导公式一可以把求任意角的三角函数值的问题，转化为求0°～360°(0～2π)间角的三角函数值的问题．师：学习诱导公式的基本思想方法是化归转化，如果我们能把求90°～360°间的角的三角函数值转化为求0°～90°间的角的三角函数值，那么任意角的三角函数值就都能通过查表来求．设0°≤α≤90°，则90°～180°间的角，可以写成180°-α；180°～270°间的角，可以写成180°+α；270°～360°间的角，可以写成360°-α．下面我们依次讨论180°+α，-α，180-α，360°-α的三角函数值与α的三角函数值之间的关系．为了使讨论更具有一般性，这里假定α为任意角．(布置学生阅读P．152—153初步了解诱导公式二、公式三的推导过程．)(二)诱导公式二、三师：首先我们先介绍单位圆概念，如图2-18示，以原点为圆心，等于单位长的线段为半径作一个圆，这样的圆称为单位圆．下面我们利用单位圆和任意角三角函数的定义来推导诱导公式二、三．推导之前，请一位同学回答分别关于x轴，y轴，原点对称的两个点的坐标间的关系．生：设点P(x、y)，它关于x轴、y轴、原点对称的点坐标分别是P1(x，-y)，P2(-x，-y)，P3(-x，-y)．师：请同学们作出一个任意角α的终边，再作出180°+α角的终边，它们与单位圆的交点有何特征？为什么？生：如图2-18，任意角α的终边与单位圆交于点P(x，y)．由于角180°+α的终边就是角α终边的反向延长线，角180°+α的终边与单位圆的交点P′，是与点P关于点O对称的。

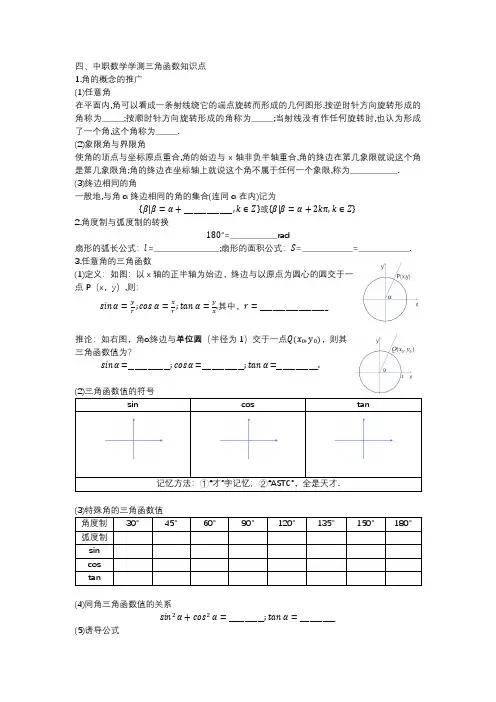
四、中职数学学测三角函数知识点1.角的概念的推广(1)任意角在平面内,角可以看成一条射线绕它的端点旋转而形成的几何图形.按逆时针方向旋转形成的角称为______;按顺时针方向旋转形成的角称为______;当射线没有作任何旋转时,也认为形成了一个角,这个角称为______.(2)象限角与界限角使角的顶点与坐标原点重合,角的始边与x轴非负半轴重合,角的终边在第几象限就说这个角是第几象限角;角的终边在坐标轴上就说这个角不属于任何一个象限,称为_____________. (3)终边相同的角一般地,与角α终边相同的角的集合(连同α在内)记为{ββ|ββ=αα+_______________,kk∈ZZ}或{ββ|ββ=αα+2kkππ,kk∈ZZ}2.角度制与弧度制的转换180°=_____________rad扇形的弧长公式：ll=__________________;扇形的面积公式：SS=______________=______________.3.任意角的三角函数(1)定义：如图：以x轴的正半轴为始边，终边与以原点为圆心的圆交于一点P（x，y）,则：ssss ssαα=yy rr;ccccssαα=xx rr;tt tt ssαα=yy xx.其中，rr=_____________________推论：如右图，角α终边与单位圆（半径为1）交于一点QQ(xx0,yy0)，则其三角函数值为？ssss ssαα=_____________;ccccssαα=_____________;tt tt ssαα=_____________.(2)三角函数值的符号sin cos tan记忆方法：①“才”字记忆；②“ASTC”，全是天才.(3)特殊角的三角函数值角度制30° 45° 60° 90° 120° 135° 150° 180° 弧度制sincostan(4)同角三角函数值的关系ssss ss2αα+ccccss2αα=___________;tt tt ssαα=___________(5)诱导公式公式一公式二公式三ssss ss (2kkππ+αα)= ccccss (2kkππ+αα)= tt tt ss (2kkππ+αα)= ssss ss (−αα)= ccccss (−αα)= tt tt ss (−αα)=ssss ss (ππ+αα)= ccccss (ππ+αα)= tt tt ss (ππ+αα)= 公式四 公式五 公式六ssss ss (ππ−αα)= ccccss (ππ−αα)= tt tt ss (ππ−αα)=ssss ss �ππ2−αα�=ccccss �ππ2−αα�=ssss ss �ππ2+αα�=ccccss �ππ2+αα�=记忆：对全部公式：奇变偶不变，符号看象限； 对一至四：对象作锐角，符号象限找.六、三角函数的图像与性质函数yy =sin xxyy =cos xx五个关键点 xx ∈[0,2ππ] ________、________、________、________、________________、________、________、________、________图像 xx ∈[0,2ππ]定义域 值域 最小正周期奇偶性单调性 在区间_______________________递增； 在区间_______________________递减. 在区间_______________________递增； 在区间_______________________递减. 最值 当x=_____________时，yy mmmmxx =_____. 当x=_____________时，yy mmmm mm =_____. 当x=_____________时，yy mmmmxx =_____. 当x=_____________时，yy mmmm mm =_____. 对称性对称轴为x=_______________________; 对称中心为_______________________.对称轴为x=_______________________; 对称中心为_______________________.。

三角函数一、任意角1. 角的概念的推广 ⑴“旋转”形成角⑵“正角”与“负角”“0角”我们把按逆时针方向旋转所形成的角叫做正角，把按顺时针方向旋转所形成的角叫做负2. “象限角”角的顶点合于坐标原点，角的始边合于x 轴的正半轴，这样一来，角的终边落在第几象限，我们就说这个角是第几象限的角（角的终边落在坐标轴上，则此角不属于任何一个象限） 3. 终边相同的角所有与α终边相同的角连同α在内可以构成一个集合。

{}Z k k S ∈⋅+==,360|οαββ二、弧度制1. 定义：长度等于半径长的弧所对的圆心角称为1弧度的角它的单位是rad ，读做弧度，这种用“弧度”做单位来度量角的制度叫做弧度制．说明：（1）正角的弧度数是正数，负角的弧度数是负数，零角的弧度数是0（2）角α 的弧度数的绝对值公式：lrα= （l 为弧长， r 为半径） 2. 角度制与弧度制的换算：∵ 360︒＝2π rad ∴180︒＝π rad∴ 1︒＝rad rad 01745.0180≈π'185730.571801οοο=≈⎪⎭⎫ ⎝⎛=πrad3. 两个公式1）弧长公式：α⋅=r l 由公式：⇒=r l α α⋅=r l 比公式180rn l π=简单 弧长等于弧所对的圆心角（的弧度数）的绝对值与半径的积 2）扇形面积公式 lR S 21=其中l 是扇形弧长，R 是圆的半径4. 一些特殊角的度数与弧度数的对应值应该记住： 角度 0° 30° 45° 60° 90° 120° 135° 150° 180° 弧度 0π/6π/4π/3π/22π/3 3π/4 5π/6π 角度 210° 225° 240° 270° 300° 315° 330° 360°弧度7π/6 5π/4 4π/3 3π/2 5π/3 7π/411π/62π5. 应确立如下的概念：角的概念推广之后，无论用角度制还是弧度制都能在角的集合与实数的集合之间建立一种一一对应的关系正角 零角 负角正实数 零 负实数任意角的集合 实数集R三、任意角三角函数的定义1. 设α是一个任意角，在α的终边上任取（异于原点的）一点P （x ，y ）则P 与原点的距离02222>+=+=y x yx rry)(x,α（1）把比值r y叫做α的正弦 记作： ry =αsin （2）把比值r x叫做α的余弦 记作： rx =αcos（3）把比值x y叫做α的正切 记作： xy =αtan上述三个比值都不会随P 点在α的终边上的位置的改变而改变.当角α的终边在纵轴上时，即Z)(2∈+=k k ππα时，终边上任意一点P 的横坐标x 都为0，所以tan α无意义；它们都是以角为自变量，以比值为函数值的函数.以上三种函数，统称为三角函数。

中职数学三角函数知识点复习中职数学中的三角函数是数学中的一个重要分支，广泛应用于几何、物理、工程等领域。

三角函数的学习内容较多，本篇文章将对中职数学中的三角函数的基本概念、公式及应用进行复习。

一、基本概念1.弧度制与角度制：弧度制是指以弧长为单位来度量角的大小，而角度制是以度为单位来度量角的大小。

二者之间的转换关系为：1弧度=180°/π；2. 正弦、余弦和正切函数：对于任意角θ，可以定义它的正弦函数sinθ、余弦函数cosθ和正切函数tanθ。

其中，sinθ = 对边/斜边，cosθ = 邻边/斜边，tanθ = 对边/邻边；3.定义域与值域：正弦、余弦和正切函数的定义域为实数集R，值域为[-1,1]；4. 基本关系式：正弦函数与余弦函数的平方和等于1，即sin^2θ + cos^2θ = 1；5.周期性：正弦、余弦和正切函数都具有周期性，其中正弦函数和余弦函数的周期为2π，正切函数的周期为π。

二、基本公式1. 正弦函数的双角公式：sin2θ = 2sinθcosθ；2. 余弦函数的双角公式：cos2θ = cos^2θ - sin^2θ = 1 -2sin^2θ；3. 正切函数的双角公式：tan2θ = 2tanθ/(1 - tan^2θ)；4.正弦函数和余弦函数的和差公式：sin(α ± β) = sinαcosβ ± cosαsinβ；cos(α ± β) = cosαcosβ ∓ sinαsinβ；5.正切函数的和差公式：tan(α ± β) = (tanα ± tanβ)/(1 ∓ tanαtanβ)；6.半角公式：sin(θ/2) = ±√[(1 - cosθ)/2]；cos(θ/2) = ±√[(1 + cosθ)/2]；tan(θ/2) = ±√[(1 - cosθ)/(1 + cosθ)]。

三角函数(1985年——2003年高考试题集)一、选择题 1. t an x ＝1是x ＝45π的 。

(85(2)3分) A.必要条件B.充分条件C.充要条件D.既不充分也不必要条件2. 函数y ＝2sin2xcos2x 是 。

(86(4)3分)A.周期为2π的奇函数 B.周期为2π的偶函数C.周期为4π的奇函数D.周期为4π的偶函数3. 函数y ＝cosx －sin 2x －cos2x ＋417的最小值是 。

(86广东) A.47 B.2C.49D.417 E.4194. 函数y ＝cos 4x －sin 4x 的最小正周期是 。

(88(6)，91(3)3分)A.πB.2πC.2πD.4π5. 要得到函数y ＝sin(2x －3π)的图象，只须将函数y ＝sin2x 的图象 。

(87(6)3分) A.向左平移3π B.向右平移3π C.向左平移6π D.向右平移6π6. 若α是第四象限的角，则π－α是 。

(89上海)A.第一象限的角B.第二象限的角C.第三象限的角D.第四象限的角7. t an 70°＋tan50°－3tan70°tan50°的值是 。

(90广东) A.3B.33C.－33 D.－38. 要得到函数y ＝cos(2x －4π)的图象，只需将函数y ＝sin2x 的图象 。

(89上海) A.向左平移8π个单位 B.向右平移8π个单位 C.向左平移4π个单位 D.向右平移4π个单位9. 函数y ＝cotx|cotx ||tanx |tanx cosx |cosx ||sinx |sinx +++的值域是 。

(90(6)3分)A.{－2，4}B.{－2，0，4}C.{－2，0，2，4}D.{－4，－2，0，4} 10. 若函数y ＝sin(ωx)cos(ωx)(ω＞0)的最小正周期是4π，那么常数ω为 。

(92(2)3)A.4B.2C.21 D.41 注:原考题中无条件“ω＞0”，则当ω取负值时也可能满足条件 11. 在直角三角形中两锐角为A 和B ，则sinAsinB 。

第四章 三角函数第四章 第一课时 角的概念的推广【基础知识·一定要看】1．任意角的概念角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．正角：按____________方向旋转所形成的角．负角：按____________方向旋转所形成的角．零角：如果一条射线没有做任何旋转，我们称它形成了一个零角．2．象限角的判定方法(1)在坐标系中使角的顶点与原点重合，角的始边与x轴的非负半轴重合画出相应的角，观察终边的位置，确定象限．(2)第一步，将α写成α＝k·360°＋β(k∈Z,0°≤β<360°)的形式；第二步，判断β的终边所在的象限；第三步，根据β的终边所在的象限，即可确定α的终边所在的象限，角的终边在第几象限，就说这个角是第几象限角．3．象限角①α是第一象限角可表示为____________________________；(用集合表示)②α是第二象限角可表示为____________________________；③α是第三象限角可表示为____________________________；④α是第四象限角可表示为____________________________．4．非象限角如果角的终边在坐标轴上，就认为这个角不属于任何一个象限．①终边在x轴非负半轴上的角的集合可记作_____________________ ；②终边在x轴非正半轴上的角的集合可记作_____________________；③终边在y轴非负半轴上的角的集合可记作_____________________；④终边在y轴非正半轴上的角的集合可记作_____________________；⑤终边在x轴上的角的集合可记作_____________________；⑥终边在y轴上的角的集合可记作_____________________；5．与角α终边相同的角所有与角α终边相同的角,连同角α在内,可构成一个集合S＝{β|β＝α＋k·360°,k∈Z}.一、选择题1．下列命题正确的是（）．A．终边相同的角是相等的角 B．锐角是小于90°的角C．终边在第二象限的角是钝角 D．相等的角终边重合2．喜洋洋从家步行到学校，一般需要10分钟，则10分钟时间钟表的分针走过的角度是（ ）A．30° B．-30° C．60° D．-60°，那么 的终边在（）3．已知角563A．第一象限 B．第二象限 C．第三象限 D．第四象限4．与20角终边相同的角是（）A．300B．280C．320 D．3405．与75终边相同的角的集合是（），A． 75360,Z k k B． 75360,Z k k C． 180360,Z k k D． (75)360,Z k k 6．已知A {第一象限角}，B {锐角}，C {小于90 的角}，那么A 、B 、C 的关系是（ ） A．B A CB．C C B∪C．A CD．A B C二、填空题7．平面直角坐标系中，若角532α ，则 是第 象限的角. 8．已知2022 ，求与角 终边相同的最小正角为 . 9．在0~180 范围内，与930 终边相同的角是 .二、解答题10．写出与21 终边相同的角的集合S ，并把S 中适合不等式360720 的元素α写出来.11．在0360 范围内，找出与下列各角终边相同的角，并判定它们是第几象限角． （1）150 ； （2）650 .第四章 第二课时 弧度制【基础知识·一定要看】1．弧度制的定义长度等于半径长的圆弧所对的圆心角叫做1弧度角，记作1rad ，或1弧度，或1（单位可以省略不写）． 2．角度与弧度的换算弧度与角度互换公式：180rad1rad =0180≈57．30°=57°18′，1°=180 ≈0．01745（rad ） 3．重要公式弧长公式：___________________，扇形面积公式：___________________．一、选择题1．若角3rad ，则角 是（ ）A．第一象限角B．第二象限角C．第三象限角D．第四象限角2．下列命题中正确的是（ ）．A．1弧度的角就是长为半径的弦所对的圆心角； B．5弧度的角是第三象限角；C． 是第一象限角，则π2也是第一象限角； D．－1弧度角是锐角．3．已知单位圆上有一段长度等于2的弧，则这段弧所对应的圆心角为（ ） A．2B．2C．1D．14．用弧度制表示与150 角的终边相同的角的集合为（ ）A．52,6k k ZB．5180,6k k ZC．22,3k k ZD．52,6k k Z5．若扇形的弧长与面积都是6，则这个扇形的圆心角的弧度数是（ ） A．2B．3C．4D．56．圆的半径变为原来的2倍，而弧长也增加到原来的2倍，则（ ） A．扇形的圆心角大小不变B．扇形的圆心角增大到原来的2倍 C．扇形的圆心角增大到原来的4倍D．不能确定7．某学校大门口有一座钟楼，每到夜晚灯光亮起都是一道靓丽的风景，有一天因停电导致钟表慢10分钟，则将钟表拨快到准确时间分针所转过的弧度数是（ ） A．3B．6C．6D．3二、填空题8．将–1485°化为2kπ+α（0≤α<2π，k ∈Z ）的形式是 . 9．与240 终边相同的所有角的集合用弧度制可以表示为 . 10．弧长为3 ，圆心角为135 的扇形，其面积为 . 11．用弧度制表示终边落在第二象限的角的集合为 .三、解答题12．已知一个扇形的面积为4，周长为10，求该扇形的半径和圆心角． 13．用弧度制写出终边在阴影部分的角的集合：（1） （2）第四章 第三课时 任意角的三角函数【基础知识·一定要看】1．三角函数定义设 是一个任意角，它的终边与半径是r 的圆交于点(,)P x y ，则r ，那么： （1）y r 做 的正弦，记做sin ，即sin y r ； （2）x r 叫做 的余弦，记做cos ，即cos x r ；（3）y x 叫做 的正切，记做tan ，即tan (0)yx x ．2．三角函数在各象限的符号在记忆上述三角函数值在各象限的符号时，有以下口诀：（全是天才）． 判断三角函数值在各象限符号的攻略：1 基础：准确确定三角函数值中各角所在象限；2 关键：准确记忆三角函数在各象限的符号；3 注意：用弧度制给出的角常常不写单位，不要误认为角度导致象限判断错误. 3．正弦、余弦、正切函数的定义域一、选择题1．已知角 的终边经过点(8,6)，则cos 的值为（ ）A．34 B．43C．45 D．352．若sin 0,cos 0 ，则 是（ ）A．第一象限角B．第二象限角C．第三象限角D．第四象限角3．若点(1,2)P 在角 的终边上，则sin （ ）A．2B．12C．54．若角 的终边经过点(2,3)P ，则tan 等于（ ） A．23B．32C．32D．235．已知角 在第二象限，则（ ）A．sin 0 ，cos 0 B．sin 0 ，cos 0 C．sin 0 ，cos 0D．sin 0 ，cos 06．已知角 的终边经过(1,3) ，则cos sin （ ）C．D．7．如果角 的终边经过点(3,2) ，则sin 2cos 3sin cos（ ）A．－49B．49C．111D．－1118．已知角 的顶点与原点重合，始边与x 轴非负半轴重合，若 1,A y 是角 终边上一点，且sin y （ ） A．3B．3C．1 D．19．已知角 的终边经过点 3,4P ，则sin cos 11tan的值为（ ）A．65B．1 C．2 D．310．已知角 的顶点与原点 重合，始边与x 轴的非负半轴重合，终边过点(),40P m m ，且cos 5m，则tan （ ） A．43B．43 C．34D．34二、填空题11．已知角 的终边上有一点(1,3) ，则sin . 12．若角 的终边过点 3,4 ，则cos sin .13．确定下列各式的符号：sin105cos 230 0（填“ ”、“ ”或“ ”）. 14．已知sin tan 0 ，则角 位于第 象限．三、解答题15．已知角 的终边经过点(,6)P x ，且5cos 13，求x 的值.16．已知角 的终边上一点P 的坐标为 4,3t t （其中0t ），求角 的正弦、余弦和正切值．17．已知角 的顶点与坐标原点O 重合，始边落在x 轴的正半轴上，终边经过点04,A y ，其中00y .（1）若cos 5，求0y 的值； （2）若04y ，求2sin 3cos cos 4sin的值.第四章 第四课时 同角三角函数的基本关系【基础知识·一定要看】1．同角三角函数的基本关系式 （1）平方关系：_______________；（2）商数关系：_______________ 2．利用同角三角函数的基本关系常见题型： 1 知一求二 2 弦切转换3．sin α＋cos α，sin α－cos α，sin αcos α三个式子中，已知其中一个，可以求其他两个，即“知一求二”，它们之间的关系是：(sin α±cos α)2＝1±2sin αcos α. 4．特殊角的三角函数值1．若sin ， 为第四象限角，则cos 的值为（ ）A．2B．12C．2D．122．已知5cos 13，且 为第二象限角，则tan （ ） A．125B．512C．1213 D．13123．已知tan 2 ,则cos sin sin cos的值为（ ）A．13B．13 C．3 D．34．已知 是第二象限角，tan 2 ，则cos 等于（ ）A．5B．15 C．5D．255．已知 的值为（ ） A．sin B．sin C．sin D．cos6．已知角 的顶点与原点重合，始边与x 轴的正半轴重合，点(1,3)P 在角 的终边上，则sin cos 2sin 3cos（ ）A．34 B．34 C．49D．497．已知tan 2 ，则2sin 2sin cos 的值为（ ）A．85B．1 C．0D．858．若π(0,)2 ，212tan cos，则tan （ ）A．12B．1C．2 9．已知sin cos 3sin cos ，22，则sin cos （ ）A．B． 10．已知10,sin cos 25 ，则221cos sin的值为（ ）A．75 B．257C．725 D．2425二、填空题11．已知3sin 5 ，,2，则cos . 12．若4cos 5，则sin . 13．若 为第二象限角，且1sin 3，则tan ＝ .14．已知7sin cos 13，(0,) ，则sin cos = .15．若sin 2cos 0A A ，则2sin cos sin 3cos A AA A. 16．已知角 的始边为x 轴非负半轴，终边经过点P （1，2），则sin sin cos.17．已知1sin cos 3，则44sin cos .18．已知1sin cos (0π)5，则tan .二、解答题19．已知1sin 5，并且 是第二象限角，求cos ，tan 的值；20．已知 为第二象限角，且4sin 3cos 0 ． （1）求tan 与sin 的值； （2）sin 2cos 2sin cos的值．第四章 第五课时 诱导公式【基础知识·一定要看】 1．诱导公式 诱导公式一：sin(2)sin k ； cos(2)cos k ； tan(2)tan k ，其中k Z诱导公式二：sin()sin ； cos()cos ； tan()tan ，其中k Z诱导公式三：sin[((21)]sin k ； cos[(21)]cos k ； tan[(21)]tan k ，其中k Z 诱导公式四：sin cos 2 ； cos sin 2 ； sin cos 2 ； cos sin 2，其中k Z一句话：对象当锐角，符号象限找一、选择题1． cos 300 （ ）A．12B．12C．2D． 2．如果12sin 13 ，02，，那么 cos （ ） A．1213 B．513C．1213D．5133．若tan (π)3 ，则2cos sin cos （ ）A．25B．35C．35D．25三、填空题4．已知sin 2sin() 的值是 . 5．15cos 4. 6．计算22sin ()cos () . 7．化简下列各式（1） cos ；（2） sin ；（3） tan .8．已知角 的终边经过点(2,1)P ，则cos 2的值为 .9．若 1cos 2π3，则 sin 3 .三、解答题10．求下列角的三角函数值： （1）cos(1050 )（2）sin(314)11．已知角 的终边经过点 3,40P a a a ． （1）求sin 的值；（2）求 3sin cos 2的值．12．已知2 ，3sin 5. （1）求tan 的值；（2）求 sin 2cos 2sin cos的值．22．已知sin 3sin 232cos cos 2f. （1）化简 f .（2）已知tan 3 ，求 f 的值.第四章 第六课时 正弦函数的图像和性质【基础知识·一定要看】1．“五点法”作y ＝sin x 的图像在确定正弦函数y ＝sin x 在[0，2π]上的图象形状时，起关键作用的五个点是： ______________________________________________．2．正弦函数的性质1．用五点法画y ＝sin x ，x ∈[0,2π]的图像时，下列哪个点不是关键点（ ） A．1,62B．,12C．(π，0) D．(2π，0)2．函数sin ,[0,2]y x x 与12y 图像交点的个数为（ ） A．0B．1C．2D．33．正弦函数y ＝sin x ，x ∈R 的图象的一条对称轴是（ ） A．y 轴B．x 轴C．直线x＝2D．直线x＝π4．函数()2sin f x x 在区间3π0,4上的最大值为（ ）A．0 B． D．2 5．已知集合 sin ,M y y x x R ， 12N x x ，则M N （ ） A． 1,1 B． 1,2C． 1,1 D． 1,16．函数y ＝|sin x |的图象( )A．关于x 轴对称B．关于y 轴对称C．关于原点对称 D．关于坐标轴对称 7．在同一坐标系中函数y ＝sin x ，x ∈[0，2π]与y ＝sin x ，x ∈[2π，4π]的图象( )A．重合B．形状相同，位置不同 C．形状不同，位置相同 D．形状不同，位置不同8．满足1sin 2的角的集合为（ ） A．2,3k kZB．2,6k kZC．222,33k k kZ D．522,66k k kZ 二、填空题9．函数 2sin f x x 的最大值是 . 10．函数3sin 2y x 的最小值为 .11．函数4sin 3y x 在[,] 上的递增区间为 . 12．观察正弦函数的图像，可得不等1sin 2x的解集为 . 13．已知函数 sin 1f x a x bx ，若 12f ，则 1f .三、解答题19．设2sin 4x m ，x R ，求m 的取值范围.20．已知函数()sin 2f x x .（1）求函数()f x 的最小正周期；（2）当x [0,2π]时，求函数()f x 的最大值及取得最大值时x 的值.22．写出函数3sin 1y x 的值域和单调区间.第四章 第七课时 余弦函数的图像和性质【基础知识·一定要看】1．“五点法”作y ＝cos x 图像在确定余弦函数y ＝cos x 在[0，2π]上的图象形状时，起关键作用的五个点是 ______________________________________________．2．余弦函数的性质1．已知点5(,)6m在余弦曲线上，则m ＝（ ） A．2B．－2C．12D．－122．已知m 是函数 cos f x x 图象一个对称中心的横坐标，则 f m （ ） A．1B．0C．12D．13．从函数 cos ,0,2y x x 的图象来看，当 0,2x 时，对于cos x 的x 有（ ） A．0个B．1个C．2个D．3个4．在区间0,2上，下列说法正确的是（ ）A．sin y x 是增函数，且cosy x 是减函数 B．sin y x 是减函数，且cos y x 是增函数 C．sin y x 是增函数，且cos y x 是增函数 D．sin y x 是减函数，且cos y x 是减函数 5．函数cos y x 的一个单调递增区间是（ ）A． ,22B．[0，π] C．[π，32 ] D．[32 ，2π]6．函数cos y x 在区间[ ，a ]上为增函数，则a 的取值范围是（ ）A．(,)2B．( ，0] C．(2，0]D．(,)二、填空题7．若cos 21x m ，且R m ，则m 的取值范围是 ． 8．函数cos y x 相邻对称中心之间距离为 ． 9．函数 2cos 2cos 1f x x x 的最小值是 ．10．函数5()cos ,,46ππf x x x的值域为 ．三、解答题11．已知函数cos y a x b 的最大值是0，最小值是4 ，求,a b 的值．12．求使函数1cos 12y x 取得最大值，最小值的自变量x 的取值范围，并分别写出最大值，最小值.。

中职数学三角函数教案一、教学目标1、理解正弦、余弦、正切等函数的定义和性质。

2、掌握三角函数的恒等变换和图像绘制。

3、能够利用三角函数解决实际问题，如测量、工程、物理等问题。

4、培养学生的数学思维和解决问题的能力。

二、教学内容1、三角函数的定义和性质2、三角函数的恒等变换3、三角函数的图像绘制和应用实例三、教学难点与重点难点：理解三角函数的恒等变换和应用实例的解决。

重点：掌握三角函数的定义和性质，以及三角函数的图像绘制。

四、教具和多媒体资源1、黑板和粉笔。

2、投影仪和PPT。

3、教学软件：GeoGebra或Desmos图形计算器。

五、教学方法1、激活学生的前知：复习初中所学的锐角三角函数。

2、教学策略：讲解、示范、小组讨论、案例分析。

3、学生活动：小组讨论、绘制函数图像、解决实际问题。

六、教学过程1、导入：故事导入，以实际应用案例引入三角函数的概念。

2、讲授新课：通过讲解、示范和PPT展示，引导学生理解三角函数的定义和性质，掌握恒等变换的运用，并能够绘制三角函数的图像。

3、巩固练习：提供几个实际应用案例，让学生利用所学知识解决，加深对三角函数的理解和应用。

4、归纳小结：回顾本节课的重点和难点，总结三角函数的基本概念、性质和恒等变换的应用。

七、评价与反馈1、设计评价策略：测试、小组讨论、观察学生的表现。

2、为学生提供反馈，针对不同学生给出具体的建议和指导，以便学生更好地掌握所学内容。

八、作业布置1、完成教材上的练习题。

2、自己寻找一个实际应用案例，写出解决方案并绘制出相关的图像。

中职数学三角函数试卷一、选择题1、以下哪个是三角函数？（）A.正弦B.余弦C.正切D.以上都是2、三角函数的定义域是什么？（）A.实数集B.有理数集C.正实数集D.单位圆上的点3、下列哪个选项的三角函数值为正？（）A. sin(0)B. cos(π/2)C. tan(π/4)D.以上都是二、填空题4、写出下列角度的正弦、余弦和正切值（精确到小数点后两位）：角度1：30度；角度2：45度；角度3：60度；角度4：90度；角度5：180度。

中职三角函数的概念教案三角函数是数学中的一种重要的函数类别，它是研究角度和边长之间的关系的数学工具。

在中职阶段，三角函数的学习是为了理解和应用几何图形中的角度和边长的关系，以及在实际问题中的应用。

一、三角函数的基本概念三角函数包括正弦函数、余弦函数和正切函数。

在右边的图中，我们可以看到一个任意给定角度θ（大写希腊字母Theta）。

其中，a、b和c分别表示一个直角三角形的边长，其中的角度θ位于竖直边a和斜边c之间。

这里，我们需要理解以下关系：1. 正弦函数（sine）：表示a和c之间的比值，即sin(θ) = a/c。

2. 余弦函数（cosine）：表示b和c之间的比值，即cos(θ) = b/c。

3. 正切函数（tangent）：表示a和b之间的比值，即tan(θ) = a/b。

这三个函数在三角形的不同位置上取值，而取值范围是在-1到1之间。

当角度θ变化时，这三个函数的值也会随之变化。

二、三角函数的图像和性质1. 正弦函数的图像：正弦函数的图像是一个周期函数，它在一个周期2π内，从0到2π的范围内以曲线形式循环变化。

在x轴上的原点，即角度为0时，正弦函数的值为0。

正弦函数图像关于y轴对称，并且在每个周期内都是偶函数。

即sin(-θ) = -sin(θ)，其中θ为任意角度。

2. 余弦函数的图像：余弦函数的图像也是一个周期函数，它与正弦函数的图像非常相似。

不同之处在于余弦函数在x轴的原点，即角度为0时，余弦函数的值为1。

余弦函数图像关于y轴对称，并且在每个周期内都是偶函数。

即cos(-θ) = cos(θ)，其中θ为任意角度。

3. 正切函数的图像：正切函数的图像是一个周期函数，它的周期是π。

在x轴的原点，即角度为0时，正切函数的值为0。

正切函数的图像关于原点对称，在每个周期内都是奇函数。

即tan(-θ) = -tan(θ)，其中θ为任意角度。

三、三角函数的应用三角函数在实际问题中有着广泛的应用，以下介绍一些常见的应用场景：1. 几何图形的测量与解析：在几何图形的测量与解析中，三角函数可以帮助我们计算角度、边长和面积。