下载文档原格式
xn=a2un的z变换及收敛域首先，我们来讨论xn=a^2un的z变换。
Z变换是一种离散时间信号的频域表示方法，它将离散时间序列xn映射到复平面上的函数X(z)。
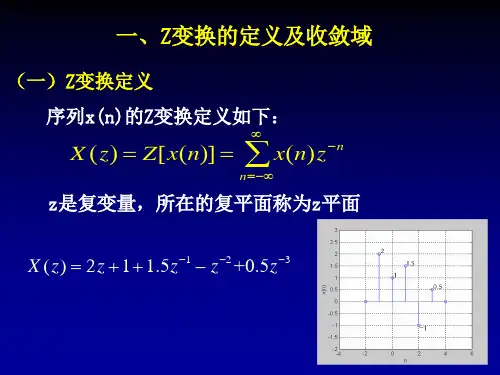
对于给定的离散时间序列xn，其z变换X(z)定义如下：X(z) = Z{xn} = Σ(xn z^(-n))。
其中，n取遍所有整数，z为复变量。
现在我们来计算xn=a^2un的z变换。
根据定义，我们有：X(z) = Z{a^2un} = Σ((a^2un) z^(-n))。
由于un是单位阶跃函数，它的定义如下：un = 1, n >= 0。
un = 0, n < 0。
因此，我们可以将上述求和分为两个部分来计算：X(z) = Σ((a^2 1) z^(-n)), n >= 0。
= Σ(0 z^(-n)), n < 0。
对于第一个部分，我们可以将a^2提取出来，得到： X(z) = a^2 Σ(z^(-n)), n >= 0。
这是一个等比级数求和，其求和公式为：Σ(z^(-n)) = 1 / (1 z^(-1))。
将其代入上式，我们得到：X(z) = a^2 (1 / (1 z^(-1))), n >= 0。
对于第二个部分，我们有：X(z) = Σ(0 z^(-n)), n < 0。
= 0。
综上所述，xn=a^2un的z变换为：X(z) = a^2 (1 / (1 z^(-1))), n >= 0。
= 0, n < 0。
接下来我们来讨论收敛域。
收敛域是指在复平面上，z变换X(z)收敛的区域。
对于上述的X(z) = a^2 (1 / (1 z^(-1)))，它在什么区域内收敛呢？我们知道，收敛域取决于级数的绝对值是否收敛。
对于上述的X(z)，当|z| > 1时，级数1 / (1 z^(-1))绝对值不收敛，因此X(z)在|z| > 1的区域内不收敛。
当|z| < 1时，级数1 / (1 z^(-1))绝对值收敛，因此X(z)在|z| < 1的区域内收敛。
