z变换的收敛域
- 格式:ppt
- 大小:494.51 KB
- 文档页数:16


1.举例说明什么是因果序列和逆因果序列,并分别说明它们z 变换的收敛域。
答:因果序列定义为x (n )=0,n<0,例如x (n )=)(n u a n ⋅,其z 变换收敛域:∞≤<-z R x 。
逆因果序列的定义为x (n)=0,n>0。
例如x (n )=()1--n u a n ,其z 变换收敛域:+<≤x R z 02.用差分方程说明什么是IIR 和FIR 数字滤波器,它们各有什么特性? 答: 1)冲激响应h (n )无限长的系统称为IIR 数字滤波器,例如()()()1)(21)(1021-++-+-=n x b n x b n y a n y a n y 。
IIR DF 的主要特性:①冲激响应h (n )无限长;②具有反馈支路,存在稳定性问题;③系统函数是一个有理分式,具有极点和零点;④一般为非线性相位。
(2)冲激响应有限长的系统称为FIR DF 。
例如()2)1()()(21-+-+=n x b n x b n x n y 。
其主要特性:①冲激响应有限长;②无反馈支路,不存在稳定性问题;③系统函数为一个多项式,只存在零点;④具有线性相位。
3.用数学式子说明有限长序列x (n )的z 变换X (z )与其傅里叶变换X )(ωj e 的关系,其DFT 系数X (k )与X (z )的关系。
答: (1)x (n )的z 变与傅里叶变换的关系为()()ωωj e Z e X z X j== (2)x (n )的DFT 与其z 变换的关系为()()K X z X k N j K N e w Z ===- 2 π4.设x (n )为有限长实序列,其DFT 系数X (k )的模)(k X 和幅角arg[X (k )]各有什么特点?答:有限长实序列x (n )的DFT 之模()k x 和幅角[])(arg k X 具有如下的性质:(1))(k X 在0-2π之间具有偶对称性质,即)()(k N X k X -=(2)[])(arg k x 具有奇对称性质,即[]()[]k N X k X --=arg )(arg5.欲使一个FIR 数字滤波器具有线性相位,其单位取样响应)(n h 应具有什么特性?具有线性相位的FIR 数字滤器系统函数的零点在复平面的分布具有什么特点?答: 要使用FIR 具有线性相位,其h (n )应具有偶对称或奇对称性质,即h(n)=h(N-n-1)或h(n)=-h(N-n-1)。

z变换收敛域z变换收敛域是一种数字图像处理中应用非常广泛的技术。
它是一种快速而有效的方法,可以转换图像中的信号,从而实现对图像进行处理。
z变换收敛域也称为变换收敛域(TFD),它是从z变换出发的一种重要概念。
z变换收敛域是将一个时域信号转换成频域的一种方法,它能够将时域信号的特性转换到频域,从而使得处理者可以更好地理解信号的特性,而不用去考虑其时间特性。
z变换收敛域也可以被用来分析信号的频率响应特性,以及信号的振幅和相位响应特性。
z变换收敛域能够帮助我们了解信号的细节,并更好地掌握信号的特性。
z变换收敛域的定义如下:当一个时域信号作用于z 变换之后,即[Z (n)] = [F (n)] X [H (z)],其中[F (n)] 是信号的时域表达式,[H (z)] 是信号的z变换表达式,则[Z (n)] 的收敛域就是所有可能的[F (n)] 和[H (z)] 的组合,它们能够使[Z (n)] 收敛到有界值∞。
z变换收敛域也可以看作是一种“传递函数”,它可以描述信号在每一个时刻都是如何传播的,和信号受到外部影响时会有什么样的变化。
z变换收敛域的传递函数可以用来描述信号的延迟、增益、衰减、抑制等特性,从而帮助我们更好地理解信号的特性。
z变换收敛域的收敛域是一个多元函数,它由一个或多个维度组成,每个维度都代表一种特定的属性,例如,收敛域的一维可以表示信号在不同频率上的振幅响应,收敛域的二维可以表示信号在不同频率上的相位响应,三维可以表示信号在不同频率上的衰减响应等等。
z变换收敛域的应用非常广泛,它能够帮助我们更好地理解信号的特性,并帮助我们更好地处理信号。
它能够检测和分析信号的特性,并且能够提供信号的实时反馈和诊断,从而为信号的处理和控制提供依据,以及帮助我们更好地处理和控制信号。
此外,z变换收敛域还可以用来检测和控制信号的相位和频率响应,以及检测和控制信号的延迟、衰减和抑制等特性。
总之,z变换收敛域是一种非常有效的技术,它可以帮助我们更好地理解信号的特性,并且能够提供有效的信号处理和控制的依据,从而使我们能够更好地处理信号。




z变换的收敛域
z变换的收敛域是指在哪些复平面上的z值,使得z变换的级数或积分收敛。
z变换的收敛域通常按照其包含在复平面第一象限
(Re(z)>0,Im(z)>0)还是全平面(包括虚轴)来分类,分别称为单边收敛和双边收敛。
对于时域信号x(n)的z变换X(z),其收敛域的判断方法为:
1.通过分析x(n)的极限,确定z变换的极点和零点,并求出其可能的收敛域。
2.通过柯西收敛原理,判断z变换的收敛域。
3.对于一些标准的信号,比如因果序列、双边指数信号等,可以直接列出其z变换并判断收敛域。
在工程应用中,通常只需关注z变换的最小收敛域,即最小包含其所有极点的收敛域。
最小收敛域也称为“ROC”,表示因果性和稳定性的限制条件。



1.举例说明什么是因果序列和逆因果序列,并分别说明它们z 变换的收敛域。
答:因果序列定义为(n )=0,n<0,例如(n )=,其z 变换收x x )(n u a n ⋅敛域:。
逆因果序列的定义为(n)=0,n>0。
例如(n )=∞≤<-z R x x x ,其z 变换收敛域:()1--n u a n +<≤x R z 02.用差分方程说明什么是IIR 和FIR 数字滤波器,它们各有什么特性? 答:1)冲激响应h (n )无限长的系统称为IIR 数字滤波器,例如。
()()()1)(21)(1021-++-+-=n x b n x b n y a n y a n y IIR DF 的主要特性:①冲激响应h (n )无限长;②具有反馈支路,存在稳定性问题;③系统函数是一个有理分式,具有极点和零点;④一般为非线性相位。
(2)冲激响应有限长的系统称为FIRDF 。
例如。
()2)1()()(21-+-+=n x b n x b n x n y 其主要特性:①冲激响应有限长;②无反馈支路,不存在稳定性问题;③系统函数为一个多项式,只存在零点;④具有线性相位。
3.用数学式子说明有限长序列(n )的z 变换X (z )与其傅里叶变换X x 的关系,其DFT 系数X (k )与X (z )的关系。
)(ωj e 答: (1)(n )的z 变与傅里叶变换的关系为x ()()ωωj e Z e X z X j == (2)(n )的DFT 与其z 变换的关系为x ()()K X z X k Nj K New Z ===- 2 π4.设(n )为有限长实序列,其DFT 系数X (k )的模和幅角arg[X (k )]各x )(k X 有什么特点?答:有限长实序列(n )的DFT 之模和幅角具有如下的性质:x ()k x [])(arg k X (1)在0-2之间具有偶对称性质,即)(k X π)()(k N X k X -=(2)具有奇对称性质,即[])(arg k x []()[]k N X k X --=arg )(arg 5.欲使一个FIR 数字滤波器具有线性相位,其单位取样响应应具有什么特)(n h 性?具有线性相位的FIR 数字滤器系统函数的零点在复平面的分布具有什么特点?答: 要使用FIR 具有线性相位,其h (n )应具有偶对称或奇对称性质,即h(n)=h(N-n-1)或h(n)=-h(N-n-1)。
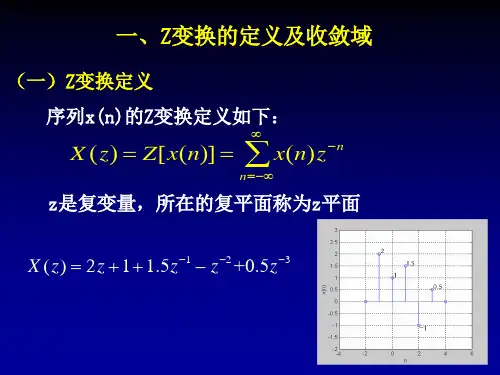
2. Z 变换的定义及收敛域1. Z变换的定义对于一个序列x(n),它的Z 变换定义为()()n n X z x n z ∞-=-∞=∑其中Z 为一个复变量,上式定义的Z 变换称为双边Z 变换或标准Z 变换。
序列的Z 变换实质上是以序列x(n)为加权系数的z 的幂级数之和。
如n 的取值范围0到+∞,则序列的单边Z 变换为()()nn X z x n z∞-=-∞=∑序列的单边Z 变换是以序列x(n)为加权系数的z 的负幂项的级数之和。
2.从抽样吸纳后的拉普拉斯变化引出Z 变换 连续信号x(t)冲激抽样信号可表示为:()()()s s s n x nT x t t nT δ∞=-∞=-∑()()s s nx nT t nT δ=-∑对()s s x nT 取拉普拉斯变换,得()()sts s X s x nT e dt ∞--∞=⎰()()sts s nx nT t nT e dt δ∞--∞=-∑⎰()()s s snT sT s n x nT e X e ∞-=-∞==∑令s sT z e =,并将T 归一化为1,()s x nT 简写为()x n 则同样可得到离散信号的 z 变换:()()nn X z x n z∞-=-∞=∑对比: 拉普拉斯变换 Z 变换 对应离散信号,s j σ=+Ω(2f πΩ=是相对连续系统和连续信号的角频率) 则()s s s s sT j T T j T z e e e e σσ+ΩΩ===⋅, 令,s T r e σ=, 2s s T f f ωπ=Ω=是相对于离散系统和离散信号的圆周频率(rad ), 则j z re ω=。
将j z re ω=代入()()nn X z x n z∞-=-∞=∑可得:()()()j nn X z x n reω∞-=-∞=∑=[()]nj n n x n re ω∞--=-∞∑上式表明,只要()nx n r -满足绝对可和的收敛条件,即()n n x n r ∞-=-∞<∞∑,则x(n)的Z 变换存在。