比、比例和百分比

小学数学比例的知识点在小学数学的学习中，比例是一个非常重要的概念。

比例是数学中常见的关系表示方法，它可以帮助我们理解和计算各种数量之间的比较关系。

本文将介绍小学数学比例的基本知识点，包括比例的定义、比例的性质以及比例的应用。

一、比例的定义比例是指两个或多个数量之间的相对关系。

比例通常以等式形式表示，用两个冒号“:”或者一个分数线“/”来表示比例关系。

例如：1:2、1/2。

比例的定义可以进一步扩展为三个要素：比例的前项、比例的后项以及比例的比值。

其中，比例的前项是指被比较的较小的数量，比例的后项是指被比较的较大的数量，比例的比值是指前项和后项之间的比值关系。

二、比例的性质比例具有一些重要的性质，理解这些性质能够帮助我们更好地应用比例进行计算。

1. 交换律：比例中的前项与后项交换位置后，比值不变。

例如，1:2和2:1表示的比例是相等的。

2. 乘法律：比例中的前项（或后项）同时乘以一个数，比例的比值也相应乘以相同的数。

例如，1:2乘以2，得到2:4，仍然表示相等的比例关系。

3. 倍数律：比例中的前项（或后项）变成原来的倍数，比例的比值也相应变成原来的倍数。

例如，1:2变成2:4，表示的仍然是相等的比例关系。

三、比例的应用比例在日常生活和数学问题中有着广泛的应用。

1. 比例的放缩：根据已知比例关系，可以计算出未知数量的值。

例如，如果知道一辆车以60公里/小时的速度行驶了3小时，就可以利用比例关系来计算该车行驶的距离。

2. 比例的类比：比例关系可以帮助我们理解和解决各种问题，如图形的相似、物体的估算等。

比例关系可以将一个问题与另一个类似的问题相联系，从而简化解决的过程。

3. 百分比：百分比是一种特殊的比例关系，通常以百分号“%”来表示。

百分比可以帮助我们将一个数值表示为另一个数值的多少部分。

例如，考试成绩的百分比可以反映出一个学生在某一科目中所占的相对成绩。

总结：比例是小学数学中的重要知识点，它可以帮助我们理解和计算各种数量之间的比较关系。

学科教师辅导讲义
运用比的基本性质，可以化简比
最简整数比：最简整数比是指比的前项和后项都是整数，且它们互素 （3）连比以及三连比的性质
（1）如果 k n m c b a k n c b n m b a ::::,::,::===那么 （2）如果k
c k b k a ck bk ak c b a k ::::::,0=
=≠那么 3.比例的意义：表示两个比相等的式子叫比例．
组成比例的四个数都不能是0． （1） 比例的基本性质
在比例中，两个内项和乘积，等于两个外项的乘积 例如：180∶3=240∶4 两个内项相乘：3×240=720 两个外项相乘：180×4=720
这两个乘积有相等的关系，如果把比例写成分数形式，等号两端的分子和分母分别交叉相乘，积也有这种关系，
（2） 如何判断两个比能否成比例
根据比例的意义和性质可以判断两个比能否组成比例
（3）解比例
求比例中的未知数叫做解比例
根据比例的基本性质，可以解比例
解比例后，检查是否正确的几种方法
①将x值代入原比例式中，看两个比的比值是否相等，比值相等，说明计算正确．
②将x值代入比例式中，看两个外项积是否等于两个内项积，如果两个积相等，说明计算准确．
③将x值代入原比例式中，写成分数形式，然后两个分数相除，商是否等于1，如果商是1，说明计算准确．
4. 比和比例的联系与区别
比和比例既有联系，又有区别
联系：比和比例有密切的联系，比例是由两个相等的比组成的，如果两个比相等，那么这两个比就可以组成比例，成比例的两个比，比值一定相等．例如
区别：比表示两个数相除，有两项：
比例是一个等式，表示两个比相等，有四项．
5. 求比值和化简比。

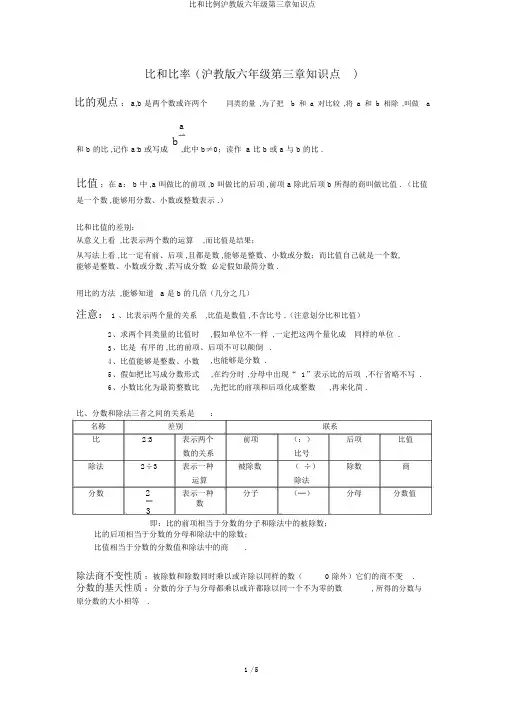
比和比率 ( 沪教版六年级第三章知识点)比的观点： a,b 是两个数或许两个同类的量,为了把b和a对比较,将a和b相除,叫做aa和 b 的比 ,记作 a:b 或写成b,此中 b≠0；读作 a 比 b 或 a 与 b 的比 .比值：在 a： b 中 ,a 叫做比的前项 ,b 叫做比的后项 ,前项 a 除此后项 b 所得的商叫做比值 . （比值是一个数 ,能够用分数、小数或整数表示 .）比和比值的差别：从意义上看 ,比表示两个数的运算,而比值是结果；从写法上看 ,比一定有前、后项 ,且都是数 ,能够是整数、小数或分数；而比值自己就是一个数,能够是整数、小数或分数 ,若写成分数必定假如最简分数 .用比的方法 ,能够知道 a 是 b 的几倍（几分之几）注意： 1 、比表示两个量的关系,比值是数值 ,不含比号 .（注意划分比和比值）2、求两个同类量的比值时,假如单位不一样 ,一定把这两个量化成同样的单位 .3、比是有序的 ,比的前项、后项不可以颠倒 .4、比值能够是整数、小数,也能够是分数 .5、假如把比写成分数形式,在约分时 ,分母中出现“ 1”表示比的后项 ,不行省略不写 .6、小数比化为最简整数比,先把比的前项和后项化成整数,再来化简 .比、分数和除法三者之间的关系是：名称差别联系比2:3表示两个前项（：）后项比值数的关系比号除法2÷3表示一种被除数（÷）除数商运算除法分数2表示一种分子（─）分母分数值3数即：比的前项相当于分数的分子和除法中的被除数；比的后项相当于分数的分母和除法中的除数；比值相当于分数的分数值和除法中的商.除法商不变性质：被除数和除数同时乘以或许除以同样的数（0 除外）它们的商不变.分数的基天性质：分数的分子与分母都乘以或许都除以同一个不为零的数, 所得的分数与原分数的大小相等.比的基天性质： 比的前项和后项同时乘以或许除以同样的数（0 除外） ,比值不变 .能够化为最简整数比 .注意：1、整数比的化简就是用比的前项和后项同时除以它们的最大公因数 ,直至两个前项和后项互素；2、分数比的化简能够把比式当作除式 ,直接进行分数除法运算（假如用除法化简的结果是整数 ,那么分母 1 不可以省略 ,把商化成比的形式）；3、小数比的化简先把比的前项和后项化成整数 ,再来化简；4、带有单位的比的化简 ,先把单位一致后在化简.最简整数比 是指比的前项与后项都是整数且它们互素.（比中的各数除了 1 以外 ,没有其他的公因数 ,这样的比称为最简整数比.）在化最简整数比时 ,若比的各项都是整数 ,只要每项除以各项的最大公因数 , 即化为最简整数比；若比项中出现分数（或小数） ,那么先化成整数比 ,在除以各项的最大公因数 .三项连比的性质1、假如 a ： b=m ： n ；b ： c=n ：k, 那么 a ： b ：c=m ： n ： ka b c2、假如 k ≠0,那么 a ： b ： c=ak ： bk ： ck= k ： k ：k注意： 1 、三个数（或多个数）的比也是有序的.2 、一般的 ,假如 a ： b=m ：n,b ： c=p ： q,（此中 n ≠0,p ≠0,q ≠0,n,p 互素） ,那么连比a ：b ： c=mp ：np ： nq 在求三个数的连比时,就是要把两个比中同样字母所对应的项上的数化成同样的数,而后再写出连比的形式 .写连比时要注意三个数字的前后次序 .比率尺 =图上距离：实质距离比率比率： a 、b 、 c 、d 四个量中 ,假如 a ： b=c ： d,那么就说a 、b 、c 、d 成比率 ,也就是表示两个比相等的式子叫做比率 .（此中 a、b 、 c、 d 分别叫做第一、二、三、四比率项 ,第一比率项 a 和第四比率项 d 叫做比率外项；第二比率项 b 和第三比率项 c 叫做比率内项 .）假如两个比率内项同样,即 a ： b=b ： c,那么把 b 叫做 a 和 c 的比率中项 .比率的基天性质：（内项之积等于外项之积）a c即 ,假如 a ：b=c ： d 或b d,那么 ad=bc, 反之 ,假如 a、 b 、 c、 d 都不为零 ,且 ad=bc, 那么a ca ： b=c ： d 或bd .a c比率的基天性质可进行比率变形,常用的变形有：b da b互换两内项得：c d1、d c互换两外项得：b a2、d b同时互换两个内、外项得：c a3、百分比n百分比：把两个数目的比值写成100的形式,称为百分数,也叫做百分比或百分率,记作20n%, 读作百分之n.符号“ % ” ,叫做百分号 .比如 20% 就是100,读作百分之二十.百分数是一种特别的倍数关系,一个特别的比,它的后项是一个固定的数100, 所以又称为百分率或百分比.因为百分数是分母为100 的特别分数 ,既能直观的反应部分与整体的关系,又便于比较 ,所以在工农业生产和生活中运用比较宽泛.分数既能够表示一个数,也能够表示两个数的比；百分数只好表示两个数的比,后边不可以带单位名称 .小数化成百分数：小数化成百分数,将小数点向右移两位,同时在右边增添百分号.3 / 5百分数化成小数：将百分号前的数字的小数点向左移两位,同时去掉后边的百分号.（分数化成小数不可以除尽用“≈” ,小数化成百分数用“=” .）百分比的实质应用及格人数及格率100总人数％合格产品数合格率100产品总数％增添的产量增产率100本来的产量％实质出勤人数出勤率100应当出勤人数％得票数得票率100总的投票数％增添的数增添率100本来的基数％盈余100售价 -成本100盈余率成本成本％ =％损失100成本 -售价100损失率成本成本％ =％恩格尔系数食品花费支出总数100花费支出总数％一个百分点相当于1%, 它是剖析百分比增减改动的一种表现形式.九五折就是原价的95%一成相当于10%利息 =本金×利率×期数等可能事件概率：关于一个随机事件 A 我们把表示其发生可能性大小的数值称为随机事件 A 发生的概率 ,记为 P（A）发生的结果数P= 全部等可能的结果数（ P 是概率的英文单词probability首字母）。

比、比例和百分比班级_______姓名_______一、 比和比的基本性质1、比：a 、b 是两个数或两个同类的量,为了把b 和a 相比较,将a 与b 相除, 叫做与的比;记作a ：b ,或写成ba ,其中0≠b ；读作a 比b ,或a 与b 的比；a 叫做比的前项,b 叫做比的后项 2、比值：比的前项a 除以后项b 所得的商．叫做比值如4：6＝32,32是4：6的比值 3、比的基本性质：比的前项和后项同时乘以或除以相同的数0除外,比值不变 例题1：求下列各比的比值：19：15 2： 316时：2天 4212：54 例题2：化简下列各比：148：64 2220cm ：1.1m 331：41：61 4： 例题3：利用下列已知条件,求a ：b ：c1a ：b ＝5：3,b ：c ＝2：3 2a ：b ＝21：31,b ：c ＝：； 二、 比例和比例的基本性质1、比例：表示两个比相等的式子叫做比例；即：a ,b ,c ,d 四个量中,如果a ：b ＝c ：d ,那么就说a ,b ,c ,d 成比例；其中a ,b ,c ,d 分别叫做第一、二、三、四比例项,a ,d 叫做比例外项,b ,c 叫做比例内项;2、比例中项：如果两个比例内项相同,即a ：b ＝b ：c ,那么把b 叫做a 和c 的比例中项3、比例的基本性质：如果a ：b ＝c ：d 或dc b a =,那么bc ad =. 反之,如果a ,b ,c ,d 都不为零,且bc ad =,那么a ：b ＝c ：d 或dc b a = 例题1：将已知比例532=x ,改写成以x 为第四比例项的比例式是____________ 例题2：当x 取何值时,它与2、3、4可以组成一个比例例题3：求下列各式中的x ：1x ：511416=：2 2x ：5＝75 34350=x 例题4：小明步行8千米需要2小时,如果以同样的速度步行14千米,那么需要多少小时 例题5：1300千米,那么地图上上海到北京的距离约是多少厘米三、 百分比的意义1、百分比：把两个数量的比值写成100n 的形式,称为百分数,也叫百分比或百分率,记作n ％. 2、小数化成百分数：将小数点向右移两位,同时在右边添上百分号如：4747.0→％,8.2028.0→％,27373.2→％,303.0→％3、百分数化成小数：将％前数字的小数点向左移两位,同时去掉后面的百分号如402.0%2.40→,252.1%2.125→,0052.0%52.0→,2%200→例题1：把下列各数化成百分数：除不尽的在百分号前保留一位小数1006.0 252 3431 42 532 6 例题2：将下列百分数化成小数或整数：13％ 2％ 3200％ 4％ 5120％例题3：将下列百分数化成分数：125％ 2％ 355％ 4％ 5135％。

算术技巧如何快速计算百分比和比例在日常生活中，百分比和比例是常见的数学概念。

无论是在商业领域、金融领域还是日常生活中，我们都需要用到百分比和比例来进行计算。

然而，对于一些人来说，计算百分比和比例可能是一个挑战。

在本文中，我将介绍一些算术技巧，帮助大家快速计算百分比和比例。

一、计算百分比计算百分比是一种常见的数学运算。

我们经常遇到这样的情况：需要计算一个数值占另一个数值的百分比。

下面是一些用于计算百分比的技巧：1. 利用分数和乘法计算一个数值占另一个数值的百分比，可以将百分数看作一个分数，分子为所需的数值，分母为总数。

然后将此分数乘以100，即可得到百分比。

例如，计算28占40的百分比，可以用以下步骤进行计算：28/40 × 100% = 70%所以，28占40的百分比为70%。

2. 利用小数和乘法另一种计算百分比的方法是将百分数转化为小数，并将其乘以所需的数值。

例如，计算115占230的百分比，可以进行以下计算：115 × 100/230 = 50%所以，115占230的百分比为50%。

3. 百分比之间的转换有时候我们需要将一个数值从百分数转换为小数，或者从小数转换为百分数。

这可以通过将百分数除以100，或者将小数乘以100来实现。

例如，将0.75转换为百分数，可以进行以下计算：0.75 × 100 = 75%所以，0.75可以表示为75%。

二、计算比例比例是用于比较两个或多个数值之间的关系。

计算比例可以帮助我们了解不同数值之间的相对大小。

下面是一些用于计算比例的技巧：1. 利用分数和乘法计算比例时，我们可以将比例看作一个分数，并将其乘以所需的数值，即可得到相应的比例值。

例如，计算20和100的比例，可以进行以下计算：20/100 = 1/5所以，20和100的比例为1:5。

2. 利用十进制和乘法另一种计算比例的方法是将比例值表示为十进制，并将其乘以所需的数值。

例如，计算2.5和5的比例，可以进行以下计算：2.5 × 5 = 12.5所以，2.5和5的比例为1:2.5。

百分数和比例百分数和比例是在数学中常见且十分重要的概念。

它们在日常生活中的应用广泛，不仅在商业、经济、统计学等领域中扮演重要角色，也在个人生活中起到了至关重要的作用。

本文将从百分数和比例的概念、计算方法以及实际应用等方面进行阐述。

一、百分数的概念及计算方法百分数是指以100为基数的数，常用百分号“%”表示。

百分数可以看作是比例数的一种特殊形式，其中分子是百分比的数，分母是100。

我们可以通过以下步骤来计算一个数的百分数：1. 将百分数表示成一个分数，分母为100；2. 将待求的数作为分母，分子为分数的分子；3. 将分子与分母相除，得到的商即为百分数。

例如，如果要计算60的百分数，我们可以进行如下计算：60 ÷ 100 = 0.6，再将0.6乘以100，得到60%。

因此，60的百分数为60%。

二、比例的概念及计算方法比例是指两个或多个数之间的相对关系。

常用“:”或“/”符号表示比例。

比例常用于表示实际事物之间的对应关系，如人口比例、物体的比例尺等。

计算比例时，我们可以采用以下方法：1. 将比例中的两个数，分别作为分子和分母；2. 将分子和分母同时除以它们的最大公约数，得到最简形式的比例。

举个例子，如果要计算30和60的比例，我们可以进行如下计算：30 ÷ 30 = 1，60 ÷ 30 = 2。

因此，30和60的比例为1:2。

三、百分数和比例的转换百分数和比例之间存在着密切的联系，它们可以互相转换。

在实际问题中，我们常常需要将百分数转换为比例，或者将比例转换为百分数。

下面以具体的例子来说明这个过程：例1：将百分数75%转换为比例。

步骤一：将百分数表示成一个分数，分母为100。

75%可以表示为75/100；步骤二：将分子和分母同时除以它们的最大公约数，得到最简形式。

75和100的最大公约数为25，因此，75%转换为比例为3:4。

例2：将比例5:6转换为百分数。

步骤一：将比例中的两个数，分别作为分子和分母。

比的应用知识点比作为一个基本的数学概念，被广泛应用在日常生活和各个领域中。

比的概念涵盖了比较大小、比例关系、百分比等方面，对于解决实际问题和理解数学关系都具有重要的作用。

本文将围绕比的基本概念、应用知识点和相关问题进行阐述。

一、基本概念：1. 比的定义：比是用来表示两个数的大小关系的数学符号，通常用字母或符号表示。

a:b表示a与b的比。

2. 比的性质：- 同比：如果a:b=c:d，那么a与b的比等于c与d的比。

- 反比：如果a:b>c:d，那么a与b的比大于c与d的比。

- 复合比：比例中既有直接比又有间接比。

- 比的互换：如果a:b=b:c，那么a、b、c成等比例。

3. 等比数列：如果一个数列中任意相邻的两项的比都相等，那么这个数列就是等比数列。

二、应用知识点：1. 比例关系：比例关系是指两个或多个量之间的相等比例关系。

在实际应用中，常见的比例关系包括人口与面积的关系、速度与时间的关系、金钱与物品的关系等。

根据比例关系可以计算物品的单价、折扣、利润等。

2. 百分比：百分比是指百分数与某个数量之间的数学关系。

在实际应用中，常用于表示比率、增长率、减少率等。

某商品的售价打8折，可以用百分比来表示为80%的售价。

3. 比例定理和相似三角形：比例定理是指在三角形中，如果一条直线平行于另一条边，则它所切割的两边的各对应部分成比例。

相似三角形是指三角形的对应角相等，对应边成比例。

通过这些定理可以求解各种三角形中的长度和角度关系问题。

4. 比的图形表示：比可以通过图形表示出来，比如长方形的宽和长的比例关系可以用长方形的长宽表示，圆的直径和周长的比例可以用圆的直径和周长的图形表示。

图形表示可以直观地展示出比的大小关系，便于理解和应用。

三、相关问题：1. 如何判断两个比例是否相等？判断两个比例是否相等，可以比较其分数值，也可以交叉相乘求等式两边的积是否相等。

2. 如何应用比例定理解决实际问题？比例定理常应用于解决三角形内部长度比例问题，可以通过画图或者推导公式来解决各种实际三角形问题。

比的性质及应用比是一种常见的数学概念，用于判断两个数之间的大小关系。

在数学中，比的性质与应用十分重要，本文将对比的性质进行介绍，以及比在实际生活中的应用。

一、比的定义与性质比是刻画两个数的大小关系的一种数学概念，通常使用符号“:”来表示。

对于两个数a和b来说，如果可以用一个较大的整数n去乘以a，得到的结果等于b，我们就可以说a与b之间存在比。

比的定义可以表示为：若存在自然数n，使得a×n=b，则称a与b之间存在比，记作a:b。

比的性质如下：1. 对称性：若a:b，则b:a。

2. 传递性：若a:b，b:c，则a:c。

3. 三线性：若a:b，c:d，则a+c:b+d。

4. 基本比：任何数与0之间都不存在比。

若a:b，并且b≠0，则a与b之间的比是不唯一的。

二、比的应用比在实际生活中有着广泛的应用，以下是其中几个常见的应用场景：1. 比例与比例问题：比例是比的一种常见应用形式，它可以用来描述两个或多个数之间的等比关系。

比例在实际问题中经常被用于计算和解决各种比例问题，如物理问题中的速度、距离比例，商业问题中的价格比等。

2. 百分比：百分比是比的一种特殊形式，常用于表示一部分与整体之间的比例关系。

在商业、经济、统计等领域中，百分比被广泛应用于数据分析和统计，如表示增长率、利润率、市场份额等。

3. 相似形状：比可以用于描述几何形状之间的相似关系。

当两个几何形状的对应线段之间的比相等时，我们可以说它们是相似的。

相似性在几何学中有着广泛的应用，例如在工程图纸中的比例尺，人体模型的缩小比例等。

4. 货币兑换：比可以用于货币兑换问题中，帮助计算不同货币之间的汇率。

汇率即两种货币之间的兑换比例，通过比的概念可以很方便地进行货币之间的转换计算。

5. 比较大小：比可以直接用于比较不同数值的大小关系。

通过比的概念，我们可以准确地判断两个数值之间的大小关系，帮助我们进行有效的比较和排序。

综上所述，比作为一种数学概念，在数学中具有重要的性质，例如对称性、传递性和三线性。

比例的计算方法与应用举例比例是数学中常用的一种量度关系方法，用于描述两个或多个数量之间的相对大小关系。

在实际生活和工作中，比例的计算方法和应用非常广泛。

本文将介绍比例的计算方法，并通过一些实际例子来展示比例的应用。

一、比例的计算方法比例通常以两个数的比值表示，可以用两种形式来表示，即比值形式和百分比形式。

1. 比值形式比值形式表示两个数的比例关系，如a:b，可以理解为a和b之间的比值为a/b。

在计算机科学中，比值形式常用于表示图像分辨率、屏幕长宽比等。

使用比值形式计算比例时，首先确定某一数值作为基准值，然后将另一个数值与基准值相除得到比例。

举例说明：某人拥有1000美元，他计划用其中的一部分购买苹果手机。

4部手机的价格是3200美元，请计算他可以购买多少部手机。

解答：设他可以购买x部手机，则比例关系为3200:1000 = 4:x。

通过交叉相乘得到3200x = 4 * 1000，进而得到x = (4 * 1000) / 3200 =1.25。

因此，他可以购买1.25部手机。

2. 百分比形式百分比形式是将两个数之间的比例关系表示为百分数。

在统计分析、经济学等领域中，百分比形式常用于表示增长率、通胀率等。

使用百分比形式计算比例时，将两个数之间的比例关系表示为百分数，即将比值形式的结果乘以100并附上百分号。

举例说明：某公司在去年实现销售额为200万美元，今年实现销售额为250万美元，请计算今年的销售额相较于去年的增长率。

解答：设去年的销售额为a，今年的销售额为b，则比例关系为a:b = 200:250。

通过交叉相乘得到200b = 250 * a，进而得到b/a = 250/200= 1.25。

将比值形式转化为百分比形式，增长率为1.25 * 100% = 125%。

因此，今年的销售额相较于去年增长了25%。

二、比例的应用举例1. 车辆油耗比例计算假设某辆汽车上一次加满油行驶了400公里，使用了30升的汽油。

比多少的数学题
"比多少"是一个常见的数学问题类型，常见于比例和百分比的应用中。

这类问题涉及两个数之间的比较，通常需要计算或确定两个数的比值或比例关系。

以下是比多少数学题的一些例子：
1. 求比率或比例：
•例子：甲园有苹果80个，乙园有苹果120个，问乙园苹果比甲园多了多少？
2. 百分比问题：
•例子：如果一个班级有40名男生和60名女生，男生人数占全班学生人数的比例是多少？
3. 增长或减少的百分比：
•例子：如果商品原价是100元，现在打8折出售，折扣了多少？
4. 分数和小数的比较：
•例子： 0.75和3/4哪个更大？
这些题目旨在考察学生对数值关系、比较大小、百分比和比例的理解和应用能力。

解决这些问题需要学生具备对比、计算和分析的能力，同时灵活运用基本的数学运算和比较大小的方法。

让你轻松认识各种比例关系比例关系在我们的日常生活中无处不在，了解和掌握各种比例关系对我们的学习和生活都有着很大的帮助。

本文将为您介绍一些常见的比例关系，并提供一些简单易懂的例子，帮助您轻松理解和认识各种比例关系。

一、比例与比例的表示方法比例是两个相同类型的量之间的等比关系。

比例关系可以用等比例符号“：”表示，也可以用分数表示。

例如，中国和美国的人口比例为4：1，可以表示成4/1或4.0。

二、直接比例关系直接比例关系是指两个量成正比，即当一个量增大时，另一个量也相应地增大；当一个量减小时，另一个量也相应地减小。

直接比例关系可以用以下公式表示：y = kx其中，y和x表示两个量，k为比例常数。

举例来说，如果一辆汽车以每小时60公里的速度行驶，那么行驶时间与行驶距离之间就存在直接比例关系。

行驶时间与行驶距离之间的比例常数k为1/60或0.0167。

三、反比例关系反比例关系是指两个量成反比，即当一个量增大时，另一个量相应地减小；当一个量减小时，另一个量相应地增大。

反比例关系可以用以下公式表示：y = k/x其中，y和x表示两个量，k为比例常数。

例如，如果一个水桶被用来接水，水龙头的流量与接满水桶所需的时间之间存在反比例关系。

水龙头的流量与接满水桶所需的时间之间的比例常数k为1。

四、相似比例关系相似比例关系是指在两个或多个几何形状之间存在的比例关系。

在相似的图形中，其边长、面积或体积等各个部分之间的比例关系相同。

例如，两个三角形ABC和DEF是相似的，可以表示为ABC∼DEF。

在这种情况下，三角形ABC的边长与三角形DEF的边长之间的比例关系为AB/DE = BC/EF = AC/DF。

五、百分比关系百分比关系是指将一个数表示为另一个数的百分之几。

百分比关系可以用以下公式表示：百分比 = (部分/整体) × 100%例如，如果一个班级有30名男生和40名女生，那么男生所占的百分比为(30/70) × 100% = 42.9%，女生所占的百分比为(40/70) × 100% =57.1%。

关于比例与百分比的故事从古老的希腊神话到现代生活中的种种比喻，比例与百分比无疑是我们生活中不可或缺的一部分。

它们可以描述数量的关系，帮助我们理解事物的大小和比较不同的数据。

本文将通过一系列的故事，带您领略比例与百分比的魅力，并了解它们在各个领域的应用。

故事一：伊卡洛斯的轨迹在古希腊神话中，伊卡洛斯是代达罗斯的儿子，他们被困在克里特岛上。

为了逃离岛屿，他们制作了一对翅膀，用蜡和鹅毛粘合而成。

他们得到了解脱，但代达罗斯提醒伊卡洛斯不要飞得太高，否则太阳会融化他的翅膀。

然而，伊卡洛斯无法抵挡对自由的渴望，最终飞得太高，蜡翅膀融化了，他坠入了大海中。

这个故事给我们带来了一个关于比例的启示：一定要记住自己的限制。

就像伊卡洛斯一样，如果我们超越了能力所及的范围，可能会有危险。

这种警戒意识也适用于我们生活中的各个领域。

比如在财务投资中，我们需要合理地设置风险承受能力的上限，以避免遭受过大的损失。

通过比例，我们可以更好地把握自己与世界的关系，避免过于自负或过于谨慎。

故事二：大卫与歌利亚大卫与歌利亚的故事源自圣经。

大卫是以色列的一位农夫，身材只有儿童般大小，而歌利亚则是强大的非利士人军队的战士。

在两军对垒的时候，歌利亚挑衅大卫，但大卫凭借精准的投石器将歌利亚打败。

这个故事告诉我们关于百分比的一些事情。

众所周知，大卫在击败歌利亚之前被认为是弱小的，但他成功地抓住了对手的弱点并利用了自己的技术优势。

在现实生活中，我们也常常遇到类似的情况。

人们往往只看到事物的表面，却忽视了其中的细节和比例关系。

通过百分比，我们可以更细致地分析和理解问题，找到解决问题的方法和策略。

故事三：艾琳的奋斗艾琳是一位有着梦想的年轻女孩，她热爱音乐并梦想成为一名钢琴家。

然而，由于家境贫寒，她无法接受专业的音乐培训。

艾琳没能放弃她的梦想，她每天用零花钱租一台钢琴并自学钢琴技巧。

她把每一个练习都当成一次机会，一点一滴地提升自己。

最终，她考入了一所著名音乐学院，成为一名优秀的钢琴家。

求比值的方法公式1. 比值计算公式：比值 = 比值的分子 / 比值的分母2. 百分比公式：百分比 = 比值× 100%3. 比例公式：比例 = 比值的分子 : 比值的分母4. 步行速度比公式：步行速度比 = 步行的距离1 / 步行的时间1 : 步行的距离2 / 步行的时间25. 阳光照射面积比公式：阳光照射面积比 = 阳光照射面积1 / 阳光照射面积26. 体积比公式：体积比 = 物体A的体积 / 物体B的体积7. 数量比公式：数量比 = 物品A的数量 / 物品B的数量8. 速度比公式：速度比 = 物体A的速度 / 物体B的速度9. 投资回报率公式：投资回报率 = （收益 - 成本）/ 成本× 100%10. 利润率公式：利润率 = 利润 / 销售额× 100%11. 增长率公式：增长率 = 新值 - 旧值 / 旧值× 100%12. 学生比例公式：学生比例 = 学生人数 / 教师人数13. 股票收益率公式：股票收益率 = （股价 - 购入成本）/ 购入成本× 100%14. 税率公式：税率 = 税收金额 / 收入金额× 100%15. 人数比例公式：人数比例 = 某人数 / 总人数× 100%16. 利息率公式：利息率 = 利息 / 本金× 100%17. 客流量比公式：客流量比 = 地铁A的客流量 / 地铁B的客流量18. 地区面积比公式：地区面积比 = 地区A的面积 / 地区B的面积19. 销售增长率公式：销售增长率 = （销售额的新值 - 销售额的旧值）/ 销售额的旧值× 100%20. 支出占比公式：支出占比 = 某支出项 / 总支出× 100%21. 人口密度公式：人口密度 = 居民人口数 / 地区面积22. 体重指数公式：体重指数 = 体重 / 身高的平方23. 年度增长率公式：年度增长率 = （年度新值 - 年度旧值）/ 年度旧值× 100%24. 债务率公式：债务率 = 债务 / 总资产× 100%25. 出生率公式：出生率 = 出生人数 / 人口数× 100%26. 火车距离比公式：火车距离比 = 火车A的距离 / 火车B的距离27. 高速公路车流量比公式：高速公路车流量比 = 高速公路A的车流量 / 高速公路B的车流量28. 员工满意度比公式：员工满意度比 = 公司A的员工满意度 / 公司B的员工满意度29. 进口比例公式：进口比例 = 进口额 / 出口额× 100%30. 电力消耗比公式：电力消耗比 = 用电量A / 用电量B31. 养老金比例公式：养老金比例 = 某年养老金支出 / 年平均工资× 100%32. 电视收视率公式：电视收视率 = 收看某频道的人数 / 总人数× 100%33. 班级男女比例公式：班级男女比例 = 男生人数 / 女生人数34. 研发投入占比公式：研发投入占比 = 研发投入 / 总成本× 100%35. 产品市场占有率公式：产品市场占有率 = 产品销售额 / 行业总销售额× 100%36. 交通事故发生率公式：交通事故发生率 = 交通事故次数 / 行驶里程× 100%37. 突发事件处理效率公式：突发事件处理效率 = 处理事件数 / 接到事件数× 100%38. 流动比率公式：流动比率 = 流动资产 / 流动负债39. 客户满意度比公式：客户满意度比 = 客户满意度A / 客户满意度B40. 网站流量比公式：网站流量比 = 网站A的流量 / 网站B的流量41. 商品价格比公式：商品价格比 = 商品价格A / 商品价格B42. 采购成本占比公式：采购成本占比 = 采购成本 / 总成本× 100%43. 学校录取率公式：学校录取率 = 录取人数 / 报名人数× 100%44. 客户保留率公式：客户保留率 = 保留的客户数 / 初始客户数× 100%45. 员工流动率公式：员工流动率 = 未续约员工数 / 平均员工数× 100%46. 设备利用率公式：设备利用率 = 实际运行时间 / 计划运行时间× 100%47. 旅游收入比公式：旅游收入比 = 旅游收入A / 旅游收入B48. 存货周转率公式：存货周转率 = 销售成本 / 平均存货× 100%49. 基金收益率公式：基金收益率 = （基金净值变动 - 分红）/ 基金净值× 100%50. 银行贷款利率公式：银行贷款利率 = 利息 / 贷款金额× 100%。

六年级比和百分数知识点比的概念和运算规则：比是用来比较两个或多个数值大小关系的数学概念。

在六年级数学中，比的概念和运算规则是一个重要的知识点。

比数由冒号“:”连接，比的两个数称为比的项。

比的项的顺序不同，比的结果也会不同。

比的大小关系的判断方法：1. 如果比的项相等，那么比也相等。

例如：2:3 = 2:32. 如果比的项都相等，那么它们的比相等。

例如：2:3 = 4:63. 如果比的项比例相等，那么它们的比相等。

例如：2:3 = 4:6 = 6:9比的应用：比的应用广泛，例如在实际生活中计算和表示比例关系、图形的放大和缩小比例等等。

比的应用需要我们用到数学知识和技巧，同时要能够理解和分析具体问题。

百分数的概念和表示法：百分数是表示数值相对于100的百分比形式。

在六年级数学中，百分数的概念和表示法是重要的知识点。

百分数可以用小数或分数形式表示。

百分数和小数的相互转化：1. 百分数转化为小数：将百分数除以100，并去掉百分号，得到的结果就是相应的小数。

例如：60% = 60/100 = 0.62. 小数转化为百分数：将小数转化为百分数，需要将小数乘以100，并加上百分号。

例如：0.6 = 0.6 × 100% = 60%百分数和分数的相互转化：1. 百分数转化为分数：将百分数除以100，再将百分号去掉，得到的结果即为相应的分数。

例如：40% = 40/100 = 2/52. 分数转化为百分数：将分数转化为百分数，需要将分数化为小数形式，然后再按照小数转化为百分数的方法进行换算。

例如：2/5 = 2÷5 = 0.4 = 0.4 × 100% = 40%百分数的运算：在百分数的运算中，我们会涉及到百分数的加减乘除。

具体的运算规则如下：1. 百分数的加减：将相同的单位转化为百分数，然后按照整数的加减法进行计算。

例如：40% + 30% = 70%2. 百分数的乘法：将百分数转化为小数，然后按照小数的乘法运算规则进行计算，最后再换算成百分数。

比例的名称数学是一门充满着奥妙和美妙的学科，而比例是其中最基础和最重要的一个概念。

比例指的是两个或多个量的大小关系，它们按照一定的规律配比而成。

比例有许多相关的名称，下面将介绍几个比较常见的。

一、比率比率是指两个有量纲的量之间的比值，即两个数量的相对大小关系。

比率通常用分号表示，比如“男女比为3：2”，其中3和2就是男女的比率。

另外，比率还可以写成百分数的形式，比如“男女比为60%：40%”，表示男女比率的百分比。

二、比例比例是指两个或多个量之间的相对大小关系，它们按照一定的规律配比而成。

比例是一个无量纲的量，通常用冒号表示，比如“男女比例为3：2”。

比例可以用分数的形式表示，比如“男女比例为3/5”，也可以写成百分数的形式，比如“男女比例为60%：40%”。

三、倍数倍数是指一个数是另一个数的几倍，即两个量之间的数量关系。

例如，如果说一个人的年收入是10万元，而另一个人的年收入是20万元，那么后者的收入就是前者的2倍。

倍数通常用“×”符号表示，比如“20万元是10万元的2倍”。

四、百分比百分比是指一个数相对于另一个数的百分比，即一个量在总量中的占比。

百分比通常用“%”符号表示，比如“男生占总人口的比例为40%”。

百分比是一个无量纲的量，它可以转化为比率、比例或者小数的形式。

五、分数分数是指一个量相对于总量的比值，它通常用一个分子和一个分母表示。

例如，“1/2”表示一个量相对于总量的一半，而“3/4”表示一个量相对于总量的四分之三。

分数也可以转化为比率、比例或者百分比的形式。

总之，比率、比例、倍数、百分比和分数是数学中比较基础和常见的比例概念。

它们在日常生活和各个领域中都有广泛的应用，如商业、金融、工程、科学等等。

对于一个数学学习者来说，掌握这些比例概念的含义和应用，是很有必要的。

比例的八个变式比例的八个变式是统计学中常用的一种分析方式，它通过比较数量或比较大小来评估不同属性之间的关系，从而对特定情况进行分析或预测。

在研究工作中，比例的八个变式通常用于检验和比较不同类别的样本是否具有相同的特征。

比例的八个变式包括：比例分布、比例比、正比例比、反比例比、比例加总比、比例比加总比、百分比变式和比例分析法。

1、比例分布：比例分布是根据抽样数据，将可能出现的所有结果（如区域、国家、民族等）以及它们的比例用表格的形式做一个汇总，以便比较不同类别的样本的比例变化情况。

2、比例比：比例比是比较两个或多个样本中某一项属性的比例，以表明其差异或相似之处。

它可以用来比较不同时期的比例，也可以用来比较不同地区的比例。

3、正比例比：正比例比是比较两个或多个样本中某一项属性的比例，以表明其相似之处。

在正比例比中，如果两个样本的比例相同，则说明两个样本具有相似的特征。

4、反比例比：反比例比是一种比较两个或多个样本中某一项属性的比例，以表明其差异之处的方法。

在反比例比中，如果两个样本的比例不同，则说明两个样本具有不同的特征。

5、比例加总比：比例加总比是比较两个或多个样本中某一项属性的比例，以表明其总体差异的方法。

它常用于对比不同时期或不同地区的全球和总体情况。

6、比例比加总比：比例比加总比是比较两个或多个样本中某一项属性的比例，以表明其总体和部分差异的方法。

它常用于对比不同时期或不同地区的全球和分区情况。

7、百分比变式：百分比变式是比较两个或多个样本中某一项属性的比例，以表明其占比的方法。

它常用于研究不同数据集的比例变化情况，以及各数据集中哪些数据占据比重最大。

8、比例分析法：比例分析法是比较两个或多个样本中某一项属性的比例，以表明其占比及其变化情况的方法。

它可以用来比较不同时期或不同地区的数据，以及对比数据在不同时期间和不同地区间的变化情况。

以上是比例的八个变式的详细说明。

比例变式在统计学中应用广泛，它可以帮助我们更好地理解数据，并从中得出重要的结论。

数字的百分比用百分数表示数字的比例百分比是我们日常生活中经常会遇到的概念，是数学中的一种表示方式。

通过百分比，我们可以很直观地了解到一个数量相对于另一个数量的比例关系，它既可以用于描述增长或减少的趋势，也可以用于比较不同组别之间的差异。

在本文中，我们将探讨数字的百分比以及如何用百分数来表示数字的比例。

一、什么是百分比？百分比是一种表示数值相对数量的方式，它将一个数值表示为另一个数值的百分之几。

百分比常用百分号“%”来表示。

例如，如果说某项业务的收入增长了20%，那么意味着收入增加了原来的20%。

百分比的概念可以帮助我们更清晰地了解事物的快慢、多少等相对概念。

二、如何计算百分比？计算百分比的方法非常简单，可以通过以下公式来完成：百分比 = (具体数值 / 总数值) × 100%具体数值是我们想要表达的数字，总数值是与之相关的完整的量或对象。

通过上述公式，我们可以计算出百分比，并对数据进行比较和分析。

下面通过几个示例来说明计算百分比的具体步骤。

例1：某学校共有500名学生，其中男生300人，女生200人。

那么男生所占的百分比是多少？男生的人数为300，总人数为500，带入公式计算：百分比 = (300 / 500) × 100% = 60%因此，男生所占的百分比为60%。

例2：某家公司去年的销售额为1000万元，今年的销售额增长到1500万元。

今年的销售额相比去年增长了多少百分比？去年销售额为1000万元，今年销售额为1500万元，带入公式计算：百分比 = ((1500 - 1000) / 1000) × 100% = 50%因此，今年的销售额相比去年增长了50%。

通过这两个例子，我们可以看到百分比的计算方法可以帮助我们更好地理解和比较数据，从而更深入地分析问题。

三、百分数的应用百分数广泛应用于各个领域，包括商业、经济、统计和日常生活中。

下面列举几个常见的应用场景：1. 商业中的市场份额比较：公司A去年的市场份额为20%，今年提升至30%。