第六节向心加速度
- 格式:doc
- 大小:45.00 KB
- 文档页数:2








第六节向心加速度知识与技能1.理解速度变化量和向心加速度的概念。
2.知道向心加速度和线速度、角速度的关系式。
3.能够运用向心加速度公式求解有关问题。
过程与方法1.体验向心加速度的导出过程。
2.领会推导过程中用到的数学方法。
情感、态度与价值观培养学生思维能力和分析问题的能力,培养学生探究问题的热情、乐于学习的品质。
【教学重点】1.理解匀速圆周运动中加速度的产生原因。
2.掌握向心加速度的确定方法和计算公式。
【教学难点】向心加速度方向的确定过程和向心加速度公式的应用【教学课时】1课时【教具准备】多媒体课件、实物投影仪等。
教学过程【引入新课】情景导入-(1分钟)通过前面的学习我们知道在现实生活中,物体都要在一定的外力作用下才能做曲线运动,如下列两图:对于图中的地球和小球,它们受到了什么样的外力作用?它们的加速度大小和方向如何确定? 【进行新课】一、速度变化量-(5分钟)引入:从加速度的定义式a=tv∆∆可以看出。
a 的方向与v ∆相同,那么v ∆的方向又是怎么样的呢?1.指导学生学生阅读教材中的“速度变化量”部分,引导学生在练习本上画出物体加速运动和减速运动时速度变化量v ∆的图示。
问题:1.速度的变化量v ∆是矢量还是标量?2.如果初速度v 1和末速度v 2不在同一条直线上,如何表示速度的变化量v ∆?结论:(1)直线运动中的速度变化量如果速度是增加的,它的变化量与速度方向相同(甲);如果速度是减少的,其速度变化量就与初速度的方向相反(乙)。
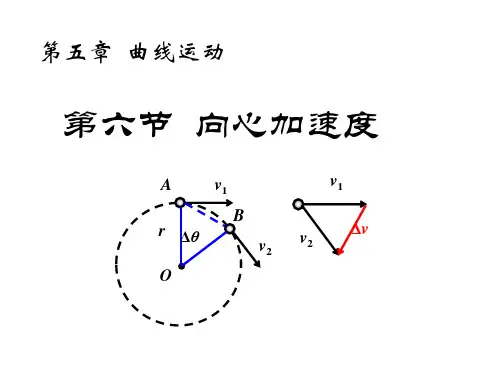
(2)曲线运动中的速度变化量物体沿曲线运动时,初速度v1和v2不在同一直线上,初速度的变化量v∆同样可以用上述方法求得。
例如,物体沿曲线由A向B运动,在A、B两点的速度分别为v1和v2。
在此过程中速度的变化量如图所示:可以这样理解:物体由A运动到B时,速度获得一个增量v∆,因此,v1与v∆的矢量和即为v2。
我们知道,求力F1、F2的合力F时,可以以F1、F2为邻边作平行四边形,则F1、F2所夹的对角线就表示合力F。

第六节 向心加速度
【知能准备】
v 0表示初速度,v 表示末速度,则速度变化量Δv = 。
加速度公式a = ,其方向与速度变化量方向 。
-v 0 0(填“>”或“<”),其方向与初速度方向 ;假如速度减小,Δv =v -v 0
3.在曲线运动中,速度变化量Δv 与始末两个速度v 0、v 的关系:_______________________ ____________。
4.在圆周运动中,线速度、角速度的关系是 。
【典型例题】
例1 一质点沿着半径r = 1 m 的圆周以n = 1 r/s 的转速匀速转动,如图,试求:
(1) 从A 点开始计时,经过0.25s 的时间质点速度的变化;
(2) 质点的向心加速度的大小。
例2 关于向心加速度,以下说法准确的是( )
A .它是描绘角速度变化快慢的物理量
B .它是描绘线速度大小变化快慢的物理量
C .它是描绘线速度方向变化快慢的物理量
D .它是描绘角速度方向变化快慢的物理量 例3 如下图为质点P 、Q 做匀速圆周运动时向心加速度随半径变化的图线,表示质点P 的图线是双曲线,表示质点Q 的图线是过原点的一条直线。
由图线可知( )
A .质点P 线速度大小不变
B .质点P 的角速度大小不变
C .质点Q 的角速度随半径变化
D .质点Q 的线速度大小不变
例4 如下图,一球体绕轴O 1O 2以角速度ω旋转,A 、B 为球体上两点。
以下说法中准确的是( )
A .A 、
B 两点具有相同的角速度
B .A 、B 两点具有相同的线速度
C .A 、B 两点具有相同的向心加速度
D .A 、B 两点的向心加速度方向都指向球心
【课堂练习】
1.因为地球的自转,地球表面上各点均做匀速圆周运动,所以
( )
A .地球表面各处具有相同大小的线速度
B .地球表面各处具有相同大小的角速度
C .地球表面各处具有相同大小的向心加速度
D .地球表面各处的向心加速度方向都指向地球球心
2.以下关于向心加速度的说法中,准确的是( )
A .向心加速度的方向始终与速度的方向垂直
B .向心加速度的方向保持不变
C .在匀速圆周运动中,向心加速度是恒定的
D .在匀速圆周运动中,向心加速度的大小持续变化
3.因为地球自转,比较位于赤道上的物体1与位于北纬60°的物体2,则( )
A .它们的角速度之比ω1∶ω2=2∶1
B .它们的线速度之比v 1∶v 2=2∶1
C .它们的向心加速度之比a 1∶a 2=2∶1
D .它们的向心加速度之比a 1∶a 2=4∶1
O A r (例1) (例3) (例4)
4.关于质点做匀速圆周运动的以下说法准确的是()
A.由a=v2/r,知a与r成反比 B.由a=ω2r,知a与r成正比
C.由ω=v/r,知ω与r成反比 D.由ω=2πn,知ω与转速n成正比
5.A、B两小球都在水平面上做匀速圆周运动,A球的轨道半径是B球轨道半径的2倍,A 的转速为30r/min,B的转速为15r/min。
则两球的向心加速度之比为()
A.1:1 B.2:1 C.4:1 D.8:1
6.如下图皮带传动轮,大轮直径是小轮直径的3倍,A是大轮边缘上一点,B是小轮边缘上一点,C是大轮上一点,C到圆心O1的距离等于小轮半径,转动时皮带不打滑。
则A、B、C 三点的角速度之比ωA∶ωB∶ωC = ,向心加速度大小之比a A∶a B∶a C = 。
7.如下图,定滑轮的半径r=2 cm,绕在滑轮上的细线悬挂着一个重物,由静止开始释放,测得重物以加速度a=2 m/s2做匀加速运动。
在重物由静止下落1 m的瞬间,滑轮边缘上的P 点的角速度ω=_____ rad/s,向心加速度a=_____ m/s2。
·P
(第6题)(第8题)
(第7题)
8.如下图,摩擦轮A和B通过中介轮C实行传动,A为主动轮,A的半径为20 cm,B的半径为10 cm,则A、B两轮边缘上的点,角速度之比为_____;向心加速度之比为_____。