函数图像+反函数+基本初等函数(讲义+例题)
- 格式:doc
- 大小:396.50 KB
- 文档页数:5
在数学的发展过程中,形成了最简单最常用的六类函数,即 常数函数 、 幂函数、 指数函数 、 对数函数 、 三角函数 与 反三角函数 ,这六类函数称为 基本初等函数。
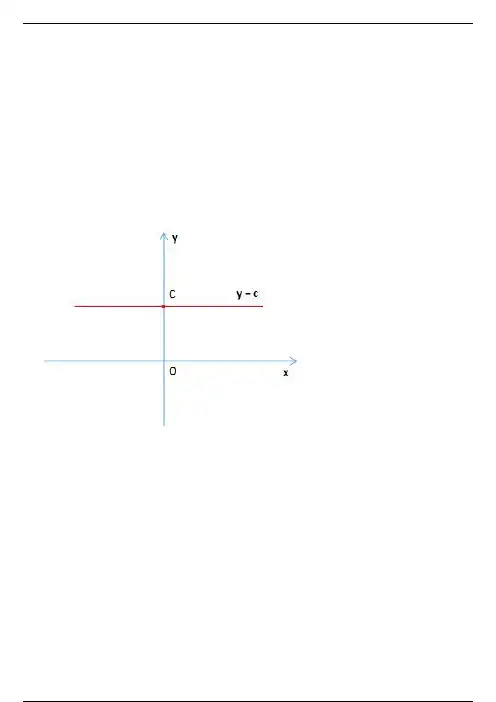
一、常数函数y = c 或 f ( x ) = c , x ∈ R ,其中 c 是常数。
它的图像是通过点 (0,c),且平行 x轴的直线,如下图所示:常数函数的图像常数函数的性质:1、常数函数是有界函数,周期函数(没有最小的正周期)、偶函数;2、常数函数既是单调增加函数又是单调减少函数,特别的当 c = 0 时,它还是奇函数。
二、幂函数1、形如 y = x^a 的函数是幂函数,其中 a 是实数 。
幂函数图(1)2、常见幂函数的图像:幂函数图(2)注:画幂函数图像时,先画第一象限的部分,在根据函数奇偶性完成整个图像。
3、幂函数的性质:① 幂函数的图像最多只能同时出现在两个象限,且不经过第四象限;如图与坐标轴相交,则交点一定是坐标原点 。
② 所有幂函数在 (0,+∞)上都有定义,并且图像都经过点 (1,1)。
③ 若 a > 0 , 幂函数图像都经过点 (0,0)和(1,1),在第一象限内递增;若 a三、指数函数1、一般地,函数 y = a^x (a > 0 且 a ≠ 1)叫做 指数函数 ,自变量 x 叫做 指数 ,a 叫做 底数 ,函数的定义域是 R 。
2、指数函数的图像:指数函数图象3、指数函数的性质:① 指数函数 y = a^x (a > 0 且 a ≠ 1)的函数值恒大于零 ,定义域为 R ,值域为(0,+∞);② 指数函数 y = a^x (a > 0 且 a ≠ 1)的图像经过点 (0,1);③ 指数函数 y = a^x (a > 1)在 R 上递增 ,指数函数 y = a^x (0四、对数函数1、对数及其运算:一般地,如果 a (a > 0 , a ≠ 1)的 b 次幂等于 N ,即 a^b = N,那么 b 叫做以 a 为底N 的 对数 ;记作: log aN = b , 其中 a 叫做对数的 底数 , N 叫做 真数 。
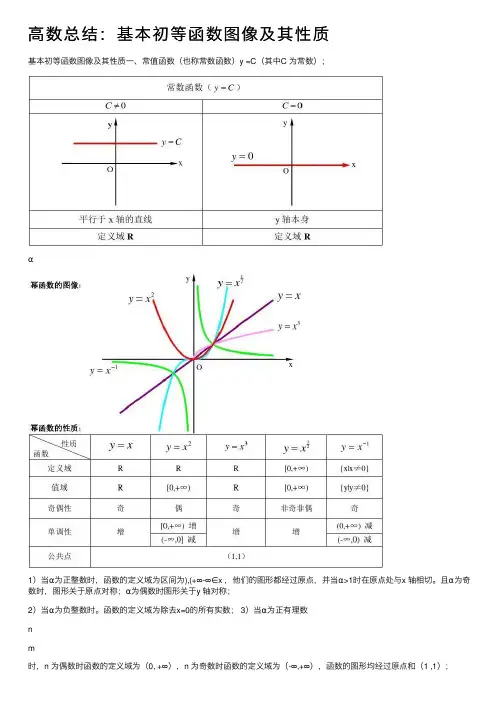
⾼数总结:基本初等函数图像及其性质基本初等函数图像及其性质⼀、常值函数(也称常数函数)y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数n4)如果m>n 图形于x 轴相切,如果m5)当α为负有理数时,n 为偶数时,函数的定义域为⼤于零的⼀切实数;n 为奇数时,定义域为去除x=0以外的⼀切实数。
三、指数函数xa y =(x 是⾃变量,a 是常数且0>a ,1≠a ),定义域是R ;[⽆界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上⽅; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的⼤⼩⽐较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ?=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越⼤,xa y =的图像越靠近y 轴;b.2.当10<的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=?m n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m n m(2))1,,,0(11*>∈>==-n Z n m a a amnm nm yxf x xxx g ?=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [⽆界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式⼦N a log 叫做对数式。

函数图像变换与基本初等函数一、函数的图象与图象交换与图象的对称点坐标函数解析式对称性关于x轴对称(x,y)与(x,-y)关于y轴对称(x,y)与(-x,y)关于原点对称(x,y)与(―x,―y)关于直线y=x对(x,y)与(y,x)称是偶函数,其图象关于y轴对称,图象在y 轴右侧部分与图象重合。
图象全部在x轴上方(含x轴):保留图象在x 轴上方部分,将图象在x轴下方部分沿x轴翻折上去。
(即作出这部分关于x轴的对称图形)基础例题1、已知函数,且满足,则a=________。
解析:,∴的曲线关于(1,0)点对称。
又是由y=x3左右平移得到的,易知a=-1。
2、利用图象变换画出下列函数的图象(1);(2);(3)。
解析:(1)∴的图象可由的图象向右平移一个单位得。
(2)(3)3、已知函数的图像过点(0,1),那么函数的反函数的图像一定经过下列各点中的()A.(4,―1)B.(1,―4)C.(―4,1)D.(1,4)解析:原函数向左平移,相应反函数向下平移。
答案选B。
4、填空:(1)将函数y=3x2―4x―12的图象沿向量平移后的解析式为__________。
(2)函数与的图像关于直线x=1对称,则________。
解析:(1)∴即∴(2)的图象与图象关于直线x=1对称,即,∴5、若函数在R 上单调递减,则的单减区间为(―2,+∞)。
解析:由复合函数单调性可知,的单减区间即为|x+2|=u的单增区间。
二、几个具体常见的函数二次函数指数函数对数函数解析式,,2,3 ,,2,3 定义域RR (0,+∞)值域、最值a>0,a<0,(0,+∞)R 图象a>0单调性a>0,在递减a<0,在a>0,递增a<0,递减a>1,递增0<a<1,递减递增奇偶对称性b=0时偶非奇非偶非奇非偶反函数无1、设二次函数满足,且图象在y轴上的截距为1,截x轴所得线段的长为,求的解析式。
解析:∴图象关于x=―2对称,∴①图象在y轴截距为1,∴c=1 ②截x轴所得线段长为,即的2根③由①②③可解,b=2,c=1,∴2、已知函数的值域为R,求a的取值范围。
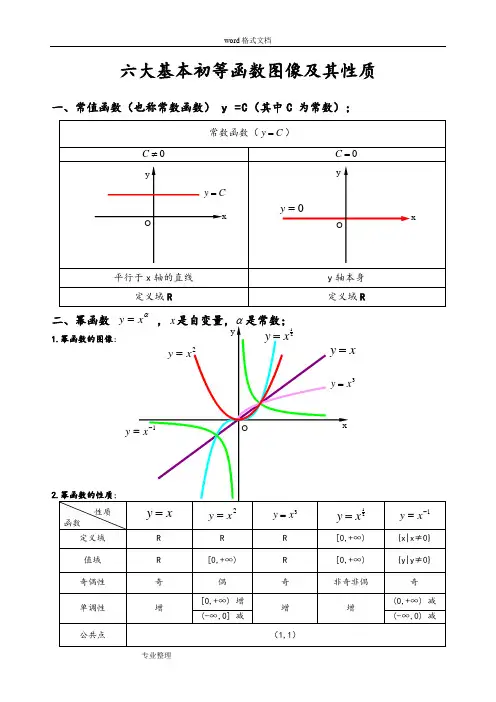
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C(其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a 时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
1(3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数x a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nm n m aa a ==(4) ()nnnba ab =b.根式的性质; (1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂;(1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm yxf x xxx g ⎪⎫⎛=1)(四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。
如,,,都是幂函数。
没有统一的定义域,定义域由值确定。
如,。
但在内总是有定义的,且都经过(1,1)点。
当时,函数在上是单调增加的,当时,函数在内是单调减少的。
下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3。
图1-1-2图1-1-32.指数函数函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。
高等数学中常用的指数函数是时,即。
以与为例绘出图形,如图1-1-4。
图1-1-43.对数函数函数称为对数函数,其定义域,值域。
当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。
与互为反函数。
当时的对数函数称为自然对数,当时,称为常用对数。
以为例绘出图形,如图1-1-5。
图1-1-54.三角函数有,它们都是周期函数。
对三角函数作简要的叙述:(1)正弦函数与余弦函数:与定义域都是,值域都是。
它们都是有界函数,周期都是,为奇函数,为偶函数。
图形为图1-1-6、图1-1-7。
图1-1-6 正弦函数图形图1-1-7 余弦函数图形(2)正切函数,定义域,值域为。
周期,在其定义域内单调增加的奇函数,图形为图1-1-8图1-1-8(3)余切函数,定义域,值域为,周期。
在定义域内是单调减少的奇函数,图形如图1-1-9。
图1-1-9(4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10。
图1-1-10(5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。
图1-1-115.反三角函数反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12;图1-1-12,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图1-1-13;图1-1-13反正切函数,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图1-1-14;图1-1-14为有界函数,在其定义域内单调减少的非奇非偶函数。


五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。
如,,,都是幂函数。
没有统一的定义域,定义域由值确定。
如,。
但在内总是有定义的,且都经过(1,1)点。
当时,函数在上是单调增加的,当时,函数在内是单调减少的。
下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3。
图1-1-2图1-1-32.指数函数函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。
高等数学中常用的指数函数是时,即。
以与为例绘出图形,如图1-1-4。
图1-1-43.对数函数函数称为对数函数,其定义域,值域。
当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。
与互为反函数。
当时的对数函数称为自然对数,当时,称为常用对数。
以为例绘出图形,如图1-1-5。
图1-1-54.三角函数有,它们都是周期函数。
对三角函数作简要的叙述:(1)正弦函数与余弦函数:与定义域都是,值域都是。
它们都是有界函数,周期都是,为奇函数,为偶函数。
图形为图1-1-6、图1-1-7。
图1-1-6正弦函数图形图1-1-7余弦函数图形(2)正切函数,定义域,值域为。
周期,在其定义域内单调增加的奇函数,图形为图1-1-8图1-1-8(3)余切函数,定义域,值域为,周期。
在定义域内是单调减少的奇函数,图形如图1-1-9。
图1-1-9(4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10。
图1-1-10(5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。
图1-1-115.反三角函数反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12;图1-1-12反余弦函数,定义域为[-1,1],值域为,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图1-1-13;图1-1-13反正切函数,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图1-1-14;图1-1-14反余切函数,定义域为,值域,为有界函数,在其定义域内单调减少的非奇非偶函数。

基本初等函数图像及性质六大基本初等函数图像及其性质一、常数函数(也称常值函数)y=C(其中C为常数);常数函数(y=C)是平行于x轴的直线,定义域为R,值域为{C},非奇非偶,单调性为不变,公共点为(0,C)。
二、幂函数y=x^α,x是自变量,α是常数;1.幂函数的图像:当α为正整数时,函数的图像都经过原点,并且在原点处与x轴相切。
当α为奇数时,图像关于原点对称;当α为偶数时,图像关于y轴对称。
2.幂函数的性质:函数。
定义域。
值域。
奇偶性。
单调性。
公共点y=x^2.R。
[0,+∞)。
偶。
增。
(0,0)y=x。
R。
R。
非奇非偶。
增。
(0,0)y=x^3.R。
R。
奇。
增。
(0,0)y=x^-1.{x|x≠0}。
{y|y≠0}。
奇。
(-∞,0)减。
(-1,0)∪(0,1)三、指数函数y=a^x(a>1且a≠1),定义域为R,为无界函数。
1.指数函数的图像:当a>1时,图像是单调增的曲线,经过点(0,1);当0<a<1时,图像是单调减的曲线,也经过点(0,1)。
2.指数函数的性质:函数。
定义域。
值域。
奇偶性。
单调性。
公共点y=a^x(a>1)。
R。
(0,+∞)。
非奇非偶。
增。
(0,1)y=a^x(0<a<1)。
R。
(0,1)。
非奇非偶。
减。
(0,1)本文介绍了指数函数和对数函数的基本概念和性质。
首先,介绍了指数函数的图像和比较大小的方法。
当底数互为倒数时,两个指数函数的图像关于y轴对称。
当底数大于1时,指数函数的值随着底数的增大而增大;当底数小于1时,指数函数的值随着底数的增大而减小。
其次,介绍了指数的运算法则,包括整数指数幂的运算性质和分数指数幂的运算性质。
其中,整数指数幂的运算性质包括指数相加、相减和相乘的规律;分数指数幂的运算性质包括分数指数幂的乘方和除法的规律。
接着,介绍了对数函数的概念和性质。
对数函数是指底数为常数且大于1的指数函数的反函数。
常用对数是以10为底的对数,自然对数是以无理数e为底的对数。
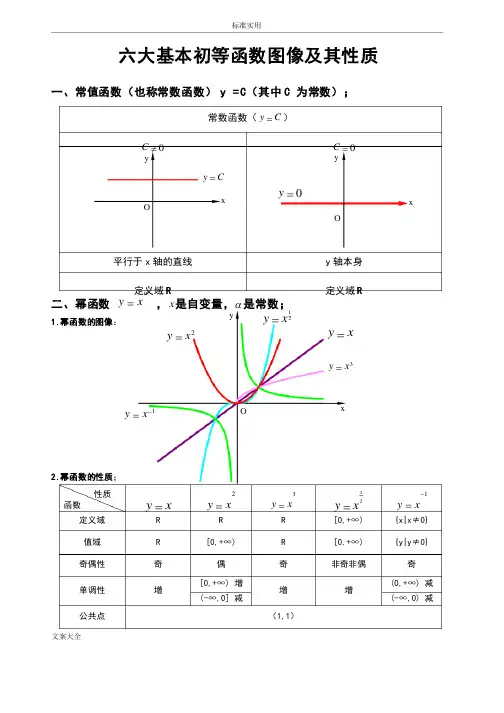
标准实用文案大全六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);常数函数(C y =)≠C 0=C 平行于x 轴的直线y 轴本身定义域R 定义域R二、幂函数αx y=,x 是自变量,α是常数;1.幂函数的图像:2.幂函数的性质;性质函数xy =2xy =3xy =21x y =1-=xy 定义域R R R [0,+[0,+∞∞) {x|x {x|x≠≠0} 值域R [0,+[0,+∞∞) R [0,+[0,+∞∞) {y|y {y|y≠≠0} 奇偶性奇偶奇非奇非偶奇单调性增[0,+[0,+∞∞) ) 增增增增(0,+(0,+∞∞) ) 减减(-(-∞∞,0] ,0] 减减(-(-∞∞,0) ,0) 减减公共点(1,11,1))xyOxy =2x y =3x y =1-=x y 21x y =O=y xCy =Oxyy1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α,他们的图形都经过原点,并当α>1>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm 时,时,n n 为偶数时函数的定义域为(为偶数时函数的定义域为(0, +0, +0, +∞),∞),∞),n n 为奇数时函数的定义域为(为奇数时函数的定义域为(--∞,+,+∞),函数的图形均经过原点和(∞),函数的图形均经过原点和(∞),函数的图形均经过原点和(1 ,11 ,11 ,1););4)如果m>n 图形于x 轴相切,如果m<n,m<n,图形于图形于y 轴相切,且m 为偶数时,还跟y 轴对称;轴对称;m m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,)当α为负有理数时,n n 为偶数时,函数的定义域为大于零的一切实数;为偶数时,函数的定义域为大于零的一切实数;n n 为奇数时,定义域为去除x=0以外的一切实数。
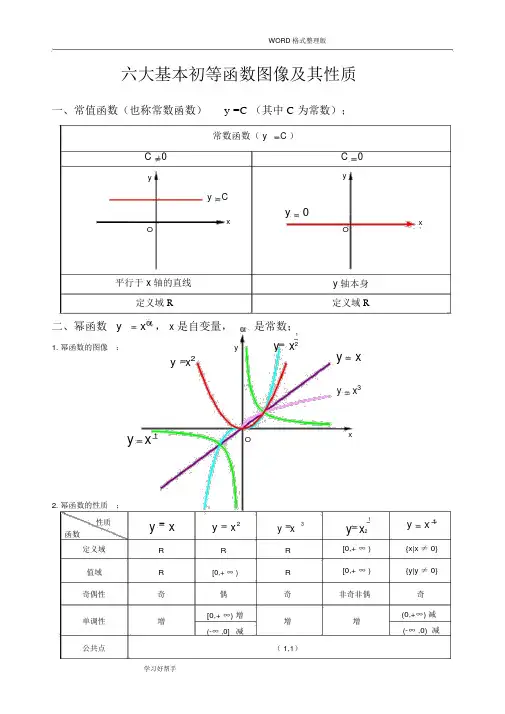
WORD 格式整理版六大基本初等函数图像及其性质一、常值函数(也称常数函数)y =C (其中 C 为常数);常数函数( y C )C 0yy Cy 0xO平行于 x 轴的直线定义域 R二、幂函数 y x ,x是自变量,是常数;y 11. 幂函数的图像:y x2y x2y x1O2.幂函数的性质;性质y x y x2y x3函数定义域R R R值域R[0,+ ∞ )R奇偶性奇偶奇单调性增[0,+ ∞) 增增(-∞ ,0]减公共点( 1,1)C 0yOy轴本身定义域 Ry xy x3x1y x2[0,+ ∞ )[0,+ ∞ )非奇非偶增xy x 1{x|x ≠ 0}{y|y ≠ 0}奇(0,+∞) 减(-∞ ,0) 减WORD 格式整理版1)当 α 为正整数时,函数的定义域为区间为x ( ,),他们的图形都经过原点,并当α >1 时在原点处与 x 轴相切。
且 α为奇数时,图形关于原点对称;α 为偶数时图形关于 y 轴对称;2)当 α 为负整数时。
函数的定义域为除去 x=0 的所有实数;3)当 α 为正有理数m时, n 为偶数时函数的定义域为(0, +∞), n 为奇数时函数的定义域为( -n∞ ,+∞),函数的图形均经过原点和( 1 ,1);4)如果 m>n 图形于 x 轴相切,如果m<n,图形于 y 轴相切,且 m 为偶数时,还跟y 轴对称; m , n均为奇数时,跟原点对称;5)当 α 为负有理数时, n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除 x=0 以外的一切实数。
三、指数函数 ya x ( x 是自变量 , a 是常数且 a0 , a 1) ,定义域是 R ;[ 无界函数 ]1. 指数函数的图象 :ya xyyya x(a 1)(0 a1)(0,1)y 1(0,1)y 1OxOx2. 指数函数的性质 ;性质y a x(a 1)y a x(0 a 1)函数定义域 R值域(0,+∞)奇偶性非奇非偶公共点过点 (0,1),即 x0 时, y 1单调性 在( ,)是增函数在(, )是减函数1 ) 当 a 1时 函 数 为 单 调 增 , 当 0 a 1时函数为单调减;2 ) 不 论 x 为 何 值 , y 总 是 正 的 , 图 形 在 x 轴 上 方 ;3 ) 当 x0 时 , y1,所以它的图形通过(0,1) 点。

知识归纳:1、 指数函数)1,0(≠>=a a a y x与对数函数)1,0(log ≠>=a a x y a 互为反函数,它们的图象关于直线x y =对称,其图象性质见下表:(1)定义:)1,,,0(1,>∈>==*-n N n m a aaa anm nm n m nm(2)运算性质:),,0,0()(,)(,Q t s b a b a ab a a a a a s s s st t s t s ts∈>>===⋅+3、对数定义及运算性质(1)定义:若)1,0(≠>=a a N a b,则数b 叫做以a 为底N 的对数,记作b N a =log(2)常用对数、自然对数对数)1,0(log ≠>a a N a 当底数10=a 时,叫常用对数,记作N lg ;当底数e a =时,叫自然对数,记作N ln(3)对数恒等式:)0,1,0(log >≠>=N a a N aNa (4)换底公式:)0,1,,0,(log log log >≠>=N b a b a aNN b b a (5)对数运算法则N M MN a a a log log )(log += )1,0,0,0(≠>>>a a N MN M NM b a a log log log -= )1,0,0,0(≠>>>a a N MN n N a n a log log = )1,0,0(≠>>a a NN n N a n a log 1log = )1,0,0(≠>>a a Nb n mb a m a n log log = )1,0,0,0(≠>>≠a a b nab b a log 1log = )1,0,1,0(≠>≠>a a b b考点1指数函数与对数函数的定义域、值域 例1.设2()lg 2x f x x +=-,则2()()2x f f x+的定义域为 A .(4,0)(0,4)- B .(4,1)(1,4)-- C .(2,1)(1,2)-- D .(4,2)(2,4)--考点2指数函数与对数函数的图像 例2.函数xe y -=的图象( ) A .与x e y =的图象关于y 轴对称 B .与xe y =的图象关于坐标原点对称C .与x ey -=的图象关于y 轴对称D .与xey -=的图象关于坐标原点对称例3.为了得到函数xy )31(3⨯=的图象,可以把函数xy )31(=的图象( ) A .向左平移3个单位长度 B .向右平移3个单位长度C .向左平移1个单位长度D .向右平移1个单位长度考点3由指数函数与对数函数的图像确定参数的值或范围例4.若函数)1,0)((log ≠>+=a a b x y a 的图象过两点(-1,0)和(0,1),则( ) A .a =2,b=2 B .a = 2 ,b=2 C .a =2,b=1 D .a = 2 ,b= 2例5.若直线y=2a 与函数y=|a x-1|(a >0,且a ≠1)的图象有两个公共点,则a 的取值范围是考点4指数函数与对数函数的互为反函数关系例6.记函数y=1+3-x的反函数为()y g x =,则g(10)=( )A . 2B . 2-C . 3D . 1-考点5指数方程与对数方程 例7.解方程 11214=-+xx .例8.(2006年上海文科卷第8题) 方程x x 323log 1)10(log +=-的解是 .考点6指数函数与对数函数的单调性例9.设()2log log ,2log ,3log 3232===R Q P ,则( )A.P Q R <<B.Q R P <<C.P R Q <<D.Q P R <<例10.求函数()()24log 23f x x x =+-的单调区间考点7求参数的取值范围例11、若()log 3a y ax =-在[]0,1上是x 的减函数,则a 的取值范围是( ) A 、()0,1 B 、()1,3 C 、()0,3 D 、[)3,+∞点评:由常规的具体函数判断单调性或求已知函数的单调区间,变换为由函数的单调性反过来确定函数中的底数a 的范围,同时要求对对数函数的概念和性质有深刻的理解。
一、一次函数二、二次函数(1)二次函数解析式的三种形式 ①一般式:2()(0)f x ax bx c a =++≠ ②顶点式:2()()(0)f x a x h k a =-+≠ ③两根式:12()()()(0)f x a x x x x a =--≠(2)求二次函数解析式的方法①已知三个点坐标时,宜用一般式.②已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式. ③若已知抛物线与x 轴有两个交点,且横线坐标已知时,选用两根式求()f x 更方便. (①.二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线,对称轴方程为,2x a=-顶点坐标是24(,)24b ac b a a-- ②当0a >时,抛物线开口向上,函数在(,]2b a -∞-上递减,在[,)2ba-+∞上递增,当2b x a =-时,2min 4()4ac b fx a -=;当0a <时,抛物线开口向下,函数在(,]2ba -∞-上递增,在[,)2ba-+∞上递减,当2b x a =-时,2max 4()4ac b f x a -=. 三、幂函数(1)幂函数的定义一般地,函数y x α=叫做幂函数,其中x 为自变量,α是常数. 过定点:所有的幂函数在(0,)+∞都有定义,并且图象都通过点(1,1).(1)根式的概念:如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根. (2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是:1()0,,,m m nn a a m n N a -+==>∈且1)n >.0的负分数指数幂没有意义. (3)运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈(1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数. ②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a a a M N MN += ②减法:log log log a a aM M N N-= ③数乘:log log ()na a n M M n R =∈ ④log a NaN =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且(5)对数函数(6)反函数的概念设函数()y f x =的定义域为A ,值域为C ,从式子()y f x =中解出x ,得式子()x y ϕ=.如果对于y 在C 中的任何一个值,通过式子()x y ϕ=,x 在A 中都有唯一确定的值和它对应,那么式子()x y ϕ=表示x 是y 的函数,函数()x y ϕ=叫做函数()y f x =的反函数,记作1()x fy -=,习惯上改写成1()y f x -=.(7)反函数的求法①确定反函数的定义域,即原函数的值域;②从原函数式()y f x =中反解出1()x f y -=;③将1()x fy -=改写成1()y f x -=,并注明反函数的定义域.(8)反函数的性质①原函数()y f x =与反函数1()y fx -=的图象关于直线y x =对称.②函数()y f x =的定义域、值域分别是其反函数1()y fx -=的值域、定义域.③若(,)P a b 在原函数()y f x =的图象上,则'(,)P b a 在反函数1()y f x -=的图象上.④一般地,函数()y f x =要有反函数则它必须为单调函数. 例题一、求二次函数的解析式例1.抛物线244y x x =--的顶点坐标是()A .(2,0)B .(2,-2)C .(2,-8)D .(-2,-8) 例2.已知抛物线的顶点为(1,2),且通过(1,10),则这条抛物线的表达式为()A .()2312y x =-- B .()2312y x =-+ C. ()2312y x =+- D.()2312y x =-+---例3.抛物线y=的顶点在第三象限,试确定m 的取值范围是( ) A .m <-1或m >2 B .m <0或m >-1 C .-1<m <0 D .m <-1例4.已知二次函数()f x 同时满足条件:(1)()()11f x f x +=-;(2)()f x 的最大值为15;(3)()0f x =的两根立方和等于17求()f x 的解析式二、二次函数在特定区间上的最值问题例5. 当22x -≤≤时,求函数223y x x =--的最大值和最小值.例6.当0x ≥时,求函数(2)y x x =--的取值范围.例7.当1t x t ≤≤+时,求函数21522y x x =--的最小值(其中t 为常数).222x mx m -++三、幂函数例8.下列函数在(),0-∞上为减函数的是()A.13y x = B.2y x = C.3y x = D.2y x -=例9.下列幂函数中定义域为{}0x x >的是() A.23y x = B.32y x = C.23y x-= D.32y x-=例10.讨论函数y =52x 的定义域、值域、奇偶性、单调性,并画出图象的示意图.例10.已知函数y =42215x x --.(1)求函数的定义域、值域;(2)判断函数的奇偶性; (3)求函数的单调区间.四、指数函数的运算例11.计算122(2)-⎡⎤-⎣⎦的结果是( ) A、12C、—12例12.等于( ) A 、 B 、C 、 D 、例13.若53,83==ba ,则b a233-=___________五、指数函数的性质例14.{|2},{|xM y y P y y ====,则M ∩P ()A.{|1}y y >B. {|1}y y ≥C. {|0}y y >D. {|0}y y ≥ 例15.求下列函数的定义域与值域: (1)442x y -=(2)||2()3x y =例16.函数()2301x y a a a -=+>≠且的图像必经过点 ( )A .(0,1)B .(1,1)C .(2,3)D .(2,4)例17求函数y=2121x x -+的定义域和值域,并讨论函数的单调性、奇偶性.4416a 8a 4a 2a五、对数函数的运算例18.已知32a=,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+ D 、23a a -例19.2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或1 例20.已知732log [log (log )]0x =,那么12x -等于( )A 、13B C D 例21.2log 13a <,则a 的取值范围是( ) A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞⎪⎝⎭C 、2,13⎛⎫ ⎪⎝⎭ D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭五、对数函数的性质例22.下列函数中,在()0,2上为增函数的是( )A 、12log (1)y x =+B 、2log y =C 、21log y x =D 、2log (45)y x x =-+ 例23.函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于( ) A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称例23.求证函数)()lg f x x =是(奇、偶)函数。
新高考数学复习考点知识专题讲义第2讲基本初等函数、函数与方程[考情分析]1.基本初等函数的图象、性质是高考考查的重点,利用函数性质比较大小是常见题型.2.函数零点的个数判断及参数范围是高考的热点,常以压轴题形式出现.考点一基本初等函数的图象与性质核心提炼1.指数函数y=a x(a>0,a≠1)与对数函数y=log a x(a>0,a≠1)互为反函数,其图象关于y=x对称,它们的图象和性质分0<a<1,a>1两种情况,着重关注两函数图象的异同.2.幂函数y=xα的图象和性质,主要掌握α=1,2,3,12,-1五种情况.例1(1)已知f(x)=2x-1,g(x)=1-x2,规定:当|f(x)|≥g(x)时,h(x)=|f(x)|;当|f(x)|<g(x)时,h(x)=-g(x),则h(x)()A.有最小值-1,最大值1B.有最大值1,无最小值C.有最小值-1,无最大值D.有最大值-1,无最小值答案C解析画出y=|f(x)|=|2x-1|与y=g(x)=1-x2的图象,它们交于A,B两点.由“规定”,在A ,B 两侧,|f (x )|≥g (x ),故h (x )=|f (x )|;在A ,B 之间,|f (x )|<g (x ),故h (x )=-g (x ).综上可知,y =h (x )的图象是图中的实线部分,因此h (x )有最小值-1,无最大值.(2)已知函数f (x )=e x +2(x <0)与g (x )=ln(x +a )+2的图象上存在关于y 轴对称的点,则a 的取值范围是()A.⎝ ⎛⎭⎪⎫-∞,1e B .(-∞,e) C.⎝ ⎛⎭⎪⎫-1e ,e D.⎝ ⎛⎭⎪⎫-e ,1e 答案B解析由题意知,方程f (-x )-g (x )=0在(0,+∞)上有解, 即e -x +2-ln(x +a )-2=0在(0,+∞)上有解,即函数y =e -x 与y =ln(x +a )的图象在(0,+∞)上有交点. 函数y =ln(x +a )可以看作由y =ln x 左右平移得到, 当a =0时,两函数有交点,当a <0时,向右平移,两函数总有交点,当a >0时,向左平移,由图可知,将函数y =ln x 的图象向左平移到过点(0,1)时,两函数的图象在(0,+∞)上不再有交点,把(0,1)代入y=ln(x+a),得1=ln a,即a=e,∴a<e.规律方法(1)对数函数与指数函数的单调性都取决于其底数的取值,当底数a的值不确定时,要注意分a>1和0<a<1两种情况讨论:当a>1时,两函数在定义域内都为增函数;当0<a<1时,两函数在定义域内都为减函数.(2)基本初等函数的图象和性质是统一的,在解题中可相互转化.跟踪演练1(1)函数f(x)=ln(x2+2)-e x-1的大致图象可能是()答案A解析当x→+∞时,f(x)→-∞,故排除D;函数f(x)的定义域为R,且在R上连续,故排除B;f(0)=ln2-e-1,由于ln2>ln e=12,e-1<12,所以f(0)=ln2-e-1>0,故排除C.(2)已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-2-x,则不等式f(x)<-1 2的解集是()A.(-∞,-1) B.(-∞,-1] C.(1,+∞) D.[1,+∞)答案A解析当x >0时,f (x )=1-2-x >0. 又f (x )是定义在R 上的奇函数,所以f (x )<-12的解集和f (x )>12的解集关于原点对称,由1-2-x >12得2-x <12=2-1, 即x >1,则f (x )<-12的解集是(-∞,-1).故选A.考点二函数的零点 核心提炼判断函数零点个数的方法: (1)利用零点存在性定理判断法. (2)代数法:求方程f (x )=0的实数根.(3)几何法:对于不易求根的方程,将它与函数y =f (x )的图象联系起来,利用函数的性质找出零点或利用两个函数图象的交点求解.在利用函数性质时,可用求导的方法判断函数的单调性.考向1函数零点的判断例2(1)(2022·长沙调研)已知函数f (x )=⎩⎨⎧x e x ,x ≤0,2-|x -1|,x >0,若函数g (x )=f (x )-m 有两个不同的零点x 1,x 2,则x 1+x 2等于()A.2B.2或2+1 eC.2或3D.2或3或2+1 e答案D解析当x≤0时,f′(x)=(x+1)e x,当x<-1时,f′(x)<0,故f(x)在(-∞,-1)上单调递减,当-1<x≤0时,f′(x)>0,故f(x)在(-1,0]上单调递增,所以x≤0时,f(x)的最小值为f(-1)=-1e.又当x≥1时,f(x)=3-x,当0<x<1时,f(x)=x+1.作出f(x)的图象,如图所示.因为g(x)=f(x)-m有两个不同的零点,所以方程f(x)=m 有两个不同的根,等价于直线y=m与f(x)的图象有两个不同的交点,且交点的横坐标分别为x1,x2,由图可知1<m<2或m=0或m=-1e.若1<m<2,则x1+x2=2;若m =0,则x 1+x 2=3;若m =-1e ,则x 1+x 2=-1+3+1e =2+1e .(2)设函数f (x )是定义在R 上的偶函数,且对任意的x ∈R ,都有f (x +2)=f (2-x ),当x ∈[-2,0]时,f (x )=⎝ ⎛⎭⎪⎫22x -1,则关于x 的方程f (x )-log 8(x +2)=0在区间(-2,6)上根的个数为()A .1B .2C .3D .4 答案C解析对于任意的x ∈R ,都有f (2+x )=f (2-x ), ∴f (x +4)=f [2+(x +2)]=f [2-(x +2)]=f (-x )=f (x ), ∴函数f (x )是一个周期函数,且T =4.又∵当x ∈[-2,0]时,f (x )=⎝ ⎛⎭⎪⎫22x -1,且函数f (x )是定义在R 上的偶函数,且f (6)=1,则函数y =f (x )与y =log 8(x +2)在区间(-2,6)上的图象如图所示,根据图象可得y =f (x )与y =log 8(x +2)在区间(-2,6)上有3个不同的交点,即f (x )-log 8(x +2)=0在区间(-2,6)上有3个根.考向2求参数的值或取值范围例3(1)已知关于x 的方程9-|x -2|-4·3-|x -2|-a =0有实数根,则实数a 的取值范围是________. 答案[-3,0)解析设t =3-|x -2|(0<t ≤1), 由题意知a =t 2-4t 在(0,1]上有解, 又t 2-4t =(t -2)2-4(0<t ≤1), ∴-3≤t 2-4t <0,∴实数a 的取值范围是[-3,0).(2)已知函数f (x )=⎩⎨⎧x +3,x >a ,x 2+6x +3,x ≤a ,若函数g (x )=f (x )-2x 恰有2个不同的零点,则实数a 的取值范围为____________________. 答案[-3,-1)∪[3,+∞)解析由题意得g (x )=⎩⎪⎨⎪⎧x +3-2x ,x >a ,x 2+6x +3-2x ,x ≤a ,即g (x )=⎩⎪⎨⎪⎧3-x ,x >a ,x 2+4x +3,x ≤a ,如图所示,因为g(x)恰有两个不同的零点,即g(x)的图象与x轴有两个交点.若当x≤a时,g(x)=x2+4x+3有两个零点,则令x2+4x+3=0,解得x=-3或x=-1,则当x>a时,g(x)=3-x没有零点,所以a≥3.若当x≤a时,g(x)=x2+4x+3有一个零点,则当x>a时,g(x)=3-x必有一个零点,即-3≤a<-1,综上所述,a∈[-3,-1)∪[3,+∞).规律方法利用函数零点的情况求参数值(或取值范围)的三种方法跟踪演练2(1)已知偶函数y=f(x)(x∈R)满足f(x)=x2-3x(x≥0),若函数g(x)=⎩⎪⎨⎪⎧log 2x ,x >0,-1x,x <0,则y =f (x )-g (x )的零点个数为()A .1B .3C .2D .4 答案B解析作出函数f (x )与g (x )的图象如图,由图象可知两个函数有3个不同的交点,所以函数y =f (x )-g (x )有3个零点.(2)(多选)已知函数f (x )=⎩⎨⎧x +2a ,x <0,x 2-ax ,x ≥0,若关于x 的方程f (f (x ))=0有8个不同的实根,则a 的值可能为() A .-6B .8C .9D .12 答案CD解析当a ≤0时,f (x )仅有一个零点x =0,故f (f (x ))=0有8个不同的实根不可能成立.当a >0时,f (x )的图象如图所示,当f (f (x ))=0时,f 1(x )=-2a ,f 2(x )=0,f 3(x )=a .又f (f (x ))=0有8个不同的实根,故f 1(x )=-2a 有三个根,f 2(x )=0有三个根,f 3(x )=a 有两个根,又x 2-ax =⎝ ⎛⎭⎪⎫x -a 22-a24,所以-2a >-a 24且a <2a ,解得a >8且a >0,综上可知,a >8.专题强化练一、单项选择题1.(2022·全国Ⅰ)设a log 34=2,则4-a 等于() A.116B.19C.18D.16 答案B解析方法一因为a log 34=2, 所以log 34a =2, 所以4a =32=9, 所以4-a =14a =19. 方法二因为a log 34=2,所以a =2log 34=2log 43=log 432=log 49,所以4-a =4log 94-=14log 94-=9-1=19.2.函数f (x )=ln x +2x -6的零点一定位于区间()A.(1,2) B.(2,3) C.(3,4) D.(4,5)答案B解析函数f(x)=ln x+2x-6在其定义域上连续且单调,f(2)=ln2+2×2-6=ln2-2<0,f(3)=ln3+2×3-6=ln3>0,故函数f(x)=ln x+2x-6的零点在区间(2,3)上.3.在同一直角坐标系中,函数f(x)=2-ax和g(x)=log a(x+2)(a>0且a≠1)的大致图象可能为()答案A解析由题意知,当a>0时,函数f(x)=2-ax为减函数.若0<a<1,则函数f(x)=2-ax的零点x0=2a∈(2,+∞),且函数g(x)=log a(x+2)在(-2,+∞)上为减函数;若a>1,则函数f(x)=2-ax的零点x0=2a∈(0,2),且函数g(x)=log a(x+2)在(-2,+∞)上为增函数.故A 正确.4.(2022·广东省揭阳三中模拟)已知a ,b ,c 满足4a =6,b =12log 4,c 3=35,则()A .a <b <cB .b <c <aC .c <a <bD .c <b <a 答案B解析4a =6>4,a >1,b =12log 4=-2,c 3=35<1,0<c <1,故a >c >b .5.(2022·全国Ⅲ)Logistic 模型是常用数学模型之一,可应用于流行病学领城.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位:天)的Logistic 模型:I (t )=K 1+e-0.23(t -53),其中K 为最大确诊病例数.当I (t *)=0.95K 时,标志着已初步遏制疫情,则t *约为(ln19≈3)() A .60B .63C .66D .69 答案C 解析因为I (t )=K1+e -0.23(t -53),所以当I (t *)=0.95K 时,*0.23531et K⎛⎫-- ⎪⎝⎭+=0.95K ,即*0.235311et ⎛⎫-- ⎪⎝⎭+=0.95,即1+*0.2353et ⎛⎫-- ⎪⎝⎭=10.95,即*0.2353et ⎛⎫-- ⎪⎝⎭=10.95-1,∴*0.2353et ⎛⎫- ⎪⎝⎭=19,∴0.23(t *-53)=ln19, ∴t *=ln190.23+53≈30.23+53≈66.6.(2022·泉州模拟)若函数y =log a (x 2-ax +1)有最小值,则a 的取值范围是() A .1<a <2B .0<a <2,a ≠1 C .0<a <1D .a ≥2 答案A解析令u (x )=x 2-ax +1,函数y =log a (x 2-ax +1)有最小值,∴a >1,且u (x )min >0,∴Δ=a 2-4<0,∴1<a <2,∴a 的取值范围是1<a <2.7.(2022·太原质检)已知函数f (x )=⎩⎨⎧e x ,x >0,-2x 2+4x +1,x ≤0(e 为自然对数的底数),若函数g (x )=f (x )+kx 恰好有两个零点,则实数k 等于() A .-2eB .eC .-eD .2e 答案C解析g (x )=f (x )+kx =0,即f (x )=-kx ,如图所示,画出函数y =f (x )和y =-kx 的图象, -2x 2+4x +1=-kx ,即2x 2-(4+k )x -1=0, 设方程的两根为x 1,x 2,则Δ=(4+k )2+8>0,且x 1x 2=-12, 故g (x )在x <0时有且仅有一个零点, y =-kx 与y =f (x )在x >0时相切.当x >0时,设切点为(x 0,-kx 0),f (x )=e x , f ′(x )=e x ,f ′(x 0)=0e x =-k ,0e x =-kx 0, 解得x 0=1,k =-e.8.已知函数f (x )=⎩⎪⎨⎪⎧a ,x =0,⎝ ⎛⎭⎪⎫1e |x |+1,x ≠0,若关于x 的方程2f 2(x )-(2a +3)f (x )+3a =0有五个不同的解,则a 的取值范围是() A .(1,2) B.⎣⎢⎡⎭⎪⎫32,2C.⎝ ⎛⎭⎪⎫1,32D.⎝ ⎛⎭⎪⎫1,32∪⎝ ⎛⎭⎪⎫32,2 答案D解析作出f (x )=⎝ ⎛⎭⎪⎫1e |x |+1,x ≠0的图象如图所示.设t =f (x ),则原方程化为2t 2-(2a +3)t +3a =0, 解得t 1=a ,t 2=32.由图象可知,若关于x 的方程2f 2(x )-(2a +3)f (x )+3a =0有五个不同的实数解,只有当直线y =a 与函数y =f (x )的图象有三个不同的交点时才满足条件, 所以1<a <2.又方程2t 2-(2a +3)t +3a =0有两个不相等的实数根, 所以Δ=(2a +3)2-4×2×3a =(2a -3)2>0, 解得a ≠32,综上,得1<a <2,且a ≠32. 二、多项选择题9.(2022·临沂模拟)若10a =4,10b =25,则() A .a +b =2B .b -a =1 C .ab >8lg 22D .b -a >lg6 答案ACD解析由10a =4,10b =25,得a =lg4,b =lg25,则a +b =lg4+lg25=lg100=2,故A 正确;b-a=lg25-lg4=lg 254>lg6且lg254<1,故B错误,D正确;ab=lg4·lg25=4lg2·lg5>4lg2·lg4=8lg22,故C正确.10.已知函数f(x)=log a(x+1),g(x)=log a(1-x),a>0,a≠1,则()A.函数f(x)+g(x)的定义域为(-1,1)B.函数f(x)+g(x)的图象关于y轴对称C.函数f(x)+g(x)在定义域上有最小值0D.函数f(x)-g(x)在区间(0,1)上是减函数答案AB解析∵f(x)=log a(x+1),g(x)=log a(1-x),a>0,a≠1,∴f(x)+g(x)=log a(x+1)+log a(1-x),由x+1>0且1-x>0得-1<x<1,故A对;由f(-x)+g(-x)=log a(-x+1)+log a(1+x)=f(x)+g(x),得函数f(x)+g(x)是偶函数,其图象关于y轴对称,B对;∵-1<x<1,∴f(x)+g(x)=log a(1-x2),∵y=1-x2在[0,1)上单调递减,由复合函数的单调性可知,当0<a<1时,函数f(x)+g(x)在[0,1)上单调递增,有最小值f(0)+g(0)=log a(1-0)=0;当a>1时,函数f(x)+g(x)在[0,1)上单调递减,无最小值,故C错;∵f(x)-g(x)=log a(x +1)-log a(1-x),当0<a<1时,f(x)=log a(x+1)在(0,1)上单调递减,g(x)=log a(1-x)在(0,1)上单调递增,函数f(x)-g(x)在(0,1)上单调递减;当a>1时,f(x)=log a(x+1)在(0,1)上单调递增,g(x)=log a(1-x)在(0,1)上单调递减,函数f(x)-g(x)在(0,1)上单调递增,故D错.11.(2022·淄博模拟)已知函数y =f (x )是R 上的奇函数,对于任意x ∈R ,都有f (x +4)=f (x )+f (2)成立.当x ∈[0,2)时,f (x )=2x -1.给出下列结论,其中正确的是() A .f (2)=0B .点(4,0)是函数y =f (x )图象的一个对称中心C .函数y =f (x )在区间[-6,-2]上单调递增D .函数y =f (x )在区间[-6,6]上有3个零点 答案AB解析对于A ,因为f (x )为奇函数且对任意x ∈R ,都有f (x +4)=f (x )+f (2),令x =-2,则f (2)=f (-2)+f (2)=0,故A 正确;对于B ,由A 知,f (2)=0,则f (x +4)=f (x ),则4为f (x )的一个周期,因为f (x )的图象关于原点(0,0)成中心对称,则(4,0)是函数f (x )图象的一个对称中心,故B 正确;对于C ,因为f (-6)=0,f (-5)=f (-5+4)=f (-1)=-f (1)=-1,-6<-5,而f (-6)>f (-5),所以f (x )在区间[-6,-2]上不是单调递增的,故C 错误;对于D ,因为f (0)=0,f (2)=0,所以f (-2)=0,又4为f (x )的一个周期,所以f (4)=0,f (6)=0,f (-4)=0,f (-6)=0,所以函数y =f (x )在区间[-6,6]上有7个零点,故D 错误. 12.对于函数f (x )=⎩⎪⎨⎪⎧sinπx ,x ∈[0,2],12f (x -2),x ∈(2,+∞),则下列结论正确的是()A .任取x 1,x 2∈[2,+∞),都有|f (x 1)-f (x 2)|≤1B .函数y =f (x )在[4,5]上单调递增C .函数y =f (x )-ln(x -1)有3个零点D .若关于x 的方程f (x )=m (m <0)恰有3个不同的实根x 1,x 2,x 3,则x 1+x 2+x 3=132 答案ACD解析f (x )=⎩⎨⎧sinπx ,x ∈[0,2],12f (x -2),x ∈(2,+∞)的图象如图所示,当x ∈[2,+∞)时,f (x )的最大值为12,最小值为-12,∴任取x 1,x 2∈[2,+∞),都有|f (x 1)-f (x 2)|≤1恒成立,故A 正确;函数y =f (x )在[4,5]上的单调性和在[0,1]上的单调性相同,则函数y =f (x )在[4,5]上不单调,故B 错误;作出y =ln(x -1)的图象,结合图象,易知y =ln(x -1)的图象与f (x )的图象有3个交点,∴函数y =f (x )-ln(x -1)有3个零点,故C 正确;若关于x 的方程f (x )=m (m <0)恰有3个不同的实根x 1,x 2,x 3,不妨设x 1<x 2<x 3,则x 1+x 2=3,x 3=72,∴x 1+x 2+x 3=132,故D 正确. 三、填空题13.(2022·全国Ⅱ)已知f (x )是奇函数,且当x <0时,f (x )=-e ax .若f (ln2)=8,则a =________. 答案-3解析当x >0时,-x <0,f (-x )=-e -ax .因为函数f (x )为奇函数,所以当x >0时,f (x )=-f (-x )=e -ax ,所以f (ln2)=e -a ln2=⎝⎛⎭⎪⎫12a=8,所以a =-3. 14.已知函数f (x )=|lg x |,若f (a )=f (b )(a ≠b ),则函数g (x )=⎩⎨⎧x 2+22x +5,x ≤0,ax 2+2bx ,x >0的最小值为________. 答案2 2解析因为|lg a |=|lg b |,所以不妨令a <b , 则有-lg a =lg b ,所以ab =1,b =1a(0<a <1),所以g (x )=⎩⎨⎧(x +2)2+3,x ≤0,ax +2ax ,x >0,当x ≤0时,g (x )=(x +2)2+3≥3,取等号时x =-2; 当x >0时,g (x )=ax +2ax ≥2ax ·2ax =22,当且仅当x =2a 时,等号成立, 综上可知,g (x )min =2 2.15.定义在R 上的奇函数f (x ),当x ≥0时,f (x )=⎩⎪⎨⎪⎧-2x x +1,x ∈[0,1),1-|x -3|,x ∈[1,+∞),则函数F (x )=f (x )-1π的所有零点之和为________.答案11-2π解析由题意知,当x <0时, f (x )=⎩⎪⎨⎪⎧-2x 1-x ,x ∈(-1,0),|x +3|-1,x ∈(-∞,-1],作出函数f (x )的图象如图所示,设函数y =f (x )的图象与y =1π交点的横坐标从左到右依次为x 1,x 2,x 3,x 4,x 5,由图象的对称性可知,x 1+x 2=-6,x 4+x 5=6,x 1+x 2+x 4+x 5=0,令-2x 1-x =1π,解得x 3=11-2π,所以函数F (x )=f (x )-1π的所有零点之和为11-2π. 16.对于函数f (x )与g (x ),若存在λ∈{x ∈R |f (x )=0},μ∈{x ∈R |g (x )=0},使得|λ-μ|≤1,则称函数f (x )与g (x )互为“零点密切函数”,现已知函数f (x )=e x -2+x -3与g (x )=x 2-ax -x +4互为“零点密切函数”,则实数a 的取值范围是________. 答案[3,4]解析由题意知,函数f (x )的零点为x =2, 设g (x )的零点为μ,满足|2-μ|≤1, 因为|2-μ|≤1,所以1≤μ≤3.21 / 21 方法一因为函数g (x )的图象开口向上,所以要使g (x )的至少一个零点落在区间[1,3]上,则需满足g (1)g (3)≤0,或⎩⎪⎨⎪⎧ g (1)>0,g (3)>0,Δ≥0,1<a +12<3,解得103≤a ≤4,或3≤a <103,得3≤a ≤4. 故实数a 的取值范围为[3,4].方法二因为g (μ)=μ2-aμ-μ+4=0, a =μ2-μ+4μ=μ+4μ-1,因为1≤μ≤3,所以3≤a ≤4.故实数a 的取值范围为[3,4].。
基本初等函数讲义(全)一、一次函数一次函数可以表示为y=kx+b(k不等于0),其中k表示斜率,b表示截距。
当k大于0时,函数图像随着x的增大而增大,当k小于0时,函数图像随着x的增大而减小。
当b大于0时,函数图像在y轴上方,当b小于0时,函数图像在y轴下方。
当b等于0时,函数图像经过原点。
二、二次函数1)二次函数有三种解析式形式:一般式、顶点式和两根式。
一般式为f(x)=ax^2+bx+c(a不等于0),顶点式为f(x)=a(x-h)^2+k(a不等于0),两根式为f(x)=a(x-x1)(x-x2)(a不等于0)。
2)求二次函数解析式的方法有三种情况:已知三个点坐标时,宜用一般式;已知抛物线的顶点坐标或与对称轴有关或与最大(小)值有关时,常使用顶点式;若已知抛物线与x轴有两个交点,且横线坐标已知时,选用两根式求f(x)更方便。
3)二次函数的图像是一条抛物线,对称轴方程为x=-b/2a,顶点坐标为(-b/2a。
-Δ/4a)。
当a大于0时,抛物线开口向上,函数在(-∞。
-b/2a)上递增,在[-b/2a。
+∞)上递减,最小值为f(-b/2a);当a小于0时,抛物线开口向下,函数在(-∞。
-b/2a]上递增,在[-b/2a。
+∞)上递减,最大值为f(-b/2a)。
三、幂函数1)幂函数可以表示为y=x^α,其中x为自变量,α是常数。
2)所有的幂函数在(0.+∞)都有定义,并且图像都通过点(1,1)。
四、指数函数1)根式的概念是指,如果xn=a,a属于实数,x属于实数,n大于1,且n属于正整数,那么x叫做a的n次方根。
2)正数的正分数指数幂的意义是,a的n次方根的正分数指数幂等于a的n次方。
正数的负分数指数幂没有意义。
非奇非偶函数指的是在定义域为(0.+∞)上的减函数。
对于loga x,当x>1时,函数值递增;当x<1时,函数值递减;当x=1时,函数值为0.在第一象限内,a越大,函数图像越靠低;在第四象限内,a越大,函数图像越靠高。
精心整理
函数图像+反函数+基本初等函数
一、函数图像:注意数形结合
(1)平移:−−−−−−→−=个单位向右平移a x f y )()(a x f y -=;)(x f y =−−−−−−→−个单位向上平移b .)(b x f y +=
(2)对称:)(x f y =−−−−−→−轴对称关于
x )(x f y -=;)(x f y =−−−−−→−轴对称关于y )(x f y -=; )(x f y =−−−−−→−关于原点对称
)(x f y --=. *若有等式)()(x a f x a f -=+成立,那么函数关于a x =对称; *若有等式)()(a x f a x f -=+成立,那么函数是周期函数,且周期为a 2
(3)其他:)(x f y =−−−−−−−−→−再把轴上方图象保留
,x |)(|x f y =;)(x f y =−−−−−−−−−→−再把轴右边的图象保留,x |).(|x f y = 习题1.例3、利用函数x x f 2)(=的图象,作出下列各函数的图象:
(1))1(-x f ;(2)|)(|x f ;(3)1)(-x f ;(4))(x f -;(5).|1)(|-x f
习题2.函数1
11--=x y 的图象是(B ) 习题3.已知)(x f 是偶函数,则)2(+x f 的图像关于__2x =-____对称;已知)2(+x f 是偶函数,则函数)(x f 的图像关于____2x =_____对称.
二、反函数
(1)互为反函数的两个函数y =f (x )与y =f -1(x )在同一直角坐标系中的图象关于直线y =x 对称.
(2)原函数与反函数有相同的增减性
(3)求反函数的步骤:
(a )解关于x 的方程y =f (x ),得到x =f -1(y ).
(b )把第一步得到的式子中的x 、y 对换位置,得到y =f -1(x ).
(c )求出并说明反函数的定义域〔即函数y =f (x )的值域〕.
习题4.函数y =-1
1+x (x ≠-1)的反函数是(A ) A.y =-x 1-1(x ≠0)B.y =-x 1+1(x ≠0)C.y =-x +1(x ∈R ) D.y =-x -1(x ∈R )
轴下方图象对称到上方x 轴左边
轴右边图象对称到y y
习题5..函数y =log 2(x +1)+1(x >0)的反函数为(A )
A.y =2x -1-1(x >1)
B.y =2x -1+1(x >1)
C.y =2x +1-1(x >0)
D.y =2x +1+1(x >0)
习题6.函数f (x )=-12+x (x ≥-2
1)的反函数(D ) A.在[-21,+∞)上为增函数 B.在[-2
1,+∞)上为减函数 C.在(-∞,0]上为增函数
D.在(-∞,0]上为减函数
习题7.设函数f (x )是函数g (x )=
x 21的反函数,则f (4-x 2)的单调递增区间为(C )
A.[0,+∞)
B.(-∞,0]
C.[0,2)
D.(-2,0] 习题8.求函数f (x )=⎩⎨⎧->+-≤+)
1(1),1(12x x x x 的反函数
习题9.求函数x a y =的反函数
三、基本初等函数
(1)指数函数:)1,0(≠>=a a a y x 且
a.定义域:R x ∈,
b.函数的值域为),0(+∞;
c.当10<<a 时函数为减函数,当1>a 时函数为增函数,
d.过定点(0,1)
e.0<c<d<1<a<b
指数函数运算法则:
①(0,,)r s r s a a a a r s R +⋅=>∈
②()(0,,)r s rs a a a r s R =>∈
③()(0,0,)r r r ab a b a b r R =>>∈
(2)对数函数:)1,0(log ≠>=a a x y a 且
a.定义域:),0(+∞
b.函数的值域为R ;
c.当10<<a 时函数为减函数,当1>a 时函数为增函数;
d.过定点(1,0)
e.0<c3<c4<1<<c2<c1
对数函数运算法则:如果a>0且a ≠1,M>0,N>0,那么
(3)幂函数:()a f x x =,定义域根据特定的a 值来确定。
习题
45
(3习题习题习题习题习题15.若{|2},{|x M y y P y y ====,则M∩P (C )
A.{|1}y y >
B.{|1}y y ≥
C.{|0}y y >
D.{|0}y y ≥
习题16.对数式2log (5)a b a -=-中,实数a 的取值范围是( C )
A.a>5,或a<2
B.2<a<5
C.2<a<3,或3<a<5
D.3<a<4
习题17.已知x a x f -=)()10(≠>a a 且,且)3()2(->-f f ,则a 的取值范围是(D )
A.0>a
B.1>a
C.1<a
D.10<<a
习题18.函数|log |)(2
1x x f =的单调递增区间是(D)
A 、]
1,0(B 、]1,0(C 、(0,+∞)D 、),1[+∞ 习题l y =A C 习题习题习题习题习题习题8100
习题26.函数2)23x (lg )x (f +-=恒过定点
习题27.点(2,1)与(1,2)在函数()2ax b f x +=的图象上,求()f x 的解析式:()22x f x -+= 习题28.已知()2x f x =,()g x 是一次函数,并且点(2,2)在函数[()]f g x 的图象上,点(2,5)在函数[()]g f x 的图象上,求()g x 的解析式.:()23g x x =- 习题29.已知函数x
x x f -+=11lg
)(,(1)求)(x f 的定义域;(2)使0)(>x f 的x 的取值范围. x
(1)(-1,1),(2)(0,1)
习题30.已知定义域为R 的函数12()22
x x b f x +-+=+是奇函数。
(Ⅰ)求b 的值; (Ⅱ)判断函数()f x 的单调性;(减函数)。