数学人教版八年级上册轴对称将军饮马问题

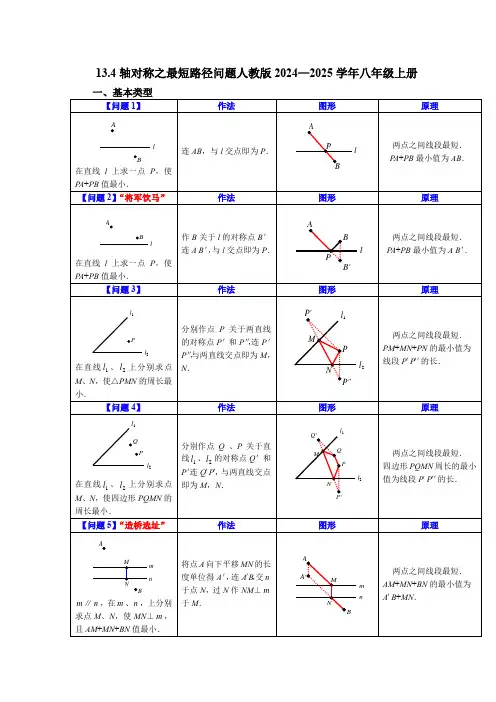
难关必刷03轴对称之将军饮马模型（3种类型30题专练）【模型梳理】如图，将军在图中点A处，现在他要带马去河边喝水，之后返回军营，问：将军怎么走能使得路程最短？B军营河如图，在直线上找一点P使得PA+PB最小？这个问题的难点在于PA+PB是一段折线段，通过观察图形很难得出结果，关于最小值，我们知道“两点之间，线段最短”、“点到直线的连线中，垂线段最短”等，所以此处，需转化问题，将折线段变为直线段．【模型解析】作点A关于直线的对称点A’，连接PA’，则PA’=PA，所以PA+PB=PA’+PB当A’、P、B三点共线的时候，PA’+PB=A’B，此时为最小值（两点之间线段最短）类型一：两定一动在OA 、OB 上分别取点M 、N ，使得△PMN 周长最小．此处M 、N 均为折点，分别作点P 关于OA （折点M 所在直线）、OB （折点N 所在直线）的对称点，化折线段PM +MN +NP 为P ’M +MN +NP ’’，当P ’、M 、N 、P ’’共线时，△PMN 周长最小．类型二：两定两动在OA 、OB 上分别取点M 、N 使得四边形PMNQ 的周长最小。

考虑PQ 是条定线段，故只需考虑PM +MN +NQ 最小值即可，类似，分别作点P 、Q 关于OA 、OB 对称，化折线段PM +MN +NQ 为P ’M +MN +NQ ’，当P ’、M 、N 、Q ’共线时，四边形PMNQ 的周长最小。

类型三：一定两动在OA 、OB 上分别取M 、N 使得PM +MN 最小。

此处M 点为折点，作点P 关于OA 对称的点P ’，将折线段PM +MN 转化为P ’M +MN ，即过点P ’作OB 垂线分别交OA 、OB 于点M 、N ，得PM +MN 最小值（点到直线的连线中，垂线段最短）BBBBBB【题型讲解】 类型一：两定一动 【例1】如图，在中，，是的两条中线，是上一个动点，则下列线段的长度等于最小值的是（ ）A ．B ．C ．D ．【变式】如图，点P 是∠AOB 内任意一点，∠AOB =30°，OP =8，点M 和点N 分别是射线OA 和射线OB 上的动点，则△PMN 周长的最小值为___________．类型二：两定两动【例2】如图，在Rt △ABC 中，∠ACB =90°，AC =6．AB =12，AD 平分∠CAB ，点F 是AC 的中点，点E 是AD 上的动点，则CE +EF 的最小值为A ．3B ．4C ．D ．【变式】如图，在锐角三角形ABC中，BC =4，∠ABC =60°， BD 平分∠ABC ，交AC 于点D ，M 、N 分别是BD ，BC 上的动点，则CM +MN 的最小值是P OBAMN()E AFCDB()AB ．2C ．D ．4类型三：一定两动【例3】点P 是定点，在OA 、OB 上分别取M 、N ，使得PM+MN 最小。

13.4轴对称之最短路径问题人教版2024—2025学年八年级上册二、例题讲解例1.如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC，已知线段AB＝4，DE＝2，BD＝8，设CD＝x．（1）用含x的代数式表示AC+CE的长；（2）请问点C满足什么条件时，AC+CE最小？最小为多少？（3）根据（2）中的规律和结论，请构图求代数式的最小值．变式1.如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，ED⊥BD，连结AC，EC，已知AB＝5，DE＝1，BD＝8．（1）请问点C什么位置时AC+CE的值最小？最小值为多少？（2）设BC＝x，则AC+CE可表示为，请直接写出的最小值为．例2.如图，直线l是一条河，P，Q是两个村庄，欲在l上的某处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）A．B．C．D．变式1.如图，在⊥ABC中，BA＝BC，BD平分⊥ABC，交AC于点D，点M、N 分别为BD、BC上的动点，若BC＝10，⊥ABC的面积为40，则CM+MN的最小值为．变式2.如图，等腰三角形ABC的底边BC长为8，面积是24，腰AC的垂直平分线EF分别交AC，AB于E，F点，若点D为BC边的中点，点M为线段EF 上一动点，则⊥CDM的周长的最小值为（）A．7B．8C．9D．10变式3.如图，在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点．（1）点D的坐标为；（2）若E为边OA上的一个动点，当⊥CDE的周长最小时，求点E的坐标．例3.如图，⊥AOB内一点P，P1，P2分别是P关于OA、OB的对称点，P1P2交OA于点M，交OB于点N．若⊥PMN的周长是6cm，则P1P2的长为（）A．6cm B．5cm C．4cm D．3cm变式1.已知点P在⊥MON内．如图1，点P关于射线OM的对称点是G，点P 关于射线ON的对称点是H，连接OG、OH、OP．（1）若⊥MON＝50°，求⊥GOH的度数；（2）如图2，若OP＝6，当⊥P AB的周长最小值为6时，求⊥MON的度数．变式2.如图，⊥MON＝45°，P为⊥MON内一点，A为OM上一点，B为ON上一点，当⊥P AB的周长取最小值时，⊥APB的度数为（）A．45°B．90°C．100°D．135°变式3.如图，⊥AOB＝30°，P是⊥AOB内的一个定点，OP＝12cm，C，D分别是OA，OB上的动点，连接CP，DP，CD，则⊥CPD周长的最小值为．变式4.如图，在五边形中，⊥BAE＝140°，⊥B＝⊥E＝90°，在边BC，DE上分别找一点M，N，连接AM，AN，MN，则当⊥AMN的周长最小时，求⊥AMN+⊥ANM 的值是（）A．100°B．140°C．120°D．80°例4.如图，在⊥ABC中，AB＝AC，⊥A＝90°，点D，E是边AB上的两个定点，点M，N分别是边AC，BC上的两个动点．当四边形DEMN的周长最小时，⊥DNM+⊥EMN的大小是（）A．45°B．90°C．75°D．135°变式1.如图，在平面直角坐标系中，已知点A（0，1），B（4，0），C（m+2，2），D（m，2），当四边形ABCD的周长最小时，m的值是（）A．B．C．1D．变式2.如图，在四边形ABCD中，⊥B＝90°，AB⊥CD，BC＝3，DC＝4，点E 在BC上，且BE＝1，F，G为边AB上的两个动点，且FG＝1，则四边形DGFE 的周长的最小值为．例5.如图，⊥AOB＝20°，点M、N分别是边OA、OB上的定点，点P、Q分别是边OB、OA上的动点，记⊥MPQ＝α，⊥PQN＝β，当MP+PQ+QN最小时，则β﹣α的值为（）A．10°B．20°C．40°D．60°变式1.如图，∠AOB＝20°，M，N分别为OA，OB上的点，OM＝ON＝3，P，Q分别为OA，OB上的动点，求MQ+PQ+PN的最小值。

八年级数学将军饮马最值问题分类总结轴对称的作用是“搬点移线”，可以把图形中比较分散、缺乏联系的元素集中到“新的图形”中，为应用某些基本定理提供方便。

比如我们可以利用轴对称性质求几何图形中一些线段和的最大值或最小值问题。

利用轴对称的性质解决几何图形中的最值问题借助的主要基本定理有三个：（1）两点之间线段最短；（2）三角形两边之和大于第三边；（3）垂线段最短。

初中阶段利用轴对称性质求最值的题目可以归结为：两点一线，两点两线，一点两线三类线段和的最值问题。

下面对三类线段和的最值问题进行分析、讨论。

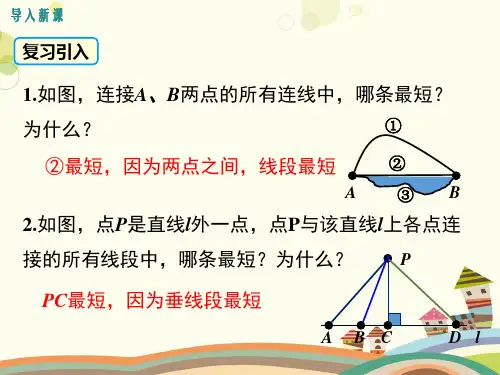
问题特征：已知两个定点位于一条直线的同一侧，在直线上求一动点的位置，使动点与定点线段和最短。

核心思路：这类最值问题所求的线段和中只有一个动点，解决这类题目的方法是找出任一定点关于直线的对称点，连结这个对称点与另一定点，交直线于一点，交点即为动点满足最值的位置。

方法：1.定点过动点所在直线做对称。

2.连结对称点与另一个定点，则直线段长度就是我们所求。

变异类型:实际考题中，经常利用本身就具有对称性质的图形，比如等腰三角形，等边三角形、正方形、圆、二次函数、直角梯形等图形，即其中一个定点的对称点就在这个图形上。

1.如图，直线l和l的同侧两点A、B，在直线l上求作一点P，使PA+PB最小。

（2）一点两线的最值问题：（两个动点+ 一个定点）问题特征：已知一个定点位于平面内两相交直线之间，分别在两直线上确定两个动点使线段和最短。

核心思路：这类问题实际上是两点两线段最值问题的变式，通过做这一定点关于两条线的对称点，实现“搬点移线”，把线段“移”到同一直线上来解决。

变异类型1.如图，点P是N MON内的一点，分别在OM, ON上作点A, B。

使C PAB的周长最小。

2.如图，点A是N MON外的一点，在射线OM上作点P,使PA与点P到射线ON的距离之和最小。

（3）两点两线的最值问题：（两个动点+两个定点）问题特征:两动点，其中一个随另一个动（一个主动，一个从动），并且两动点间的距离保持不变。

专题13.10最短路径（将军饮马）问题（知识梳理与考点分类讲解）第一部分【知识点归纳】【模型一：两定交点型】如图1，直线l和l的异侧两点A.B，在直线l上求作一点P，使PA+PB 最小；图1【模型二：两定一动型】如图2，直线l和l的同侧两点A.B，在直线l上求作一点P，使PA+PB 最小（同侧转化为异侧）；图2【模型三：一定两动型】如图3，点P是∠MON内的一点，分别在OM，ON上作点A，B。

使△PAB的周长最小。

图3【模型四：两定两动型】如图4，点P，Q为∠MON内的两点，分别在OM，ON上作点A，B。

使四边形PAQB的周长最小。

图4【模型五：一定两动（垂线段最短）型】如图5，点A是∠MON外的一点，在射线ON上作点P，使PA与点P到射线OM的距离之和最小。

图5【模型六：一定两动，找（作）对称点转化型】如图6，点A是∠MON内的一点，在射线ON 上作点P，使PA与点P到射线OM的距离之和最小。

图6【考点1】两定一动型；【考点2】一定两动（两点之间线段最短）型；【考点3】一定两动（垂线段最短）型；【考点4】两定两动型；【考点5】一定两动（等线段）转化型；.第二部分【题型展示与方法点拨】【考点1】两定一动型；【例1】（23-24八年级上·全国·课后作业）如图，在ABC ∆中，3,4AB AC ==，EF 垂直平分BC ，交AC 于点D ，则ABP 周长的最小值是（）A ．12B ．6C ．7D ．8【答案】C 【分析】本题主要考查了，轴对称﹣最短路线问题的应用，解此题的关键是找出P 的位置．凡是涉及最短距离的问题，一般要考虑线段的性质定理，结合轴对称变换来解决，根据题意知点B 关于直线EF 的对称点为点C ，故当点P 与点D 重合时，AP BP +的值最小，即可得到ABP 周长最小．解：∵EF 垂直平分BC ，∴点B ，C 关于EF 对称．∴当点P 和点D 重合时，AP BP +的值最小．此时AP BP AC +=，∵3,4AB AC ==，ABP ∴ 周长的最小值是347AP BP AB AB AC ++=+=+=，故选：C ．【变式】（23-24八年级上·广东广州·期中）如图，在ABC V 中，1216AB AC ==，，20BC =．将ABC V 沿射线BM 折叠，使点A 与BC 边上的点D 重合，E 为射线BM 上的一个动点，则CDE 周长的最小值．【答案】24【详解】设BM 与AC 的交点为点F ，连接AE ，DF 先根据折叠的性质可得12BD AB ==，DF AF =，DE AE =，BDF BAF ∠=∠，再根据两点之间线段最短可得当点E 与点F 重合时，CDE 周长最小，进而求解即可．解：如图，设BM 与AC 的交点为点F ，连接AE ，DF ，由折叠的性质得：12BD AB ==，DF AF =，DE AE =，BDF BAF ∠=∠，20128CD BC BD ∴=-=-=，CDE ∴ 周长8CD DE CE AE CE =++=++，要使CDE 周长最小，只需AE CE +最小，由两点之间线段最短可知，当点E 与点F 重合时，最小值为AC ，∴CDE 周长为：681624AC +=+=．故答案为：24．【点拨】本题考查了折叠的性质等知识点，熟练掌握折叠的性质是解题关键．【考点2】一定两动（两点之间线段最短）型；【例2】（23-24八年级上·湖北省直辖县级单位·期末）如图，45MON ∠=︒，P 为MON ∠内一点，A 为OM 上一点，B 为ON 上一点，当PAB 的周长取最小值时，APB ∠的度数为（）A ．45︒B ．90︒C ．100︒D ．135︒【答案】B 【分析】本题主要考查了最短路线问题、四边形的内角和定理、轴对称的性质等知识点，掌握两点之间线段最短的知识画出图形是解题的关键．如图：作P 点关于OM ON 、的对称点A B ''、，连接A B ''，此时PAB 的周长最小为A B ''，求出A B ''即可．解：如图：作P 点关于OM ON 、的对称点A B ''、，然后连接A B ''，∵点A '与点P 关于直线OM 对称，点B '与点P 关于ON 对称，∴A P OM B P ON A A AP B B BP ''''⊥⊥==，，，，∴A APA B BPB ''''∠=∠∠=∠，，∵A P OM B P ON ''⊥⊥，，∴180MON A PB ''∠+∠=︒，∴18045135A PB ''∠=︒-︒=︒，在A B P ''△中，由三角形的内角和定理可知：18013545A B ''∠+∠=︒-︒=︒，∴45A PA BPB ''∠+∠=︒，∴1354590APB ∠=︒-︒=︒．故选：B ．【变式】（23-24八年级上·江苏无锡·期中）如图，45AOB ∠=︒，点M N 、分别在射线OA OB 、上，5MN =，15OMN S = ，点P 是直线MN 上的一个动点，点P 关于OA 的对称点为1P ，点P 关于OB 的对称点为2P ，连接1OP 、2OP 、12PP ，当点P 在直线MN 上运动时，则12OPP 面积的最小值是．【考点3】一定两动型（垂线段最短）；【例3】（22-23八年级上·湖北武汉·期末）如图，在ABC V 中，3AB =，4BC =，5AC =，AB BC ⊥，点P 、Q 分别是边BC 、AC 上的动点，则AP PQ +的最小值等于（）A ．4B ．245C ．5D ．275【答案】B 【分析】作A 过于BC 的对称点A '，过点A '作A Q AC '⊥，交AC 于点Q ，交BC 于点P ，根据对称可得：AP PQ A P PQ A Q ''+=+≥，得到当,,A P Q '三点共线时，AP PQ +最小，再根据垂线段最短，得到A Q AC '⊥时，A Q '最小，进行求解即可．解：作A 过于BC 的对称点A '，过点A '作A Q AC '⊥，交AC 于点Q ，交BC 于点P ，【变式】（23-24七年级下·陕西西安·阶段练习）如图，在Rt ABC △中，90ACB ∠=︒，3AC =，4BC =，5AB =，AD 是ABC V 的角平分线，若P Q 、分别是AD 和AC 边上的动点，则PC PQ +的最小值是．AD 是BAC ∠的平分线，1QAD Q AD∴∠=∠在AQD 与1AQ D 中【考点4】两定两动型；【例4】如图，已知24AOB ∠=︒，OP 平分AOB ∠，1OP =，C 在OA 上，D 在OB 上，E 在OP 上．当CP CD DE ++取最小值时，此时PCD ∠的度数为（）A ．36︒B ．48︒C ．60︒D ．72︒【答案】D 【分析】作点P 关于OA 的对称点P'，作点E 关于OB 的对称点'E ，连接'OP 、'PP 、'OE 、'EE 、''P E ，则由轴对称知识可知=''CP CD DE CP CD DE ++++，所以依据垂线段最短知：当''P C D E 、、、在一条直线上，且'''P E OE ⊥时，CP CD DE ++取最小值，根据直角三角形的两锐角互余及三角形外角的性质可以'P C PC =，'E D ED =，'1OP OP ==，=''CP CD DE CP CD DE ++++，'P OE ∠''P C D E 、、、在一条直线上，且''P E ''=9048=42OP E ∠︒-︒︒，'='''=7842CP P OP P OP E ∠∠-∠︒-︒=【答案】44βα-=︒【分析】本题考查轴对称—最短问题、三角形的内角和定理．三角形的外角的性质等知识，解题的关键是灵活运用所学知识解决问题．OQM OQM NQP '∴∠=∠=∠，OPQ ∠∴1(180)2PQN AOB α∠=︒-=∠+∠44βα∴-=︒，故答案为：44βα-=︒．【考点5】一定两动（等线段）转化型；【例5】（20-21八年级上·湖北鄂州·期中）如图，AD 为等腰△ABC 的高，其中∠ACB =50°，AC =BC ，E ，F 分别为线段AD ，AC 上的动点，且AE =CF ，当BF ＋CE 取最小值时，∠AFB 的度数为（）A ．75°B ．90°C ．95°D ．105°【答案】C 【分析】先构造△CFH 全等于△AEC ，得到△BCH 是等腰直角三角形且FH=CE ，当FH+BF 最小时，即是BF+CE 最小时，此时求出∠AFB 的度数即可．解：如图，作CH ⊥BC ，且CH=BC ，连接HB ，交AC 于F ，此时△BCH 是等腰直角三角形且FH+BF 最小，∵AC=BC ，∴CH=AC ，∵∠HCB=90°，AD ⊥BC ，∴AD//CH ，∵∠ACB=50°，∴∠ACH=∠CAE=40°，∴△CFH ≌△AEC ，∴FH=CE ，∴FH+BF=CE+BF 最小，此时∠AFB=∠ACB+∠HBC=50°+45°=95°．故选：C ．【点拨】本题考查全等三角形的性质和判定、等腰三角形的性质、最短路径问题，关键是作出辅助线，有一定难度．【变式】（23-24七年级下·四川宜宾·期末）在ABC V 中，80CAB ∠=︒，2AB =，3AC =，点E 是边AB 的中点，CAB ∠的角平分线交BC 于点D ．作直线AD ，在直线AD 上有一点P ，连结PC 、PE ，则PC PE -的最大值是．∵CAB ∠的角平分线交∴FAP ∠∠=∵AP AP =，∴APF APE ≌∴PF PE =，第三部分【中考链接与拓展延伸】1、直通中考【例1】（2020·湖北·中考真题）如图，D 是等边三角形ABC 外一点．若8,6BD CD ==，连接AD ，则AD 的最大值与最小值的差为．【答案】12【分析】以CD 为边向外作等边三角形CDE ，连接BE ，可证得△ECB ≌△DCA 从而得到BE=AD ，再根据三角形的三边关系即可得出结论．解：如图1，以CD 为边向外作等边三角形CDE ，连接BE ，∵CE=CD ，CB=CA ，∠ECD=∠BCA=60°，∴∠ECB=∠DCA ，∴△ECB ≌△DCA （SAS ），∴BE=AD ，∵DE=CD=6，BD=8，∴8-6<BE<8+6，∴2<BE<14，∴2<AD<14．∴则AD 的最大值与最小值的差为12．故答案为：12【点拨】本题考查三角形全等与三角形的三边关系，解题关键在于添加辅助线构建全等三角形把AD 转化为BE 从而求解，是一道较好的中考题．【例2】（2020·新疆·中考真题）如图，在ABC V 中，90,60,4A B AB ∠=∠=︒=︒，若D 是BC 边上的动点，则2AD DC +的最小值为．在Rt DFC △中，30DCF ∠=︒，12DF DC ∴=，122()2AD DC AD DC +=+2()AD DF =+，∴当A ，D ，F 在同一直线上，即此时，60B ADB ∠=∠=︒，2、拓展延伸【例1】（23-24八年级上·江苏镇江·阶段练习）如图，AC 、BD 在AB 的同侧，点M 为线段AB 中点，2AC =，8BD =，8AB =，若120CMD ∠=︒，则CD 的最大值为（）A ．18B ．16C ．14D ．12【答案】C 【分析】本题考查等边三角形的判定和性质，两点之间线段最短，解题的关键是学会添加常用辅助线，学会利用两点之间线段最短解决最值问题．如图，作点A 关于CM 的对称点A '，点B 关于DM 的对称点B '，证明'' A MB 为等边三角形，即可解决问题．解：如图，作点A 关于CM 的对称点A '，点B 关于DM 的对称点B '，∵120CMD ∠=︒，∴60∠+∠=︒AMC DMB ，∴60''∠+∠=︒CMA DMB ，∴60''∠=︒A MB ，∵MA MB MA MB ''===，∴'' A MB 为等边三角形∵14CD CA A B B D CA AM BD ''''<++=++=，∴CD 的最大值为14，故选：C ．【例2】（22-23八年级上·湖北武汉·期末）如图，锐角ABC V 中，302A BC ∠=︒=，，ABC V 的面积是6，D 、E 、F 分别是三边上的动点，则DEF 周长的最小值是（）A ．3B ．4C ．6D ．7∴AM AE AN ==，MF =∵BAC BAD DAC ∠=∠+∠∴MAN MAB BAD ∠=∠+∠∴(2MAN BAE EAC ∠=∠+∠。

13.4 课题学习最短路径问题第一课时一、内容和内容解析1.内容最短路径问题——将军饮马问题2.内容解析本节课主要以“轴对称知识”、“两点之间，线段最短”、“三角形三边关系”等为基础，来解决数学史上的一个经典问题——“将军饮马问题”，让学生经历将实际问题抽象为数学中的线段和最小问题，接着利用轴对称将线段和最小问题转化为“两点之间，线段最短”的问题，然后再利用“三角形三边关系”对作图进行证明。

最后让学生对所学知识加以应用。

重点：利用轴对称将最短路径问题转化为“两点之间、线段最短”问题，培养学生解决实际问题的能力。

二、目标和目标解析1.教学目标（1）能将实际问题中的“地点”、“一排商铺”抽象为数学中的“点”、“线”，把实际问题抽象为数学问题；（2）能利用轴对称将线段和最小问题转化为“两点之间，线段最短”的问题；（3）能通过逻辑推理证明所求距离最短；（4）体会图形的变换在解决最值问题中的作用，感悟转化思想，进一步获得数学活动的经验，增强应用意识。

2.目标解析（1）将实际问题抽象成数学问题是学生的应具备的能力。

数学来源生活，服务生活。

（2）学生学会将用轴对称最短路径变为“两点之间线段最短”问题三、教学问题诊断分析学生在之前已经学习了“两点之间，线段最短”、“三角形三边关系”、“轴对称”等知识，知道如何去找某点关于某条直线的对称点，为本节课的学习打下了基础。

但是如何将将军饮马问题中的同侧两点问题转化为异侧两点问题，最终用“两点之间线段最短”解决，这是学生不易理解的地方。

本节课教学难点：如何利用轴对称将最短路径问题转化为“两点之间、线段最短”问题；在实际问题中运用最短路径模型灵活解决问题。

关键：运用好数形结合的思想，特别是从轴对称和线段的性质入手，利用轴对称转移线段，从而获得求线段之和最短问题的直观形象，以便准确理解本节课的内容。

四、教学过程设计1.故事引入，引出课题问题1 同学们你们取过包裹快递吗？你们知道双十一吗？播放《直击双11物流现场》视频，激发学生学习兴趣。

轴对称之将军饮马模型重难点题型归纳（五大类型）【题型01 ：“2定点1动点”作图问题】【题型02 ：“2定点1动点”求周长最小值问题】【题型03 ：“2定点1动点”求线段最小值问题】【题型04 ：“1定点2动点”-线段/周长最小问题】【题型05 ：“1定点2动点”-角度问题】【题型01 ：“2定点1动点”作图问题】【典例1】如图，A，B两个村庄独自从河流l上安装了两条灌溉管道AD，BE，AD⊥l于点D，BE⊥l于点E．某水务局准备为两村庄在河流l上重新安装一台大型的抽水设备灌溉农田．通过测量，确定在河流l的点P处安装抽水设备，则到两个村庄铺设的管道AP+BP的长度最短，此时测得∠PBE=30°，DE=150m，则AP+BP的最小值为（ ）A．180m B．210m C．240m D．300m【变式1-1】已知点A，点B都在直线/的上方，试用尺规作图在直线l上求作一点P，使得PA+PB的值最小，则下列作法正确的是()A．B．C．D．【变式1-2】如图，在正方形网格中，点A，B，C在小正方形的顶点上．(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′；(2)连接CC′，直线l与线段CC′的关系是 ；(3)在直线l上确定一点P，使得PB+PC最短（不写作法，保留作图痕迹）．【变式1-3】如图，在小河河岸的同侧，一牧民在A点处放马，现在要到河边去给马饮水，然后再回到点B处．问在何处饮水才能使牧民所走的路程最短？【题型02 ：“2定点1动点”求周长最小值问题】【典例2】如图，△ABC中，AB=AC，BC=6，△ABC的面积为21，AD⊥BC于D，EF是AB边的中垂线，点P是EF上一动点，△PBD周长的最小是等于（）A．7B．8C．9D．10【变式2-1】如图，已知△ABC中，AB=4，AC=5，边BC的垂直平分线分别交BC，AC于点E，F，点D为直线EF上一点，则△ABD的周长最小值为（）A．12B．11C．10D．9【变式2-2】如图，在△ABC中，AB=AC，BC=4，面积是12，AC的垂直平分线EF分别交AB，AC 边于点E，F．若点D为BC边的中点，点P为线段EF上一动点，则△PCD周长的最小值为（ ）A．8B．3C．6D．4【变式2-3】如图，等腰三角形ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为（ ）A．4cm B．5cm C．6cm D．8cm【题型03 ：“2定点1动点”求线段最小值问题】【典例3】如图，在△ABC中，AB=AC，分别以点A、B为圆心，以适当长为半径画弧，两弧分别交于E、F，画直线EF，D为BC的中点，M为直线EF上任意一点，若BC=5，△ABC的面积为15，则BM+MD 的最小长度为（）A．5B．6C．7D．8【变式3-1】如图，在△ABC中，AB=AC,AD=12，D是BC的中点，EF垂直平分AB，交AB于点E，交AC于点F，在EF上确定一点P，使PB+PD最小，则这个最小值为（ ）A．10B．11C．12D．13【变式3-2】如图，△ABC是等边三角形，AD是BC边上的高，且AD=6，E是AC的中点，P是AD上的一个动点，则PC与PE的和最小是（）A．3B．4C．6D．8【题型04 ：“1定点2动点”-线段/周长最小问题】【典例4】如图，BD平分∠ABC，S△ABC＝8，AB＝4，E为BC上一动点，在BD上找一点F，使EF+FC的值最小，则这个最小值为( )A．4B．3C．5D．6【变式4-1】如图，在△ABC中，AB=AC，边AC的垂直平分线MN分别交AB、AC于点M、N，点D是边BC的点，点P是MN上任意一点，连接PD、PC，若∠A=40°，则当△PCD周长最小时，∠CPD=（ ）A ．25°B ．30°C ．35°D ．40°【变式4-2】如图，点E 在等边△ABC 的边BC 上，BE =4，射线CD ⊥BC ，垂足为点C ，点P 是射线CD 上一动点，点F 是线段AB 上一动点，当EP +FP 的值最小时，BF =5，则AB 的长为（ ）A ．6B ．7C ．2D ．10【变式4-3】如图，在等腰三角形ABC 中，AB =AC ，AD ⊥BC ，点D 为垂足，E 、F 分别是AD 、AB 上的动点．若AB =6，△ABC 的面积为12，则BE +EF 的最小值是（ ）A ．2B ．4C ．6D ．8【变式4-4】如图，在△ABC 中，AB =AC =5，S ΔABC =12，AD 是△ABC 的中线，F 是AD 上的动点，E 是AC 边上的动点，则CF +EF 的最小值为（ ）A ．3B ．65C ．125D ．245【变式4-5】△ABC中，∠ACB=90°，∠ABC=30°，AB=8，BD是△ABC的角平分线，点E、F分别是线段BD、线段AB上的动点，则AE+EF的最小值是()A．4B．3C．8D．16【典例5】在某草原上，有两条交叉且笔直的公路OA、OB，如图，∠AOB=30°，在两条公路之间的点P 处有一个草场，OP=4．现在在两条公路上各有一户牧民在移动放牧，分别记为M、N，存在M、N使得△PMN的周长最小．则△PMN周长的最小值是（）．A．4B．6C．8D．12【变式5-1】如图，∠AOB＝30º，∠AOB 内有一定点P，且OP＝12，在OA 上有一动点Q，OB 上有一动点R．若△PQR 周长最小，则最小周长是()A．6B．12C．16D．20【变式5-2】如图，已知∠AOB=α，C是∠AOB内部的一点，且OC=3，点D、E分别是OA、OB上的动点，若△CDE周长的最小值等于3，则α=（）A．45°B．40°C．35°D．30°【题型05 ：“1定点2动点”-角度问题】【典例6】如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC，CD上分别找一点M，N，使△AMN周长最小，则∠AMN+∠ANM的度数为（）A．60°B．120°C．90°D．45°【变式6-1】如图，在五边形ABCDE中，∠BAE=120°，∠B=∠E=90°，AB=BC，AE=DE，在BC、DE上分别找到一点M、N，使得△AMN的周长最小，则∠AMN+∠ANM的度数为（ ）A．100°B．110°C．120°D．130°【变式6-2】如图，在四边形ABCD中，∠A＝∠C＝90°，∠B＝32°，在边AB，BC上分别找一点E，F使△DEF的周长最小，此时∠EDF＝（ ）A．110°B．112°C．114°D．116°【变式6-3】如图所示，在四边ABCD中，∠BAD=120°，∠B=∠D=90°，若在BC和CD上分别找一点M，使得△AMN的周长最小，则此时∠AMN+∠ANM的度数为（）A．110°B．120°C．140°D．150°。

轴对称之将军饮马模型基本图模1.已知：如图定点A、B分布在定直线l两侧；要求：在直线l上找一点P 使PA+PB的值最小解：连接AB交直线l于点P 点P即为所求,PA+PB的最小值即为线段AB的长度理由：在l上任取异于点P的一点P´连接AP´、BP´在△ABP’中 AP´+BP´>AB 即AP´+BP´>AP+BP∴P为直线AB与直线l的交点时 PA+PB最小.2.已知：如图定点A和定点B在定直线l的同侧要求：在直线l上找一点P 使得PA+PB值最小（或△ABP的周长最小）解：作点A关于直线l的对称点A´连接A´B交l于P点P即为所求；理由：根据轴对称的性质知直线l为线段AA´的中垂线由中垂线的性质得：PA=PA´要使PA+PB最小则需PA´+PB值最小从而转化为模型1.方法总结：1.两点之间线段最短；2.三角形两边之和大于第三边两边之差小于第三边；3.中垂线上的点到线段两端点的距离相等；4.垂线段最短.【典例1】（2022春•漳州期末）如图要在街道l设立一个牛奶站O向居民区A B提供牛奶下列设计图形中使OA+OB值最小的是（）A．B．C．D．【答案】D【解答】解：作点A关于直线l的对称点A′连接A′B交直线l于点O则点O即为所求点．故选：D．【变式1】（2021春•成都期末）如图点A B在直线l的同侧在直线l上找一点P使P A+PB最小则下列图形正确的是（）A．B．C．D．【答案】B【解答】解：∵点A B在直线l的同侧∴作A点关于l的对称点A' 连接A'B与l的交点为P由对称性可知AP＝A'P∴P A+PB＝P A′+PB＝A′B为最小故选：B．【典例2】（2022春•埇桥区校级期末）如图Rt△ABC中∠ACB＝90°AC＝6 BC＝8 AB＝10 BD平分∠ABC如果点M N分别为BD BC上的动点那么CM+MN的最小值是（）A．4B．4.8C．5D．6【答案】B【解答】解：如图所示：过点C作CE⊥AB于点E交BD于点M过点M作MN⊥BC于点N∵BD平分∠ABC∴ME＝MN∴CM+MN＝CM+ME＝CE．∵Rt△ABC中∠ACB＝90°AC＝6 BC＝8 AB＝10 CE⊥AB∴S△ABC＝•AB•CE＝•AC•BC∴10CE＝6×8∴CE＝4.8．即CM+MN的最小值是4.8故选：B．【变式2-1】（2022春•河源期末）已知等腰△ABC中AB＝AC E是高AD上任一点F 是腰AB上任一点腰AC＝5 BD＝3 AD＝4 那么线段BE+EF的最小值是（）A．5B．3C．D．【答案】C【解答】解：如图作点F关于AD的对称点F′连接EF′．作BH⊥AC于H．∵AB＝AC AD⊥BC∴BD＝CD＝3∴点F′在AC上∵BE+EF＝BE+EF′根据垂线段最短可知当B E F′共线且与H重合时BE+EF的值最小最小值就是线段BH的长．在Rt△ACD中AC＝5∵•BC•AD＝•AC•BH∴BH＝∴BE+EF的最小值为故选：C【变式2-2】（2021秋•甘南县期末）如图在△ABC中直线l垂直平分AB分别交CB、AB于点D E点F为直线l上任意一点AC＝3 CB＝4．则△ACF周长的最小值是（）A．4B．6C．7D．10【答案】C【解答】解：∵直线l垂直平分AB∴A B关于直线l为对称∴F与D点重合时AF+CF最小最小值是BC＝4∴△ACF周长的最小值＝AF+CF+AC＝AC+CD+BD＝AC+BC＝3+4＝7故选：C．（2022春•南岸区校级期中）如图在Rt△ABC中∠C＝90°∠A＝30°AB 【变式2-3】＝7 BD是△ABC的角平分线点P点N分别是BD AC边上的动点点M在BC上且BM＝1 则PM+PN的最小值为（）A．3B．C．3.5D．【答案】A【解答】解：如图所示作点M关于BD的对称点M' 连接PM' 则PM'＝PM BM＝BM'＝1∴PN+PM＝PN+PM'当N P M'在同一直线上且M'N⊥AC时PN+PM'的最小值等于垂线段M'N的长此时∵Rt△AM'N中∠A＝30°∴M'N＝AM'＝×（7﹣1）＝3∴PM+PN的最小值为 3故选：A．【典例3】（2021春•西乡县期末）如图等腰三角形ABC的底边BC为4 面积为24 腰AC的垂直平分线EF分别交边AC AB于点E F若D为BC边的中点M为线段EF 上一动点则△CDM的周长的最小值为（）A．8B．10C．12D．14【答案】D【解答】解：连接AD MA．∵△ABC是等腰三角形点D是BC边的中点∴AD⊥BC∴S△ABC＝BC•AD＝×4×AD＝24 解得AD＝12∵EF是线段AC的垂直平分线∴点A关于直线EF的对称点为点C MA＝MC∴MC+DM＝MA+DM≥AD∴AD的长为CM+MD的最小值∴△CDM的周长最短＝（CM+MD）+CD＝AD+BC＝12+×4＝14．故选：D【变式3-1】（2021秋•海珠区期中）如图在△ABC中AB＝AC BC＝4 △ABC的面积是14 AC的垂直平分线EF分别交AC AB于E F点．若点D为BC边的中点点M 为线段EF上一动点则CM+DM的最小值为（）A．21B．7C．4D．2【答案】B【解答】解：连接AD∵△ABC是等腰三角形点D是BC边的中点．∴AD⊥BC∴S△ABC＝BC•AD＝×4×AD＝14 解得AD＝7∵EF是线段AB的垂直平分线∴点C关于直线EF的对称点为点A连接AM则CM+DM＝AM+DM≥AD∴当点M在线段AD上时CM+DM的值最小∴AD的长为CM+MD的最小值．故选：B．【变式3-2】如图等腰三角形ABC的底边BC的长为4 面积是16 腰AC的垂直平分线EF分别交AC AB边于E F点若点D为BC边的中点点M为线段EF上一动点则△CDM周长的最小值为（）A．7B．8C．9D．10【答案】D【解答】解：∵EF是AC的垂直平分线∴点A与点C关于EF对称．连接AD与EF的交点为M则此时点M为使△CDM周长最小时的位置．∵点D是底边BC上的中点且△ABC是等腰三角形∴AD⊥BC．∵S△ABC＝16 BC＝4∴AD＝＝＝8．∵MA＝MC∴△CDM的周长＝MC+MD+CD＝AD+DC＝8+2＝10．故选：D【典例4】（2020秋•郧西县月考）如图已知∠AOB的大小为30°P是∠AOB内部的一个定点且OP＝1 点E、F分别是OA、OB上的动点则△PEF周长的最小值等于（）A．B．C．2D．1【答案】D【解答】解：作P点关于OA的对称点P' 作P点关于OB的对称点P'' 连接P'P''交OA 于点E、交BO于点F连接OP'、OP''由对称性可知PE＝P'E PF＝P''F∴△PEF周长＝PE+PF+EF＝P'E+P''F+EF＝P'P''此时△PEF周长最小∵PO＝OP' OP＝OP''∴OP'＝OP''∵∠AOB＝30°∴∠P'OP''＝60°∴△OP'P''是等边三角形∵OP＝1∴P'P''＝1故选：D．【变式4-1】（2021秋•澄城县期末）如图∠AOB＝30°∠AOB内有一定点P且OP ＝15 若在OA、OB上分别有动点M、N则△PMN周长的最小值是（）A．5B．15C．20D．30【答案】B【解答】解：作P关于OA的对称点D作P关于OB的对称点E连接DE交OA于M 交OB于N连接PM PN则此时△PMN的周长最小连接OD OE∵P、D关于OA对称∴OD＝OP PM＝DM同理OE＝OP PN＝EN∴OD＝OE＝OP＝15∵P、D关于OA对称∴OA⊥PD∵OD＝OP∴∠DOA＝∠POA同理∠POB＝∠EOB∴∠DOE＝2∠AOB＝2×30°＝60°∵OD＝OE＝15∴△DOE是等边三角形∴DE＝15即△PMN的周长是PM+MN+PN＝DM+MN+EN＝DE＝15故选：B．【变式4-2】（2021秋•应城市期末）如图∠MON＝50°P为∠MON内一点OM上有点A ON上有点B当△P AB的周长取最小值时∠APB的度数为（）A．60°B．70°C．80°D．100°【答案】C【解答】解：如图分别作P关于OM、ON的对称点P1、P2然后连接两个对称点即可得到A、B两点.∴△P AB即为所求的三角形根据对称性知道：∠APO＝∠AP1O∠BPO＝∠BP2O还根据对称性知道：∠P1OP2＝2∠MON OP1＝OP2而∠MON＝50°∴∠P1OP2＝100°∴∠AP1O＝∠BP2O＝40°∴∠APB＝2×40°＝80°．故选：C．【典例5】（2021秋•丛台区校级期末）如图四边形ABCD中∠BAD＝130°∠B＝∠D＝90°在BC CD上分别找一点M N使△AMN的周长最小时则∠ANM+∠AMN的度数为（）A．80°B．90°C．100°D．130°【答案】C【解答】解：作A点关于CD的对称点F作A点关于BC的对称点E连接EF交CD 于N交BC于M连接AM、AN∵∠B＝∠D＝90°∴AN＝NF AM＝EM∴△AMN的周长＝AM+AN+MN＝NF+MN+EM＝EF此时△AMN的周长有最小值∵∠F AN＝∠F∠E＝∠EAM∴∠E+∠F＝180°﹣∠BAD∵∠BAD＝130°∴∠E+∠F＝50°∴∠BAM+∠F AN＝50°∴∠MAN＝130°﹣50°＝80°∴∠ANM+∠AMN＝180°﹣∠MAN＝100°故选：C．【变式5-1】（2021秋•仁怀市期末）如图在四边形ABCD中∠B＝∠D＝90°∠BAD ＝140°点E F分别为BC和CD上的动点连接AE AF．当△AEF的周长最小时∠EAF的度数为（）A．60°B．90°C．100°D．120°【答案】C【解答】解：作A关于BC和CD的对称点A′A″连接A′A″交BC于E交CD于F则A′A″即为△AEF的周长最小值．∵DAB＝140°∴∠AA′E+∠A″＝180°﹣140°＝40°∵∠EA′A＝∠EAA′∠F AD＝∠A″∴∠EAA′+∠A″AF＝40°∴∠EAF＝140°﹣40°＝100°．故选：C．【变式5-2】（2022春•驻马店期末）如图四边形ABCD中∠BAD＝a∠B＝∠D＝90°在BC、CD上分别找一点M、N当△AMN周长最小时则∠MAN的度数为（）A．a B．2a﹣180°C．180°﹣a D．a﹣90°【答案】B【解答】解：延长AB到A′使得BA′＝AB延长AD到A″使得DA″＝AD连接A′A″与BC、CD分别交于点M、N．∵∠ABC＝∠ADC＝90°∴A、A′关于BC对称A、A″关于CD对称此时△AMN的周长最小∵BA＝BA′MB⊥AB∴MA＝MA′同理：NA＝NA″∴∠A′＝∠MAB∠A″＝∠NAD∵∠AMN＝∠A′+∠MAB＝2∠A′∠ANM＝∠A″+∠NAD＝2∠A″∴∠AMN+∠ANM＝2（∠A′+∠A″）∵∠BAD＝a∴∠A′+∠A″＝180°﹣a∴∠AMN+∠ANM＝2×（180°﹣a）＝360°﹣2a．∴∠MAN＝180°﹣（360°﹣2a）＝2a﹣180°故选：B．【典例6】如图在平面直角坐标系中点C的坐标为（﹣1 5）．（1）若把△ABC向右平移5个单位再向下平移3个单位得到△A1B1C1并写出B1的坐标；（2）求出△ABC的面积；（3）在y轴上找一点P使得P A+PB的值最小（保留作图痕迹不写作法）．【解答】解：（1）如图△A1B1C1即为所求∴B1的坐标（3 ﹣2）；（2）S△ABC＝3×4﹣×2×2﹣×1×4﹣×2×3＝12﹣2﹣2﹣3＝5；（3）作点B关于y轴的对称点B' 连接AB'交y轴于P则点P即为所求．【变式6】如图在平面直角坐标系中点C的坐标为（﹣1 5）．（1）若把△ABC向右平移5个单位再向下平移3个单位得到△A1B1C1并写出B1的坐标；（2）在x轴上找一点P使得P A+PB的值最小.【解答】解：（1）△A1B1C1如图所示．从图象看B1点的坐标是（﹣3 2）．（2）A点关于x轴的对称点A′坐标为（4 ﹣4）连接A'B交x轴于P点则P A+PB＝P A'+PB＝A'B此时P A+PB的值最小1．如图直线L是一条输水主管道现有A、B两户新住户要接水入户图中实线表示铺设的管道则铺设的管道最短的是（）A．B．C．D．【答案】C【解答】解：作点B关于直线l的对称点B' 连接AB′交直线l于M．根据两点之间线段最短可知选项C修建的管道则所需管道最短．故选：C．2．（2022•海港区校级开学）如图在△ABC中AB＝AC＝10 BC＝12 AD＝8 AD是∠BAC的平分线．若P Q分别是AD和AC上的动点则PC+PQ的最小值是（）A．9.6B．8C．6D．4.8【答案】A【解答】解：∵AB＝AC AD是∠BAC的平分线∴AD垂直平分BC∴BP＝CP．过点B作BQ⊥AC于点Q BQ交AD于点P则此时PC+PQ取最小值最小值为BQ 的长如图所示．∵S△ABC＝BC•AD＝AC•BQ∴BQ＝＝9.6．故选：A．3．（2022春•定海区期末）如图直线l1l2表示一条河的两岸且l1∥l2．现要在这条河上建一座桥（桥与河的两岸相互垂直）使得从村庄P经桥过河到村庄Q的路程最短应该选择路线（）A．路线：PF→FQ B．路线：PE→EQC．路线：PE→EF→FQ D．路线：PE→EF→FQ【答案】C【解答】解：作PP'垂直于河岸l2使PP′等于河宽连接QP′与另一条河岸相交于F作FE⊥直线l1于点E则EF∥PP′且EF＝PP′于是四边形FEPP′为平行四边形故P′F＝PE根据“两点之间线段最短”QP′最短即PE+FQ最短．故C选项符合题意故选：C．4．（2022春•沙坪坝区校级期末）如图在△ABC中AD是△ABC的角平分线点E、F 分别是AD、AB上的动点若∠BAC＝50°当BE+EF的值最小时∠AEB的度数为（）A．105°B．115°C．120°D．130°【答案】B【解答】解：过点B作BB′⊥AD于点G交AC于点B′过点B′作B′F′⊥AB于点F′与AD交于点E′连接BE′如图此时BE+EF最小．∵AD是△ABC的角平分线∴∠BAD＝∠B′AD＝25°∴∠AE′F′＝65°∵BB′⊥AD∴∠AGB＝∠AGB′＝90°∵AG＝AG∴△ABG≌△AB′G（ASA）∴BG＝B′G∠ABG＝∠AB′G∴AD垂直平分BB′∴BE＝BE′∴∠E′B′G＝∠E′BG∵∠BAC＝50°∴∠AB′F′＝40°∴∠ABE＝40°∴∠BE′F′＝50°∴∠AE′B＝115°．故选：B．5．（2021秋•天津期末）如图在△ABC中AB的垂直平分线DE交BC于点D垂足为E M为DE上任意一点BA＝3 AC＝4 BC＝6 则△AMC周长的最小值为（）A．7B．6C．9D．10【答案】D【解答】解：如图所示连接BM∵DE是AB的垂直平分线∴AM＝BM∴AM+CM＝BM+CM当B M C在同一直线上时AM+CM的最小值为BC的长又∵AC＝4 BC＝6∴△AMC周长的最小值＝6+4＝10故选：D．6．（2021秋•海丰县期末）如图OE为∠AOB的角平分线∠AOB＝30°OB＝6 点P C分别为射线OE OB上的动点则PC+PB的最小值是（）A．3B．4C．5D．6【答案】A【解答】解：过点B作BD⊥OA交于D点交OE于点P过点P作PC⊥OB交于C点∵OE为∠AOB的角平分线∴DP＝CP∴PB+PC＝PD+PB＝BD此时PC+PB的值最小∵∠AOB＝30°OB＝6∴BD＝3故选：A．7．（2022春•茌平区期末）如图在平面直角坐标系中O为原点点A C E的坐标分别为（0 4）（8 0）（8 2）点P Q是OC边上的两个动点且PQ＝2 要使四边形APQE的周长最小则点P的坐标为（）A．（2 0）B．（3 0）C．（4 0）D．（5 0）【答案】C【解答】解：如图将点E（8 2）往左平移2个单位得到F（6 2）则EF＝2＝PQ EF∥PQ∴四边形EFPQ是平行四边形∴FP＝QE作点F关于x轴的对称点F' 连接PF'则PF'＝PF F'（6 ﹣2）∴当点A、P、F在同一直线上上时AP+PF'最小即AP+EQ最小∵A（0 4）F'（6 ﹣2）∴直线AF'解析式：y＝﹣x+4∴P（4 0）故选：C．8．（2021秋•北安市校级期末）如图等边三角形ABC的边长为6 A、B、A1三点在一条直线上且△ABC≌△A1BC1.若D为线段BC1上一动点则AD+CD的最小值是（）A．10B．12C．16D．18【答案】B【解答】解：连接CA1交BC1于点E∵直线l⊥AB且△ABC与△A1BC1关于直线l对称∴A B A1共线∵∠ABC＝∠A1BC1＝60°∴∠CBC1＝60°∴∠C1BA1＝∠C1BC∵BA1＝BC∴BD⊥CA1CD＝DA1∴C A1关于直线BC1对称∴当点D与B重合时AD+CD的值最小最小值为线段AA1的长＝12故选：B．9．如图AD是等边△ABC的BC边上的中线F是AD边上的动点E是AC边上动点当EF+CF取得最小值时则∠ECF的度数为（）A．15°B．22.5°C．30°D．45°【答案】C【解答】解：如图：过点B作BE⊥AC于点E交AD于点F连接CF∵△ABC是等边三角形∴AE＝ECAF＝FC∴∠F AC＝∠FCA∵AD是等边△ABC的BC边上的中线∴∠BAD＝∠CAD＝30°∴∠ECF＝30°．故选：C．10．如图在△ABC中AB＝AC BC＝4 面积是14 AC的垂直平分线EF分别交AC AB 边于E F点．若点D为BC边的中点点M为线段EF上一动点则△CDM周长的最小值为（）A．10B．9C．8D．6【答案】B【解答】解：连接AD AM∵△ABC是等腰三角形点D是BC边的中点∴AD⊥BC∴S△ABC＝BC•AD＝×4×AD＝14 解得AD＝7∵EF是线段AC的垂直平分线∴AM＝CM当点M在AD上时DM+CM最小最小值为AD∴△CDM的周长最短＝（CM+MD）+CD＝AD+BC＝7+×4＝7+2＝9．故选：B．11．如图已知∠MON＝40°P为∠MON内一定点OM上有一点A ON上有一点B当△P AB的周长取最小值时∠APB的度数是°．【答案】100【解答】解：分别作点P关于OM、ON的对称点P′、P″连接OP′、OP″、P′P″P′P″交OM、ON于点A、B连接P A、PB此时△P AB周长的最小值等于P′P″．由轴对称性质可得OP′＝OP″＝OP∠P′OA＝∠POA∠P″OB＝∠POB∴∠P′OP″＝2∠MON＝2×40°＝80°∴∠OP′P″＝∠OP″P′＝（180°﹣80°）÷2＝50°又∵∠BPO＝∠OP″B＝50°∠APO＝∠AP′O＝50°∴∠APB＝∠APO+∠BPO＝100°．故答案为：100．12．如图AB⊥BC AD⊥DC∠BAD＝116°在BC、CD上分别找一点M、N当△AMN周长最小时∠AMN+∠ANM的度数是．【答案】128°【解答】解：作A点关于BC的对称点E作A点关于CD的对称点F连接EF交BC 于M点交CD于N点∴AM＝EM AN＝NF∴AM+AN+MN＝EM+MN+NF＝EF此时△AMN周长最小由对称性可知∠E＝∠EAM∠F＝∠NAF∵∠BAD＝116°∴∠E+∠F＝180°﹣116°＝64°∴∠MAN＝116°﹣64°＝52°∴∠AMN+∠ANM＝180°﹣52°＝128°故答案为：128°．13．如图在平面直角坐标系中点A（4 4）B（2 ﹣4）．（1）若点A关于x轴、y轴的对称点分别是点C、D请分别描出并写出点C、D的坐标；（2）在y轴上求作一点P使P A+PB最小（不写作法保留作图痕迹）【解答】解：（1）如图所示；C点坐标为；（4 ﹣4）D点坐标为：（﹣4 4）；（2）连接BD交y轴于点P P点即为所求；。

轴对称之将军饮马模型重难点题型归纳（五大类型）【题型01 ：“2定点1动点”作图问题】【题型02 ：“2定点1动点”求周长最小值问题】【题型03 ：“2定点1动点”求线段最小值问题】【题型04 ：“1定点2动点”-线段/周长最小问题】【题型05 ：“1定点2动点”-角度问题】【题型01 ：“2定点1动点”作图问题】【典例1】如图，一条笔直的河l，牧马人从P地出发，到河边M处饮马，然后到Q地，现有如下四种方案，可使牧马人所走路径最短的是（ ）A．B．C．D．【变式1-1】如图，河道l的同侧有M，N两个村庄，计划铺设管道将河水引至M，N两村，下面四个方案中，管道总长度最短的是（ ）A．B．C．D．【变式1-2】已知：如图，点A和点B在直线l同一侧．求作：直线l上一点P，使PA+PB 的值最小．【题型02：“2定点1动点”求周长最小值问题】【典例2】如图，在△ABC中，AB＝AC，BC＝6，面积是30，AC的垂直平分线EF分别交AC、AB边于E、F点，若点D为BC边的中点，点M为线段EF上一动点，则△CDM 周长的最小值为（ ）A．13B．12C．10D．61【变式2-1】如图所示，在边长4为的正三角形ABC中，E、F、G分别为AB、AC、BC的中点，连接BP、GP，则△BPG的周长的最小值是（ ）A．4B．5C．6D．7【变式2-2】如图，在△ABC中，AB＝AC，BC＝4，面积是14，AC的垂直平分线EF分别交AC，AB边于E，F点．若点D为BC边的中点，点M为线段EF上一动点，则△CDM 周长的最小值为（ ）A．10B．9C．8D．6【变式2-3】如图，直线m是△ABC中BC边的垂直平分线，点P是直线m上一动点，若AB＝7，AC＝6，BC＝8，则△APC周长的最小值是（ ）A．13B．14C．15D．13.5【变式2-4】如图，在△ABC中，AC＝BC，AB＝6，△ABC的面积为12，CD⊥AB于点D，直线EF垂直平分BC交AB于点E，交BC于点F，P是线段EF上的一个动点，则△PBD 的周长的最小值是（ ）A．6B．7C．10D．12【题型03 “2定点1动点”求线段最小值问题】【典例3】（2022春•河源期末）已知，等腰△ABC中，AB＝AC，E是高AD上任一点，F 是腰AB上任一点，腰AC＝5，BD＝3，AD＝4，那么线段BE+EF的最小值是（ ）A．5B．3C．D．【变式3-1】（2023春•东港市期中）如图，等腰△ABC的面积为9，底边BC的长为3，腰AC的垂直平分线EF分别交AC、AB边于点E、F，点D为BC边的中点，点M为直线EF上一动点，则DM+CM的最小值为（ ）A．12B．9C．6D．3【变式3-2】（2022春•埇桥区校级期末）如图，Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AB＝10，BD平分∠ABC，如果点M，N分别为BD，BC上的动点，那么CM+MN的最小值是（ ）A．4B．4.8C．5D．6【题型04：“1定点2动点”-线段/周长最小问题】【典例4】（郧西县月考）如图，已知∠AOB的大小为30°，P是∠AOB内部的一个定点，且OP＝1，点E、F分别是OA、OB上的动点，则△PEF周长的最小值等于（ ）A．B．C．2D．1【变式4-1】（2023春•惠安县期末）如图，已知∠AOB＝30°，点P是∠AOB内部的一点，且OP＝4，点M、N分别是射线OA和射线OB上的一动点，则△PMN的周长的最小值是（ ）A．2B．4C．6D．8【变式4-2】（2022秋•应城市期末）如图，∠MON＝50°，P为∠MON内一点，OM上有点A，ON上有点B，当△PAB的周长取最小值时，∠APB的度数为（ ）A．60°B．70°C．80°D．100°【典例5】（2023春•和平区期末）如图，在△ABC中，AD是△ABC的角平分线，点E、F 分别是AD、AB上的动点，若∠BAC＝50°，当BE+EF的值最小时，∠AEB的度数为（ ）A．105°B．115°C．120°D．130°【变式5-1】（2023•明水县模拟）如图，在锐角三角形ABC中，AB＝4，∠BAC＝60°，∠BAC的平分线交BC于点D，M，N分别是AD和AB上的动点，当BM+MN取得最小值时，AN＝（ ）A．2B．4C．6D．8【变式5-2】（2023春•市中区期末）如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AB＝10，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（ ）A．2.4B．4.8C．4D．5【题型05 ：“1定点2动点”-角度问题】【典例6】（2021秋•丛台区校级期末）如图，四边形ABCD中，∠BAD＝130°，∠B＝∠D＝90°，在BC，CD上分别找一点M，N，使△AMN的周长最小时，则∠ANM+∠AMN 的度数为（ ）A．80°B．90°C．100°D．130°【变式6-1】（2022秋•仁怀市期末）如图，在四边形ABCD中，∠B＝∠D＝90°，∠BAD ＝140°，点E，F分别为BC和CD上的动点，连接AE，AF．当△AEF的周长最小时，∠EAF的度数为（ ）A．60°B．90°C．100°D．120°【变式6-2】（2022春•驻马店期末）如图，四边形ABCD中，∠BAD＝a，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，当△AMN周长最小时，则∠MAN的度数为（ ）A．a B．2a﹣180°C．180°﹣a D．a﹣90°。