当前位置：文档之家 › 第十五章 正交曲面坐标系

第十五章 正交曲面坐标系

  • 格式：pdf
  • 大小：318.31 KB
  • 文档页数：23

下载文档原格式

  / 23

合集下载

演示文稿章正交曲线坐标系ppt讲解

演示文稿章正交曲线坐标系ppt讲解

q1
eˆ1
1 H2
q2
eˆ 2
1 H3
q3
eˆ 3
证毕
第13页，共19页。
曲线坐标系下的梯度、散度和旋度
A P(q1, q2 , q3 )eˆ1 Q(q1, q2 , q3)eˆ2 R(q1, q2 , q3)eˆ3
A
1 H1H 2 H 3
(
PH 2 H q1
3
)
(QH 3 H1 ) q2
j
z qi
k
方向余弦： i
1 Hi
x qi
i
1 Hi
y qi
i
1 Hi
z qi
，
基矢量的相 互表示：
i 1 eˆ1 2 eˆ2 3 eˆ3
，
j 1 eˆ1 2 eˆ 2 3 eˆ3
k 1 eˆ1 2 eˆ2 3 eˆ3
第7页，共19页。
弧微分计算公式
(ds)2 (dx)2 (dy)2 (dz)2
y
dy q1 dq1 q2 dq2 q3 dq3 i1 qi dqi qi dqi (i 1, 2, 3)
z
z
z
3 z
z
dz q1 dq1 q2 dq2 q3 dq3 i1 qi dqi qi dqi (i 1, 2, 3)
第8页，共19页。
(ds)2 (dx)2 (dy)2 (dz)2
(q2 q3 ) q3 ( q2 ) q2 ( q3) 0
第14页，共19页。
(PH
2H3
)
(q2
q3
)
( PH 2 H 3 q1
)
q1
( PH 2 H 3 q2
)
q2
( PH 2 H 3 q3来自)q3(q2

几种常见的正交曲线坐标系

几种常见的正交曲线坐标系

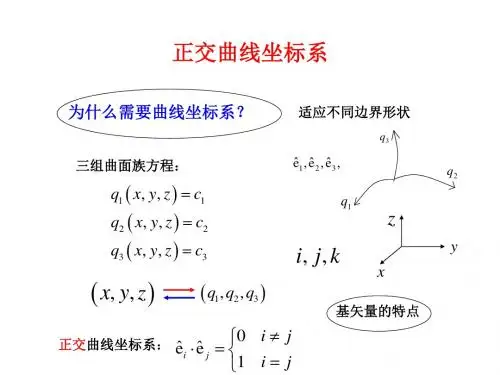
2.3、曲线坐标1）.要研究空间场的性质，首先要对空间加以描述，即在空间建立坐标。

坐标的定义：如果以某种方式使空间的每一个点对应一组有序数()321,,q q q ，而每一组有序数也对应于空间的一个点，这样的有序数称为坐标。

如果有两组坐标()321,,q q q 和()321,,p p p ，这两组坐标由于与空间的点一一对应，所以这两组坐标也一一对应，它们可以互相表示，即()321,,q q q p p i i =；()321,,p p p q q i i =。

=i q 常数，对应于空间的一张曲面，不同的常数对应于不同的曲面。

这就构成了三族曲面，这三族曲面称为坐标曲面。

对于空间的每一个点，每族曲面只有一张曲面过该点。

曲面=2q 常数和=3q 常数的交线称为坐标曲线，在这条曲线上只有1q 可以变化，也称之为坐标曲线1q ，或1q 曲线。

如果空间中每一点的坐标曲线都是正交的（坐标曲线的切线相互正交），则称这样的曲线坐标为正交曲线坐标。

如果每一条坐标曲线都是直线，则称为直角坐标或笛卡尔坐标。

一般用()z y x ,,来表示。

如果用321,,e e e表示321,,q q q 曲线在某一点的切向单位矢量，并指向321,,q q q 增加的方向，习惯上让它们构成右手系。

这样的321,,e e e称为坐标的基矢量。

一般地讲，i e的方向是随空间位置的变化而变化的。

在直角坐标中坐标基矢量的方向是不随空间位置变化的，习惯上用k j i,,表示。

因此在直角坐标中矢径可以表示为：k z j y i x r++=。

作为初步，本课程中只介绍正交曲线坐标。

2）.正交曲线坐标系中对弧的微分 考虑一个微元矢径123112233123i i i ir r r r dr dq dq dq dq ds e ds e ds e ds e q q q q ∂∂∂∂=++==++=∂∂∂∂ 因此，由坐标曲线及基矢量的定义可知i q r ∂ 与i e平行，设ii q rH ∂∂=则()i ie H q r=∂∂i H 称为拉梅系数，一般地讲，拉梅系数i H 是空间的函数。

正交曲线坐标系

正交曲线坐标系

正交曲线坐标系
正交曲线坐标系是一种常用的坐标系，用于描述三维空间中的物
理现象。

在这种坐标系下，坐标轴不再是直线，而是相互交叉的曲线，因此被称为“曲线坐标系”。

正交曲线坐标系通过一组曲线来定义坐标轴，通常是三条互相垂
直的曲线。

这些曲线可以是任意形状的曲线，但是它们必须满足两个
条件：
1.每一组坐标点必须唯一地对应于唯一的位置。

2.在每个坐标点上，这些曲线必须相互垂直。

在三维正交曲线坐标系中，一个点的位置可以用一组数字来表示，这些数字对应于每个轴上与该点相交的曲线的参数值。

例如，在三维
笛卡尔坐标系中，点的位置表示为(x,y,z)，而在三维正交曲线坐标系中，点的位置可能表示为(r,θ,φ)，其中r,θ,和φ是三个互相垂直的曲线的参数值。

正交曲线坐标系可以用于描述许多物理现象，包括电磁场、热力学、量子力学和流体力学等。

例如，在量子力学中，原子轨道可以用
正交曲线坐标系来描述，这些轨道在三维空间中表示为曲线表面。

在
流体力学中，正交曲线坐标系可以用来描述某些复杂的液体流动模式。

正交曲线坐标系也有一些应用限制。

由于曲线定义了坐标轴的形状，因此计算难度较高，而且它们通常只能适用于特定的物理问题。

此外，正交曲线坐标系的变换公式很难推导和应用，因此需要更高的
数学技能和计算机辅助工具才能进行计算和分析。

总之，正交曲线坐标系是一种常用的坐标系，可以用于描述三维
空间中的物理现象，并且在某些情况下可以提供更简单的分析方法，
但由于其特殊性质和较高的计算难度，使用时需要谨慎考虑。

三种常用的正交坐标系程

三种常用的正交坐标系程

张量分析
z
1、直角坐标系 坐标变量
z z0 （平面）
ez
x, y, z
o
坐标单位矢量 ex , e y , ez
位置矢量 线元矢量
ex
P
ey
点 P(x0,y0,z0)
y y y0（平面）
r ex x e y y ez z
dl ex dx ey dy ez dz
o
x
dx d y dSx exdydz
y
体积元
南京工业大学
dV dxdydz
直角坐标系的长度元、面积元、体积元
张量分析 2、圆柱面坐标系
坐标变量
, , z
坐标单位矢量 e , e , ez r e ez z 位置矢量 线元矢量 dl e d e d ez dz
x1 x 2 x 3 g1 1 i 1 j 1 k x x x x1 x 2 x 3 g2 2 i 2 j 2 k x x x x1 x 2 x 3 g3 3 i 3 j 3 k x x x
3
1
x3' g3 g2 O
1 v1 v v 2 r 2 v 2 0 r sin 2 v 3 r sin 2 v 3
面元矢量
dS e dl dl z e ddz dS e dl dl z e ddz dS z ez dl dl ez dd
体积元
南京工业大学
dV dddz
张量分析 3、球面坐标系 坐标变量
坐标单位矢量 er , e , e

CAGD第十五章三角Bézier曲面

CAGD第十五章三角Bézier曲面

第十五章 三角Bézier 曲面在第十章、第十一章和第十二章，我们介绍了双三次Hermite 曲面、Bézier 曲面和B 样条曲面等。

无论其构成方式如何，都是定义在矩形参数域上，并且给定的数据信息具有矩形拓扑结构，曲面片具有四条边界。

然而，在实际工程应用中，并不是所有给定的数据信息都具备矩形拓扑结构，或者说，并非所有的形体表面都仅能通过使用四边曲面片来表示。

那么就需要引入三角曲面片。

三角曲面片和四边曲面片除了拓扑结构不同外，并没有其他本质上的区别。

在四边曲面中，参数v u ,和参数域由矩形区域]1,0[]1,0[ ⨯定义，在三角曲面中，其参数则由重心坐标给出。

三角域上的多项式曲面首先由de Casteljau 于1959年引入。

以另外的形式，比方Lagrange 形式广泛用于有限元分析之中。

其最常用的方法是Clough-Tocher 方法和五次二十一参数插值方法。

二十世纪七十年代，出现了许多三角曲面插值方法，如BBG 插值方法、三角Bézier 曲面片、多元B 样条、Box 样条等。

三角曲面片技术主要用于非规则形体的建模和散乱数据的数值处理，象实验数据处理、地形图生成当中的无噪声插值、有噪声拟合等等。

在三角曲面技术中，应用组为广泛的是三角Bézier 曲面片，它是按照定义在规则三角剖分上的二元Bernstein 基函数来构造曲面的。

本章将主要就这种三角曲面片及其相关技术予以介绍和讨论。

14.1 重心坐标在平面上可以建立各种坐标系，使其几何点与代数有序数组一一对应。

当选用笛卡尔坐标系时，便得到了常用的直角坐标。

如果选择仿射坐标系，则引入点的重心坐标。

给定平面上不共线的三个点321,,T T T ，那么可构成一三角形ℑ，从而平面上任一点P 可表示为：∑==31i i i T P τ （14.1.1）三元组),,(321τττ 称为点P 相应于三角形ℑ的重心坐标，满足条件：1:31==∑=i i ττ （14.1.2）重心坐标的物理意义是质心，它与直角坐标的关系是：∑∑====3131,i y i i y i x i i x T P T P ττ可通过三角形的有向面积计算如下：),,(),,(,),,(),,(,),,(),,(321213321312321321T T T P T T T T T T P T T T T T T P area area area area area area ===τττ （14.1.3）其中：227 第十五章 三角Bézier 曲面11121),,(321321321y y yx x xarea T T T T T T T T T = 按其字母顺序，顺时针旋转为正，逆时针旋转为负。

第二讲：三种常用的正交坐标系、梯度、散度1

第二讲：三种常用的正交坐标系、梯度、散度1
1.2 三种常用的正交坐标系 1.3 标量场的梯度 1.4 矢量场的通量与散度 1、了解三种常用坐标系的特点； 2、熟悉球坐标、柱坐标的基矢，基矢变化及空间微元表示； 3、理解梯度的物理意义，掌握其计算公式。 重点：1、基矢及空间微元表示， 2、梯度的物理意义及计算公式。 难点：基矢的变化。 讲授、练习 学时：2 学时
作业：思考题：1.6;练习题：1.10，1.11，1.12
222rxxyyzz???12y?22???xe???xeyzyzxxeyyezzrrrrreerxyzrxxyzz???????????????2y?3r3222???xe11111???xeyzyzxxeyyezzreerxr???yr???zr???rrxxyzz??????????????????????????3frfrfrfrdrdr??????xe?yzxyzdfrdfrrreeeeerxyzxyz???????????????????同理
u l
M0
，称之为标量场在
M0
处沿 l
的方向导数，它表示标量场
u M 在一个点处沿某一方向对距离的变化率。
方向导数的数值与所取的方向有关。但它不是矢量。
2、方向导数的计算公式
方向导数的定义与坐标系无关，可以选择任意坐标系来计算。在直角坐标系下：
u u x u y u z x y z
所以，
u l
，
eˆ l
eˆx
cos
eˆ y
cos
eˆz
cos
则
u G eˆ G cos G, eˆ
l
l
l
上面的讨论中，G 是一个与方向 eˆl 无关的量。上式表明：沿某一方向的方向导数等
于 G 矢量在该方向上的投影。当 G, eˆ

正交曲线坐标系

正交曲线坐标系

P (x, y, z)
P,, z
三维空间中同一点可以用不同的 正交曲线坐标系描述。不同坐标 系之间存在相互变换关系，这种 变换关系只能是一一对应的
1.1.2 不同坐标系之间的变换
qi qi (x, y, z) C, i 1,2,3
正交曲线坐标系与直角坐标系之间的转换公式
eˆqi
ee M e e e e
x qi
2
＋
y qi
2
z 2
qi
dqi h di q
i
hi
x
2 ＋
y
2系数
i 1,2,3
1.1.3 弧长：一般公式
例：求球坐标系的Lame系数
x r sin cos y r sin sin z r cos
x sin cos
1.1 正交曲线坐标系
自强●弘毅●求是●拓新
1.1 正交曲线坐标系
z P (x, y, z)
y x
三维空间任意点的位置可 通过三条相互正交曲线的 交点来确定。该三条正交 曲线组成确定三维空间任 意点位置的体系称为正交 曲线坐标系，三条正交曲 线称为坐标轴，描述坐标 轴的量称为坐标变量。
1.1.1 单位矢量
z
x2 y2 z2
cos1 x
x2 y2
x r sin cos y r sin sin z r cos
r x sin cos
x r
r y
ry
sin
sin
r z cos
z r
eˆ cos cos 球坐标 系
x
r sin
y
cos
seiˆn
x
y
cos
sin
0

曲面坐标

曲面坐标

图中横坐标ζ和ζf均改成φ，右边的纵坐标θf 改成η
——β以及η的确定，（ψ，η，φ）坐标系的Jacobian J1
由磁场在正交磁面坐标系中的表达式（2.9）及矢量散度的公式（1.18），有
( ) ( ) ( ) ∇
⋅
v B
≡
1∂ g ∂ξ i
g Bi
=∂ ∂θ
J0B2
+∂ ∂φ
J0B3
≡ 0.
(3.1)
=
1 2π
ψ
pol
=
1 2π
Bv
⋅
v dS
=
1 2π
Bv ⋅ (J0∇θdφdψ )
S pol
∫ ∫ =
1 (2π
)
2
Bv
⋅ ∇θ
( J 0dθdφdψ
)
=
1 (2π
)2
Bv ⋅ ∇θd 3r,
(2.2)
是从磁轴到此磁面的极向磁通（单位φ角平均值）；φ是沿大环的环向角；而对 应于极向角，但θ不是小柱坐标系的极向角，通过对它的挑选，使（ψ，θ，φ） 构成一个右手正交系。下面是对这种选择过程的描述。
g ij
=
1 g Gij ,
Gij 是g ij的代数余子式.
(1.12)
——在曲面坐标系中的矢量及其代数、微分运算
任一矢量 A 可以表示成
v A
=
Ai evi
=
Aievi ,
Ai = g ijevj , Ai = gijev j .
代数运算
v A
⋅
v B
=
Ai Bi
=
Ai Bi ,
(
v A
×
v B
)i
[2]. L. S. Solovev and V. D. Shafranov, ‘Plasma confinement in closed magnetic systems’ in “Reviews of Plasma Physics” Vol.5 Edited by M. A. Leontovich, 1967, Consultants Bureau, pp. 15,16, 20.

《正交曲面坐标系》PPT课件

《正交曲面坐标系》PPT课件

1 r
r

r
v r


1 r2
2v
2

2v z 2

k
2v

0
逐次分离变量，令 v(r,, z) w(r,)Z(z) 代入方程
Z
1 r
r

r
w r


Z
1 r2
2w
2

w
d2Z dz2

k 2wZ

0
两边同除以 wZ 得：
1 w
ds2
gijdqidq j
i, j1,2,3


i 1,2,3
x qi
dqi
2


i 1,2,3
y qi
dqi
2


i 1,2,3
z qi
dqi
2
(sin cosdr r cos cosd r sin sind )2
2
是坐标轴的度规因子，
令 ds
gijdqidq j
i, j1,2,3
x 2
y 2
z 2
其中 gij g ji qiq j qiq j qiq j
判定
若 gij=giidij ，则 (q1, q2, q3) 为正交曲面坐标系。 即 ds (h1dq1)2 (h2dq2 )2 (h3dq3 )2 或 hij 0 (i j)
r2
R
得
r2 R
1 d r r dr
dR r 2(k 2 dr
)

1

d 2 d 2

1.6 正交曲线坐标系

1.6 正交曲线坐标系

微分体积元为
dV d l i ( d l j d l k ) hi h j h k du i du j du k
6
2．常用的正交曲线坐标系
常用的正交曲线坐标系除了直角坐标系外，还有柱坐标系和 球坐标系。 z （1）柱坐标系 在此坐标系中P点的位置是由ρ =常数 ρ 的圆柱面、φ =常数的平面和z=常数的平 P(ρ ,φ ,z) 面三者的交点来确定的。这时， z
2
d l e u 1 dl 1 e u 2 dl 2 e u 3 dl 3
或者
dl
d l e u 1 ( h1 du 1 ) e u 2 ( h 2 du 2 ) e u 3 ( h3 du 3 )
dl [( dl 1 ) ( dl 2 ) ( d标系中的梯度、散度和旋度
1．一般正交曲线坐标系中的梯度、散度和旋度
（1）梯度
v v v e u1 eu 2 eu3 l1 l2 l3
dl 1 h 1du 1
1
dl
2
du h2
2
dl
3
h du 3
3
1 1 e u1 e u2 e u3 h1 u 1 h2 u 2 h3 u 3
Ar A A sin cos cos cos sin sin sin cos sin cos cos A x sin A y 0 Az
dV d d dz
这里
h1 1, h 2 , h3 1
柱坐标系与直角坐标系的变换关系：
x cos y sin z z

专题：正交曲线坐标系资料

专题：正交曲线坐标系资料

(q1 i q1 j q1 k) (q2 i q2 j q2 k) (q3 i q3 j q3 k) q1 x y z q2 x y z q3 x y z

q1
q1

q2
q2

q3
q3

dq1

z q2
dq2

z q3
dq3

3 i 1
z qi
dqi

z qi
dqi (i
1, 2,3)
(ds)2 (dx)2 (dy)2 (dz)2
h12 (dq1)2 h22 (dq2 )2 h32 (dq3 )2
r r
r r
r r
2 q1 q2 dq1dq2 2 q1 q3 dq1dq3 2 q2 q3 dq2dq3
h1eˆ1 h2eˆ2 h3eˆ3 A 1
h1h2h3 q1 q2 q3 A1h1 A2h2 A3h3
(qi

1 hi
eˆi )
证明： A Peˆ1 Qeˆ2 Reˆ3
(qi

1 hi
eˆi )
A1h1q1 A2h2q2 A3h3q3

P



Q


R
z

eˆ eˆ eˆ z A 1
z P Q R
Cylindrical coordinates
2u

u

1






u







第九章正交曲面坐标系

第九章正交曲面坐标系
1 d dR 2 µ r + k − λ − 2 R = 0 r dr dr r
d 2Z + λZ = 0
d 2Φ dφ
2
+ µΦ = 0
∇2v + k2v = 0
1 ∂ ∂v 1 ∂2v ∂2v 2 r + 2 2 + 2 + k v = 0 r ∂r ∂r r ∂φ ∂z
u0(r,φ) = R0(r)Φ0(φ) = C0 + D0 lnr
um1(r,φ) = Rm(r)Φm1(φ) = (Cm1r m + Dm1r −m )sinmφ
um2(r,φ) = Rm(r)Φm2(φ) = (Cm2r m + Dm2r −m )cos mφ
一般解：
u(r,φ) = C0 + D0 lnr +
dz
2
d 2Φ dφ
2
+ µΦ = 0
1 d dR 2 µ r + k − λ − 2 R = 0 r dr dr r
柱函数
9.4 亥姆霍兹方程在球坐标系下的分离变量
球坐标系下，亥姆霍兹方程 ∇2v + k2v = 0 的具体形式为：
1 ∂ 2 ∂v 1 1 ∂ ∂v ∂2v + k2v = 0 r + 2 sinθ + 2 2 ∂θ r sin θ ∂φ 2 r 2 ∂r ∂r r sinθ ∂θ
cos2π λ −1 A、B有非零解 ⇔ =0 cos2π λ −1 − sin2π λ sin2π λ
λm = m2, m = 1,2,3⋯
相应的A、B为任意值
本征函数 Φm1(φ) = sinmφ, Φm2(φ) = cosmφ

两种正交曲线坐标系单位矢量间的一般表达式

两种正交曲线坐标系单位矢量间的一般表达式

两种正交曲线坐标系单位矢量间的一般表达式ΞGeneral Expression s Between Un it Vectors of TwoCurv ili near Orthogonal Coord i nate System s易辉跃　唐　斌　晏才宏　周希朗(上海交通大学电子工程系,上海200030)Y I Huiyue ,TANG B i n ,YAN Ca ihong ,ZHOU X ilang(D ep a rt m en t of E lectron ic E ng ineering ,S hang ha i J iaotong U n iversity ,S hang ha i 200030)【摘要】　本文采用不同的分析思路,导出了曲线坐标系与直角坐标系单位矢量间简明的解析关系,并推广到更一般的情况—任何两种正交曲线坐标系单位矢量间的关系。

只要一种正交曲线坐标系与直角坐标系或另一种正交曲线坐标系坐标间的单值关系已知,利用这些关系式即可得到正交曲线坐标系与直角坐标系或另一种正交曲线坐标系单位矢量间的关系。

利用文献上已有的正交曲线坐标系坐标间的单值关系,文中提供了正交曲线坐标系与直角坐标系及圆柱坐标系单位矢量间的变换矩阵,进而可得任何两种正交曲线坐标系单位矢量间的关系。

关键词:　正交曲线坐标系,单位矢量,变换矩阵Abstract :　Concise exp ressi on s betw een un it vecto rs of cu rvilinear o rthogonal coo rdinate system s and tho se of cartesian coo rdinate system w ere derived in term s of differen t analytical ideas.T hese exp ressi on s w ere expanded to mo re general relati on s betw een un it vecto rs of tw o cu rvilinear o rthogonal coo rdinate system s.W ith the help of these exp ressi on s ,relati on s betw een un it vecto rs of a cu rvilinear o rthogonal coo rdinate system and tho se of cartesian coo rdinate system o r ano ther cu rvilinear o rthogonal coo rdinate system can easily be ob tained as long as the single 2value relati on s betw een these tw o coo rdinates are know n .By m ean s of the relati on s betw een cu rvilinear o rthogonal coo rdinates p rovided by o ther au tho rs ,the tran sfo rm ati on m atrixes betw een un it vecto rs of cu rvilinear o rthogonal coo rdinate system s and tho se of cartesian coo rdinate system o r ano ther cu rvilinear o rthogonal coo rdinate system w ere given .Key ter m s :　Cu rvilinear o rthogonal coo rdinate ,U n it vecto r ,T ran sfo rm ati on m atrix一、引 言众所周知,根据求解实际电磁场边值问题的需要,人们已引出了十多种正交曲线坐标系,给出了多种正交曲线坐标系的坐标与直角坐标系、圆柱坐标系等坐标间的关系,并提供了各种坐标系的度量因子(拉梅系数)〔1〕,为在不同坐标系下求解电磁场问题提供了方便。

正交曲线坐标系应变张量的普适表达

正交曲线坐标系应变张量的普适表达

笛 卡儿 坐 标 系 变 换 到 曲线 坐 标 系 的 坐 标 变 换 矩 阵 ［ 的列 向量 彼 此不平 行 ， ］中 同样 由 曲线 坐标 系变 换 到 笛卡 儿 坐标 系 的 坐标 变 换 矩 阵 ［ ］ 的行 中
向量也彼此不平行 ， 但对于正交曲线 坐标 系 ， ［ ］ 中的列 向量彼 此是 正 交 的 ， 一］ ［ 中的行 向量 也 是 彼此正交的， 正向及其逆向雅可 比行列式不等于零 ， 则意 味着地表 上 的某 质 点 不 能 撕 裂 为 二个 质 点 ， 两 个质 点也 不可 能重 叠 加 为 一 个 质 点 ， 正 是 我们 采 这 用弹 性连 续体 进行 应变 分析 的理论 基 础 ｌ 。 ４ ］ 例如对 于球 坐标 系 ， 其雅 可 比行列式 Ｊ＝ｄｔ ｅ ［ ＝１ｓ Ｏ ， Ｔ］ ｉ 只有 在 区域 为 ｒ ， ≠０ １的 联 ２ｎ ＞０ ０ ，Ｔ
文章 编 号 ：６ １５ ４ （ ０ ８ ０ － ８ －８ １７ ．９ ２ ２ ０ ） ４０ ９０ ０
正 交 曲线 坐 标 系 应 变 张 量 的 普 适 表 达
刘 序俨 季 颖 锋 梁全 强
、
／ ） 建省地震局 ， 州 １福 福
３ ０ ０ ５０３
＼ ） 门地 震勘测研究 中心 ， 门 ３ １２ ／ ２厦 厦 ６ ０ １
图
个 参考 面 ， 氏空 间 的任 意一 点 的 曲线 坐 标 就 可 以 欧 这样 定 义 ： 两个 坐 标 为该 点 至 参 考 面 的法 线 投 影 前 在该 面上 的曲线 坐标 ｑ 与 ｑ 为 该 点 的坐 标 ， 作 该 点至 参考 面 的法线距 离 ｑ 作 为 该点 的第三 个 坐标 ， ， ｑ 、 两 条 坐标 曲线在 参 考 面上 形 成 了一 组 相互 正 ｑ

曲面坐标

曲面坐标

=
1 2π
ψ
pol
=
1 2π
Bv
⋅
v dS
=
1 2π
Bv ⋅ (J0∇θdφdψ )
S pol
∫ ∫ =
1 (2π
)
2
Bv
⋅ ∇θ
( J 0dθdφdψ
)
=
1 (2π
)2
Bv ⋅ ∇θd 3r,
(2.2)
是从磁轴到此磁面的极向磁通（单位φ角平均值）；φ是沿大环的环向角；而对 应于极向角，但θ不是小柱坐标系的极向角，通过对它的挑选，使（ψ，θ，φ） 构成一个右手正交系。下面是对这种选择过程的描述。
A(ψ ) +
∂Λ ,
∂θ
(3.5.1)
其中的第一项在取比例中项（中值）后，可以将A(ψ)移出积分，再用ψpol=2πψ， 就得（3.4）；而第二项在积分后，由于在θ上的周期性而为零。
而在磁面 ψ → ψ + dψ 间的极向磁通为
∫ ∫ ∫ dψ
pol
=
1 2π
ψ + dψ
dψ
ψ
2π dθ
0
2π 0
dSt = J0∇φdθdψ ,
有环向磁通
∫ ∫ ψ t (ψ ) =
v B
⋅
dSt
=
1 2π
v B
⋅
∇φd
3r.
S tor
环向总电流
∫ ∫ It (ψ ) =
vj
⋅ dSt
=
1 2π
vj ⋅ ∇φd 3r.
S tor
极向总电流
∫ ∫ I p (ψ ) =
vj
⋅
dS p
=
1 2π

正交曲线坐标系应变张量转换及其在地壳形变分析中的应用的开题报告

正交曲线坐标系应变张量转换及其在地壳形变分析中的应用的开题报告

正交曲线坐标系应变张量转换及其在地壳形变分析中的应用的开题报告1.研究背景和意义地壳运动是地球科学中的热点问题，其研究对于预测地震、地质灾害和地质资源的勘探和利用具有重要的意义。

地球物理学和地球动力学中经常使用应变张量来描述地壳的形变状态，而应变张量在不同的坐标系下的表示方式也是地球物理学家和地球动力学家所关注的问题之一。

Orthogonal Curvilinear Coordinate System (OCCS)是一种与离散点框架无关的坐标系，广泛应用于地球物理学、流体力学和结构力学中的数值模拟计算。

本研究的意义在于通过正交曲线坐标系的应变张量转换方法，将其应用于地壳形变的分析，为地震监测和地质资源勘探提供更精确的地壳形变信息。

2.研究思路和方法本文将研究正交曲线坐标系下的应变张量表示方法和其在地壳形变中的应用。

具体研究内容包括以下两个方面：2.1 正交曲线坐标系应变张量的表示首先，将任意坐标系下的应变张量表示为Cartesian坐标系下的张量形式，然后利用正交曲线坐标系的定义，推导正交曲线坐标系下的应变张量表示方法。

在此基础上，讨论应变张量在正交曲线坐标系下的对称性、对角化及应力量的正交曲线坐标系中的表示。

2.2 正交曲线坐标系在地壳形变分析中的应用将正交曲线坐标系应变张量转换方法应用于地壳形变分析中，大地测量、地震、地质灾害等方面的应用均有可能。

例如，在地震监测中，将地震产生的应变场进行正交曲线坐标系下的转换表示，可以更好地分析地震活动的发展趋势和预测地震发生的概率，为人们提供更为准确的地震信息。

3.研究进展和计划目前，我们已经完成了正交曲线坐标系应变张量的表示方法的理论推导和计算公式的推导，并且进行了一些数值实验验证。

接下来，我们将对正交曲线坐标系在地壳形变分析中的应用进行研究，并进行实际数据的分析和计算。

同时，我们也将对结果进行详细的解释和讨论，并对研究成果进行评估和总结。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
∗ ∗
d (a1 dx1 + a2 dx2 + a3 dx3 ) √ √ 1 ∂ det G 1 ∂ det G = √ a1 + √ a2 1 2 ∂x g ∂x g22 11 det G det G √ 1 det G ∂ √ + a3 . 3 ∂x g33 det G
∗ ∗
正交曲线坐标系中的Laplace算符 分形式．
§15.1 正交曲面坐标系
第2页
§15.1 正交曲面坐标系
作为这些平面极坐标系、柱坐标系、球坐标系等的概括与推广，可以定义曲面坐标系① {x1 , x2 , x3 }， x1 = ξ (x, y, z ), 它的坐标面是三组曲面 x1 = 常数, x2 = 常数, x3 = 常数. x2 = η (x, y, z ), x3 = ζ (x, y, z ),
§15.2 正交曲面坐标系中的Laplace算符
“∗ ”算符是一个线性变换，它把p次微分形式变换为相应的n − p次微分形式 √ det G I gii ∗ i dx = dx , ∗ dxI = √ dxi , gii det G
第5页
其中(i, I )构成(1, 2, 3)的偶排列，det G表示矩阵G的行列式值． 运算法则4
k=1,2,3 k=1,2,3
a11 a12 a22 a32 a13 a23 a33
aki akj = δij .
§15.3 Laplace算符的平移、转动和反射不变性
∗ ∗
1 ∂ r ∂r
r
∂ ∂r
+
1 ∂2 ∂2 + . r2 ∂θ2 ∂z 2
r2 ∂ ∂θ
∂u ∂r sin θ r2
sin θdr ∧ dθ ∧ dφ ∂u ∂θ + dθ ∧ dφ ∧ dr + 1 ∂ sin θ ∂θ 1 ∂2u dφ ∧ dr ∧ dθ, sin θ ∂φ2 ∂u ∂θ + 1 r2 sin2 θ ∂2u . ∂φ2
外微分算符d在不同坐标系中的表达式， ∂f i ∂f dxi = dy . df = i ∂x ∂y i
i i
一次微分形式df 给出的正是梯度grad f ≡ ∇f 的协变微分形式, {dxi , i = 1, 2, 3}构 √ 成一组正交基(正交标准基应该是 gii dxi , i = 1, 2, 3)． 外微分算符d可以作用在p次微分形式α = dα = d
2
2
其中 gij = gji =
① 这里的xi
∂x ∂x ∂y ∂y ∂z ∂z + + . ∂xi ∂xj ∂xi ∂xj ∂xi ∂xj
(i = 1, 2, 3)中，上标i标记空间点的坐标(分量) ，并不表示方次．
② 这种讨论方法的一个优点是可以直接推广到高维空间的情形． ③ 在微分几何中，更常略去式中的和号，而直接写成
§15.2 正交曲面坐标系中的Laplace算符
第4页
§15.2 正交曲面坐标系中的Laplace算符
通过外微分法介绍正交曲线坐标系中Laplace算符的一般形式． 这种方法的优点在于它的协变性，即可以脱离开坐标系的具体定义，而得到最普遍 的表达式． 作为最初步的介绍，略去数学上的严格定义，只给出有关的运算规则． 外微分法则 介绍外微分算符、∗ 算符及楔积运算，以及微分形式的概念． 外微分算符d．它作用在(标量)函数f 上， d : f → df = 得到的df 称为一次微分形式(简称一次形式)． 例 3 对于柱坐标系， du = 例4 对于球坐标系， du = 运算法则1 ∂u ∂u ∂u dr + dθ + dz. ∂r ∂θ ∂z ∂u ∂u ∂u dr + dθ + dφ. ∂r ∂θ ∂φ ∂f dxi , ∂xi
¢¤£¤"¨#$¥¤¦§©%
¡
4
第十五章 正交曲面坐标系
第1页
第十五章 正交曲面坐标系
要能应用分离变量法，取决于两个条件：一个是所讨论的空间区域形状，一个是定 解问题的数学形式． 如果限于第十二章中所涉及的几种典型齐次方程，可以用Helmholtz方程 ∇2 u + k 2 u = 0 统一描述它们的空间部分．这个方程在直角坐标系中是可以分离变量的． 对于所讨论的空间区域，总要适当地放置坐标架，使得区域的边界面与坐标面重 合，从而实现齐次边界条件的分离变量． 如果我们所要讨论的空间区域，是圆柱形(包括它的特殊情形，二维平面上的圆形 区域)或球形，乃至其他更特别的形状，如果仍然选择直角坐标系，无论怎样放置 坐标架，总不能使得区域的边界面全部都和坐标面重合．因此，即使边界条件是齐 次的，也无法分离变量． 解决这个问题的办法是选用合适的坐标系： • 圆形区域，首选平面极坐标系 • 圆柱形区域，首选柱坐标系 • 球形区域，首选球坐标系 在这些坐标系下，Laplace算符的具体形式如何？ Helmholtz方程是否可以分u ∂r
r2
sin θ
所以，Laplace算符在球坐标系下的表达式是 ∇2 ≡ 1 ∂ r2 ∂r r2 ∂ ∂r + 1 ∂ sin θ ∂θ sin θ ∂ ∂θ + 1 r2 sin2 θ ∂2 . ∂φ2
r2
§15.3 Laplace算符的平移、转动和反射不变性
= 0.
对于空间的任意一点，如果通过该点的三个坐标面总是互相垂直的，那么，这个坐标系就 称为正交曲面坐标系．例如，在直角坐标系中，过空间任意一点(x0 , y0 , z0 )的三个坐标面 x = x0 , 就是互相垂直的． 为了判断一个坐标系是不是正交曲面坐标系，当然可以直接由坐标系的定义求出坐标面的 法矢量来判断．更常用的办法② 是计算出弧长③ ds2 = dx2 + dy 2 + dz 2 = + + =
d d是Laplace算符∇2 ≡ ∇ · ∇ ≡ div grad的协变微
§15.2 正交曲面坐标系中的Laplace算符
第6页
例 7 柱坐标系， d∗ du = ∂ ∂r +r r ∂u ∂r dr ∧ dθ ∧ dz + 1 ∂2u dθ ∧ dz ∧ dr r ∂θ2
∂2u dz ∧ dr ∧ dθ, ∂z 2 1 ∂ ∂u 1 ∂2u ∂2u ∗ ∗ d du = r + 2 2 + . r ∂r ∂r r ∂θ ∂z 2 因此，Laplace算符在柱坐标系下的表达式是 ∇2 ≡ 例 8 球坐标系， d∗ du = ∂ ∂r +
i,j =1,2,3
y = y0 ,
z = z0
∂x ∂x ∂x dx1 + dx2 + dx3 ∂x1 ∂x2 ∂x3
2
∂y ∂y ∂y dx1 + dx2 + dx3 1 2 ∂x ∂x ∂x3 ∂z ∂z ∂z dx1 + dx2 + dx3 ∂x1 ∂x2 ∂x3 gij dxi dxj ,
∗
d(a1 dx1 + a2 dx2 + a3 dx3 ) = + + ∂a3 ∂a2 − ∂x2 ∂x3 ∂a1 ∂a3 − ∂x3 ∂x1 ∂a1 ∂a2 − ∂x1 ∂x2 √ g11 dx1 det G √ √ g22 dx2 det G g33 dx3 det G
看出．
∗ ∗
d 是散度div的协变微分形式，
因此，Laplace算符在平移变换下是不变的，即 ∂2 ∂2 ∂2 ∂2 ∂2 ∂2 + + ≡ + + . ∂x2 ∂y 2 ∂z 2 ∂x 2 ∂y 2 ∂z 2 Laplace算符的转动不变性 坐标轴的不同取向，涉及到坐标系之间的正交变换． 设空间一点在变换前后的坐标分别是{x, y, z }和{x , y , z }， x a11 a12 a13 x y = a21 a22 a23 y . z z a31 a32 a33 所谓正交变换，指的是变换矩阵 A= a21 a31 满足正交关系 aik ajk =
第7页
§15.3 Laplace算符的平移、转动和反射不变性
选定坐标系以后，在求解定解问题时，往往还需要考虑两个问题． • 坐标架如何放置，包括坐标原点位置和坐标轴特殊取向的选择，以最大限度地 利用问题中的对称性，使求解过程得到充分的简化 • 定解问题的对称性与解的对称性之间的联系 这两个问题实际上并不可截然分开． 坐标架的不同放置，数学上就表现为不同坐标系之间的线性变换． 在这些线性变换下，Laplace算符的形式如何变化，上一节已经作出了原则的回 答：Laplace算符的形式具有不变性． Laplace算符的平移不变性 坐标原点的不同放置，涉及到的是平移变换， x = x − a, 容易看出， ∂2 ∂2 2 = ∂x2 , ∂x ∂2 ∂2 2 = ∂y 2 , ∂y ∂2 ∂2 2 = ∂z 2 . ∂z y = y − b, z = z − c.
空间任意一点的坐标(x1 , x2 , x3 )，就由过该点的三个坐标面决定．为了保证x1 , x2 和x3 是独立 的，应当要求它们的Jacobi行列式 ∂x1 ∂x ∂ (x1 , x2 , x3 ) ∂x2 ≡ ∂ (x, y, z ) ∂x ∂x3 ∂x ∂x1 ∂y ∂x2 ∂y ∂x3 ∂y ∂x1 ∂z ∂x2 ∂z ∂x3 ∂z
I
αI dxI 上，得到(p + 1)次微分形式： ∂αI i dx ∧ dxI , ∂xi
αI dxI =
i I
其中 dxI ≡ dxi1 ∧ dxi2 ∧ · · · ∧ dxip . 运算∧称为楔积． 运算法则2 因此， dxi ∧ dxi = 0. 运算法则3 设α为p次微分形式，β, γ 是q 次微分形式， d(β + γ ) = dβ + dγ, d(α ∧ β ) = (dα) ∧ β + (−)p α ∧ (dβ ), d(dα) = 0. dxi ∧ dxj = −dxj ∧ dxi ,