地表粗糙度参数化研究综述_江冲亚
- 格式:pdf
- 大小:586.79 KB
- 文档页数:12

地下水环境质量评价——基于粗糙集理论和灰色关联系数矩阵的TOPSIS模型许峰;秦成【摘要】提出用粗糙集(RS)理论的属性约简筛选地下水环境质量评价指标,通过主客观组合赋权确定各评价指标的权重,再利用理想解法(TOPSIS)和灰色关联度相结合的方法确定各样本的相对贴近度,从而建立了地下水环境质量评价的RS-TOPSIS 模型.将RS-TOPSIS模型应用于淮河流域某研究区的地下水环境质量评价,结果表明,13个采样点中水质为Ⅰ类、Ⅱ类、Ⅲ类的采样点各有两个,其余各采样点为Ⅳ类,与未约简指标通过理想解法和灰色关联度相结合的评价模型得出的结果是一致的.【期刊名称】《南水北调与水利科技》【年(卷),期】2015(013)006【总页数】5页(P1097-1100,1109)【关键词】粗糙集;理想解法;灰色关联度;水质评价;淮河流域【作者】许峰;秦成【作者单位】中煤科工集团西安研究院有限公司,西安710054;中煤科工集团重庆研究院有限公司,重庆400039【正文语种】中文【中图分类】P641作为地下水环境保护和治理的一项基础性工作,地下水环境质量评价是进行地下水环境管理的重要手段之一。
随着测试手段和计算技术的发展,水质评价的方法也在日益增多,如:灰色关联法、模糊评判法、层次分析法、人工神经网络法[1-6]。
然而由于地下水环境质量评价指标繁多而带来的评价工作量大、计算复杂、评价主观性强;水质指标信息的如何最大利用以及水质评价中权重的确定,这些都是水质评价工作过程中所要面临和解决的问题。
针对上述问题,本文拟首先利用粗糙集理论中的属性约简方法对评价指标进行筛选,其次利用约简后的指标构成最初的评价矩阵并构造多指标问题的理想解,计算各方案与理想方案的灰色关联系数矩阵,以灰色关联系数矩阵作为新的决策矩阵,再利用TIOSIS法进行方案排序[7-12]。
通过对淮河流域某研究区进行实证研究,得出了比较合理的评价结果。
1.1约简思路水环境质量评价中多指标会导致评价工作的繁杂,因此需要在不影响评价结果的基础上,采用粗糙集理论对水质评价指标进行约简。

表面粗糙度的主要评定参数表面粗糙度是表面几何特征的量化描述,它是评定物体表面的光洁程度或粗糙度的重要参数。
表面粗糙度的主要评定参数有:粗糙度高度参数、波动参数、曲率参数、光谱参数等。
1.粗糙度高度参数:用于衡量表面在垂直方向上的高度差异。
常用的参数有Ra(平均粗糙度)、Rz(十个最大峰值间距平均)和Rq (平均底部谷值深度)等。
Ra是最常用的参数,它表示单位长度上表面高度正负偏离平均值的平均值。
粗糙度高度参数描述表面的平均粗糙度水平和表面上峰谷起伏的平均水平。
2.波动参数:用于衡量表面在平行方向上的高度变化,即表面的波动性。
常用的参数有Wt(材料垂直方向上的峰谷间距离的累积概率函数平方差的开方)和Wm(表面除了比还高和比较低的部分的峰和谷外,其他部分的峰谷间距离平均值)等。
波动参数较好地反映了表面起伏的统计性质。
3.曲率参数:用于描述表面的曲率特性。
常用的参数有Rt(表面曲率的方根的平均值)和RPC(表面法线方向与某一指定方向的夹角的标准差)等。
曲率参数描述表面的弯曲性、蜂窝状程度和不规则程度。
4.光谱参数:用于描述表面的频率成分。
常用的参数有Amplitude-Peak(表面高度变化的最大峰-谷差)、Spectral-Centrod (颜色信息的分布中心)、Slope-RM(表面斜率的均方根的标准差)等。
光谱参数主要从自相关函数、功率谱或相关性配分函数得到,它用于衡量表面上各种高度波动的频率成分。
这些评定参数并不是孤立存在的,它们之间存在关联性。
评定表面粗糙度时,需要综合考虑多个参数的相互作用,以全面、准确地描述表面的粗糙度特征。
同时,不同种类的物体表面可能需要选择不同的评定参数。
例如,在工业领域,常用的评定参数是Ra和Rz;在光学领域,常用的评定参数是RPC和Amplitude-Peak。
总之,表面粗糙度的主要评定参数有粗糙度高度参数、波动参数、曲率参数和光谱参数。
通过综合考虑这些参数的结果,可以更准确、全面地描述表面的粗糙度特征,为工业生产、科学研究等领域提供有力的参考依据。

24卷第17期2005年9 岩石力学与工程学报 Vol.24 No.17 月 Chinese Journal of Rock Mechanics and Engineering Sept.,2005粗糙表面分形维数估算的改进立方体覆盖法张亚衡1,周宏伟1,谢和平12 ,(1. 中国矿业大学(北京) 岩石力学与分形研究所,北京 100083;2. 四川大学,四川成都 610065)摘要:岩石断口表面形貌的定量描述是评价其力学行为的基础。
在粗糙表面分形维数估算的立方体覆盖法基础上,提出了估算粗糙表面分形维数的改进立方体覆盖法。
进一步根据粗糙表面形貌的有关数据,采用立方体覆盖法和改进的立方体覆盖法分别对同一粗糙表面估算其分形维数值,并进行了对比分析,发现改进的立方体覆盖法不仅具有直接覆盖法的优点,其估算过程也更加直观和方便。
关键词:岩石力学;粗糙表面;分形维数;立方体覆盖法;改进的立方体覆盖法中图分类号:TU 311.2 文献标识码:A 文章编号:1000–6915(2005)17–3192–05 IMPROVED CUBIC COVERING METHOD FOR FRACTALDIMENSIONS OF A FRACTURE SURFACE OF ROCKZHANG Ya-heng1,ZHOU Hong-wei1,XIE He-ping12 ,(1. Institute of Rock Mechanics and Fractals,China University of Mining and Technology,Beijing 100083,China;2. Sichuan University,Chengdu 610065,China)Abstract:Description of fracture surface of rock is the base of evaluating its mechanical behavior. Ways to determine the fractal dimensions of a fracture surface are essential for a better understanding of its complete topographic characteristics. Triangular prism surface area method,projective covering method and cubic covering method are three widely used methods at present. Both the triangular prism surface area and projective covering methods cannot avoid the problem of approximate estimation of the real area surrounded by four points on the fracture surface,because the four points considered seldom lie on a plane. Such approximate calculations will certainly result in error. However,the cubic covering method can assure that every step is accurate. Therefore,it can be regarded as a reliable method for direct determination of the fractal dimension of a fracture surface. In this paper,a laser profilometer is employed to measure the topography of a rock fracture surface. Based on cubic covering method for the fractal dimensions of a fracture surface of rock,a new method named improvedcubic covering method is proposed. Cubic covering method and improved cubic covering method are applied to computing fractal dimensions of the same fracture surface of rock. The results show that the improved cubic covering method not only has the advantage of the cubic covering method,but also has more convenient computing process.Key words:rock mechanics;fracture surface;fractal dimension;cubic covering method;improved cubic covering method~多有意义的研究成果[16],但大多数研究成果都是1 引言分形几何在粗糙表面形貌描述领域已取得了很收稿日期:2005–02–24;修回日期:2005–04–17 对粗糙表面上剖线形貌进行分形描述,对整个粗糙表面形貌的分形描述方法较少,有些研究仅限于对一维问题的推广,Mandelbrot本人也提出用剖线的基金项目:国家重点基础研究发展规划(973)项目(2002CB412707);国家自然科学基金资助项目(10372112,50221402);教育部优秀青年教师资助计划项目作者简介:张亚衡(1980–),男,2003年毕业于中国矿业大学北京校区力学与建筑工程学院土木工程专业,现为硕士研究生,主要从事岩石力学方面的研究工作。


粗糙度参数详解范文
所谓粗糙度,指的是物体表面的局部坡度的变化程度,是表面结构形
状特征的重要参数。
粗糙度参数定义了物体表面不同部位的平滑程度,反
映了物体对空气、液体以及其它介质的摩擦力,在传热、润滑、流体传播、接触力、着色、涂覆性等等科学技术领域有广泛的应用。
它根据不同的表面处理技术和表面处理工艺而异,具体表示通常有以
下几种形式:
1)空间波纹度(Spatial waviness):用不同的频率和振幅来表示
表面上有规律性或者无规律性波纹的数量。
2)全表面振幅(Total surface roughness):特征曲线的振幅反映
表面的波动精度,这种粗糙度的参数是通过刻度表或者视觉分析的方式来
判断的。
3)等效粗糙度(Equivalent roughness):对三维表面坡度波动的
综合考量,将复杂的表面粗糙度简化为单个参数,是相对性比较强的参数。
4)长度基函数(Length-base parameter):这是一种能够表示表面
粗糙度的特征参数,根据表面形状的不同,可分为有序类(横向长度参数、纵向长度参数)、无序类(熔點长度、总长度参数)。
5)表面脊线参数(Surface crest parameter):从表面形状的角度
出发,对表面脊线的特征采用直方图统计的方式,以表面纹理的光滑度为
基础。

地表粗糙度对大气湍流产生的影响机制研究引言:地表粗糙度是指地表上表面的不平整程度,包括建筑物、树木、山脉等物体对大气流动的干扰程度。
地表粗糙度对大气湍流产生的影响机制一直是大气科学研究的重要课题之一。
在本文中,我们将探讨地表粗糙度对大气湍流产生影响的机制,并讨论了这一机制的意义和应用。
影响机制:地表粗糙度的存在会改变大气流动的速度和方向,从而对湍流的产生产生影响。
一方面,地表粗糙度会增加乱流产生的机会。
当空气流经粗糙的地表时,扰动会增强,从而刺激大气中的湍流形成。
另一方面,地表粗糙度还可能产生湍流的阻碍效应。
当空气流经粗糙地表时,表面的障碍物会阻碍气流的速度,使得湍流形成的机会减小。
这两种机制共同作用,决定了地表粗糙度对大气湍流产生的影响。
地表粗糙度对大气湍流产生影响的意义:地表粗糙度对大气湍流的产生有着重要的意义。
首先,湍流作为大气中能量和质量传输的核心过程,对大气环境的形成有着重要的影响。
了解地表粗糙度对湍流产生的影响机制,能够帮助我们更好地理解和模拟大气风场的变化,从而提高气象预测和环境管理的准确性。
其次,地表粗糙度对大气湍流的影响还与气候变化和天气现象密切相关。
随着全球气候变暖,地表粗糙度的变化可能导致湍流产生的模式发生变化,从而影响降水和温度的分布。
因此,研究地表粗糙度对湍流产生的影响机制具有重要的应用价值。
地表粗糙度对大气湍流产生影响的实证研究:为了深入了解地表粗糙度对大气湍流产生的影响机制,许多研究者进行了实证研究。
例如,他们使用探空仪和地面观测资料,对不同地表粗糙度条件下的湍流状态进行监测和分析。
研究结果表明,地表粗糙度较高的区域湍流产生的机会更多,湍流强度更大。
此外,还有研究表明,地表粗糙度与湍流强度之间存在一定的非线性关系。
这些实证研究为进一步理解地表粗糙度对大气湍流产生的影响机制提供了重要的参考。
地表粗糙度对大气湍流产生影响的应用:研究地表粗糙度对大气湍流产生的影响机制不仅具有科学意义,而且对相关领域的应用具有重要价值。

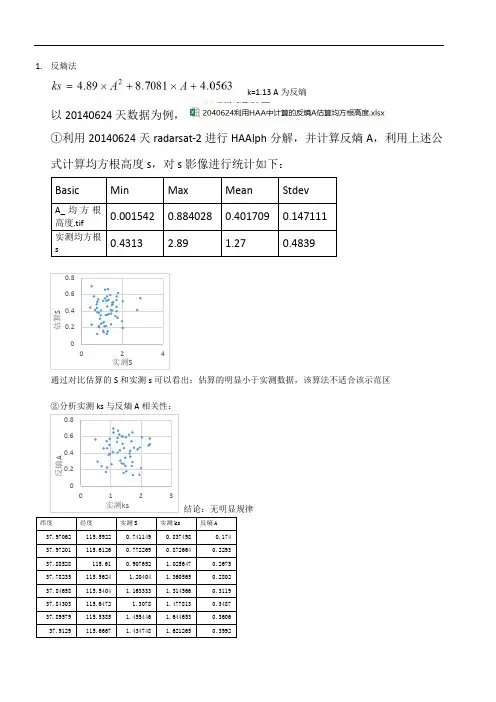
1. 反熵法k=1.13 A 为反熵以20140624天数据为例,①利用20140624天radarsat-2进行HAAlph 分解,并计算反熵A ,利用上述公式计算均方根高度s ,对s 影像进行统计如下:通过对比估算的S 和实测s 可以看出:估算的明显小于实测数据,该算法不适合该示范区②分析实测ks 与反熵A 相关性:结论:无明显规律③引入DEM利用ARCGIS计算地表粗糙度参数地面粗糙度是指在一个特定的区域内,地球表面积与其投影面积之比。
它也是反映地表形态的一个宏观指标。
根据地面粗糙度的定义,求每个栅格单元的表面积与其投影面积之比,可以用如下方法来完成。
假如ABC是一个栅格单元的纵剖面,α为此栅格单元的坡度,则AB面的面积为此栅格的表面积,AC面为此栅格的投影面积(也既是此栅格的面积),根据公式:Cosα=AC/AB则可得出此栅格单元的地面粗糙度M为:M=“AB面的面积”/“AC栅格单元的面积”=(AC*AB)/(AC*AC)=1/Cosα地面粗糙度的提取步骤如下:(1)激活DEM主题,选择Spatial Analysis-Surface Analysis-Slope命令,提取DEM主题的坡度,得到主题Slope of DEM;(2)激活主题Slope of DEM,在Spatial Analysis下使用栅格计算器Calculator,如图20所示,公式为:1/Cos([Slope of DEM]*3.14159/180)分析地表粗糙度参数和反熵A之间相关性:由上图可以看出:反熵A和地表粗糙度、坡度、DEM没有明显的相关性?2.交叉极化比法①以20140627为例,模型高估了均方根高度,不适合该示范区②矫正上述公式,最终获得矫正后公式如下200hv hv 00hhhhks=0.0174*0.383*0.0117⎛⎫⎛⎫++⎪ ⎪⎝⎭⎝⎭对上述公式进行验证:④引入DEM利用ARCGIS计算地表粗糙度参数分析交叉极化与地表粗糙度、slope和dem相关性:分析结果显示:无明显相关性。

表面粗糙度对材料表面超疏水性的影响第1期陈爽等铝阳极氧化膜的硫酸钇脉冲封闭 49 表面粗糙度对硅橡胶材料表面超疏水性的影响周蕊1a金海云1b高乃奎1b彭宗仁1b乔冠军1a李西育2金志浩1a 1.西安交通大学 a金属强度国家重点实验室b电气绝缘国家重点实验室西安7100492.西安高压套管有限公司西安 710077 摘要采用一种简单的方法制备出了硅橡胶超疏水性表面将模具内表面做成一定的粗糙度按照常规成型工艺将液体硅橡胶浇注在模具内使其固化待固化完毕后脱去模具得到不同粗糙度的表面。
经过接触角测量仪测定和扫描电子显微镜分析结果表明当硅橡胶表面粗糙度Ra6.63 ??m时在其表面形成了类似于荷叶的乳突结构在乳突表面还有亚微米级的小颗粒存在形成了微米亚微米两级的粗糙结构材料表面与水的静态接触角为153.5?滚动角为8?材料具有超疏水性当硅橡胶表面粗糙度 Ra6.63 ??m材料表面的静态接触角随着表面粗糙度的增加而减小。
关键词表面粗糙度静态接触角滚动角超疏水中图分类号TB302 文献标识码A 文章编号1007–9289200906–0030–06 Influence of Surface Roughness onSuperhydrophobicity of Silicone Rubber Surface ZHOU Rui1 JINHai??yun2 GAO Nai??kui2 PENG Zong??ren2 QIAO Guan??jun1 LI Xi??yu3 JIN Zhi??hao 1a. State Key Laboratory for Mechanical Behavior of Materials b. State Key Laboratory of Elect rical Insulation and Power Equipment Xi’an Jiaotong University Xi’an 710049 2. Xi’an High??pressure Casing CO LTD Xi’an 710077 Abstract: In this paper we report on a simple method to prepare superhydrophobic surface on silicone rubber. Different surface roughness was formed along the mold inner surfaces. Then the liquid silicone rubber was molded in the mold with the standard molding processing. After consolidation was accomplished completely and the mold was released surface with different roughness was obtained. By exterminating contact angles and scanning electron microscopyobservation we found when the roughness of the surface Ra was 6.33 μm a similar mastoid microstructure with lotus leaves was formed on the silicone rubber surface. There were some sub–micron particles on the mastoid. Micron and sub–micron rough structures wereformed. The static contact angle obtained was 153.5? and the rolling angle was 8?. When the surface roughness Ra was less than 6.63 ??m the static surface contact angle increases with the surface roughness increasing when the surface roughness Ra was 6.63 ??m the static contact angle was largest. The maximum value was 153.5?. When the surface roughness Ra was more than 6.63 ??m surface static contact angledecreases with the surface roughness increasing. Key words: surface roughness static contact angle rolling angle super hydrophobic0 引言硅橡胶绝缘子因其重量轻、机械强度高、表面憎水性强、耐污闪能力强、制造维护方便等优点在全国35500 kV交直路中得到广泛应用。

参数解说介绍参数概述表面纹理可由与一定的纹理特性相关的参数来量化。
这些参数可按测量的特点类型,被分成几组类型。
它们是:Amplitude(幅值)Spacing(间距)Hybrid(混合)R&W(R+W)Aspheric(非球面)曲线及相关参数Rk 参数影响表面粗糙度的数字评估是三个特性长度。
它们是:取样长度,也被称为Cut-Off Length评价长度,也被称为Assessment Length或Data Length横向移动长度另外,屏幕上的帮助工具,以一个容易阅读的Exploring Surface Texture(表面形貌浏览)文本描述,其主题详细包括了什么是表面形貌及为什么必需测量它。
该文本包括用Form Talysurf仪器提供通常的表面形貌背景信息和测量仪器的特殊测针类型。
它也给出了参数的有用信息:它们的来历和使用。
对进一步更深的表面评论及其测量,可从Taylor Hobson的手册Precision 2中得到。
幅值参数这些是测量在轮廓(Z轴)的垂直位移。
这类参数包括:未滤波参数滤波的粗糙度参数滤波的波纹度参数间距参数这些参数是沿表面(X轴)对不规则间距的测量,而与不规则的幅值无关。
这类参数包括未滤波参数滤波的粗糙度参数滤波的波纹度参数混合参数指与表面不规则的幅值参数和间距参数都有关的参数(Z轴和X轴),或者规定了一个量,如面积或体积,被称作Hybrid(混合)参数。
这类参数包括:未滤波参数滤波的粗糙度参数滤波的波纹度参数曲线及相关参数这些参数是沿表面(X轴)对不规则间距的测量,而与不规则的幅值无关。
这类参数包括:原始轮廓轮廓高度幅值曲线PcPmrPmr(c)滤波的粗糙度轮廓高度幅值曲线RcRmrRmr(c)滤波的波纹度轮廓高度幅值曲线WcWmrWmr(c)R加W 参数这些参数与R和W参数相关,被定义在标准BS ISO 12085:1996里面。
这些分析包括:PtRARRxSRSARSWSAWWteWAWWx非球面分析参数这些参数与非球面形状的特殊分析有关。

PolInSAR地表参数反演方法研究的开题报告一、选题背景与意义随着雷达技术的不断发展和应用,PolInSAR(Polarimetric Interferometric Synthetic Aperture Radar)技术作为高分辨率、全天候、无死角的遥感技术广泛应用于地表覆盖分类、地形高程模拟、测量物体高度、植被生物量估算等领域,已经成为雷达遥感领域的热点和前沿。
在PolInSAR技术中,利用空间多角度雷达数据(Polarimetric SAR data)和SAR干涉数据(Interferometric SAR data),可以获取部分地形、林木高度等地表参数信息。
然而,这些地表参数可能在复杂的林区、湿地、山地等地形背景下存在不确定性,亟需深入的研究和探索。
因此,基于PolInSAR技术的地表参数反演方法研究具有重要的实际意义和开发前景。
二、研究现状和分析PolInSAR技术中,主要的地表参数包括地形高程、林木高度和植被生物量等。
目前,对于其中的地形高程信息,已经有较为成熟的理论模型和方法,如双基线干涉合成孔径雷达(InSAR)技术、高程反演模型等;而对于林木高度和植被生物量等地表参数,尚需进一步探索和研究。
其中,针对林木高度信息反演,比较广泛的方法是多基线PolInSAR技术,该方法需要获取尽可能多的SAR数据,通过多个SAR波频比较,获得更加丰富的林木高度信息;至于植被生物量信息反演,研究较为困难,目前尚处于初步探索阶段。
三、研究内容和方案本课题拟中心探索和研究利用PolInSAR技术反演林木高度和植被生物量信息的方法。
具体来说,将主要从以下两个方面展开研究:1.林木高度地表参数反演:研究多基线PolInSAR反演林木高度信息的方法,探索数据处理和模型求解的最优组合方案,进而提高林木高度信息的精度和可靠性;2.植被生物量地表参数反演:研究各类雷达信号与植被生物量的关系,建立植被生物量反演模型,探究模型求解的可行性和有效性,提高植被生物量信息的获取精度和全面性。
岩体结构面粗糙度系数定量表征研究进展陈世江;朱万成;王创业;张飞【摘要】The joint roughness coefficient (JRC) method was suggested by International Society for Rock Mechanics to estimate joint roughness in 1978. Although this method is widely used in engineering practices, there is a shortcoming of subjectivity and experience relied on investigator. So, the research works about quantifying joint roughness were devel-oped by authors in the world. In this article, firstly, we introduced the research progress about quantitative characterization on both joint profiles and discontinuities roughness,and summarized the results of relationship between the parameters and JRC. Secondly, we evaluated the essential properties and applicability of each parameter, pointed out the problems about the parameters in obtained process including sampling interval influence, deciding triangulation of an elementary surface and determining the weight of each parameter in the comprehensive parameters method. At the same time, we gave the author's ideas of solving the problems. In addition, we discussed anisotropy and size effect of surface roughness in detail, on which are focused by researchers. Finally, we predict that fractal dimension remain a method to describe surface roughness and 3D printing technology can be helpful to research anisotropy and size effect of rock discontinuities roughness.%1978年,Barton提出的节理粗糙度系数(joint roughness coefficient,JRC)被国际岩石力学学会作为评估节理粗糙度的标准方法.然而该方法存在人为估值的主观性缺陷.就此,国内外学者围绕岩体结构面粗糙度定量化表征开展了大量的研究工作.首先,从二维节理轮廓线到三维岩体结构面,系统地阐述了其粗糙度定量化表征方法研究进展,并总结了各方法参数与JRC的关系;评价了各表征参数的本质特性及其适用性;指出了各方法参数获取过程中存在的问题,主要有:采样间隔的影响,三角形单元划分的影响,如何确定综合参数法中各参数的权重;针对这些问题,给出了笔者的一些想法、建议.与此同时,对结构面粗糙度表征的两个热点问题,即各向异性和尺寸效应的研究也进行了详细总结分析.最后,笔者认为:(1)分形维数因是描述自然界复杂几何体的一种简洁有力的工具,其仍是结构面粗糙度定量描述的有效方法;(2)3D打印技术的应用,有望在开展结构面各向异性、尺寸效应研究方面取得突破性进展.【期刊名称】《力学学报》【年(卷),期】2017(049)002【总页数】18页(P239-256)【关键词】岩石力学;岩体结构面;粗糙度;研究进展【作者】陈世江;朱万成;王创业;张飞【作者单位】内蒙古科技大学矿业研究院,内蒙古包头014010;东北大学资源与土木工程学院,沈阳110819;内蒙古科技大学矿业研究院,内蒙古包头014010;内蒙古科技大学矿业研究院,内蒙古包头014010【正文语种】中文【中图分类】TD325粗糙度是岩体结构面力学性质的重要影响因素.诸如结构面的剪切强度、节理裂隙的渗流特性均与结构面的粗糙度有着密切的关系.1973年Barton[1]通过试验推导了岩体结构面峰值剪切强度经验公式,首次提出了节理粗糙度系数 (joint roughness coefficient,JRC),用于定量描述结构面的粗糙度.1977年Barton等[2]通过对 136个岩石试件剪切试验的研究,给出了十条典型节理轮廓线,用来评估JRC值,其取值范围在0到20之间,见表1.1978年国际岩石力学学会将该方法作为评估节理粗糙度的标准方法[3].虽然,JRC在工程实践中得到广泛应用,但其存在人为估值的主观性缺点,在实际应用中不够客观准确[4].因此,近半个世纪以来,国内外学者围绕岩体结构面粗糙度定量化表征这一课题开展了大量的研究工作,并取得了丰硕的研究成果.围绕结构面粗糙度定量化表征方法,本文重点开展了如下8个方面的综述工作:(1)二维节理轮廓线粗糙度定量化表征;(2)三维结构面粗糙度定量化表征;(3)岩体结构面粗糙度各向异性特征描述;(4)岩体结构面粗糙度尺寸效应特征描述;(5)岩体结构面形貌信息数据获取方法研究进展;(6)结构面粗糙度定量化表征参数本质特性及其适用性评价;(7)各表征参数获取过程中的影响因素分析与相关解决方案的粗浅想法;(8)结构面粗糙度研究发展方向的粗浅认识.从目前的研究成果看,在二维节理轮廓线粗糙度定量化表征方面,主要有统计参数、分形维数、综合参数及直边图解4种描述方法.然而,二维节理轮廓线粗糙度不能代表三维结构面的粗糙特性,鉴于此,学者们在结构面定量化表征方面做了深入研究,主要成果有:Z2s,Rs,θs,F(θ),BAP,JRCv及SRv表征法、分形维数表征法.实际上,岩石结构面力学性质是存在各向异性和尺寸效应的,而这一性质主要源于结构面粗糙度特征.目前,结构面粗糙度各向异性和尺寸效应特征是该研究领域的热点,本文对此也进行了详细总结分析.表征岩体结构面形貌特征参数获得的前提是结构面形貌信息数据的量测.从大量文献可知,该获取方法主要为接触式量测和非接触式量测,而非接触式量测方法中,三维激光扫描技术目前被广泛使用.这一课题,成果丰硕,但也存在缺陷.因结构面形貌的复杂性,目前,仍没有一个参数能够很好地表征其粗糙特征.另外,各表征参数计算过程中,采样间隔、三角形单元划分、综合参数法中各参数权重的确定是相关参数获取过程中存在的主要问题.通过分析,笔者也给出了相关问题的粗浅解决方法.总之,通过对岩体结构面粗糙度研究进展的总结归纳,以期为从事该课题研究的相关学者提供参考.最后,笔者认为,分形维数是描述自然界复杂几何体的一种强有力的工具,且在计算过程中与其他参数有本质区别,因此,该法仍是评价结构面粗糙度的有效方法;3D打印技术的应用可有效解决岩体结构面不可重复试验的问题,因此,应用此技术,结构面各向异性、尺寸效应的研究有望有新的突破.1.1 JRC2D定量表征方法综述1.1.1 统计参数描述法1.1.1.1 起伏幅度表征法起伏幅度表征法是以贯穿于节理轮廓线的一条基准线为基础,研究其起伏幅度特征,进而表征其粗糙度,如图1所示.该方法的主要特征参数有[5-6]:均方值MS,均方根RMS,中心线平均值CLA,一阶导数均方根(Z2),二阶导数均方根(Z3),区分坡向特征的起伏幅度均值参数(Z4),自相关函数ACF和结构函数SF.各参数表达式见式(1)~式(8).式(1)~式(8)中:L为表面轮廓线总长度;y和f(x)均表示表面轮廓线幅度;∆xi和Dx均为L上的一个单元分段;(∆xi)p为轮廓线正向坡的长度;(∆xi)n为轮廓线负向坡的长度.对于参数MS,RMS,CLA,Z4及ACF,基准线位置是影响其结果的重要因素.为了消除这一影响,文献[5]给定的基准线称为中心线,该中心线与轮廓线围成的上下部分面积相等.然而,在实际操作过程中,寻找这条中心线是比较困难的.而参数Z2,Z3和SF研究的是节理轮廓线线上两点起伏差的特征,如图1所示.因此,参数Z2,Z3和SF不受基准线的位置的影响.1979年,Tse和Cruden[5]采用参数MS,RMS,CLA,Z2,Z3,Z4,ACF和SF对Barton标准轮廓线进行了定量化研究,分别建立了各参数与JRC的函数关系式.通过分析,参数Z2,SF与节理粗糙度系数(JRC)的相关度最高,其函数关系式为2001年,Yang等[7]对式(9)和式(10)的推导过程进行了深入研究,发现Tse等[5]在建立Z2,SF与JRC的关系时,将十条标准轮廓线在x轴和y轴方向上分别同时扩大了2.5倍(长度上由原来的10cm扩至25cm).对于自仿射节理轮廓线来说,这样的预处理将改变其本身的形貌,是不恰当的.鉴于此,Yang等[7]采用傅里叶变换方法,重建了10条标准节理轮廓线,然后计算了其一阶导数均方根Z2和结构函数SF,最后采用回归分析法给出了Z2和SF与JRC的函数关系式事实上,节理轮廓线正反两向的剪切力学性能是不同的.这主要源于其正反两向粗糙度的不同.基于这一认识,Zhang等[8]将参数Z2进行了改进,其改进的表达式为1.1.1.2 起伏角表征法1991年,Yu等[9]介绍了用起伏角标准差SDi描述节理轮廓线粗糙度的方法,并研究了参数SDi在0.25mm,0.5mm,1mm采样间隔下与JRC的关系.考虑结构面剪切方向,Belem等[10]提出用坡度统计参数Sp+,Sp-描述节理轮廓线粗糙度.如图2所示.图2中,Sp+为平均正向坡度参数,用θp+表示,Sp-为平均负向坡度参数,用θp-表示.式中,Mx+和Mx-分别表示节理轮廓线长度范围内间隔为∆x时的正向坡度(∆z/∆x)+的总数及负向坡度(∆z/∆x)-的总数.对于参数Z2,其近似计算公式[5]为从式(20)可以看出,参数Z2表面上研究的是节理轮廓线起伏幅度特征,实质上表征的是节理轮廓线的平均起伏角.这一点,文献[8]也进行过分析.1.1.1.3 迹线长度表征法1978年,EI-Soudani[11]提出了用Rp表示物体的线粗糙度.Rp为迹线长度与其直线长度的比值,表达式为从式(21)可知,Rp大于1时,意味着节理轮廓线是粗糙的;其值越大,越粗糙. Maerz等[12]应用上述方法,在十条标准轮廓线数字化的基础上,计算了每条节理轮廓线的Rp值,最后给出了JRC与Rp的关系为1991年,Yu等[9]也计算了十条标准轮廓线的Rp值,研究了不同采样间隔下Rp 与JRC的关系.同时也建立了不同采样间隔下(Rp-1)与JRC的函数关系式,相关公式见表2.通过比较分析,认为参数(Rp-1)与JRC的函数关系更为密切.对于参数Rp,王建峰[13]、杜时贵等[14]指出该参数表达的物理意义不明确.陈世江等[15]认为该参数物理意义不明确的原因在于节理轮廓线在不同幅值下所测得的Rp是没有可比性的.笔者考虑了节理形态的层次性,用参数Rp代表节理的次级精细结构,用节理轮廓线的起伏度表示节理的一级波状形态,给出了参数Rp,ε(起伏度)与JRC的关系1.1.2 分形几何描述法20世纪70年代,Mandelbrot[16]创立分形几何,因其是研究自然界中不规则几何体的一种极其有效方法而受到众多学者的青睐.在应用分形维数描述节理轮廓线粗糙度方面,大多数学者通过码尺法和计盒数法直接量测获取节理轮廓线分形维数,进而建立与JRC的关系.为克服分形维数量测上的困难,谢和平[17]提出了一个节理分形模型 2h∗/L∗,该模型为式中,L∗和h∗分别为节理轮廓线平均基长和平均高度.通过量测L∗和h∗即可获得节理分形维数,进而建立节理分形维数与JRC的关系.应用上述3种分形计算方法,国内外学者在节理分形表征方面,做了大量的研究工作,成果显著.相关研究成果见表3.1.1.3 综合参数描述法1.1.3.1 多参数分维联合表征法因节理轮廓线形貌的复杂性,用一个分形维数参数无法全面表征其形貌粗糙特征,因此,一些学者尝试用几个参数综合起来描述岩体结构面的粗糙特征.Kulatilake等[34-35]提出了复合参数Dr1d×Kv表征结构面的粗糙度,其中Dr1d 表示结构面的分形维数(把结构面离散为许多条二维节理轮廓线,用变异函数求解轮廓线分形维数,然后取平均值),Kv是和分形维数Dr1d相关的一个常数.基于岩体结构面表面形貌并不属严格自相似分形,而是具有自仿射分形性质的考虑,Fardin等[36-37]、徐磊等[38]用分形维数D和振幅参数A两参数共同描述了结构面的粗糙特征.基于Grasselli等[39]、Re等[40]和Belem等[10]的研究成果,孙辅庭等[41]考虑岩石节理的主要形貌特性(平均起伏度、起伏的方向性、起伏的分布特点以及粗糙的分形特性),提出了剪切粗糙度综合指标表示分形粗糙度;Dθ+表示分形粗糙度维数;a表示结构面起伏分布特征参数.其中为沿剪切方向为正的起伏角平均剪切抵抗角,可以描述节理的平均起伏程度及其方向性,也可反映节理的整体倾斜,均为分形参数,由公式来确定,∆为测量尺度.文献[41]通过分析十条标准轮廓线,给出了SRI与的关系式,见式(28),并拟合出了SRI与JRC的表达式,见式(29)和式(30)基于Yang等[42]对节理的认识,即节理轮廓线的复杂形态由小规模的细微粗糙结构和大规模的波状起伏结构所构成.陈世江等[43]提出了用分形维数D和起伏度Wd两个指标来描述JRC,即用分形维数代表节理的次级精细结构;用起伏度表示节理的一级波状形态,并给出了参数D,Wd与JRC的关系1.1.3.2 其他综合参数表征法2011年,唐志成等[44]从结构面坡度起伏是影响抗剪强度的主要因素的角度出发,提出结构面“角度粗糙度”的概念;同时认为剖面线长度对粗糙度也是有贡献的,故对二者进行加权处理,采用加权均值与加权方差描述“角度粗糙度”式中θR为角度粗糙度;λ为加权系数,反映微元段长度对角度粗糙度的影响,li和Lt分别为剖面线微元段长度、剖面线实际长度;和θv分别为平均方位角、方位角方差.2014年,李化等[45]在充分考虑工程结构面起伏形态的实际测量条件基础上,提出利用相对起伏度Ra和伸长率R共同反映结构面粗糙度系数JRC,建立了JRC与Ra,R两个因素的经验公式.当0≤JRC≤8时当8≤JRC≤16时当16≤JRC≤20时2014年,Zhang等[8]对参数Z2表征节理轮廓线粗糙度做了深入研究,发现参数Z2仅仅表示的是节理轮廓线的平均倾角,而不能够描述其起伏幅度.于是提出了一个综合参数λ表征节理轮廓线的粗糙度,并给出了参数λ与JRC的函数关系式中为改进的Z2,h为节理轮廓线最大起伏高度,L为节理轮廓线长度.1.1.4 直边图解法上述统计参数、分形维数及综合参数表征法主要解决了节理轮廓线定量化描述的问题.然而,现场节理长于或远长于10cm,如何用Barton十条标准轮廓线准确估测工程节理粗糙度是摆在技术人员的一个难题.早在1982年,Barton和Bandis[46]为了解决这一问题,提出了直边法概念,如图3所示.该方法是根据不同取样长度结构面表面轮廓曲线的幅度来确定粗糙度系数JRC.根据200多组结构面统计分析得出了确定JRC值的经验公式式中,Ry为剖面最大起伏幅度,L0实验室结构面轮廓曲线长度,取0.1m,Ln为结构面轮廓曲线长度.杜时贵等[47]利用小浪底节理表面粗糙度系数统计测量资料对直边法进行了检验,指出,对于起伏度为毫米级的岩体结构表面形态而言,直边法的测量精度可以满足岩体结构面表面粗糙度系数的测量要求.同时还发现,直边法中的JRC有可能大于20.基于这一工程实践,杜时贵等[47]改进了直边法,推导了修正直角边法的数学表达式1.2 JRC3D定量表征方法综述1.2.1 Z2s表征法参数Z2可以较好量化节理轮廓线的粗糙度.然而,用节理剖面线的粗糙度代表结构面特征是片面的.Belem等[10]考虑结构面的三维特征,提出了参数Z2s描述法.该参数Z2s在假设结构面上各点连续可微,可定义为1.2.2 Rs表征法1978年,EI-Soudani[11]提出了用Rs表示物体的面粗糙度.Rs可用式(42)表示式(42)和式(43)中,At为结构面表面实际面积;An为结构面投影面积;Ai为结构面单元的实际面积,可用图4来表示.2009年,Tatone等[48]采用Rs表示结构面粗糙度的方法研究计算了经三点弯曲破裂后的4个混凝土梁断面的Rs值,研究区域大小为150mm×150mm,见图5.计算结果分别为1.09,1.10,1.18,1.24.1.2.3 θs表征法2000年,Belem等[10]提出了用平均倾角θs表示三维结构面的粗糙度.首先将结构面离散为m个单元平面,如图6,单元平面的法向量与z轴方向夹角为该单元平面的倾角,记为ak,则1.2.4 F(θ)表征法考虑岩体结构面具有各向异性特征,Aydan等[49]提出了形貌函数F(θ)描述法角度θ的确定,如图7所示,顺着结构面主沟槽或主突起的方向为x轴,正交于x 轴的方向为y轴,沿x轴方向逆时针旋转的角度为θ角.1.2.5 表征法基于只有面向剪切方向的节理微元才对节理剪切力学行为产生作用的这一事实,Grasselli等[39]提出了剪切方向有效接触面积比和剪切方向倾角θ∗的概念,并给出了其关系表达式式中,Aθ∗为≥θ∗的微元面积的总和与节理表面总面积的比值;A0为最大可能接触面积比;为最大剪切方向倾角;C为节理表面粗糙度参数.剪切方向倾角θ∗可用式(47)进行计算其中,θ∗,θ,a位置关系如图8所示.在上述研究的基础上,Grasselli计算了6种岩石表面的值,结果表明,组合参数能够表征节理表面的粗糙度.该组合参数值小意味着结构面较光滑,值大表示结构面较粗糙.Grasselli等[50]进一步通过变角剪切试验,证实了参数不仅可以表征节理面的粗糙度,还可以表征节理面形貌各向异性特征.同时,认为在剪切过程中,结构面上凸体的破裂主要为拉伸破坏;以此为基础,通过对37个节理试件的剪切试验数据回归分析,给出了参数与JRC的函数关系式.若岩体结构面未遭风化时,JCS=σc,σc为岩块单轴抗压强度.后来,Tatone等[48]进一步研究了指出该参数仅仅是一个表征结构面粗糙度的经验参数,没有明确的物理意义;并且在特殊情况下,如节理面为规则的锯齿形结构面时,为常数,即这样,C=0,这时结构面粗糙度参数将失去意义.鉴于此,Tatone经过严密的数学推理,提出了用参数表示结构面剪切方向平均倾角.用该参数表征结构面粗糙度,其物理意义明确,且在上述特殊情况下其值存在.2010年,Tatone等[51]通过研究十条标准轮廓线,给出了不同采样间隔下与JRC的函数关系式.采样间隔为0.5mm时采样间隔为1.0mm时2014年,Jang等[52]也研究了参数与JRC的关系,给出了采样间隔为 0.5mm时,与JRC的关系1.2.6 BAP表征法2012年,葛云峰等[53-54]考虑结构面粗糙度系数的三维特性和各向异性特征,提出基于光亮面积百分比BAP的岩体结构面三维粗糙度系数表征新方法,并给出了在光源入射角为55°,灰度阈值为140时,BAP与JRC的关系1.2.7 JRCv及SRv表征法2015年,陈世江等[55-56]考虑岩体结构面的地质本质性[57],研究了结构面粗糙度的各向异性特征;应用地质统计学原理[58],提出了采用变异函数参数(基台C和变程a)表示结构面粗糙度(JRCv)的方法.通过量纲分析法给出了JRCv的表达式结果表明,参数JRCv可以很好地反映结构面粗糙度的各向异性特征.最近,陈世江等[59]重新审视了JRCv描述结构面粗糙度全面性后,提出了一个考虑各向异性特征的综合参数SRv表征岩体结构面粗糙度的新方法.λ由某一方向的起伏角参数SRv和起伏幅度参数A表示.通过计算Barton十条标准轮廓线的起伏角SRv和起伏幅值A两参数,拟合出了考虑各向异性特征的结构面粗糙度定量估算公式式中,A为结构面平均起伏幅值系数,可用结构面的平均起伏高度与其长度的比值来表示表示结构面的平均起伏角,用公式进行计算;a为常数,根据Zhang等[8]的研究,其值为1/3.1.2.8 分形维数表征法为了克服用二维节理轮廓粗糙度表示结构面粗糙特征的不足,尹红梅等[60]自行研制了结构面形态三维量测设备,对结构面表面形态进行三维测量,采用立方体覆盖法对结构面进行了分形维数估测,在大量硬性结构面剪切试验的基础上,推导了结构面粗糙度与分形维数的关系陈世江等[61]研究了三维结构面的分形特征,开发了基于数字图像处理技术的岩体结构面投影覆盖法[62-63]分形维数计算程序.通过实例计算,结果表明:结构面形貌是多层次的,具有多重分形的特征.在此基础上,通过石膏试件剪切力学试验数据分析,结合Barton节理峰值抗剪强度公式,给出了JRC分别与多重分形参数∆a(q)和∆D(q)的线性关系岩体结构面粗糙度是存在各向异性特征的,国内外学者早已对此特征进行过关注,并提出了诸多参数用于结构面粗糙度各向异性的描述.如Aydan等[49]在卡迪尔坐标系中提出了与方向倾角θ有关的结构函数F;Yang和Lo[64]基于分形布朗运动理论,用Hurst指数H来描述结构面粗糙度的各向异性特征;Babanouri等[65]用分形维数D和标准差函数σ来表征结构面的各向异性特征.然而,上述参数局限于结构面剖面轮廓线的描述.考虑结构面的三维特性,Yang等[66]用二维Hurst指数H2D描述了结构面的各向异性特征;Kulatilake等[34-35]提出了复合参数Dr1d×Kv表征法;Grasselli等[50]提出一种新的描述结构面粗糙度特征的方法,采用分析了岩体结构面各向异性特征,为沿结构面剪切方向上的最大倾角,C为结构面粗糙度系数;Tatone等[51]进一步研究了参数的物理含义,提出了用描述结构面的各向异性特征.在国内,周宏伟等[67]用累计功率谱密度指数描述节理表面形貌中大尺度上的起伏和小尺度上的涨落,定量地表征了岩体节理表面的各向异性;李久林等[68]用结构面不同方向上剖线的粗糙度研究了结构面的各向异性;杜时贵等[69]用统计的方法,分别计算了结构面不同方向上的JRC值,对比分析了结构面粗糙度的各向异性特征.最近,借助三维激光扫描技术,葛云峰等[53-54]提出了表征结构面粗糙度各向异性特征的BAP法.笔者考虑岩体结构面的地质本质性,应用地质统计学原理,提出了表征结构面粗糙度各向异性特征的JRCv法和SRv法.图9是参数SRv表征结构面粗糙度各向异性的效果图[56],此图没有考虑结构面同一方位正反两向粗糙度的不同.通过上述总结分析,能够描述这一特征的主要方法有:分形维数表征法、表征法、BAP表征法、SRI表征法、JRCv和SRv表征法等.应用分形维数表征结构面粗糙度各向异性特征的研究成果主要集中于二维节理轮廓线的分形描述上.从目前三维结构面分形维数计算方法研究上来看,分形维数很难体现各向异性特征.最近,文献[70]提出一种新的基于三维均方根抵抗角的节理面粗糙度分形计算方法,应用该法计算的分维数可以表征结构面的各向异性特征.该方法为分维数描述结构面各向异性特征提供了一个新思路.岩体结构面不仅具有各向异性特征,而且还有尺寸效应特性.早在Barton和Choubey[2]研究岩体结构面剪切强度时,就对结构面尺寸效应进行过相关论述,即随着岩石节理长度的增大,节理粗糙度系数在减小.之后,Barton和Bandis[46]给出了估计结构面粗糙度系数JRC的尺寸效应修正公式.杜时贵[71]用修正直边法对简易纵剖面仪现场绘制的齐溪二级电站1668条结构面表面轮廓曲线进行JRC 估测,结果发现,取样长度由10cm增大到3m,JRC由15.6下降到5.2,这一事实说明JRC存在明显的尺寸效应.后来,杜时贵等[47]在直边法估计JRC的基础上,给出了考虑尺寸效应的JRC修正直边法数学表达式.Fardin等[36-37]应用分形维数描述了结构面的粗糙度,并详细讨论了结构面粗糙度的尺寸效应,研究结果表明,随着结构面尺寸范围的增大,分形维数在逐渐减小,当增大到一定尺度,分形维数接近一个常数.徐磊等[38]在非接触光栅投影照相式三维测量系统精确获取人工张裂法制备的花岗岩结构面形貌参数的基础上,计算了三维结构面形貌的自仿射分形参数,结果表明,岩体结构面三维表面形貌具有明显的尺寸效应,在一定的尺寸范围内,随着结构面尺寸的增大,其分形参数D、A的值逐渐减小,但当结构面尺寸达到210mm后,分形参数值趋于稳定,不再随尺寸增大而发生明显的变。
专利名称:一种全球高分辨率每日地表动量粗糙度长度估算方法
专利类型:发明专利
发明人:唐荣林,彭中,姜亚珍
申请号:CN202011628578.3
申请日:20201230
公开号:CN112733906A
公开日:
20210430
专利内容由知识产权出版社提供
摘要:本发明涉及一种全球高分辨率每日地表动量粗糙度长度估算方法,它包括数据的获取、对数据进行预处理、构建数据库、计算每日地表动量粗糙度长度、构建全球尺度地表动量粗糙度长度随机森林模型的训练数据集、估算模型并使用该模型生产每日全球尺度地表粗糙度长度产品。
发明旨在解决目前没有全球尺度地表动量粗糙度长度遥感产品的空缺,可准确反映真实的地表动量粗糙度长度的算法模型,有助于提升全球陆表、水文、气候模型精度。
申请人:中国科学院地理科学与资源研究所
地址:100000 北京市朝阳区大屯路甲11号
国籍:CN
代理机构:成都熠邦鼎立专利代理有限公司
代理人:曾克
更多信息请下载全文后查看。
粗糙度rpc -回复什么是粗糙度RPC?粗糙度(Roughness)RPC是一种用于描述表面粗糙度的测量方法,其中RPC代表着反射率配置比值(Reflectance Panel Contrast)。
它是一种光学测量技术,通过测量光线在物体表面的反射率配置比值,来衡量物体表面粗糙度的程度。
粗糙度RPC广泛应用于工程、科学和制造领域,以提供对材料表面的定量评估和比较。
粗糙度RPC的原理粗糙度RPC基于物体表面的反射率配置比值。
表面粗糙度是指微小凸起和凹陷构成的表面几何形貌,它会引起光线在物体表面的反射时发生散射。
粗糙度RPC利用高质量的光源和光谱分析技术,测量物体表面上不同位置处的反射率配置比值。
通过对比不同位置处反射率配置比值的差异,可以确定物体表面的粗糙度。
粗糙度RPC的步骤1. 准备工作:首先,需要选择适当的光源和光谱分析仪器。
高质量的光源能提供稳定且均匀的光照条件,而光谱分析仪器则能测量不同波长下的反射率配置比值。
2. 标定:在进行任何测量之前,需要对光源和光谱分析仪器进行标定。
标定的目的是确保测量结果的准确性和可重复性。
3. 准备样品:选择要测量的样品,并确保其表面光洁、干净、无污染。
对于不同类型的样品,可能需要采用特殊的处理方法,如去除表面涂层或抛光,以确保准确测量。
4. 测量:将样品放置在光源和光谱分析仪器之间,使其表面与光源正交。
通过调整光源的位置和角度,确保光线正好垂直射向样品表面,以最大限度地减少散射。
5. 记录数据:使用光谱分析仪器测量不同位置处的反射率配置比值。
记录每个位置的测量结果,并确保按照相同的方法和顺序进行测量,以保持一致性。
6. 数据分析:根据测量数据,计算样品表面的粗糙度。
通常使用统计方法,如平均值、标准差和变异系数等,来描述粗糙度的程度。
7. 结果解释:根据数据分析结果,可以比较不同样品的粗糙度。
较高的反射率配置比值表明样品表面较为光滑,而较低的反射率配置比值则表明样品表面较为粗糙。
农田粗糙度相关长度与均方根高度的关系概述说明引言部分的内容应该是对整篇文章的概述和介绍,包括文章结构和目的。
以下是清晰撰写的引言部分内容:1. 引言1.1 概述本文旨在研究农田粗糙度相关长度与均方根高度之间的关系。
农田粗糙度是指农田表面的不平坦程度或起伏,常用于土壤侵蚀、水资源管理以及作物生长等领域的研究。
粗糙度特征主要包括相关长度和均方根高度,它们与土地表面形态和水文过程密切相关。
通过研究其关系,可以更好地理解农田表面特征对水文过程和作物生长的影响。
1.2 文章结构本文共包含五个部分。
首先,在引言中概述了研究背景和动机,明确了本文的目标;其次,在"农田粗糙度相关长度与均方根高度的关系"一节中,介绍了农田粗糙度及其测量方法,并探讨了与长度相关的粗糙度特征以及它们与均方根高度之间的演化过程;第三部分是"实验设计和数据收集",详细描述了本研究的实验设置、农田选择标准、数据采集和处理方法以及统计分析方法;接下来,在"结果及讨论"一节中,展示了农田粗糙度与相关长度的关联性分析结果,并推断验证了农田粗糙度与均方根高度之间的关系,并对其他影响因素进行了讨论;最后,在"结论与展望"一节中,总结全文主要发现,并提出存在问题以及未来的研究方向展望。
1.3 目的本文旨在深入探讨农田粗糙度相关长度与均方根高度之间的关系,并通过实验设计和数据收集来验证这种关系。
同时,通过对结果进行讨论和分析,提供有关农田表面特征对水文过程和作物生长影响的科学依据,并为相关领域的研究提供参考。
同时也希望本文可以激发更多的研究兴趣,促进农田粗糙度相关长度与均方根高度之间关系方面的深入探索。
2. 农田粗糙度相关长度与均方根高度的关系2.1 农田粗糙度的定义和测量方法农田粗糙度是指土地表面不平整的程度,它反映了土地表面起伏的大小。
农田粗糙度通常通过测量土地表面的特征来进行评估。
生态学报2010,30(11):2819—2827Acta Ecologica Sinica稀疏植被区空气动力学粗糙度特征及遥感反演张杰1,3,黄建平3,张强2,3(1.气象灾害省部共建教育部重点实验室南京信息工程大学,南京210044;2.中国气象局兰州干旱气象研究所,兰州730020;3.兰州大学大气科学院,兰州730020)摘要:应用中国西北半干旱区定西试验站2005年观测资料,估算了典型的稀疏农作物区空气动力学粗糙度,结合空气动力学模型分析了稀疏植被区空气动力学粗糙度的时间变化及其与风速、植株密度的关系,并得出空气动力学粗糙度的参数化方案;结合卫星遥感得到的植被叶面积指数资料,模拟了区域空气动力学粗糙度,得出:(1)空气动力学粗糙度的时间变化与风速变化规律有相反的特点;在稀疏植被区,粗糙单元分布密度对流场有一定影响,随粗糙单元密度的增加,空气动力学粗糙度将逐渐增大。
(2)植株高度超过0.2m时,植被高度和植株密度、叶面积指数对空气动力学粗糙度的影响较大,当植株高度低于0.2m时,风速的影响较大。
(3)结合遥感反演的叶面积指数,采用空气动力学粗糙度和叶面积指数及风速的关系,反演了空气动力学粗糙度,反演结果空间分布和误差都反映了实际空气动力学粗糙度的特征,证明空气动力学粗糙度遥感参数化比较成功。
关键词:稀疏植被;空气动力学粗糙度;风速;LAI;植株密度;空气动力学模型Retrieval of Aerodynamic roughness length character over sparse vegetation regionZHANG Jie1,3,HUANG Jianping2,ZHANG Qiang2,31Key Laboratory of Meteorological Disaster(KLMD),Ministry of Education and Jiangsu Province,Nanjing University of Information Science&Technology,Nanjing210044,China2College of atmospheric sciences,Lanzhou University,Lanzhou730000,china3Institute of Arid Meteorology,China Meteorological Administration,Lanzhou730020,ChinaAbstract:Based on observed dada in2005over Dingxi station in semi-arid region of Northwest China,aerodynamic roughness length is estimated,the temporal variable and the relations with wind speed and vegetation density are also bined with LAI from remote sensing,aerodynamic roughness length is simulated by using aerodynamic model. The results show that:(1)Aerodynamic roughness length is on the contrary to wind speed trend.With vegetation density increasing,roughness length will be increased.(2)The effect of vegetation density and LAI on aerodynamic roughness length is large with individual plant height more than0.2m,and wind speed effect on aerodynamic roughness length is large when individual plant height is less than0.2m.(3)The relation and the model of aerodynamic roughness length with LAI,vegetation density and wind speed is put forward by combining with LAI from remote sensing,the model can reflect real status,and equivalent vegetation density is presented by using LAI in the model,which is an available means to parameterize aerodynamic roughness length from remote sensing.Key Words:sparse vegetation;aerodynamic roughness length;wind speed;LAI;vegetation density;aerodynamic model空气动力学粗糙度是从多相流体力学上反映物体表面对流经流体的流型、流态及阻滞力影响的一个综合力学参数。