五年级奥数平面图形

第2讲 平面图形的周长与面积一、知识点周长是指平面图形一周的长度，除了长方形、正方形等特殊图形可以用公式计算其周长外，有时还须仔细观察分析图形，通过添加辅助线，运用平移、分解等方法，将不规则图形转化为规则图形来计算.注 长方形周长=（长+宽）⨯2，正方形周长=边长4⨯，三角形周长=三边之和计算平面图形的面积，除了用长方形、正方形、三角形等面积公式来计算外，有时还须通过找边与边的关系，通过割、补、移、拼、还原等方法来计算.注 长方形面积=长⨯宽，正方形面积=边长⨯边长，三角形面积=底⨯高2÷二、例题精讲例1 如图，在长方形ABCD 中，cm AB 120=，截去一个正方形EBCF 后，则剩下长方形AEFD 的周长等于____________.例2 每个小正方形的周长是12厘米，则它们组合成“十”字图形的周长是_________厘米.例3 如图，10个相同的小长方形拼成一个大长方形，长是9cm ，宽是6cm ，则小长方形的周长等于____________.例4 如图，用四个相同的长方形拼成一个面积为100平方厘米的大正方形，则每个长方形的周长等于___________.例5 如图，正方形ABCD的边长10厘米，长方形EFGH的长为8厘米，宽为5厘米，则阴影部分面积的差是_____________平方厘米.例6 将一个正方形划分为9个小长方形，这些小长方形周长的总和是96厘米，则这个大正方形的面积是多少平方厘米？例7 一个长方形的周长是24厘米，如果长和宽都增加3厘米，则面积增加多少平方厘米？例8 如图，长方形被直线切割成四部分，已知其中三部分的面积分别为28平方厘米，12平方厘米，6平方厘米，则阴影部分的面积是______________平方厘米.三、水平测试1. 如图，5个相同的小长方形拼成一个大正方形.已知大正方形的周长比一个小长方形的周长多10厘米，则小长方形的周长是______________厘米.2. 平行四边形ABCD 的一条边长18，两条高分别为8和10，则平行四边形ABCD 的周长是____________.3. 如图，大正方形边长6厘米，小正方形边长为4厘米，则阴影部分面积为_________平方厘米.4. 如图，10=BC 厘米，6=EC 厘米，直角三角形EDF 的面积比直角三角形FAB 的面积小5平方厘米.则长方形ABCD 的面积是____________平方厘米.5. 一个长方形被分割成8个小长方形，其中有五个小长方形的面积如下图所示（单位：平方分米），则大长方形的面积是___________平方分米.。

3.平面图形的计算2023.11.5 教学目标：1.会理解有关平面图形的长度和周长问题。

2.会运用公式计算，等量代换，添辅助线等方式解题。

3.培养学生自主思考，解题的能力。

感受到数学思维的逻辑性，唯美性。

教学重点：会运用等量代换，添辅助线等方式解题。

教学难点：添辅助线等方式解题。

教学准备：课件教学过程：一、导入1.揭示课题。

（1）我们已经学习了长方形，正方形的图形特征和性质。

初步掌握了长方形和正方形的计算方法。

（2）当增加了三角形，平行四边形和梯形等平面图形之后，平面图形的种类及解题方法也变得更为丰富。

2.这一讲我们专门讨论与图形有关的长度和周长问题。

这些问题常用公式计算，等量代换，添加辅助线等方法加以解决。

二、新授1.例1在一张纸上画出由4个边长为3cm的正方形拼凑或组合成的图形(重叠的线段只算画一次)。

显然，这个图形有多种多样的画法。

下列各图是其中的一部分画法。

（1）在以上这些画法中，哪种画法的周长总长最长？有多长？（2）在所有的这些画法中，哪种画法的周长总长最短？有多长？（1）周长是图形一周线段的长度之和，只要分别求出每个图形的周长就可以了。

图一中重叠的线段最少，线段总长3×4×4=48cm。

（2）图五中重叠的线段最多周长（3+3）×4=24cm。

2.例2右图是一根铁丝围成。

已知两条相邻平行线之间的距离均为1cm，求这根铁丝的长度。

（1）这个图形是不规则的图形，要求出铁丝的总长度必须转化成规则的图形才行。

（2）仔细观察这个图形，发现这个图形的每个角都是直角。

可以将其转化成三个边长为分别3、5、7cm的正方形和一个三边图形。

（3）3×4+5×4+7×4+1×3=63cm。

3.例3如图，四边形BCEF是平行四边形，三角形ABC是一个直角三角形。

BC长8cm，AC长7cm，阴影部分面积比三角形ADH的面积12c㎡，求HC的长度。

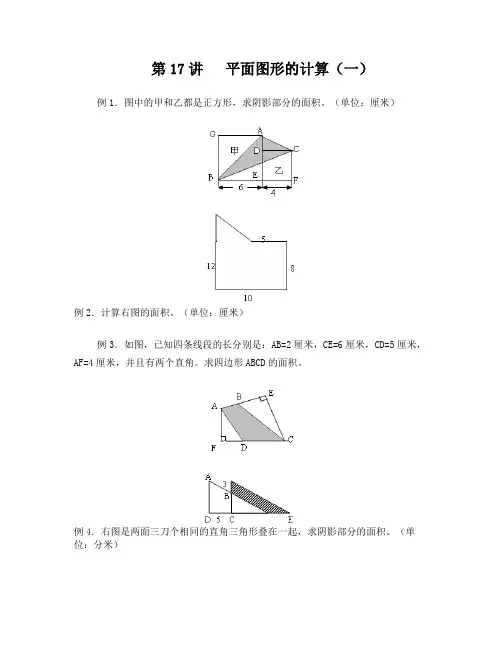
第17讲平面图形的计算（一）例1．图中的甲和乙都是正方形，求阴影部分的面积。

（单位：厘米）例2．计算右图的面积。

（单位：厘米）例3．如图，已知四条线段的长分别是：AB=2厘米，CE=6厘米，CD=5厘米，AF=4厘米，并且有两个直角。

求四边形ABCD的面积。

例4．右图是两面三刀个相同的直角三角形叠在一起，求阴影部分的面积。

（单位：分米）例5．下页左图是一块长方形草地，长方形的长是16，宽是10，中间有两条道路，一条是长方形，一条是平行四边形，那么，有草部分（阴影部分）的面积有多大？（单位：米）练习与思考1．求图中阴影部分的面积。

2．求图中阴影部分的面积。

3．下左图的长方形中，三角形ADE与四边形DEBF和三角形CDF的面积分别相等，求三角形DEF的面积。

4．四中平等四边形ABCD的边BC长10厘米，直角三角形BCE的直角边EC长8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，求CF的长。

5．图中三角形的高为4，面积为16；长方形的宽为6，长方形的面积是三角形面积的多少倍？6．如图，长方形的长是8，宽是6，A和B是宽的中点，求长方形内阴影部分的面积。

7．如图，BC长为5，求画斜线的两个三角形的面积之和。

8．上右图是两个一样的直角三角形重叠在一起，按照图上标出的数，计算阴影部分的面积。

9．右图是一块长方形草地，长方形长为16，宽为12，中间有一条宽为2的道路，求草地（阴影部分）的面积。

简便计算作业（12月23日）：1.996+19.97+199.82.894.68+4.686.11+4.68 754.7+15.925平均数问题作业（12月23日）：1.已知九个数的平均数是72.去掉一个数之后，余下的数的平均数是78。

去掉的数是多少？2.甲、乙、丙三个小组的同学去植树，甲、乙两组平均每组植树18棵，甲、丙两组平均每组植树17棵，乙、丙两组平均每组植树19棵。

三个小组各植树多少棵？3.五一班同学数学考试平均成绩91.5分，事后复查发现计算成绩时将一位同学的98分误作89分计算了。

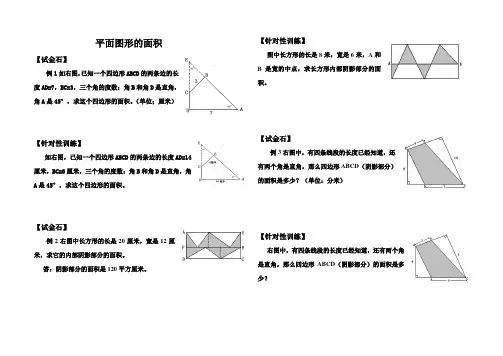
平面图形的面积【试金石】例1如右图，已知一个四边形ABCD的两条边的长度AD=7，BC=3，三个角的度数：角B和角D是直角，角A是45°，求这个四边形的面积。

（单位；厘米）【针对性训练】如右图，已知一个四边形ABCD的两条边的长度AD=14厘米，BC=6厘米，三个角的度数：角B和角D是直角，角A是45°，求这个四边形的面积。

【试金石】例2右图中长方形的长是20厘米，宽是12厘米，求它的内部阴影部分的面积。

答：阴影部分的面积是120平方厘米。

【针对性训练】图中长方形的长是8米，宽是6米，A和B是宽的中点，求长方形内部阴影部分的面积。

【试金石】例3右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？（单位：分米）【针对性训练】右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？【试金石】例4如右图，甲、乙两图形都是正方形，它们的边长分别是10厘米和12厘米，求阴影部分的面积。

【针对性训练】如右图，甲、乙两图形都是正方形，它们的边长分别是6厘米和8厘米，求阴影部分的面积。

【试金石】例5【针对性训练】【试金石】【针对性训练】【智能提速训练营】1、如图，已知BD长是2厘米，DC长是3厘米，E是AD的中点，如果三角形ABD的面积是5平方厘米，那么三角形DEC的面积是多少？2、如图，已知平行四边形ABCD的面积是60平方分米，E、F分别是AB、AD边上的中点，图中阴影部分的面积是多少平方分米？3、如图，在平行四边形ABCD中，AE=ED，BF=FC，CG=GD，平行四边形ABCD的面积是阴影三角形EFG的多少倍？4、如图，BD=6厘米，BC=15厘米，△ABD的面积是24平方厘米，△ADC 的面积是多少平方厘米？5、右图中，有四条线段的长度已经知道，还有两个角是直角，那么四边形ABCD（阴影部分）的面积是多少？（单位：厘米）6、如图，梯形的面积是70平方厘米，上底8厘米，下底12厘米，阴影部分的面积是多少平方厘米？7、如图，四边形ABCD是平行四边形，DC=CE，如果△BCE的面积是15平方厘米，那么梯形ABED的面积是多少平方厘米？8、如图，平行四边形的面积是60平方厘米，阴影三角形的面积是多少平方厘米？9、如图，正方形ABCD的边长是4厘米，CG=3厘米，长方形DEFG的长DG=5厘米，那么它的宽DE是多少厘米？10、如图，四边形ABCD内有一点O，O点到四条边的垂线长都是4厘米，已知四边形的周长是36厘米，四边形ABCD的面积是多少平方厘米？11、如图，已知ABFE是平行四边形，ABCD是长方形，且AD=6厘米，AB=3厘米，CO=2厘米，阴影部分的面积是多少平方厘米？12、一个长方形被两条直线分成四个长方形，其中三个的面积分别是20平方米、25平方米和30平方米，阴影部分的面积是多少平方米？13、如右图，已知正方形ABCD和正方形CEFG，且正方形ABCD每边长为10厘米，求图中阴影（三角形BFD）部分的面积。

完整版)五年级奥数平面图形面积计算五年级奥数第六讲——平面图形面积的计算一、知识要点1.基本平面图形特征及面积公式正方形：特征：四条边相等，四个角都是直角，有四条对称轴。

面积公式：S=边长的平方长方形：特征：对边相等，四个角都是直角，有二条对称轴。

面积公式：S=长×宽平行四边形：特征：两组对边平行且相等，对角相等，相邻的两个角之和为180°，容易变形。

面积公式：S=底边×高三角形：特征：两边之和大于第三条边，两边之差小于第三条边，三个角的内角和是180°，具有稳定性。

面积公式：S=底边×XXX÷2梯形：特征：只有一组对边平行，中位线等于上下底和的一半。

面积公式：S=(上底+下底)×高÷22.基本解题方法：由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先根据图形的基本关系，再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图形分别计算。

典型例题】例1】已知平行四边形的面积是28平方厘米，求阴影部分的面积。

例2】求图中阴影部分的面积。

例3】如图所示，甲三角形的面积比乙三角形的面积大6平方厘米，求CE的长度。

例4】两条对角线把梯形ABCD分割成四个三角形。

已知两个三角形的面积（如图所示），求另两个三角形的面积各是多少？练与拓展】1.计算下面图形的面积。

2.下面的梯形中，阴影部分面积是150平方厘米，求梯形的面积。

3.正方形ABCD的边长是12厘米，已知DE是EC长度的2倍，求三角形DEF的面积和CF的长。

4.平行四边形ABCD的边长BC=10厘米，直角三角形BCE的直角边EC长8厘米，已知阴影部分的面积比三角形EFG的面积大10平方厘米，求CF的长。

5.正方形ABCD的面积是100平方厘米，AE=8厘米，请计算以下图形的面积。

1.在一块长80米、宽30米的长方形地上，修了宽为2米和3米的两条小路，求草地的面积。

平面图形1、 和差法：分割、合并、倍数比2、 运动法：3、 等积变换法：等底、等高则等积；等积、等高则等底；等积、等底则等高。

例1、求阴影部分的面积。

例2、大、小两个正方形的边长分别是8厘米和6厘米， 求阴影部分的面积。

例3、两个相同的直角三角形如图重叠在一起， 求阴影部分的面积。

例4、求阴影部分面积。

例5、图中长方形ABCD 中AB=5厘米，BC=8厘米。

三角形DEF （甲）的面积 比三角形ABF （乙）的面积大8平方厘米。

求DE 的长。

3cm4cm6cm5cm2cm12cm甲ABCDEF乙AD B C 10cm 10cm24cm45° E5cm例6、在三角形ABC 中，DC=2BD ，CE=3AE ，三角形ADE 的面积是 8平方厘米。

求三角形ABC 的面积。

例7、四边形ABCD 中，AC 和BD 互相垂直，AC=20厘米，BD=15厘米。

求四边形的面积。

例8、在四边形ABCD 中，∠C=45°，∠B=90°，∠D=90°， AD=4cm ，BC=12cm 。

求四边形ABCD 的面积。

例9、AF=2cm,AB=4cm,CD=5cm,DE=8cm,∠B=∠E=90°。

求四边形ACDF 的面积。

例10、已知大正方形比小正方形边长多2厘米，大正方形比小正方形的面积大10平方厘米。

求大、小正方形的面积各数多少平方厘米。

ABCDC45°AB CDABCDEF 4cm8cm2cm练习1、图中两个正方形的边长是10厘米和7厘米，求阴影部分的面积（如图）练习2、如下图，在三角形ABC中，AD=BD,CE=3BE。

若三角形BED的面积是1平方厘米，则三角形ABC的面积是多少平方厘米？练习3、三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B长40厘米, BC长多少厘米.练习4、在右图中(单位:厘米),两个阴影部分面积的和是平方厘米.练习5、ABC是等腰直角三角形. D是半圆周的中点,BC是半圆的直径,已知:AB=BC=10,那么阴影部分的面积是多少?练习6、已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积. C②①A B121520A10DCB练习7、右图中三角形是等腰直角三角形, 阴影部分的面积是 (平方厘米).练习8、如右图,阴影部分的面积是 .练习9、如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π练习10、ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?练习11、在四边形ABCD 中，∠C=135°，∠D=90°。

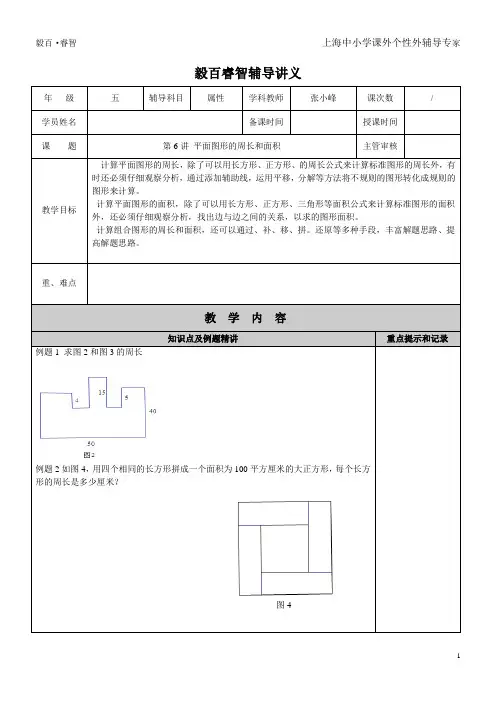
毅百睿智辅导讲义年级五辅导科目属性学科教师张小峰课次数/学员姓名备课时间授课时间课题第6讲平面图形的周长和面积主管审核教学目标计算平面图形的周长，除了可以用长方形、正方形、的周长公式来计算标准图形的周长外，有时还必须仔细观察分析，通过添加辅助线，运用平移，分解等方法将不规则的图形转化成规则的图形来计算。

计算平面图形的面积，除了可以用长方形、正方形、三角形等面积公式来计算标准图形的面积外，还必须仔细观察分析，找出边与边之间的关系，以求的图形面积。

计算组合图形的周长和面积，还可以通过、补、移、拼。

还原等多种手段，丰富解题思路、提高解题思路。

重、难点教学内容知识点及例题精讲重点提示和记录例题1 求图2和图3的周长例题2如图4，用四个相同的长方形拼成一个面积为100平方厘米的大正方形，每个长方形的周长是多少厘米？图4例题3.将一个正方形划分为9个小长方形，这些小长方形的周长的总和是96厘米，那么大正方形的面积是多少？例题4.如图6，在长方形ABCD中,AB=120厘米，截去一个正方形EBCF后，问还剩下长方形AEFD的周长是多少厘米？例题5.如图7，正方形ABCD的面积为10厘米，长方形EFHG的长为8厘米，宽为5厘米，问阴影部分甲与阴影部分乙的面积之差为多少平方厘米？图6甲乙图7例题6 如图8，在正方形ABCD中，红色、绿色正方形的面积分别为52和13，且红、绿两个正方形有一个顶点重合，黄色正方形的一个顶点是红色正方形两条对角线的交点，另一顶点是绿色正方形两条对角线的交点，求黄色正方形的面积。

例题7 如图10，红、黄、绿三块大小相同的面积的正方形纸片，放在一个底为正方形的盒子内，它们相互重叠，在露出的部分中，红色面积20，黄色面积是14，绿色面积是10，求正方形的面积。

黄颜色的长边=绿颜色的长边=红颜色的边长红颜色的边长+绿颜色短边=正方形边长红颜色的边长+黄颜色短边=正方形边长所以，绿颜色短边=黄颜色短边，所以把上图进行切割，即如下图所示，并且将剩余黄色进行平移构成一个由两个相同的长方形和两个大小不同的正方形组成的图形。

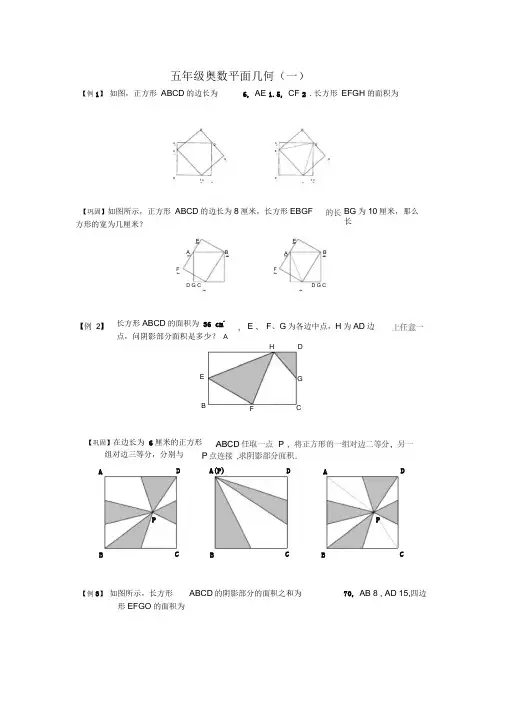
五年级奥数平面几何（一）【例1】 如图，正方形 ABCD 的边长为 6, AE 1.5, CF 2 .长方形 EFGH 的面积为GGBBA BBFFE HDEGB CF D A(P) DDA AP PA E A EBG 为10厘米，那么长【巩固】如图所示，正方形 ABCD 的边长为8厘米，长方形EBGF 方形的宽为几厘米？ 长方形ABCD 的面积为 36 cm 2点，问阴影部分面积是多少？ AF 、G 为各边中点，H 为AD 边F C F CD G CD G C【巩固】在边长为 6厘米的正方形 组对边三等分，分别与 C CCB B B【例3】 如图所示，长方形 形EFGO 的面积为ABCD 的阴影部分的面积之和为 70, AB 8 , AD 15,四边【巩固】【例4】【例5】【例6】如图，长方形ABCD的面积是36,的面积为E是AD的三等分点，AE 2ED ,则阴影部分已知ABC为等边三角形，面积为143,求阴影五边形的面积.乙、丙面积和为如图，已知CD左边部分面积是400 , D、E、F分别为三边的中点，已知甲、（丙是三角形HBC）5 , DE 7 , EF38,右边部分面积是15,65,FG 6,线段AB将图形分成两部分, 那么三角形ADG的面积是如图在△ ABC中，D,E分另U是AB,AC上的点，且AD: AB 2:5 , AE: AC 4:7 ,S A ADE 16平方厘米，求△ ABC的面积.【巩固】如图，三角形 ABC 中，AB 是AD 的5倍，AC 是AE 的3倍，如果三角形 ADE 的 面积等于1,那么三角形 ABC 的面积是多少？【巩固】如图，三角形ABC 被分成了甲（阴影部分）、乙两部分，BD DC 4 , BE 3 , AE 6, 乙部分面积是甲部分面积的几倍？行四边形ABCD 的面积是2 , 求平行四边形 ABCD 与四边形EFGH 的面积比.AAB C【例7】 如图在△ ABC 中，D 在BA 的延长线上,AE:EC 3:2 , S A ADE 12 平方厘米，求E 在AC 上，且 △ ABC 的面积.AB: AD 5:2,【例8】如图，平行四边形 ABCD, BE AB , CF2CB , GD 3DC , HA 4AD ,平如图所示， ABC 中，ABC 90 , AB 3 , BC 5,以AC 为一边向 ABC 外 作正方形ACDE ，中心为O,求 OBC 的面积.如图，以正方形的边 AB 为斜边在正方形作直角三角形ABE, AEB 90 , AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ，求三角形 OBE 的面积.【例9】如图所示的四边形的面积等于多少?【例10】【例11】 【例12】AB ED , AF CD , BC EF ，且有 AB 平行如下图，六边形 ABCDEF 中，于ED , AF 平行于CD , BC 平行于EF ,对角线FD 垂直于BD ,已知FD 24厘 米，BD 18厘米，请问六边形 ABCDEF 的面积是多少平方厘米?E E【例13】如图，三角形ABC 的面积是1 , E 是AC 的中点，点D 在BC 上，且BD :DC 1:2, AD 与BE 交于点F .则四边形 DFEC 的面积等于 .【例14】四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形 ABD 的面积等于三角形 BCD 的面积的1 ,且AO 2 , DO 3 ,那么CO 的长度是DO 的长3【巩固】如图，四边形被两条对角线分成 4个三角形，其中三个三角形的面积已知,求：⑴三角形 BGC 的面积；(2) AG:GC ?【例15】 如图，平行四边形 ABCD 的对角线交于 O 点，△ CEF 、△ OEF 、△ ODF 、△ BOE的面积依次是 2、4、4和6.求：⑴求 △ OCF 的面积；⑵求 △ GCE 的面积.【巩固】如图，长方形 ABCD 的面积是 分的面积是多少平方厘米 ？2平方厘米，EC 2DE , F 是DG 的中点.阴影部D EC【例16】如图，长方形ABCD中，BE:EC 2:3 , DF :FC 1:2 ,三角形DFG的面积为2平方厘米，求长方形ABCD【例17】如图，正方形ABCD面积为3平方厘米，M是AD边上的中点.求图中阴影部分的面积.【巩固】在下图的正方形ABCD中，E是BC边的中点，AE与BD相交于F点，三角形BEF 的面积为1平方厘米，那么正方形ABCD面积是平方厘米.【例18】已知ABCD是平行四边形，BC: CE 3:2，三角形ODE的面积为6平方厘米.则阴影部分的面积是平方厘米.【巩固】右图中 ABCD 是梯形，ABED 是平行四边形，已知三角形面积如图所示 （单位：平方厘米），阴影部分的面积是 平方厘米.【巩固】右图中 ABCD 是梯形，ABED 是平行四边形，已知三角形面积如图所示 （单位：平方厘米），阴影部分的面积是 平方厘米.知正方形DEFG 的面积48 , AK:KB 1:3，贝U BKD 的面积是多少?【例21】 下图中，四边形ABCD 都是边长为1的正方形，E 、F 、G 、H 分别是AB , BC ,【例19】如图，长方形 ABCD 被CE 、平方厘米，那么余下的四边形DF 分成四块，已知其中 3块的面积分别为 2、5、8 OFBC 的面积为 __________ 垩方厘米.【例20】如图，ABC 是等腰直角三角形,DEFG 是正方形，线段AB 与CD 相交于K 点.已CD, DA 的中点，如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m，那么，（m n ）的值等于 n则，△ ADE : §9边形DEGF【巩固】如图， DE 平行BC ，且AD 2 , AB 5 , AE 4，求AC 的长.△ ABC 中，DE , FG , MN , PQ , BC 互相平行,DF FM MP PB,贝U:岛边形DEGF : S 四边形FGNM : S 四边形MNQP : S 四边形PQCB【例22】如图，△ ABC 中,DE , FG , BC 互相平行,AD DF FB ,【巩固】如图，AD §△ ADE:&9边形FGCB【例23】如图，已知正方形 ABCD 的边长为4 , F 是BC 边的中点，E 是DC 边上的点,且DE :EC 1:3 , AF 与BE 相交于点G ,求S【例24】如图所示，已知平行四边形 ABCD 的面积是1 , E 、F 是AB 、AD 的中点，BF 交EC于M,求 BMG 的面积.△ABG。

同学个性化教学设计年级：教师: 科目：
班主任：日期: 时段:
【例 1】 在梯形中阴影部分面积是150平方厘米，求梯形面积。

【巩固】如图，已知平行四边形面积是48平方厘米，求阴影部分面积。

【例 2】 如图，是两个完全相同的直角三角形叠在一起，求阴影部分的面积。

（单位：分米）
【例 3】 如图，将长为9厘米、宽为6厘米的长方形划分成四个三角形，其面积分别为1S 、2S 、3S 、
4S ，且4321S S S S +==,求4S 。

【巩固】如图，四年级ABCD是直角三角形，其中AD=12厘米，AB=8厘米，BC=15厘米，且△ADE 四边形DEBF及△CDF的面积相等，求三角形EBF的面积。

【例 4】如图，AE=5厘米，CF=2厘米，AB=6厘米，CD=4厘米，∠B=∠D=90°。

求四边形AFCE 的面积。

【巩固】如图，四边形ABCD中，AE=5厘米，AB=10厘米，FC=12厘米，∠B=∠D=90°，求四边形AFCE的面积。

【例 5】如图，求图示长方形中阴影部分的面积。

（单位：厘米）
【例 6】如图，平行四边形ABCD的边长BC=10厘米，直角三角形BCE的直角边CE长8厘米。

已知阴影部分的面积比三角形FEG的面积大10平方厘米。

求CF的长。

【巩固】如图，正方形ABCD的边长是12厘米，已知DE是EC的长度的2倍。

求（1）△DEF的面积；(2)CF的长。

学生签字：__________
教研组长签字：____
_______。

奥数教课设计《平面图形的周长和面积》教课对象：已学完义务教育小学五年级的学生。

教课目的：（1）利用长方形、正方形的周长公式，来计算规则图形的周长。

除此，经过增添协助线，运用平移、分解等方法，将不规则图形转变成规则图形来计算。

b5E2RGbCAP（2）除利用长方形、正方形、三角形、平行四边形、梯形等面积公式，来计算规则图形的面积外，还一定认真剖析察看，找出边与边的关系，进而使问题化难为易，以求得图形的面积。

p1EanqFDPw教课准备：三角板一付、底稿一本。

课时安排： 2 课时教课过程：第一课时一、明确学习目标、复习公式。

（1）课件向学生展现本节课要达到的目标。

（2）复习已学平面图形的周长、面积公式。

学生回想长方形、正方形、三角形、平行四边形、梯形的周长、面积公式，教师课件展现。

二、学习例题。

1、电脑出示例 1：例 1：在长方形 ABCD 中，AB=120 厘米，截去一个正方形 EBCF 后，剩下长方形 AEFD 的周长是多少？（如右图） DXDiTa9E3d剖析：依据已知条件，察看图形可得：EBCF 是正方形，则EB=EF，AE+EB=AB ，获得AE+EF=AB RTCrpUDGiT解： 120×2=240（厘米）2、回首整理解题思路：利用长方形和正方形图形的特点和周长的计算公式，解决问题。

3、电脑出示例 2：例2：四个同样的长方形和一个正方形，拼成一个大正方形和一个小正方形，大、小正方形的面积分别为 64 平方厘米和 9 平方厘米，求长方形的面积。

5PCzVD7HxA剖析：由图和题义可知下边信息：小正方形的边长+长方形的宽=长方形的长；a2大=64，则a 大 =8；a2小=9，则 a 小 =3，假定长方形的长和宽分别为x，y。

解： y=(8-3)÷ 2=2.5，x =8- 2.5 =5.5S= 5.5×2.5=13.75 （平方厘米）4、小结提升：谈谈解答这种题要注意哪些问题？（注：本课对例题的教课主要采纳上边的流程：出示例题——学生试试解答——教师有针对性进行解说——总结方法，贯通融会） jLBHrnAILg三、稳固练习。

1、知识要点 1. 2. 五年级奥数第六讲平面图形面积的计算特征 面积公式正方形① 四条边都相等。

② 四个角都是直角。

③ 有四条对称轴。

S=aa长方形① 对边相等。

② 四个角都是直角。

③ 有二条对称轴。

S=ab平行四边形① 两组对边平行且相等。

② 对角相等，相邻的两个角之和为 180° ③ 平行四边形容易变形。

S=ah三角形① 两边之和大于第三条边。

② 两边之差小于第三条边。

③ 三个角的内角和是 180°。

④ 有三条边和三个角，具有稳定性。

S=ah * 2梯形① 只有一组对边平行。

② 中位线等于上下底和的一半。

S=(a+b)h - 2基本平面图形特征及面积公式 基本解题方法:由两个或多个简单的基本几何图形组合成的组合图形，要计算这样的组合图形面积，先根 据图形的基本关系，再运用分解、组合、平移、割补、添辅助线等几种方法将图形变成基本图 形分别计算。

【典型例题】28平方厘米,----- 5 IP ---------/ [ / *f【例1】已知平行四边表的面积是求阴影部分的面积。

【练一练】如果用铁丝围成如下图一样的 平行四边形，需要用多少厘米铁丝？ （单位：厘米）2【练一练】下图中甲和乙都是正方形，求阴影部分 的面积。

（单位：厘米）【例3】如图所示，甲三角形的面积比【练一练】平行四边形 ABCD 的边长BC=10厘米，直角三角形 BCE 的直角 边EC 长8厘米，已知阴影部分的面积比 三角形EFG 的面积大10平方厘米。

求CF 的长。

【例4】两条对角线把梯形 ABCD 分割成四个三角形。

已知两个三角形的面积（如图所示） ，求另两个三角形 的面积各是多少？（单位：厘米）【练一练】下面的梯形 ABCD 中，下底是 上底的2倍，E 是AB 的中点，求梯形 ABCD 的面积是三角形EDB 面积的多少倍？【练一练】一个长方形的草 坪，中间有两个人 行道。

高是14 求草坪的面积。