地球物理反演理论.pdf

目录摘要 (2)一、反演问题基本概念 (2)二、线性反演问题 (3)三、线性反演问题的求解 (5)3。

1适定和超定问题 (5)3。

2欠定问题 (5)3.3混定问题 (6)四、非线性反演方法 (6)4。

1线性化迭代算法 (6)4。

2最速下降法 (6)4.3 共轭梯度法 (7)4。

4遗传算法 (8)4。

5模拟退货法 (9)4。

6人工神经网络法 (9)总结: (10)地球物理反演理论综述摘要在地球物理学中,其核心问题就是如何根据地面上的观测信号推测地球内部与信号有关部分的物理状态。

不同的地球物理问题，其数学物理是不同的；同一个物理问题，应为观测方式不同,也会有不同的物理模型。

在地球物理学中,大多数的观测数据核模型参数之间是不满足线性关系的.但是在一定近似条件想均可简化或近似简化为线性关系.因此线性反演是地球物理的关键问题。

关键词: 反演；线性反演；非线性反演一、反演问题基本概念把数据模型中的一个点定义为m，把数据空间中的一个点定义为d，两者的关系可以成：d=Gm式中，G为模型空间M到数据空间D的一个映射，也称反函数算子，反应了模型m与数据d之间的物理规律从空间映射来看，如果存在一个映射A，使得m=Ad则A为有数据空间D到模型空间M的映射，即A为G的逆映射，称逆算子。

也可以写成=dm1-G我们把给定模型m求解数据d的过程称为正演;把给定数据d求解模型参数m的过程称为繁衍问题.图1。

1模型空间域数据空间之间的映射关系示意图反演问题的研究归纳为四个方面的问题：1) 解的存在性：给定数据d ，按照物理定律，能否找到满足要求的模型参数m ；2) 模型构制：若解存在,如何让构制问题的数学模型使得反演问题的解能迅速而准确地确定；3) 解的非唯一性：若解存在，其是否唯一;4) 解的评价：若解的非唯一性的，如何从非唯一解中获取真实解的信息.关于上述四方面问题的研究就构成了地球物理反演的基本理论。

二、线性反演问题为了使问题简单明了而又不失一般性，我们在此讨论一维问题。

地球物理反演理论一、解释下列概念1.分辨矩阵数据分辨矩阵描述了使用估计的模型参数得到的数据预测值与数据观测值的拟合程度，可以表示为[][]pre est g obs g obs obs d Gm G G d GG d Nd --====，其中，方阵g N GG -=称为数据分辨矩阵。

它不是数据的函数, 而仅仅是数据核G （它体现了模型及实验的几何特征）以及对问题所施加的任何先验信息的函数。

模型分辨矩阵是数据核和对问题所附加的先验信息的函数，与数据的真实值无关，可以表示为()()est g obs g true g ture ture m G d G Gm G G m Rm ---====，其中R 称为模型分辨矩阵。

2.协方差模型参数的协方差取决于数据的协方差以及由数据误差映射成模型参数误差的方式。

其映射只是数据核和其广义逆的函数, 而与数据本身无关。

在地球物理反演问题中,许多问题属于混定形式。

在这种情况下,既要保证模型参数的高分辨率, 又要得到很小的模型协方差是不可能的,两者不可兼得,只 有采取折衷的办法。

可以通过选择一个使分辨率展布与方差大小加权之和取极小的广义逆来研究这一问题:()(1)(cov )u aspread R size m α+-如果令加权参数α接近1,那么广义逆的模型分辨矩阵将具有很小的展布,但是模型参数将具有很大的方差。

而如果令α接近0,那么模型参数将具有相对较小的方差, 但是其分辨率将具有很大的展布。

3.适定与不适定问题适定问题是指满足下列三个要求的问题：①解是存在的；②解是惟一的；③解连续依赖于定解条件。

这三个要求中，只要有一个不满足，则称之为不适定问题4.正则化用一组与原不适定问题相“邻近”的适定问题的解去逼近原问题的解,这种方法称为正则化方法。

对于方程c Gm d =，若其是不稳定的，则可以表述为()T T c G G I m G d α+=，其中α称为正则参数，其正则解为1()T T c m G G I G d α-=+。

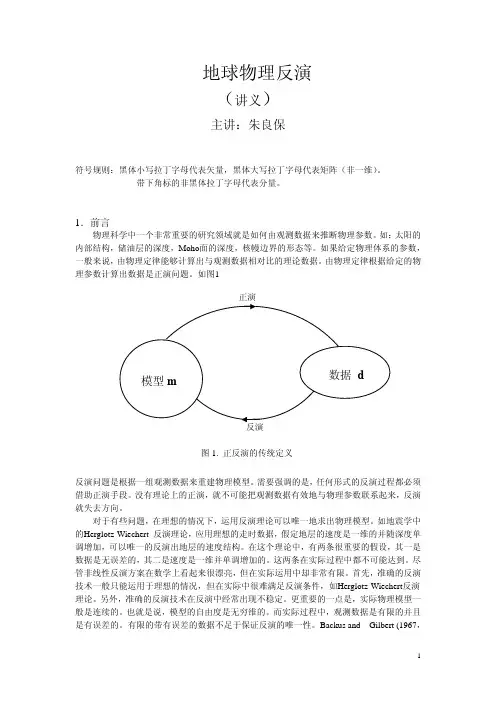
地球物理学中的反演问题1、介绍物理科学的一个重要的方面是根据数据对物理参数做出推断。

通常，物理定律提供了计算给定模型的数据值的方法，这就被称为“正演问题”，见图-1。

在反演问题中，我们的目标是根据一组测量值重建物理模型。

在理想情况下，存在一个确定的理论规定了这些数据应该怎样转换从而重现该模型。

从选择的一些例子来看，这样一个存在的理论假定了（我们）所需要的无限的、无噪声的数据是可以获得的。

在一个空间维度中，当所有能量的反射系数已知时，量子力学势能可以被重建[Marchenko,1955; Brurridge,1980]。

这种手法可以推广到三维空间[Newton,1989]，但是在那样的情形下要求有多余数据组，其中的原因并不是很理解。

在一条一维的线上的质量密度可以通过对它的所有本征频率的测量来构建[Borg,1946]，但是因为这个问题的对称性，因而只有偶数部分的质量密度可以被确定。

如果（地下的）地震波速只和深度有关，那么根据地震波的距离，运用阿贝尔变换，这个速度可以通过测定震波的抵达时间来精确构建[Herglotz,1907;Wiechert,1907]。

从数学上看，这个问题和构建三维空间中的球对称量子力学势是相同的[Keller et al.,1956]。

然而，当波速随着深度单调增加时，Herglotz-Wiechert的构建法只能给出唯一解[Gerver and Markushevitch,1966]。

这种情况和量子力学是相似的，在量子力学中，当电势没有局部最小值时，径向对称势只能被唯一建立[Sabatier,1973]。

（量子力学相关概念不熟悉，翻译起来有点坑~~）图-1尽管精确非线性反演法在数学表达上是美妙的，但它们的适用性是有限的。

原因有很多。

第一，精确的反演法通常只在理想状态下适用，这在实际中可能无法保持。

比如，Herglotz-Wiechert反演假定了地下的波速只依赖于深度并且随着深度单调增加。