当前位置：文档之家 › 有心力的基本性质

有心力的基本性质

  • 格式：ppt
  • 大小：484.50 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

《理论力学》试题库(1)

《理论力学》试题库(1)

《理论力学》试题库一、判断体：1.没有参照系就无法描述物体的位置和运动。

2.经典力学可分为牛顿力学和分析力学两大部分。

3.运动是绝对的，而运动的描述是相对的。

4.相对一个惯性系运动的参照系一定不是惯性系。

5.相对一个惯性系作匀速直线运动的参照系也是一个惯性系。

6.经典力学的相对性原理表明：所有参照系等价。

7.通过力学实验不能确定参照系是否为惯性系。

8.通过力学实验不能确定参照系是否在运动。

9.位移矢量描述质点的位置。

10.表述为时间函数的位置变量称为运动学方程。

11.质点的轨道方程可以由运动学方程消去时间变量得到。

12.速度矢量的变化率定义为加速度。

13.速率对时间的一阶导数定义为加速度。

14.速率对时间的一阶导数等于切向加速度。

15.若质点的加速度为常矢量则其必作直线运动。

16.极坐标系中的径向加速度就是向心加速度。

17.在对物体运动的描述中，参照系和坐标系是等价的。

18.若质点作圆周运动，则其加速度恒指向圆心。

19.牛顿第二定律只适用于惯性系。

20.若质点组不受外力则机械能守恒。

21.质点组内力对任意点力矩的矢量和与内力有关。

22.内力不能改变系统的机械能。

23.内力可以改变系统的机械能。

24.内力不改变系统的动量。

25.内力可以改变系统的动量。

26.质点组内力的总功可以不等于零。

27.质点系动量守恒时动量矩不一定守恒。

28.质点系内力对任意点力矩的矢量和必为零。

29.质点系的质心位置与质点系各质点的质量和位置有关。

30.质点的动量守恒时对任意定点的动量矩也守恒。

31.质点系的动量守恒时对任意定点的动量矩也守恒。

32.质点系对某点的动量矩守恒则其动量必定守恒。

33.刚体是一种理想模型。

34.刚体的内力做的总功为零。

35.刚体平衡的充要条件是所受外力的矢量和为零。

36.刚体处于平衡状态的充要条件是所受外力的主矢和主矩均为零。

37.正交轴定理适用于任何形式的刚体。

38.正交轴定理只适用于平面薄板形的刚体。

民院理论力学复习考试点

民院理论力学复习考试点

理论力学复习
一、题型
1、判断题（10分）
2、填空题（20分）
3、简答题（10分）
涉及第四章---“地球上的所有物体是否都受科里奥利里力”
4、证明题（20分）
本人建议：重点看一下老师最后布置的4道题，尤其是根据最小作用量原理（哈密顿原理）证明拉格朗日方程、泊松括号的性质。

5、计算题（40分）
有三个大题：第一章有一题，第五章有2题（用虚功原理求静平衡；拉式方程L的应用）友情提醒：第三章不考大题
二、各章的复习知识点
第一章：主要是基本概念、定义。

1、三种坐标系的描述（直角、极、自然坐标系）:关于v,a的表示。

2、非惯性系动力学、功、能、惯性力的定义，有心力的基本性质（比耐公式、开普勒定律）
3、三大定理（动能、动量、角动量）及三大定律。

第二章：主要弄清楚{质心运动定理、柯尼希定理、变质量物体的运动及内力对物体的影
响（在动能、动量、角动量定理中，注意区别，内力对动能的作用不可省略）}。

第三章：主要知道{描述刚体位置的独立变量、力系的简化及刚体平衡}
第四章：科里奥利力
第五章：基本都要掌握。

1.概念：约束、实位移与虚位移、循环积分与能量积分、哈密顿原理的物理思想
2、两大原理：虚功原理与哈密顿原理
3、拉式方程与正则方程，泊松括号
友情提示：老师传的分析力学的资料第54页，重点看一下哈！
祝：
考试取得好成绩哦！！！。

理论力学(4)有心力

理论力学(4)有心力
2
动量矩（角动量）守恒
J r p m r v mrvq mr 2q
2017/3/15 有心力 4
有心力的基本方程
m r rq 2 Fr F r 2 r q h


(1.9.6)
有心力是保守力
证明： W A F d r A Fr dr Fq rdq


上式代替(1.9.6)中的一式，得基本方程
1 m r 2 r 2q 2 V r E 2 r 2q h


2017/3/15
有心力
6
（2）轨道微分方程——比耐公式 求轨道方程的一般方法：求出运动规律，在运动 方程中消去时间t。 有心力的情况，可以先从运动微分方程中消去 dt，得轨道微分方程。 令 u 1/ r
第二宇宙速度
2017/3/15
有心力
20
第三宇宙速度:逃出太阳系的速度 在地球绕太阳运行的轨道上发射物体可以脱离 太阳系的速度
2GM ' v , M ' 太阳质量, r ' 地球轨道半径 r' 2GM ' 42km / s 计算得 v r'
考虑地球公转速度约30千米/秒,只需12千米/秒的 速度. 地球上的发射速度为v3,则
2 k 代入(1.9.28)后,得 E m 2a
2017/3/15 有心力 18
宇宙速度 椭圆轨道
1 2 k 2m k 2m mv 2 r 2a
(1.9.32)
第一宇宙速度(环绕速度) 对绕地球运行的卫星而言,可令
a r 地球半径, k 2 GM 地 gr 2
2 2 1 gr m gr m 2 mv1 , 2 r 2r

§9 有心力

§9 有心力

2 2 1 h2 dr h k 2m 2 m 4 常数E r 2 2 r d r r
h2 dr 2 h2 2k 2 1 2 4 2m E r d r r
dr r 2 2 E 2k 2 h2 2 d h m r r
代入 u A cos B sin
k' mh2
1 y
A cos B sin sin
k' mh2 A(1 cos ) B sin A(1 cos ) B sin sin
无穷远处，1 A(1 cos ) B B

sin
h2 k 2 r 1 ( Ah2 k 2 ) cos
u A cos 0 k h2
2
化简 通解
d 2u k2 u 2 2 d h
极坐标下标准圆锥曲线的表达式为 e<1 椭圆
p r 1 e cos
2 2
e=1 抛物线 e>1 双曲线
h k r 2 2 1 ( Ah k ) cos
四、应用
（一）平方反比引力---行星的运动
平方反比引力：
F GM m m k 2 2 mk 2 u2 r2 r
1、用比耐公式讨论
考虑r 1 u
d 2u mk 2 u 2 hu u k 2 u2 d 2 m
2 2
取恰当 极轴使 0 0
守恒方程 (动量矩值守恒+ 机械能守恒)
r与θ之间的微 分关系?
应该从运动微分方程-基本方程出发进行推导.
2 F (r ) m r r 基本方程 2 rh
令 u

§1.8 有心力

§1.8 有心力

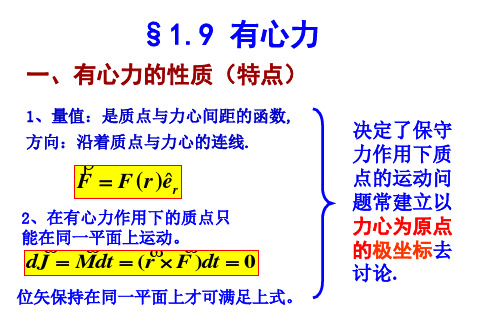
§1、8有心力1、有心力的基本性质（有心运动的特点）有心力 质点所受力的作用线始终通过定点，定点为力心；有心运动 质点在有心力作用下的运动⇒有心运动 这时)(r F F =方向沿质点与力心联线， 又分引力，斥力；有心运动在物理学中占有极其重要的地位；有心运动求解方法：运动微分方程；三个基本定理。

（1）有心运动⇒动量矩守恒⇒质点作平面曲线运动选力心为原点 0=M c J=∴ 质点作平面曲线运动 运动平面垂直于J选用极坐标系 θθv r m v m v m r P r J r⨯=+⨯=⨯=)( mh mr mrv J ===θθ 2θ 2r h =⇒ （1） h 由初始条件确定（2）有心力为保守力，质点作有心运动时机械能守恒在极坐标系下，00)(r F r r F F r== 00θθ rd r dr r d +=则)()(12V V Vdr dr r F rd F dr F r d F W BABABABAr --=∇-==+=⋅=⎰⎰⎰⎰θθ这时 E V T =+ E r V r rm =++)()(21222θ （2） ⎪⎩⎪⎨⎧=++=⇒E r V r rm h r )()(212222θθ 两个运动积分（关于θ,r 的一阶微分方程组）2、轨道微分方程⎪⎩⎪⎨⎧=++=)2()()(21)1(2222E r V r rm h r θθ 由（1）⇒)(r θ ，代入（2）)()(t r r r r=⇒⇒ 代入（1）)()()()(θθθθθr r t t r r t =⇒⎩⎨⎧==⇒=⇒运动方程 轨道方程亦可由)(),(r r rθ 消去时间t 得22222)(2rmh r V E rmhd dr --±=θ⇒积分)(θr r =⇒现导出比耐（Binet ）公式0=θF )()(2r F r r m =-∴θ取 ru 1= 则2hu =θ又 θθθθθd du h d du uhu ud dhud dr r-=⋅-===2221)1(2222)()(θθθθθd u d uh d du d d hd dudt dh r -=-=-=mu F u d u d u h )()(2222-=+∴θ轨道微分方程 又称比耐（Binet ）公式其中⎩⎨⎧〉〈=) 0 0)(质点散射斥力（引力（万有引力）αr F u F 有心力⇔运动轨道 联系在一起3、平方反比引力—行星的运动 sun M; planet m 222umk rMm GF -=-= 其中GM k =2与行星质量无关，称为太阳的高斯常数， 代入Binet 公式得2222hk u d u d =+θ令22h k u -=ξ则022=+ξθξd d 其解为 )cos(0θθξ-=A 则220)cos(hk A u +-=θθ)cos(1/102222θθ-+==∴kh Ak h ur 其中0,θA 为积分常数，通过坐标变换（极轴转过一角度），使得00=θ 则得轨道方程 θcos 1e p r +=（圆锥曲线，力心在其焦点处）半正焦弦 22kh p =偏心率 Ap e =当0=θ时，ep r +=1 极小 对应近日点；由解析几何知，e 是几何常数1<e 椭圆 1=e 抛物线 1>e 双曲线※由动力学常数h E ,确定e ，既由E 判定轨道类别，e 与E 的关系？drdV rm k F -=-=22rm k r V 2)(-=， rm k r rm E 2222)(21-+=θ对近日点 0=r ep r +=1 222)1(e ph rh +==θ 代入上式得pe m k e ph e pmE )1()1()1(21244222+-++=)1(2)1(22222e k e h pmE +-+=⇒422111mkEh e +±=+∴ 22)(21kh mE e +=⇒可见 0<E 1<e 椭圆； 0=E 1=e 抛物线； 0>E 1>e 双曲线。

有心力的基本性质

有心力的基本性质

有心力的基本性质
有心力是指一个物体运动时所受到的向心力，它是一种基本的物理力。

有心力的基本性质包括以下几个方面：
有心力是一种向心力，即作用在物体运动轨迹上的一个向心的力。

有心力的大小、方向和作用点都是固定的，它随着物体的运动而不断改变方向，但其大小始终不变。

二、有心力的来源
有心力的来源是物体在运动过程中所受到的惯性力和拉力。

当物体沿着曲线运动时，需要受到向心力来保持其运动状态。

惯性力是物体自身的惯性所产生的，它会使物体朝着惯性方向运动。

拉力则是在物体运动时由外部施加的一种力，它是为了保持物体在其运动轨迹上运动。

三、有心力与速度的关系
有心力与物体的速度有密切关系。

当物体的速度增大时，所受到的向心力也会增强。

这是因为向心力是用来使物体沿曲线运动的，当物体的速度增加时，曲线的半径需要更大才能保持向心力。

因此，向心力与物体的速度成正比。

有心力的方向始终指向物体运动轨迹的圆心，它与速度方向、加速度方向和曲线的切线方向都垂直，所以有心力也被称为径向力。

根据向心力的方向和大小可以确定物体在曲线上的运动状态。

离心力是一种指向物体运动轨迹圆心的向外的力，它是向心力的反作用力。

当物体受到向心力时，它会产生一种离心力，试图使物体逃离圆心。

这是因为向心力产生了一个向圆心的加速度，而离心力产生一个向外的加速度，使物体处于动态平衡状态。

有心力作用下的运动

有心力作用下的运动·有心力问题的基本规律如前所述，力的作用线始终通过某定点的力称为有心力。

该定点称为力心。

显然，物体之间的万有引力，带电粒子之间的库仑力都是有心力。

仅受有心力作用的物体，其运动必定具有以下特征：（1）物体在其初速度和力心所决定的平面内运动。

（2）有心力对其力心的力臂为零。

所以，有心力对其力心的力矩恒为零，物体对力心的角动量守恒。

（3）由于有心力的大小通常只取决于物体与力心的距离，而与方位角无关，可以证明有心力对物体做功只与起点、终点的位置有关，与其间所通过的路径无关，即有心力是保守力（有势力）。

于是，有心力系统的机械能守恒。

这样，由角动量守恒、机械能守恒可以列出研究有心力问题的两个基本方程。

对下面天体运动、粒子散射实例，我们只作定性讨论。

·天体运动－平方反比引力作用下的运动丹麦天文学家第谷.布拉赫（1546－1601）曾经系统地观测星球的位置。

当时望远镜尚未发明，全部观测仅凭肉眼进行，但其测量结果却以高精密度著称。

其测量的不确定度为2'，‘精度比前人高5倍，有的数据甚至沿用至今。

他把大量资料留给了助手开普勒。

开普勒潜心研究，终于突破自古以来认为行星作圆周运动的思想束缚，总结出开普勒行星运动三定律：（1） 行星轨道为椭圆，太阳位于椭圆的一个焦点。

（2） 行星位矢在相等时间内扫过相等面积。

（3） 行星公转周期的平方正比于轨道半长轴的立方。

事实上，由万有引力和引力势能rGMm E r GMm F -=-=P 2, 从系统角动量守恒和机械能守恒容易得出与开普勒相同的结论。

不仅如此，牛顿得出，质点在平方反比有心力作用下，除了椭圆(e <1)运动以外还可能作抛物线(e =1)和双曲线(e >1)运动（图1），天文观测也证实了有些彗星就是按抛物线或接近抛物线的双曲线运动的。

当然，不管是自然天体，还是人造天体，都可以用有心力作用下的运动进行讨论。

由此，还可以解释，为什么银河系和宇宙中的许多星系都具有类似铁饼的扁平涡旋状结构。

(完整版)第五章有心力场中的运动


p3 d 0 (1 cos )2
此式就是质点的运动方程。
式中积分常数为 0，即矢径r与e重合的时刻，称为
过近地点时间。
轨道平面方位（，i）和偏心率矢量e的方位确定后，轨道
方程和时间积分即完全确定二体问题的运动规律。
以上积分过程中出现8个积分常数，E，L，，i，，p，e，
，称为轨道根数，由于有关系式e
mr v F (r) r r 0 r
d (r v) 0
dt
r v L(常矢量）
称为动量矩积分（守恒）。L为单位质量的质点对O的动
量矩。常矢量L垂直于r与v构成的平面，因此质点必永远在此
平面内运动，此平面称为轨道平面。
因此可以采用极坐标来研究问题。
动量矩积分在极坐标中的的标量形式：
上节讨论的二体问题是多体问题中唯一可导出解析积分 的最简单情况。三体问题，即三个相互以万有引力吸引的质 点运动，不存在解析积分。
若三体问题中有一体质量m远小于另外两体的质量m1，m2， 以至于它对后两者运动的影响可以忽略不计，则可以认为m1， m2作为独立的二体运动，只需要讨论m在m1，m2的共同引力场 中的运动。这种简化的三体问题称为限制性三体问题。考虑 地球和月球引力共同作用的航天器运动就是典型的限制性三 体问题。
可以看出e在轨道面内且与速度方向垂直。在近地点e与e
方向一致，在远地点e与e方向相反，在其它位置e与e有夹角。
由此可以得出结论：在近地点或远地点施加冲量对改变偏 心率有最好的效果。
在近地点，e与e一致，使e增
加，轨道椭圆更扁。相反在远地点，
e与e相反，e减小，轨道椭圆更圆。
利用此原理，同步地球卫星的 发射过程设计为先进入近地圆轨道， 然后施加冲量，转移至远地点为同 步卫星高度的椭圆轨道(称为霍曼转 移轨道)，然后在远地点施加冲量使 偏心率减为0，变成以远地点为半径 的同步圆轨道。

《有心力课件》课件

《有心力课件》ppt课 件
contents
目录
• 引言 • 心力的基本概念 • 心力的应用 • 如何提升心力 • 心力的未来发展 • 总结与展望
CHAPTER 01
引言
课程背景
当前社会，随着科技的发展和人们生活节奏的加快，越来越 多的人感到压力巨大，心力不足。为了帮助大家更好地应对 生活中的挑战，提高心理承受能力和自我调节能力，我们特 别推出了《有心力课件》这一课程。
学习中的应用
01
02
03
提高专注力
心力有助于我们更好地集 中注意力，通过排除干扰 和调整心态，提高学习效 率和成绩。
培养兴趣爱好
心力可以帮助我们发现和 培养自己的兴趣爱好，通 过积极探索和学习新知， 丰富个人生活和发展。
应对考试压力
心力可以帮助我们更好地 应对考试压力，通过调整 心态和管理情绪，保持冷 静和自信的状态。
随着心理学的不断发展，心力研究将更加深入和全面。未来的研究将进
一步探讨心力的内在机制、影响因素以及与其他心理品质的关系，为个
体提供更有针对性的提升方案。
02
心力在实践中的应用
心力理论在教育、企业管理、心理咨询等领域具有广泛的应用前景。未
来将进一步探索如何将心力理念融入日常教育和企业管理中，帮助个体
更好地应对挑战和压力。
心力的未来发展
心力研究的现状
01
当前心力研究主要集中在理论探 讨和实验验证方面，取得了一些 重要的研究成果，但仍然存在许 多未知领域和挑战。
02
随着科学技术的不断进步，心力 研究的方法和手段也在不断更新 和完善，这为未来的研究提供了 更多的可能性。
心力未来的发展趋势
心力研究将进一步深化对心理和生理 相互作用的机制，探究心理因素对身 体健康和疾病的影响。

有心力


6
理论力学
质点力学
此时必有： 此时必有：
B
F = −∇V
B r2 A r1
W = ∫ F ⋅ dr = ∫ Fr i ⋅ (dri +rdθ j ) = ∫ Fr dr = −(V2 − V1 )
A
机械能守恒： ∴ 机械能守恒：
1 & & m(r 2 + r 2θ 2 ) + V(r) = E 2 1 & & m(r 2 + r 2θ 2 ) + V(r) = E 2
哈雷慧星
第一章 质点力学
1
理论力学
本节教学目的： 本节教学目的：
质点力学
(1) 掌握有心力的概念和基本性质； 掌握有心力的概念和基本性质； (2) 掌握有心力作用下质点运动轨道满足的方程； 掌握有心力作用下质点运动轨道满足的方程； (3) 掌握两种重要的有心力 与距离平方成反比的引力和 掌握两种重要的有心力:与距离平方成反比的引力和 斥力作用下质点的运动规律及动力学性质. 斥力作用下质点的运动规律及动力学性质 (4) 掌握行星运动规律 掌握行星运动规律——开普勒定律。 开普勒定律。 开普勒定律
1 1 k 2m & E = mv 2 + V ( r ) = m ( r 2 + r 2θ& 2 ) − 2 2 r
k 2m V ( r ) = − r
& r 2θ = h
dr du dθ 1 du du & r= ⋅ ⋅ = - 2 ⋅ hu 2 ⋅ =-h du dθ dt u dθ dθ
c p , ⇒ p = a(1 − e2 ), e < 1 B点： = a − c = a(1 − ) = a(1 − e) = 点 r a 1+ e 13
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第二宇宙速度
3.当 e > 1
E >0
双曲线 脱离太阳
2GM s = 42.2 ×103 m / s Rs
仿照地球： v′ =
地球相对太阳的速度： ve = 30 ×103 m / s
v = v′ − ve = 12 ×103 m / s 12× 行星脱离太阳的速度：
1 2 1 2 k 2m 1 2 1 2 还需克服地球引力： mv3 = mv + = mv + mv2 2 2 R 2 2
开普勒第二定律： dA = 常数 dt
dA ∆A 1 2 ∆θ 1 2 dθ = lim = lim r = r ∆t 2 dt dt ∆t →0 ∆t ∆t →0 2
Байду номын сангаас
& = r 2θ & ∴2A & ∴ mr θ = mh v v ∴r × F = 0
2
& QA=c
& ∴r θ = c
2
v J =c
d 2u 1 2 1 = [ 2 − ] 2 dθ 2a cos θ cosθ
三、平方反比引力－－－行星的运动
1.
用比耐公式求行星的轨道方程 已知
F (r ) ⇒ u → r
k 2 = GM
太阳（M）与行星(m)间的万有引力：
GMm k 2m F = − 2 = − 2 = −mk 2u 2 r r
第三宇宙速度： v = v 2 + v 2 = 16.5 ×103 m / s 3 2
的意义
扫过面积 ∆A = πab
有 h2 p =
4π 2 a 2b 2
τ
τ2
b 2 4π 2 a 3 = 2 a τ
∴ h2 p = c
开普勒第三定律： τ 2 = c
a3
h 2 p 与行星无关. 结论：h、p虽与行星有关，但
4. 与万有引力比较
m h2 p k 2m F =− =− 2 2 r r
m h2 p 1 =− ∝− 2 2 r r
说明：行星受力是平方反比引力，但不能说就是万有引 力，因 h、p与行星有关，而万有引力中 k 2 = GM 与行星无关.
3. 由开普勒第三定律说明 h 2 p 设行星运行周期 ∆ t = τ 由
dA 1 2 & 1 = rθ= h dt 2 2 h= 2πab
已知
r = r (θ ) ⇔ F ( r )
“ +”斥力 F “ −”引力
例题 证明：质点受有心力作用做圆 r = 2a cosθ 的运动，则
解：根据
8ma 2 h 2 F =− r5 d 2u − mhu 2 ( 2 + u ) = F dθ
u= 1 1 = r 2a cosθ
du 1 sin θ = dθ 2a cos 2 θ
2k 2 2 4 2 e = 1 + h k ⋅ (v0 − ) r0
讨论
1.
当
e=0
E <1
圆形轨道 第一宇宙速度
k GM v0 = = ≈ Rg = 7.9 × 103 m / s r0 r0
e =1
E =0
沿抛物线轨道飞出，脱离地球
1 2 k 2m mv0 − =0 2 r0
2k 2 2GM v0 = = = 2 Rg = 11.2 × 103 m / s r0 R
v ∴M = 0
v F ≠0
行星有加速度，
所以：r必与F共线，行星必受有心力作用，太阳是力心
2. 由开普勒第一定律求行星受力量值
p 第一定律： r = 1 + e cosθ
du e = − sin θ dθ p
u=
1 e + cosθ p p
d 2u e = − cosθ 2 dθ p
d 2u 2 2 1 2 F = −mhu ( 2 + u ) = −mh u p dθ
§1.9
有心力
一、有心力的基本性质 1. 有心力定义 方向：质点在运动中受力的方向总通过某固定点 o 力心 v 大小：矢径 r 的函数 F (r ) 2. 质点始终在一平面内运动 用两个坐标表示：
( x, y )
或
( r ,θ )
v v r F (r ) = F (r ) r
3. 基本方程
v v && = F (r ) r mr r
讨论：
e <1 e =1 e >1
椭圆 抛物线 双曲线
3. 用能量守恒求轨道 引力势能
k 2m k 2m V = − ∫ F (r )dr = ∫ 2 dr = − ∞ r r
r
机械能守恒 角动量守恒
{ r θ& = h
2
1 k 2m 2 2 &2 & m(r + r θ ) − =E 2 r
dr r 2 E 2 = r − h 2 + 2k 2 r dθ h m
解：
r=
h2 k 2 1 + 1 + 2 h 2 E k 4 m ⋅ cos(θ − θ 0 )
两种方法结果比较
2E h 2 e = 1+ ( 2) m k
e的物理于意义
e <1 e =1 e >1
E<0 E =0 E >0
椭圆 抛物线 双曲线
说明：轨道的形状由总能量E决定，而E守恒，所以
1 2 k 2m E = E0 = mv0 − 2 r0
2
k =h p =
2 2
4π a
2
3
τ2
3 2
行星运动周期
2πa τ= k
五、宇宙速度与宇宙航行 人造卫星运动轨道
r=
h2 k 2 1 + 1 + 2 h 2 E k 4 m ⋅ cosθ
1 2 k 2m E = E0 = mv0 − 2 r0
r=
h2 k 2 2k 2 2 1 + 1 + h 2 k 4 ⋅ (v0 − ) ⋅ cosθ r0
初始能量决定
四、开普勒定律 第一定律：行星绕太阳作椭圆运动，太阳位于椭圆的一 个焦点上. 第二定律：行星和太阳之间的联线 （矢径），在相等时 间所扫过面积相等. 第三定律：行星公转的周期的平方和轨道半长轴的立方 成正比. 后来，牛顿发表了万有引力定律。
从开普勒定律推出万有引力定律
1.
由开普勒第二定律得出行星受有心力作用
& (r θ ) = 0
2
动量矩守恒
4. 有心力是保守力
证明
2
v ∇× F = 0
机械能守恒 1 m(r 2 + r 2θ 2 ) + V (r ) = E & & 二、轨道微分方程（比耐公式）
& m(&& − rθ ) = F (r ) r 2& r θ = h
由方程
d 2u − mhu 2 ( 2 + u ) = F 可证明： dθ
分量形式
直角坐标：
x m&& = F (r ) x r m&& = F (r ) y y r
极坐标：
& m(&& − rθ ) = F (r ) r & && m(rθ& + 2rθ ) = Fθ = 0
(1) ( 2)
（2）式物理意义： 1 d
m
r dt 2 & mr θ = mh v v r × mv = mh
由比耐公式：
d 2u hu 2 ( 2 + u ) = k 2u 2 dθ
A、θ 0 由初始条件定
k2 方程解： u = A cos(θ − θ 0 ) + 2 h
轨道方程
h2 k 2 r= 1 + A h 2 k 2 cos(θ − θ 0 )
θ0 = 0
圆锥曲线的标准方程
适当选取坐标原点可使
h2 k 2 p r= = 2 2 1 + A h k cosθ 1 + e cosθ