工科数学分析下考试题带答案

,考试作弊将带来严重后果！华南理工大学期末考试《工科数学分析》2017—2018学年第二学期期中考试卷1. 考前请将密封线内填写清楚；所有答案请直接答在试卷上(或答题纸上)； ．考试形式：开（闭）卷；本试卷共 4个 大题，满分100分， 考试时间90分钟。

10分，共60分）设函数f 有二阶连续偏导数,求函数22,x z f x y y ⎛⎫=+ ⎪⎝⎭的二阶混合偏导数.解:12212222211122223212,4112+24+210z f x f x yf f z x f x y y y y y f x xxyf f f y y y ∂''=⋅+⋅∂''∂∂∂-'=⋅+⋅∂∂∂∂'⎛⎫''''''=--- ⎪⎝⎭计算 2421222xxxdx dy dx dy yyππ+⎰⎰:()22421221322sin724210xy yx x dx dy dx dyyyx dy dx yπππππ+==+⎰⎰⎰⎰分分计算体密度为ρ=:z ∑=与1z =所围成立体的质量。

解：在球坐标下1z =即1cos 1,cos z r r ϕϕ===，z ∑=：cos sin r r ϕϕ==，进而tan 1,cos 04πϕϕϕ=≥⇒=。

z ∑=：1z =交线即221,1x y z +==得立体投影域22:1xy D x y +≤含原点。

从而立体1:02,0,04cos r πθπϕϕΩ≤≤≤≤≤≤，2分 用球坐标计算质量()1/cos 2/4201/cos /430sin 72sin 1106m d d r r drd r dr ϕππϕπθϕϕπϕϕπΩ==⋅==⎰⎰⎰⎰⎰4. 计算()221(1)Lx dy ydx x y ---+⎰，其中L 为下列闭曲线，沿逆时针方向：（1）点()1,0在L 所围区域之外；（2）点()1,0在L 所围区域之内。

09级《工科数学分析》(下)试题A 参考答案一．填空题（每小题4分，总12分。

将答案按题号写在答题纸上，不写解题过程）1、222,0y C Cx C =+≥的常数；2、3 ；3、0 ，34-. 二．选择题（每小题4分，总12分。

每小题给出四种选择，有且仅有一个是正确的，将你认为正确的代号按题号写在答题纸上）1、C;2、B ；3、B.三（7分）、解：sin ,xz f e y x ∂'=∂2222sin sin ;x x z f e y f e y x∂'''=+∂ 同理2222sin cos ;x x zf ey f e y y∂'''=-+∂结合已知得0.f f ''-=解这个常微分方程得 1212(),,t t f t C e C e C C -=+为任意常数。

四（8分）、解：设32(18)F x y z x y z λ=+++-，令2233230200180x y z F x y z F x yz F x y F x y z λλλλ⎧=+=⎪=+=⎪⎨=+=⎪⎪=++-=⎩，解出9,6,3x y z ===由题意知最大产出必存在，所以9,6,3x y z ===为所求。

五（7分）、解：令23zF z e xy =-+-，则有()2|4,x P F P y '==()2|2,y P F P x '==()(1)|0.z z P F P e '=-=故 切平面方程为4(1)2(2)0(0)0x y z -+-+⋅-= 即 240x y +-= 法线方程120420x y z ---==即 120.210x y z ---== 六（8分）、解：依题意令密度函数为k ρ=为待定常数。

由球体的对称性只需求其对z 轴的转动惯量22()d z I x y V ρΩ=+⎰⎰⎰即可。

又由题设m dV ρΩ=⎰⎰⎰。

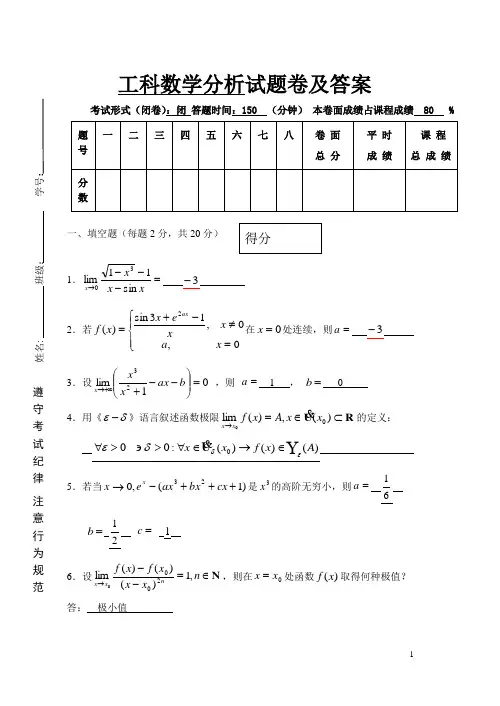
工科数学分析试题卷及答案考试形式（闭卷）：闭 答题时间：150 （分钟） 本卷面成绩占课程成绩 80 %一、填空题（每题2分，共20分）1．---→xx x x sin 11lim 30 3-2．若⎪⎩⎪⎨⎧=≠-+=0,0,13sin )(2x a x xe x xf ax 在0=x 处连续，则a 3- 3．设01lim 23=⎪⎪⎭⎫⎝⎛--++∞→b ax x x x ，则 =a 1 ， =b 0 4．用《δε-》语言叙述函数极限R U ⊂∈=→)(,)(lim 0x x A x f x x 的定义： εδδε)()()(:000A x f x x ∈→∈∀>∍>∀U 5．若当)1(,023+++-→cx bx ax e x x是3x 的高阶无穷小，则=a61=b21=c 1 6．设N ∈=--→n x x x f x f nx x ,1)()()(lim2000，则在0x x =处函数)(x f 取得何种极值？ 答： 极小值姓名: 班级： 学号：遵守 考 试 纪 律 注 意 行 为 规 范7．设x x y +=，则dydx x)211(+⋅8．设x x y sin =，则=dy dx xxx x xx)sin ln (cos sin +9．⎰=+dx x x 21arctan C x +2arctan 21 10．⎰=+dx ee xx12 C e e x x ++-)1l n ( 二、选择题：（每题2分，共20分）1．设0,2)1()1l n (2s i n2t a n li m 2222≠+=-+-+-→c a e d x c xb x a x x ，则必有（ D ）（A ）d b 4=；（B ）c a 4-=；（C ）d b 4-=；（D ）c a 2-= 2．设9320:0<<>k x ，则方程112=+x kx 的根的个数为（ B ）（A ）1 ；（B ） 2 ； （C ） 3 ； （D ）03．设)(x f 连续，且0)0(>'f ，则存在0>δ使得（ A ）（A ）)(x f 在),0(δ内单增； （B ）对),0(δ∈∀x 有)0()(f x f >； （C ）对)0,(δ-∈∀有)0()(f x f >； （D ）)(x f 在)0,(δ-内单减。

河南理工大学 2010-2011 学年第 2 学期《工科数学分析》(下)试卷（A 卷）一、填空题（共28分，每小题4分）１．函数xyz z xy u -+=32在点()2,1,1处沿方向l （其方向角分别是00060,45,60）的方向导数 是 9/2 ．２．设0 < p < 1，计算级数()∑∞=--1121k k p p k =)20(,22<<-p pp3. 函数())sin(,22y x y x f +=在点)0,0(的泰勒公式（到二阶为止）为()()()2222,y x y x y x f +=++=ρρο４．函数()xx f 3=的幂级数展开式为∑∞=0!3ln n nn x n ．5.设()⎰-=22x xxy dy ex F ,则=')(x F ()⎰----+-223522x xxy x x dy ey ex e６．()⎰C ds x =()15532-，其中（C ）为抛物线x y =从点()0,0到点()1,1的一段弧。

7．微分方程()02='+''y y ，满足初始条件1,000='===x x y y 的特解为1ln y +=x 。

二、解答题（共50分，每小题10分）1、 设()v u ,Φ具有连续偏导数，函数()y x z ,由隐方程()bz cy az cx --Φ,=0确定，求yz b x z a∂∂+∂∂。

解：将隐方程两边全微分可得：()()()()()0,2121=-⋅Φ'+-⋅Φ'=-⋅Φ'+-⋅Φ'=--Φbdz cdy adz cdx bz cy d az cx d bz cy az cx d ………………………………………………3分 整理得：dy b a c dx b a c dz 212211Φ'+Φ'Φ'+Φ'+Φ'Φ'=……………………………………6分所以，212211,Φ'+Φ'Φ'=∂∂Φ'+Φ'Φ'=∂∂b a c y zb ac x z …………………………………………8分 y zb x z a ∂∂+∂∂=c b a c b b a c a =Φ'+Φ'Φ'+Φ'+Φ'Φ'212211,………………………………………10分2、 判定正项级数∑⎰∞=+1141n n dx x x的敛散性。

2009-2010第二学期工科数学分析期末试题解答(A 卷)一.1.11,65arccos(2分,2分)2.(1,2,7),4(2分,2分)3.25-,}52,51{-(2分,2分)4.∑∞=+--01)1(4)1(n nn n x ,∑∞=---+11)1(4)1(4ln n nn n x n (2分,2分)5.dy dx 2-,}2,1{-(2分,2分)6.x x y ln ,34ln(2分,2分)7.0，ππ324+，0，12+π(1分，1分，1分，1分)二.⎰=Ly dlx I μ2…………………….(2分)⎰+=15322)1(1dxx x μ……………………(6分)μμ35611532=+=⎰dx x x ……………………(9分)三.设V 在第一卦限部分为1V ⎰⎰⎰⎰⎰⎰==122486V VdVx dV x I ……………(3分)⎰⎰⎰---=yx xdzdy dx x 101010248……………..(6分)⎰⎰---=xdyy x dx x 10102)1(48………………..(7分)⎰-=1022)1(24dx x x …………………(8分)54=…………………(9分)四.令02==∂∂x xz，014=-=∂∂y yz………………(2分)解得0=x ,41=y ,得驻点)41,0(,………………..(3分)由122=+y x ，得221y x -=，代入目标函数得62+-=y y z )11(≤≤-y ………………..(4分)令012=-=y dydz，得21=y ，此时23±=x ，得两点)21,23(±………..(6分)当1±=y 时，0=x ，得两点)1,0(±………………..(7分)83941,0(=z ，42321,23(=±z ，8)1,0(=-z ，6)1,0(=z 8max =z ，839min =z ……………..(9分)五．由题意,有yXx Y ∂∂=∂∂……………………….(1分)λλλλλλλλ2121)()()33()(3)()()3()(3y x y x y y x y x y x x y y x ++--+=++--+---…….(3分)即033=--+y x y x λλ，3=λ…………………….(4分)1),()1,1(33)(3)(3),(C dy y x xy dx y x x y y x u y x ++-++-=⎰…………………….(6分)11313)(3)(3C dy y x x y dx y x xy x++-++-=⎰⎰……………………(8分)C y x yx ++-=2)(……………………(10分)注：没有加C 不扣分。

工科数学分析（下）北京航空航天大学智慧树知到答案2024年第一章测试1.A:图中C B:图中A C:图中B D:图中D答案:B2.A:图中C B:图中D C:图中B D:图中A答案:A3.A:图中C B:图中A C:图中D D:图中B答案:B4.A:图中B B:图中D C:图中C D:图中A答案:A5.A:图中A B:图中B C:图中C D:图中D答案:D6.A:图中B B:图中A C:图中C D:图中D答案:B7.A:图中A B:图中C C:图中DD:图中B答案:C8.A:图中DB:图中B C:图中C D:图中A答案:A9.A:图中A B:图中C C:图中B D:图中D答案:A10.A:图中B B:图中C C:图中D D:图中A答案:D第二章测试1.A:图中A B:图中C C:图中B D:图中D答案:A2.A:(3)错 B:全错 C:(1)错 D:(2)错答案:C3.A:图中A B:图中B C:图中D D:图中C答案:A4.A:图中B B:图中A C:图中D D:图中C答案:AA:图中B B:图中D C:图中C D:图中A答案:D第三章测试1.A:图中C B:图中B C:图中A D:图中D答案:C2.A:图中C B:图中A C:图中D D:图中B答案:B3.A:图中C B:图中D C:图中A D:图中B答案:D4.A:图中B B:图中D C:图中A D:图中C答案:C5.A:图中B B:图中D C:图中C D:图中A答案:D6.A:图中D B:图中C C:图中A D:图中B答案:D7.A:图中C B:图中A C:图中D D:图中B答案:C8.A:图中D B:图中C C:图中B D:图中A答案:D9.A:图中B B:图中C C:图中A D:图中D答案:A10.A:图中D B:图中C C:图中B D:图中A答案:D第四章测试1.A:图中D B:图中B C:图中A D:图中C答案:C2.A:图中B B:图中A C:图中D D:图中C答案:B3.A:图中A B:图中B C:图中C D:图中D答案:B4.A:图中C B:图中B C:图中D D:图中A答案:B5.A:图中C B:图中A C:图中B D:图中D答案:D6.A:图中B B:图中C C:图中D D:图中A答案:D7.A:图中C B:图中B C:图中A D:图中D答案:C8.A:9 B:1 C:3 D:-1答案:C9.A:图中B B:图中C C:图中A D:图中D答案:C10.A:图中C B:图中A C:图中D D:图中B答案:C第五章测试1.A:图中A B:图中C C:图中D D:图中B答案:A2.A:图中B B:图中C C:图中A D:图中D答案:C3.A:图中C B:图中B C:图中A D:图中D答案:D4.A:图中C B:图中D C:图中A D:图中B答案:C5.A:图中D B:图中B C:图中A D:图中C答案:C第六章测试1.A:图中B B:图中D C:图中C D:图中A答案:D2.A:图中C B:图中B C:图中D D:图中A答案:C3.A:图中D B:图中C C:图中B D:图中A答案:D4.A:图中B B:图中A C:图中D D:图中C答案:D5.A:图中B B:图中C C:图中A D:图中D答案:B第七章测试1.A:图中B B:图中A C:图中D D:图中C答案:C2.A:图中A B:图中C C:图中D D:图中B答案:B3.A:图中A B:图中D C:图中C D:图中B答案:B4.A:图中B B:图中D C:图中A D:图中C答案:B5.A:图中A B:图中C C:图中B D:图中D答案:C第八章测试1.A:图中D B:图中C C:图中A D:图中B答案:A2.A:图中A B:图中D C:图中C D:图中B答案:B3.A:图中A B:图中B C:图中C D:图中D答案:B4.A:图中D B:图中B C:图中C D:图中A答案:A5.A:图中D B:图中C C:图中B D:图中A答案:D第九章测试1.A:图中D B:图中A C:图中B D:图中C答案:B2.A:图中D B:图中C C:图中A D:图中B答案:B3.A:图中D B:图中A C:图中B D:图中C答案:A4.A:图中A B:图中C C:图中D D:图中B答案:A5.A:图中B B:图中A C:图中D D:图中C答案:B第十章测试1.A:图中D B:图中B C:图中C D:图中A答案:C2.A:图中A B:图中C C:图中D D:图中B答案:D3.A:图中B B:图中D C:图中C D:图中A答案:B4.A:图中B B:图中C C:图中A D:图中D答案:D5.A:图中A B:图中D C:图中C D:图中B答案:C。

工科数学分析（下）期末考试模拟试题姓名：___________得分: _________一、填空题（每小题3分，满分18分）1、设()xz y x z y x f ++=2,,，则()z y x f ,,在()1,0,1沿方向→→→→+-=k j i l 22的方向导数为_________.2.,,,-__________.222L L xdy ydx L x y=⎰+Ñ设为一条不过原点的光滑闭曲线且原点位于内部其走向为逆时针方向则曲线积分1,()cc x y x y ds +=+=⎰Ñ3.设曲线为则曲线积分 ___________4、微分方程2(3xy y)dx 0x dy +-=的通解为___________5、2sin(xy)(y)______________.y yF dx x=⎰的导数为 6、{,01,0x (x),2x e x f x ππππ--≤<≤≤==则其以为周期的傅里叶级数在点处收敛于_____________.二、计算下列各题（每小题6分，满分18分） 1. (1) 求极限lim0→→y x ()xy yx y x sin 11232+-(2) 220)(lim 22y x x y x y +→→2.设f ，g 为连续可微函数，()xy x f u ,=，()xy x g v +=，求xvx u ∂∂⋅∂∂（中间为乘号）.3..222V z x y z V +=设是由所围成的立体,求的体积.三、判断积数收敛性（每小题4分，共8分）1. ∑∞=1!.2n n n nn2.∑∞=-1!2)1(2n n nn四、（本小题8分）求向量场2(23)()(2)x z xz y y z =+-+++A i j k u r r r u r 穿过球面∑： 222(3)(1)(2)9x y z -+++-=流向外侧的通量； 五、（本小题7分）2(1sin )cos ,(0,1)(0,1)y y lx e x dy e xdx l x A B +--=-⎰计算其中为半圆到的一段弧。

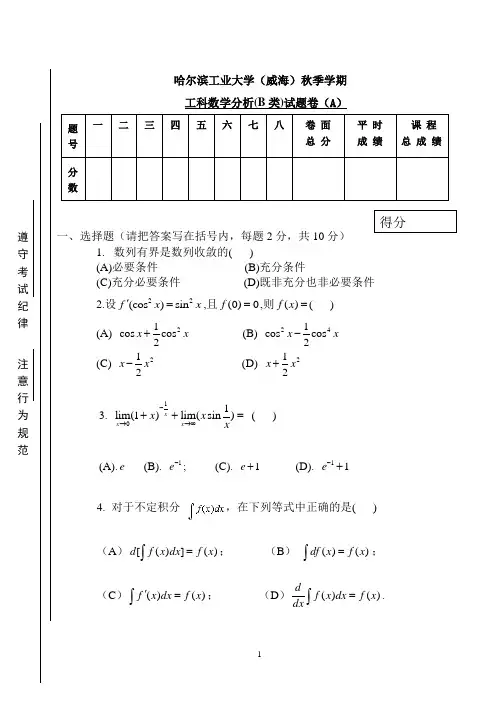
哈尔滨工业大学（威海）秋季学期工科数学分析(B 类)试题卷（A ）题号 一二三四五六七八卷 面 总 分 平 时 成 绩 课 程 总 成 绩分数一、选择题（请把答案写在括号内，每题2分，共10分）1. 数列有界是数列收敛的( )(A)必要条件 (B)充分条件(C)充分必要条件 (D)既非充分也非必要条件2.设22(cos )sin f x x '=,且(0)0f =,则()f x =( )(A) 21cos cos 2x x + (B) 241cos cos 2x x -(C) 212x x - (D) 212x x +3. 11lim(1)lim(sin )xx x x x x-→→∞++= ( ) (A).e (B). 1e -; (C). 1e + (D). 11e -+4. 对于不定积分，在下列等式中正确的是( )（A ）[()]()d f x dx f x =⎰； （B ）()()df x f x =⎰；（C ）()()f x dx f x '=⎰； （D ）()()df x dx f x dx =⎰. 得分遵守 考 试 纪 律 注 意 行 为 规 范5. 设()y f x =满足关系式240y y y '''-+=,若0()0f x >且0()0f x '=，则()y f x =在0x 点（ ）.(A).取极大值； (B).取极小值；(C).在某邻域内单调增； (D).在某邻域内单调减.二、填空题（每题2分，共10分） 1. 设,m n 为正整数，且m n <，则0sin()lim (sin )n mx x x →= .2. 设()(1)(2)(2002)f x x x x x =++⋅⋅⋅+，则 (0)f '= .3.定积分0=⎰ .4. 设()()f x g x '=，则微分2[(sin )]d f x = .5.不定积分2= .三、 算题（每题5分，共30分）1. 计算11lim()ln 1x x x x →--.遵守 考 试 纪 律注 意 行 为 规 范2.计算.1 lim(123)n n nn→∞++.3.已知21ln cos arcsin2xy x xx=++求y'.4.求由参数方程sin1cosx t ty t=-⎧⎨=-⎩确定的函数的导数dydx,22d ydx.5.计算积分(1ln)xe x xdxx+⎰.6.计算Iπ=⎰.四、解答下列各题（每题10分，共50分）1.设函数32ln(1),0,arcsin()60,10.sin4axaxxx xf x xe x axxxx⎧⎪+<⎪-⎪⎪==⎨⎪+--⎪>⎪⎪⎩问(1)a为何值时, ()f x在0x=处连续;(2)a为何值时, 0x=是()f x的可去间断点.2.当a为何值时，抛物线y=x2与三直线x = a，x = a+1，y= 0所3.围成的图形面积最小？4.已知1x2x =…, 1n x +=证明数列{}n x 收敛并求其极限.5. 设函数()f x ,()g x 在[,]a b 上连续，在(,)a b 内可导，且()()0f a f b ==，()0g x ≠，试 证：至少存在一个(,)a b ξ∈，使()()()()f g f g ξξξξ''=.5设严格单调递增函数()[,]f x C a b ∈且()0f x ''>，证明：()()()()()()2ba f a fb b a f a f x dx b a +-<<-⎰遵守 考 试 纪 律注 意 行 为 规 范哈尔滨工业大学（威海）秋季学期 工科数学分析(B 类)试题卷（A ）答案一. (1).A (2).C (3).D (4).D (5)A二(1).0 (2).2002! (3)π(4)2(sin )sin 2g x x(5)35224235x x C ++三1. 11ln 1ln ()lim lim limln 1(1)ln (1)ln(11)111x x x x x x xx x x x x x x x x -----==---+-→→→211ln lim(1)x x x xx →--=-1ln 11lim 2(1)21x x x --==--→ 2．解：因为1113(3)(123)(33)n nn n nnn=≤++≤⨯=3lim n →∞=，所以1(123)3lim nn nn →∞++= 3．223211tan 2arcsin 22(1)x y x x x x x '=-++-+ 4．sin 1cos dydy t dt dx dx t dt==-， 22411()()()2sin 2d y d dy d dy dt d dy dx t dx dx dt dx dx dt dx dxdt ====- 5．(1ln )ln ln ln ln x x x x x x x xx e x x e e e e dx dx e xdx dx xde dx e x dx x x x x xe x C+=+=+=+-=+⎰⎰⎰⎰⎰⎰⎰6.202cos sin sin cos sin cos 1x xdx x xdx x xdx πππππ==-=⎰⎰⎰⎰四．解答题 1.解33200000000ln(1)3(00)()lim lim lim limarcsin arcsin 1x x x x ax ax ax f f x x x x x →-→-→-→-+-====---003(16lim x a a →-=-=-22200000011(00)()4lim lim lim sin4ax ax x x x e x ax e x ax f f x x x x →+→+→++--+--+=== 2220000002224442(2)lim lim lim 222ax ax ax x x x ae x a a e a e a x →+→+→++-++====+令(00)f +=(00)(0)f f -=得1a =-，从而当1a =-时()f x 在0x =连续； 令(00)f +=(00)(0)f f -≠得2a =-，从而当2a =-时0x =是()f x 的可去间断点。