下载文档原格式
哈尔滨工业大学2004 /2005 学年 秋 季学期工科数学分析期末考试试卷 （答案）试卷卷（A ）考试形式（开、闭卷）：闭答题时间：150（分钟） 本卷面成绩占课程成绩70%一．选择题（每题2分，共10分）1．下列叙述中不正确者为（D ）（A ）如果数列}{n x 收敛，那么数列}{n x 一定有界。
（B ）如果a unn lim =∞→，则一定有a u n n lim =∞→。
（C ）f(x)在点0x 处可导的充要条件是f(x)在点0x 处可微。
（D ）如果函数 f(x)=y 在点0x 处导数为0，则必在该点处取得极值。
2．设在[0，1]上0)x (f ''>则下列不等式正确者为（ B ）（A ）)0(f )1(f )0(f )1(f ''->>（B ）)0(f )0(f )1(f )1(f ''>-> （C ）)0(f )1(f )0(f )1(f ''>>-（D ）)0(f )1(f )0(f )1(f ''>-> 3．若f(x)在[]b a,上可积，则下列叙述中错误者为（D ） （A ）dt )t (f xa⎰连续（B ）)x (f 在[]b a,上可积（C ）f(x)在[]b a,上由界（D ）f(x)在[]b a,上连续姓名: 班级： 学号：4．若sinF(x)=dy ])tdt sin sin[(xay03⎰⎰，则=)x (F '（D ）（A ）dy ])tdt sin sin[(cos xay 03⎰⎰（B ）cosx x 3sin )tdt sin sin(dy ])tdt sin sin[(cos 2y3xa y 03⋅⋅⋅⎰⎰⎰（C ）⎰⎰⎰⋅y3xa y 03)x dx sin sin(dy ])tdt sin sin[(cos（D ）⎰⎰⎰⋅y3xay3)tdt sin sin(dy ])tdt sin sin[(cos5．=+∞→)x1e (x 1n lim （D ） （A ）e （B ）2e （C ）3e （D ）4e二．填空题（每题2分，共10分） 1．)0x (x11y n n lim ≥+=∞→的间断点为：1x =，其类型为：第一类间断点。
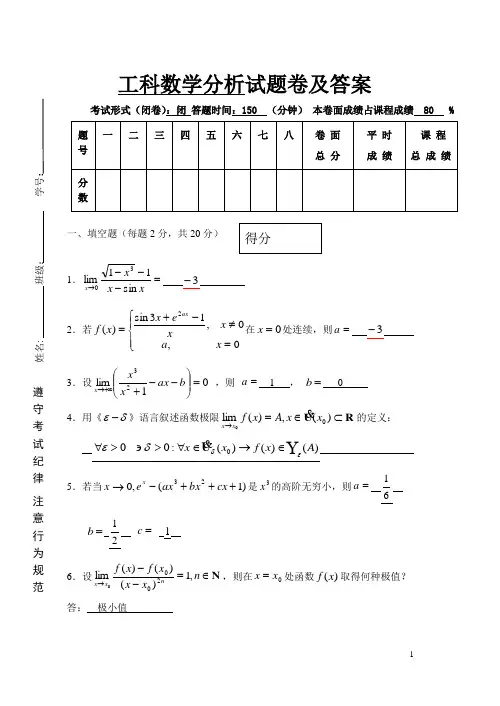
工科数学分析试题卷及答案考试形式（闭卷）：闭 答题时间：150 （分钟） 本卷面成绩占课程成绩 80 %一、填空题（每题2分，共20分）1．---→xx x x sin 11lim 30 3-2．若⎪⎩⎪⎨⎧=≠-+=0,0,13sin )(2x a x xe x xf ax 在0=x 处连续，则a 3- 3．设01lim 23=⎪⎪⎭⎫⎝⎛--++∞→b ax x x x ，则 =a 1 ， =b 0 4．用《δε-》语言叙述函数极限R U ⊂∈=→)(,)(lim 0x x A x f x x 的定义： εδδε)()()(:000A x f x x ∈→∈∀>∍>∀U 5．若当)1(,023+++-→cx bx ax e x x是3x 的高阶无穷小，则=a61=b21=c 1 6．设N ∈=--→n x x x f x f nx x ,1)()()(lim2000，则在0x x =处函数)(x f 取得何种极值？ 答： 极小值姓名: 班级： 学号：遵守 考 试 纪 律 注 意 行 为 规 范7．设x x y +=，则dydx x)211(+⋅8．设x x y sin =，则=dy dx xxx x xx)sin ln (cos sin +9．⎰=+dx x x 21arctan C x +2arctan 21 10．⎰=+dx ee xx12 C e e x x ++-)1l n ( 二、选择题：（每题2分，共20分）1．设0,2)1()1l n (2s i n2t a n li m 2222≠+=-+-+-→c a e d x c xb x a x x ，则必有（ D ）（A ）d b 4=；（B ）c a 4-=；（C ）d b 4-=；（D ）c a 2-= 2．设9320:0<<>k x ，则方程112=+x kx 的根的个数为（ B ）（A ）1 ；（B ） 2 ； （C ） 3 ； （D ）03．设)(x f 连续，且0)0(>'f ，则存在0>δ使得（ A ）（A ）)(x f 在),0(δ内单增； （B ）对),0(δ∈∀x 有)0()(f x f >； （C ）对)0,(δ-∈∀有)0()(f x f >； （D ）)(x f 在)0,(δ-内单减。
习题6.11．（1）（a ）23()()()d ()d ,x y x y σσσσ+>+⎰⎰⎰⎰ （b ）23()()()d ()d ,x y x y σσσσ+<+⎰⎰⎰⎰（2）(a)2()()e d e d xyxy σσσσ<⎰⎰⎰⎰， （d ）2()()e d e d xy xy σσσσ>⎰⎰⎰⎰2．（1）02I ≤≤； （2）0I ≤≤ （3）e I ππ≤≤ （4）3075I ππ≤≤习题6.21．（1）221； （2）3221； （3）4(3115-； （4）62e 9e 4--；（5）54ln 22-； （6）425-； （7）21)15； （8）3cos1sin1sin 42+-2．（1）2 44 04d (,)d d (,)d yy xI x f x y y y f x y x ==⎰⎰⎰⎰；（2） sin 1 arcsin 0 0 0 arcsin d (,)d d (,)d ;xyyI x f x y y y f x y x ππ-==⎰⎰⎰⎰（3）()()()⎰⎰⎰⎰⎰⎰+==21212121211d ,d d ,d d ,d yyxxx y x f y x y x f y y y x f x I（4）21 01 01 21d (,)d d (,)d I x f x y y y f x y x ---==⎰⎰⎰⎰.3．（1）2 10 d (,)d xx x f x y y ⎰⎰； （2） 1 0d (,)d y f x y x ⎰⎰； （3） 1eed (,)d y y f x y x ⎰⎰；（4）1220 0 1d (,)d d (,)d xxx f x y y x f x y y -+⎰⎰⎰⎰； （5） 132 0d (,)d yy f x y x -⎰；（6）22 2 2 00 22d (,)d d (,)d d (,)d aa aa aay y a aaay f x y x y f x y x x f x y x +++⎰⎰⎰⎰⎰⎰；（7）214d (,)d yy f x y x -⎰⎰； （8） 12 01d (,)d yy f x y x -⎰⎰。
工科数学分析（下）期末考试模拟试题姓名：___________得分: _________一、填空题（每小题3分，满分18分）1、设()xz y x z y x f ++=2,,，则()z y x f ,,在()1,0,1沿方向→→→→+-=k j i l 22的方向导数为_________.2.,,,-__________.222L L xdy ydx L x y=⎰+Ñ设为一条不过原点的光滑闭曲线且原点位于内部其走向为逆时针方向则曲线积分1,()cc x y x y ds +=+=⎰Ñ3.设曲线为则曲线积分 ___________4、微分方程2(3xy y)dx 0x dy +-=的通解为___________5、2sin(xy)(y)______________.y yF dx x=⎰的导数为 6、{,01,0x (x),2x e x f x ππππ--≤<≤≤==则其以为周期的傅里叶级数在点处收敛于_____________.二、计算下列各题（每小题6分，满分18分） 1. (1) 求极限lim0→→y x ()xy yx y x sin 11232+-(2) 220)(lim 22y x x y x y +→→2.设f ，g 为连续可微函数，()xy x f u ,=，()xy x g v +=，求xvx u ∂∂⋅∂∂（中间为乘号）.3..222V z x y z V +=设是由所围成的立体,求的体积.三、判断积数收敛性（每小题4分，共8分）1. ∑∞=1!.2n n n nn2.∑∞=-1!2)1(2n n nn四、（本小题8分）求向量场2(23)()(2)x z xz y y z =+-+++A i j k u r r r u r 穿过球面∑： 222(3)(1)(2)9x y z -+++-=流向外侧的通量； 五、（本小题7分）2(1sin )cos ,(0,1)(0,1)y y lx e x dy e xdx l x A B +--=-⎰计算其中为半圆到的一段弧。
工科数学分析（上）提高版北京航空航天大学智慧树知到答案2024年第一章测试1.A:图中D B:图中A C:图中B D:图中C答案:B2.A:图中A B:图中D C:图中B D:图中C答案:C3.A:图中A B:图中C C:图中B D:图中D答案:B4.A:图中D B:图中C C:图中B D:图中A答案:D5.A:图中B B:图中D C:图中C D:图中A答案:D第二章测试1.A:图中C B:图中B C:图中A D:图中D答案:C2.A:图中D B:图中A C:图中B D:图中C答案:D3.A:图中D B:图中C C:图中B D:图中A答案:D4.A:图中C B:图中B C:图中D D:图中A答案:D5.A:图中C B:图中B C:图中A D:图中D答案:A第三章测试1.A:图中D B:图中C C:图中A D:图中B答案:C2.A:图中A B:图中D C:图中C D:图中B答案:A3.A:图中D B:图中A C:图中BD:图中C答案:D4.A:图中A B:图中B C:图中C D:图中D答案:C5.A:图中C B:图中D C:图中A D:图中B答案:D第四章测试1.A:图中C B:图中A C:图中D D:图中B答案:C2.A:图中D B:图中C C:图中B D:图中A答案:D3.A:图中B B:图中D C:图中A D:图中C答案:B4.A:图中C B:图中A C:图中D D:图中B答案:A5.A:图中D B:图中A C:图中B D:图中C答案:B第五章测试1.A:图中A B:图中C C:图中D D:图中B答案:C2.A:图中A B:图中B C:图中C D:图中D答案:A3.A:图中B B:图中A C:图中D D:图中C答案:C4.A:图中B B:图中C C:图中A D:图中D答案:B5.A:图中C B:图中D C:图中A D:图中B答案:B第六章测试1.A:图中B B:图中C C:图中D D:图中A答案:A2.A:图中D B:图中B C:图中C D:图中A答案:D3.A:图中A B:图中D C:图中B D:图中C答案:B4.A:图中D B:图中A C:图中B D:图中C答案:B5.A:图中AB:图中B C:图中D D:图中C答案:D第七章测试1.A:图中B B:图中D C:图中C D:图中A答案:C2.A:图中B B:图中D C:图中C D:图中A答案:A3.A:图中C B:图中B C:图中D D:图中A答案:D4.A:图中A B:图中D C:图中B D:图中C答案:D5.A:图中D B:图中C C:图中B D:图中A答案:D第八章测试1.A:图中B B:图中A C:图中C D:图中D答案:D2.A:图中A B:图中C C:图中D D:图中B答案:B3.A:图中D B:图中A C:图中B D:图中C答案:B4.A:图中A B:图中C C:图中B D:图中D答案:A5.A:图中D B:图中B C:图中A D:图中C答案:C第九章测试1.A:图中B B:图中C C:图中D D:图中A答案:C2.A:图中D B:图中B C:图中C D:图中A答案:C3.A:图中B B:图中C C:图中D D:图中A答案:D4.A:图中C B:图中B C:图中A D:图中D答案:C5.A:图中B B:图中D C:图中A D:图中C答案:D。
2004-2005学年秋季学期工科数学分析答案哈尔滨工业大学2004 /2005 学年 秋 季学期工科数学分析期末考试试卷 （答案） 试题卷（A ） 考试形式（开、闭卷）：闭答题时间：150（分钟） 本卷面成绩占课程成绩70%题号一 二 三 四 五 六 七 八 卷 面 总 分平时 成 绩 课程 总 成绩分数一．选择题（每题2分，共10分）1．下列叙述中不正确者为（D ） （A ）如果数列}{nx 收敛，那么数列}{nx 一得分姓名: 级：4．若sin F(x)=dy ])tdt sin sin[(xa y3⎰⎰，则=)x (F '（D ）（A ）dy ])tdt sin sin[(cos xay3⎰⎰（B ）cosxx 3sin)tdt sin sin(dy ])tdt sin sin[(cos 2y3xay3⋅⋅⋅⎰⎰⎰（C ）⎰⎰⎰⋅y3xay3)x dx sin sin(dy ])tdt sin sin[(cos（D ）⎰⎰⎰⋅y3xay3)tdt sin sin(dy ])tdt sin sin[(cos5．=+∞→)x1e(x1n lim （D ）（A ）e （B ）2e （C ）3e （D ）4e二．填空题（每题2分，共10分）1．)0x (x11y nn lim ≥+=∞→的间断点为：1x =，其类型为：第一类间断点。
得分遵 守 考 试 纪 律 注 意 行 为 规 范2．23x )(1x y +=的全部渐近线方程为：2-x y 1,x =-=。
3．摆线2t )cost 1(a y )sint t (a x π=⎩⎨⎧-=-=在处的切线方程为：0a )4(21y x =-+-π。
4．2n 1n )!n (lim ∞→=： 1 。
5．设f(x)在[)+∞,1上可导，23e )1e(f , 0f(1)2x x'+=+=，则=：23-+-三．计算下列各题：（每小题4分，本题满分20分）1．若xy 2e x y = ，求?yx'=解：2xylnx lny =+， 2x 'x 'x y x y y y 2-=⋅则)2x y (x )y x (y y x'-+=2．⎪⎩⎪⎨⎧-==)sint t y 2t cosx ，?yxx''=求 解：2t 4sin2t sin 21cost 1x y y t 't 'x '-=--==，2t4cos2t sin 2112t 2cos yxx''=-⋅-=得分3. ⎰+dx 1x x arctan 解：⎰⎰=⎰⋅⋅=⋅⋅+==sectdt ant t 2tdt sec 2tant sectt dx1x x arctan 2t tan x ttan x 2=c tant sect 2ln -sect 2t sectdt 2-2tsect tdsect 2++⋅==⎰⎰=c )x 1x (2ln 1x x 2arctan +++-+⋅ 4．dx e y x 11x⎰--解： dx y)e -(x dx x)e -(y dx e y x 1yxy1x11x⎰⎰⎰+=--- x1yxy1de y)-(x de x)-(y ⎰⎰+=-dxe y)e -(x dx e x)e -(y 1yx 1x y 1-x 1x⎰⎰-++=-yyyee y y )1(e 2]e y)e -(x []e x)e -(y [y 1x x 1x x +-=-++=-5. 已知dt te c x c x c t ⎰∞-∞→=-+2xx )(lim ，求?=c解：t c c t c de t dt te e xc x cc x c x 222x x x x 21)11()(lim lim ⎰⎰∞-∞-∞→∞→==-+=-+=2c2t 2t e )412c (e [te 21-=-⎰∞-∞-c cdt ，所以2c2ce )412(e-=c 。
