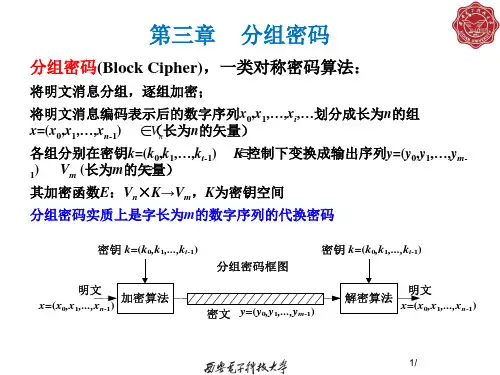
如果对于猜测的密钥和已知的大量明密文对,方程成立的概率p≠1/2,则称该方 程是有效的线性逼近。如果|p-1/2|是最大的,则称该方程是最有效的线性逼近。 等于1/2时说明随机性很好,再多明密文对也不暴露任何信息
21/是使方程左边为0的明文数。 如果T>N/2,则令
此时计算X i X i Yj Yj 就相对直接多了 1 k 1 l
例3.2
我们任然用例3.1中的S盒, s : 0,1 0,1
4
4
在表3.1的行中记下了八个随机变量 X1 , X 4 , Y1 ,Y4
所有可能的取值。 现在考虑随机变量X1 X 4 Y2 通过计算表3.1中 X1 X 4 Y2 0 的行数,可以得到该随机变量取值为零的概率PrX 1 X 4 Y2 0 1 2 1 因此 PrX 1 X 4 Y2 1 可见,该随机变量的偏差为0 再分析随机变量 X 3 X 4 Y1 Y4可看到该随机变量的 偏差为-3/8.
s
p
操作混入该轮的轮密钥,再用 进行m次代换,然后用
1.3 SPN由Nr轮组成,在每一轮(除了最后一轮稍有不同外),我们先用异或
进行一次置换。
密码体制3.1
代换置换网络
lm
l l s : 0,1 0,1 和 设 l , m 和Nr都是正整数, p : 1, lm 1, lm
m n
m
均匀随机的从集合0,1 X ( x1 , x,m ) 中选取,这就 X i 取之于 是说每一个坐标 xi定义了一个随机变量 X i , 0,1
并且其偏差 i 0 。更进一步,这m个随机变量相互独