理论力学第8章(刚体的平面运动)

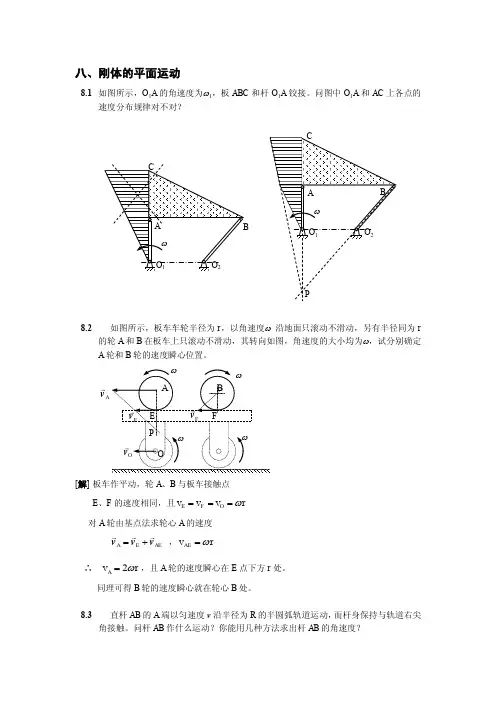
八、刚体的平面运动8.1 如图所示，O 1A 的角速度为ω1，板ABC 和杆O 1A 铰接。

问图中O 1A 和AC 上各点的速度分布规律对不对？8.2如图所示，板车车轮半径为r ，以角速度ω 沿地面只滚动不滑动，另有半径同为r 的轮A 和B 在板车上只滚动不滑动，其转向如图，角速度的大小均为ω，试分别确定A 轮和B 轮的速度瞬心位置。

[解] 板车作平动，轮A 、B 与板车接触点 E 、F 的速度相同，且r v v v O F E ω=== 对A 轮由基点法求轮心A 的速度 A E AE =+v v v ，r v AE ω=∴ r v A ω2=，且A 轮的速度瞬心在E 点下方r 处。

同理可得B 轮的速度瞬心就在轮心B 处。

8.3直杆AB 的A 端以匀速度v 沿半径为R 的半圆弧轨道运动，而杆身保持与轨道右尖角接触。

问杆AB 作什么运动？你能用几种方法求出杆AB 的角速度？E FPOE v Av Fv Ov[解] AB 杆作平面运动。

(一) 瞬心法AB 杆作平面运动，速度瞬心为P 。

Rv AP v AAB2==ω (二)基点法D A DA =+v v v ，DA v v AB A DA ωθ==sin又 DA ＝2R cos(90o －θ)＝2R sin θ ∴ Rv AB 2=ω(三)自然法： d d AB tϕω=，而R S ϕ2= ∴d d 2d d S R v t t ϕ==， d d 2vt R ϕ= ∴ Rv AB 2=ω 8.4如图所示四连杆机构OABO 1中，OA=O 1B=AB/2，曲柄OA 的角速度ω=3rad/s 。

当OA 转到与OO 1垂直时，O 1B 正好在OO 1的延长线上，求该瞬时AB 杆的角速度ωAB 和曲柄O 1B 的角速度ω1。

[解]取AB 为研究对象，AB 作平面运动。

以A 为基点，画B 点速度合成图 由B A BA =+v v v(rad/s)32230sin o==∴⋅=⋅==ωωωωAB OAAB OA v v AB AB ABABBBvvvDAv Dv Dv111cos3022(rad/s)B BAv v OA O Bωωω=︒=⋅=∴=8.5图示曲柄摇机构中，曲柄OA以角速度oω绕O轴转动，带动连杆AC在摇块B内滑动，摇块及与其固结的BD杆绕B铰转动，杆BD长l；求在图示位置时摇块的角速度及D点的速度。

第八章 刚体的平面运动8－1 如图所示，平面图形上两点A ，B 的速度方向可能是这样的吗？为什么?8－2 如图所示已知 ，方向如图； 垂直于。

于是可确定速度瞬心C 的位置，求得：CD ACv v A D = D O CD AC v D O v A D 222==ω这样做对吗？为什么？8－3 如图所示的角速度为 ，板 ABC 和图中铰接。

问图中和 AC 上各点的速度分布规律对不对?8－4 平面图形在其平面内运动，某瞬时其上有两点的加速度矢相同。

试判断下述说法是否正确：（1）其上各点速度在该瞬时一定都相等。

（2）其上各点加速度在该瞬时一定都相等。

8－5 如图所示瞬时，已知 和平行，且＝，问与 、与 是否相等?车轮的角加速度是否等于 ？速度瞬心C的加速度大小和方向如何确定?8－7试证：当 ω=0时，平面图形上两点的加速度在此两点连线上的投影相等。

8－8 如图所示各平面图形均作平面运动，问图示各种运动状态是否可能？图a中，和平行，且=-。

图b中，和都与A，B连线垂直，且和反向。

图c中，沿A，B连线，与A，B连线垂直。

图d中，和都沿A，B连线，且> 。

图e中，和都沿A，B 连线，且< 。

图f中，沿A，B连线。

图g中，和都与AC连线垂直，且> 。

图h中， AB 垂直于AC，沿A，B连线，在AB连线上的投影与相等。

图i中，与平行且相等，即=。

图j中，和都与 AB 垂直，且，在A，B连线上的投影相等。

图k中，，在AB连线上的投影相等。

图l中，矢量与在AB线上的投影相等，在AB线上。

8－9 如图所示平面机构中，各部分尺寸及图示瞬时的位置已知。

凡图上标出的角速度或速度皆为已知，且皆为常量。

欲求出各图中点C的速度和加速度，你将采用什么方法？说出解题步骤及所用公式。

8－10 杆AB作平面运动，图示瞬时A，B两点速度，的大小、方向均为已知，C，D两点分别是， 的矢端，如图所示。

试问（l）AB杆上各点速度矢的端点是否都在直线 CD上?（2）对AB杆上任意一点E，设其速度矢端为H，那么点H在什么位置?（3）设杆AB为无限长，它与CD的延长线交于点P。

6 刚体平面运动微分方程刚体的平面运动可简化成刚体的平面图形S 在某一固定平面内的运动，用3个独立坐标描述。

作用在刚体上的外力可简化为S 平面内的一平面力系F i (=1, 2,…,n )。

设坐标系Oxy 为固定的惯性参考系，Cx ′ y ′为质心平移坐标系，如图8-6所示。

平面图形的运动可用质心坐标x C , y C 和绕质心的转动角ϕ描述。

刚体的绝对运动可分解成跟随质心的平移和相对质心平移坐标系的转动。

由动量定理所述，刚体跟随质心的平移仅与外力系的主矢有关，由质点系相对质心的动量矩定理可知，刚体相对质心平移坐标系的运动仅与外力系对质心的主矩有关。

于是，由式(8.1.11)可写出y C x C F ym F x m R R ,==&&&& (8.1.55) 式中m 为刚体的质量，F R x , F R y 分别是外力系的主矢在y x ,方向上的分量。

由式(8.1.54)在垂直于平面图形S 方向上的投影，可得Cz CzM tL =d d (8.1.56) 其中M Cz 是外力系对通过质心且垂直于平面图形S 的轴之矩的代数和。

而ϕ&C Cz J L =，J C 是刚体对于通过质心且垂直于平面图形S 的轴的转动惯量。

应用质心运动定理和相对质心的动量矩定理，得到了三个动力学方程，给出了三个广义坐标x C , y C 和ϕ的封闭方程组，用以解决刚体的平面运动问题。

动力学方程组m (8.1.57)Cz C ni iy C n i ix C M J F ym F x ===∑∑==ϕ&&&&&&,,11称为刚体平面运动微分方程组。

给出相应的初始条件，例如，t ＝0时，刚体质心的位置分别为x C 0和y C 0，质心在初始时的速度分别为和，平面图形S 在初始时的角位移和角速度分别为ϕ0C x &0C y&0和0ϕ&。

第八章 刚体的平面运动答 案8－1均不可能。

利用速度投影定理考虑。

8－2不对。

，不是同一刚体的速度，不能这样确定速度瞬心。

8－3不对。

杆 和三角板ABC不是同一刚体，且两物体角速度不同，三角板的瞬心与干的转轴不重合。

8－4各点速度、加速度在该瞬时一定相等。

用求加速度的基点法可求出此时图形的角速度、角加速度均等于零。

8－5在图（a）中，=，= ，因为杆AB作平移；在图（b）中，=，≠，因为杆AB作瞬时平移。

8－6车轮的角加速度等于 。

可把曲面当作固定不动的曲线齿条，车轮作为齿轮，则齿轮与齿条接触处的速度和切向加速度应该相等，应有，然后取轮心点O为基点可得此结果和速度瞬心C的加速度大小和方向。

8－7由加速度的基点法公式开始，让 ω=0，则有 ，把此式沿着两点连线投影即可。

8－8可能：图b、e；不可能：图a、c、d、f、g、h、i、j、k和l。

主要依据是求加速度基点法公式，选一点为基点，求另一点的加速度，看看是否可能。

8－9（1）单取点A或B为基点求点C的速度和加速度均为三个未知量，所以应分别取A，B为基点，同时求点C的速度和加速度，转换为两个未知量求解（如图a）。

（2）取点B为基点求点C的速度和加速度，选点C为动点，动系建于杆，求点C的绝对速度与绝对加速度，由 ，转换为两个未知数求解（如图b）。

（3）分别取A，B为基点，同时求点D的速度和加速度，联立求得 ，再求 。

8－10（1）是。

把，沿AB方向与垂直于AB的方向分解，并选点B为基点，求点A的速度，可求得杆AB的角速度为 。

再以点B为基点，求点E的速度，同样把点E的速度沿AB方向与垂直于AB的方向分解，可求得杆AB的角速度为。

这样就有，然后利用线段比可得结果。

也可用一简捷方法得此结果。

选点A（或点B）为基点，则杆AB上任一点E的速度为= + ，垂直于杆AB，杆AB上各点相对于基点A的速度矢端形成一条直线，又=+ ，所以只需把此直线沿方向移动距离，就是任一点E的速度的矢端。

第8章刚体的平面运动一、选择题1．图8-1所示平面图形上A、B两点的加速度与其连线垂直且ɑA≠ɑB，则此瞬时平面图形的角速度ω、角加速度α应该是（）。

A．ω≠0，α＝0B．ω＝0，α≠0C．ω＝0，α＝0D．ω≠0，α≠0图8-1【答案】B2．图8-2所示各平面图形的速度分布为：（a）v A＝－v B，v A不垂直AB，这种速度分布是（）。

A．可能的B．不可能的不垂直AB，，这种速度分布是（）。

A．可能的B．不可能的图8-2【答案】B；B3．在图8-3所示机构中，则ω1（）ω2。

A．＝B．＞C．＜图8-3【答案】C4．在图8-4所示机构的几种运动情况下，平面运动刚体的速度瞬心为：（a）（）；（b）（）；（c）（）；（d）（）。

A．无穷远处B．B点C．A、B两点速度垂线的交点D．A点E．C点图8-4【答案】D；B；A；C5．已知图8-5所示平面图形上B点的速度v B，若以A为基点，并欲使是B点相对于A点的速度，则A点的速度v A（）。

A．与AB垂直B．沿AB方向，且由A指向BC．沿AB方向，且由B指向AD．与AB成φ角图8-5【答案】B二、填空题1．边长为L的等边三角形板在其自身平面内运动，已知B点的速度大小为，方向沿CB，A点的速度沿AC方向。

如图8-6所示，则此时三角板的角速度大小为______；C点的速度大小为______。

图8-6【答案】2．已知作平面运动的平面图形上A点的速度v A，方向如图8-7所示。

则B点所有可能速度中最小速度的大小为______，方向______。

【答案】；沿AB方向图8-73．已知作平面运动的平面图形（未画出）上某瞬时A点的速度大小为v A，方向如图8-8所示，B点的速度方位沿mn，AB＝l，则该瞬时刚体的角速度ω为______,转向为______。

【答案】；顺时针图8-8三、判断题1．作平面运动的平面图形上（瞬时平移除外），每一瞬时都存在一个速度瞬心。

（）【答案】对2．研究平面运动图形上各点的速度和加速度时，基点只能是该图形上或其延展面上的点，而不能是其他图形（刚体）上的点。

理论力学8章作业题解8-2 半径为r 的齿轮由曲柄OA 带动，沿半径为R 的固定齿轮滚动。

如曲柄OA 以匀角加速度a 绕O 轴转动，且当运动开始时，角速度00=w ，转角0=j 。

求动齿轮以中心Ａ为基点的平面运动方程。

解：图示，A 轮平面运动的转角为=A j ∠C 3AC 2=j +∠CAC 2由于弧长CC 1=CC 2，故有 ∠CAC 2=r R /j ，所以22/t rr R r r R r R A a j j j j +=+=+=A 轮平面运动方程为ïïîïïíì+=+=+=+=+=22212212)sin()()sin()()cos()(cos )(tr r R t r R r R y t r R r R x A A A a j a j a j8-6两刚体M ，N 用铰C 连结，作平面平行运动。

已知AC=BC=600mm ，在题附图所示位置s mm v s mm v B A /100,/200==，方向如图所示。

试求C 点的速度。

解：由速度投影定理得()()0==BC C BC B v v 。

则v C 必垂直于BC 连线，v C 与AC 连线的夹角为30°。

由()()AC A AC C v v = 即得：s mm v v A C /200== ，方向如题4-6附图示。

解毕。

8-9 图所示为一曲柄机构，曲柄OA 可绕O 轴转动，带动杆AC 在套管B 内滑动，套管B 及与其刚连的BD 杆又可绕通过B 铰而与图示平面垂直的水平轴运动。

已知：OA ＝BD ＝300mm ，OB ＝400mm ，当OA 转至铅直位置时，其角速度ωo ＝2rad/s ，试求D 点的速度。

C 12Aj C解 (1)平面运动方法： 由题可知：BD AC w w =确定AC 杆平面运动的速度瞬心。

套筒中AC 杆上一点速度沿套筒(为什么？)s rad IAOA IA v A AC /72.00=´==w w , s mm BD BD v AC BD D /216=´=´=w w D 点加速度如何分析？关键求AC 杆角加速度(=BD 杆角速度) 基点法，分析AC 杆上在套筒内的点(B’)：(1) tA B n A B A B a a a a ¢¢¢++=r r r r大小：× ∠ ∠ × 方位：× ∠ ∠ ∠ 再利用合成运动方法：动点：套筒内AC 杆上的点B’，动系：套筒。

第8章 刚体平面运动概述和运动分解一、是非题(正确的在括号内打“√”、错误的打“×"）1．平面图形的角速度与图形绕基点转动的角速度始终相等。

（ √ ) 2．刚体平面运动可视为随同基点的平动和绕基点转动的合成运动. （ √ ） 3．平面图形上如已知某瞬时两点的速度为零,则此平面图形的瞬时角速度和瞬时角加速度一定为零。

（ × ) 4．在某一瞬时平面图形上各点的速度大小都相等，方向都相同，则此平面图形一定作平动,因此各点的加速度也相等. （ × ) 5．车轮沿直线轨道滚而不滑，某瞬时车轮与轨道的接触点为车轮的速度瞬心，其速度为零，故速度瞬心的加速度亦为零. （ × ） 6．当0=ω时，平面图形上两点的加速度在此两点连线上的投影相等。

（ √ ) 7．平面图形在其平面内运动，某瞬时其上有两点的加速度矢相同，其上各点速度在该瞬时一定相等。

（ √ ) 二、填空题1．刚体在运动过程中，其上任一点到某一固定平面的距离保持不变，这种运动称为刚体的 平面运动。

刚体的平面运动可简化为平面图形在其自身平面内的运动。

2．平面图形的运动可分解为随基点的平动和绕基点的转动。

平动为牵连运动，它与基点的选择有关；转动为相对运动，它与基点的选择无关。

3．通常把平面运动的角速度和角加速度直接称为刚体的角速度和角加速度,而无须指明它们是对哪个基点而言。

4．平面图形上各点的加速度的方向都指向同一点，则此瞬时平面图形的角加速度等于零。

5．相对某固定平面作平面运动的刚体,则刚体上与此固定平面垂直的直线都作平动。

三、选择题1．正方平面图形在其自身平面内作平面运动。

已知四点A 、B 、C 、D 的速度大小相等,方向如图8.23（a ）、（b ）图所示，问下列结论哪个正确。

（ D )(A) (a)、(b ）图的运动都是可能的 (B) （a)、(b)图的运动都是不可能的 (C) 只有（a)图的运动是可能的（D) 只有 (b)图的运动是可能的C vADBCA vB vC vD v(a)ADBCA vB vD v(b)图8。