正交试验设计方法(详细步骤) 共67页
- 格式:ppt
- 大小:741.00 KB
- 文档页数:67







正交试验设计的流程正交试验设计是一种有效的统计方法,用于确定影响某个过程或系统的多个因素的最佳组合。
它可以帮助研究人员在有限的实验次数中获得尽可能多的信息,从而优化产品或过程的性能。
在本文中,我们将介绍正交试验设计的流程,以帮助读者更好地理解和应用这一方法。
第一步:确定实验目标和因素在进行正交试验设计之前,首先需要明确实验的目标和需要研究的因素。
实验目标可以是改进产品的性能、降低生产成本、提高工艺效率等。
因素则是影响实验结果的各种变量,例如材料的种类、温度、压力等。
在确定因素时,需要考虑到可能的相互作用效应,以确保实验结果的准确性。
第二步:选择正交表正交表是正交试验设计的基础,用于确定实验的运行次数和因素的水平。
根据实验因素的个数和水平数,可以选择合适的正交表。
常用的正交表有Taguchi L9、L12、L16等。
选择正交表时,需要考虑因素个数和水平数的平衡性,以及实验次数的可行性。
第三步:确定试验方案在确定了正交表之后,需要根据具体的实验目标和因素,确定试验方案。
试验方案包括确定实验的次数、因素的水平和实验的顺序。
通常情况下,每个因素的水平应该均匀分布在正交表的各个列中,以保证各个因素的效应能够被准确估计。
第四步:进行实验在正交试验设计中,实验次数通常是有限的,因此需要合理安排实验的顺序。
一般来说,应该先进行主要因素的实验,然后再进行次要因素的实验。
在实验过程中,需要记录每次实验的结果和观察值,以便后续的数据分析和结果解释。
第五步:数据分析和结果解释在完成实验后,需要对实验数据进行统计分析和结果解释。
常用的分析方法包括方差分析、回归分析和假设检验等。
通过分析实验数据,可以确定各个因素对实验结果的影响程度,并找出最佳的因素组合。
第六步:优化和验证根据实验结果,可以进行产品或过程的优化。
通过调整因素的水平和组合,可以进一步改进产品的性能或降低生产成本。
此外,还需要进行实验结果的验证,以确保实验结果的可靠性和稳定性。

正交试验设计流程
正交试验设计流程:
①明确试验目的:确定试验要解决的问题,明确希望通过试验达到的目标,比如优化产品性能、提高生产效率等。
②选择影响因素:基于理论分析和经验判断,识别可能影响试验结果的主要因素,如温度、压力、材料种类等。
③确定因素水平:为每个影响因素设定几个不同的水平,水平的选择应覆盖该因素的预期变化范围。
④选取正交表:根据试验因素的数量和每个因素的水平数,选择合适的正交表,确保试验设计的均衡性和代表性。
⑤编制试验方案:根据选定的正交表,编制具体的试验方案,列出每组试验的具体条件组合。
⑥进行试验:按照试验方案进行试验,记录每一组试验的结果,确保试验过程中的操作一致性和准确性。
⑦数据整理:将试验结果进行整理,通常以表格形式呈现,便于后续的数据分析。
⑧数据分析:运用统计学方法分析试验数据,计算各因素对结果的影响程度,找出最优组合。
⑨结果解释:解读数据分析结果,明确哪些因素是关键影响因素,哪些水平组合能产生最佳效果。
⑩验证试验:为了确认试验结果的可靠性,可以进行验证试验,重复最优组合的试验条件,看是否能稳定得到相同或相似的结果。
⑪优化方案:基于正交试验的结果,提出优化产品或工艺的方案,可能包括参数调整、工艺改进等。
⑫实施与跟踪:将优化方案应用于实际生产中,跟踪实施效果,确保达到预期的优化目标。
⑬文档记录:详细记录整个正交试验设计的过程、结果和结论,为后续的研究和生产提供参考。


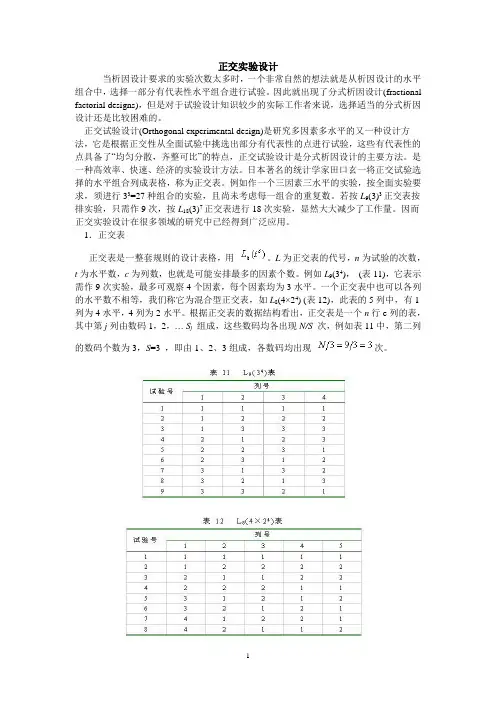
正交实验设计当析因设计要求的实验次数太多时,一个非常自然的想法就是从析因设计的水平组合中,选择一部分有代表性水平组合进行试验。
因此就出现了分式析因设计(fractional factorial designs),但是对于试验设计知识较少的实际工作者来说,选择适当的分式析因设计还是比较困难的。
正交试验设计(Orthogonal experimental design)是研究多因素多水平的又一种设计方法,它是根据正交性从全面试验中挑选出部分有代表性的点进行试验,这些有代表性的点具备了“均匀分散,齐整可比”的特点,正交试验设计是分式析因设计的主要方法。
是一种高效率、快速、经济的实验设计方法。
日本著名的统计学家田口玄一将正交试验选择的水平组合列成表格,称为正交表。
例如作一个三因素三水平的实验,按全面实验要求,须进行33=27种组合的实验,且尚未考虑每一组合的重复数。
若按L9(3)3正交表按排实验,只需作9次,按L18(3)7正交表进行18次实验,显然大大减少了工作量。
因而正交实验设计在很多领域的研究中已经得到广泛应用。
1.正交表正交表是一整套规则的设计表格,用。
L为正交表的代号,n为试验的次数,t为水平数,c为列数,也就是可能安排最多的因素个数。
例如L9(34),(表11),它表示需作9次实验,最多可观察4个因素,每个因素均为3水平。
一个正交表中也可以各列的水平数不相等,我们称它为混合型正交表,如L8(4×24) (表12),此表的5列中,有1列为4水平,4列为2水平。
根据正交表的数据结构看出,正交表是一个n行c列的表,其中第j列由数码1,2,… S j组成,这些数码均各出现N/S次,例如表11中,第二列的数码个数为3,S=3 ,即由1、2、3组成,各数码均出现次。
正交表具有以下两项性质:(1)每一列中,不同的数字出现的次数相等。
例如在两水平正交表中,任何一列都有数码“1”与“2”,且任何一列中它们出现的次数是相等的;如在三水平正交表中,任何一列都有“1”、“2”、“3”,且在任一列的出现数均相等。
正交实验的设计方案正交实验是一种用于确定影响因素对实验结果影响的统计方法。
它可以帮助研究人员以少量实验设计来获取全面可靠的数据,从而进行合理的判断和决策。
正交实验的设计方案是一项关键工作,本文将讨论如何进行正交实验的设计方案,并提供一个实际案例。
一、正交实验的基本原理正交实验基于统计学的原理,通过一系列的实验来确定各个因素对结果的影响程度,并找出最优的组合方式。
正交实验中,要考虑的因素被称为水平或处理水平,这些水平可以是定性的(如颜色、形状等),也可以是定量的(如温度、压力等)。
关键是选择合适的水平组合,以获得准确、全面的数据。
二、正交实验的设计方法1. 确定因素和水平:首先确定需要考虑的因素及其对应的水平。
根据实际情况和研究目的,选择合适的因素和水平,保证实验结果的可靠性和可解释性。
2. 构建正交表:利用正交表是进行正交实验设计的核心步骤。
正交表将各个水平组合按照一定的规律排列,确保每个水平在实验中均匀分布,并减少误差的影响。
常用的正交表包括拉丁方、矩形方和正交平方等。
3. 进行实验:根据正交表的设计,进行实验。
确保实验过程的准确性和可重复性,记录实验数据。
4. 分析实验数据:通过统计学方法对实验数据进行分析,评估各个因素对结果的影响程度。
常用的分析方法包括方差分析、回归分析和卡方检验等。
5. 优化方案选择:根据实验结果,确定最优的因素组合和水平选择。
同时,可以进一步优化实验方案,提高研究效果和实验效率。
三、实际案例以某电子产品的设计为例,我们需要确定屏幕亮度、音量大小和屏幕分辨率对用户体验的影响程度。
我们选择了三个水平来表示这三个因素,分别是:低、中、高。
通过正交实验的设计方案,我们利用正交表构建了以下实验方案:因素1:屏幕亮度(低、中、高)因素2:音量大小(低、中、高)因素3:屏幕分辨率(低、中、高)在表中,每一行代表一个实验条件,我们总共需要进行9次实验。
实验数据如下:实验结果屏幕亮度音量大小屏幕分辨率实验1 低低低实验2 低中中实验3 低高高实验4 中低中实验5 中中高实验6 中高低实验7 高低高实验8 高中低实验9 高高中通过对实验数据的统计分析,我们可以得出每个因素对用户体验的影响程度。
正交试验设计步骤-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN正交试验设计步骤1 在SPSS中手动录入数据。
请注意写入空白列。
2 点击数据→正交设计→生成,出现“生成正交设计”对话框。
按因素水平表进行赋值,空白列的赋值为1“1”,2“2”,3“3”3 点击“数据”→“正交设计”→“显示”,空白列的D可不加到右边的“因子”框中。
4 测量数据填入表8中的“STATUS_”列的相应单元格中5单击“分析”→“一般线性模型”→“单变量”注意不要选“空白列”6 单击“对比”→选择“简单”7 单击“模型”→选择“设定”→将“A”、“B”、“C”选入右边的“模型”中→单击“构建项”中的“主效应”,8 单击“选项”→将“因子与因子交互”中的“A”、“B”、“C”选入“显示均值”中→勾选“比较主效应”,9 结果分析(1)方差分析结果主体间因子值标签N硬脂酸钠溶液浓度1403根据正交试验方差分析可知,硬脂酸钠溶液浓度和硫酸铝溶液浓度对试验指标的影响非常显著,而处理时间对试验指标的影响不显著。
影响程度的大小也有差异,A>B(2)单因素统计量分析1. 硬脂酸钠溶液浓度成对比较因变量:STATUS_差异。
综合上述两表可以得出:B3均数最大(),且B1与B2、B3之间存在显著性的差异,B2、B3之间不存在显著性的差异。
3.浸渍时间估计综合上述两表可以得出:C1均数最大(),C1、C2、C3之间不存在显著性的差异。
(3)结论涤纶防水整理的较佳工艺条件是A3B3C1,即硬脂酸钠溶液浓度60g/L,硫酸铝溶液浓度60g/L,处理时间5min。