斯勒茨基方程

斯勒茨基方程消费者在商品选择时如何对商品价格的变动做出反应1.替代效应和收入效应替代效应：由于两种商品之间的交换比率的变化引起的需求变化收入效应：由于购买力提高引起的需求变化①相对价格发生变动，此时调整货币收入使购买力保持不变②对购买力进行调整，同时使相对价格保持不变①预算线绕原需求束转动②平移①具有相同的斜率（具有相同的相对价格），纵截距不同（货币收入不同），购买力保持不变②相对价格保持不变，收入变动m ′ = p 1 ′ x 1 + p 2 x 2 m'=p_1'x_1+p_2x_2 m′=p1′x1+p2 x2m = p 1 x 1 + p 2 x 2 m=p_1x_1+p_2x_2 m=p1x1+p2x2⇒ m ′ − m = x 1 [ p 1 ′ − p 1 ] \Rightarrow m'-m=x_1[p_1'-p_1] ⇒m′−m=x1[p1′−p1]Δ m = x 1 Δ p 1 \Delta m =x_1\Delta p_1 Δm=x1Δp1。

原来的预算线最佳选择为X转动后的预算线最佳选择为Y移动后的预算线最佳选择为Z从X到Y的移动就称为替代效应替代效应Δ x 1 s = x 1 ( p 1 ′ , m ′ ) − x 1 ( p 1 , m ) \Delta x_1^s=x_1(p_1',m')-x_1(p_1,m) Δx1s=x1(p1′,m′)−x1(p1,m)。

从Y到Z的移动就称为收入效应收入效应Δ x 1 n = x 1 ( p 1 ′ , m ) − x 1 ( p 1 ′ , m ′ )\Delta x_1^n=x_1(p_1',m)-x_1(p_1',m') Δx1n=x1(p1′,m)−x1(p1′,m′)。

替代效应也称作补偿的需求变动收入效应既可以增加商品的需求，也可以减少商品的需求ex：计算替代效应、计算收入效应2.替代效应的符号如果p 1 > p 1 ′ p_1>p_1' p1>p1′，一定有Δ x 1 s ≥ 0 \Delta x_1^s \ge 0 Δx1s≥0替代效应总是与价格的变动相反，替代效应总是负的证明：显示偏好原理。

CH 8 斯勒茨基方程价格变化，引起的需求变化，可分解成“替代效应”、“收入效应”。

111s n x x x =+11111(',')(,)s x x p m x p m ∆=- 11111(',)(',')m x x p m x p m ∆=-※ 一、替代效应(substitution effect)1．替代效应：购买力不变，相对价格变化→需求变化。

11111(',')(,)s x x p m x p m ∆=-2．替代效应的符号：除完全互补偏好，“负”（包括凹偏好） = 替代效应引起的需求变动与价格变动反向。

3．例子？：已知：牛奶主每周生产牛奶40夸脱，最初收入=120美元，p 1=3。

牛奶的需求函数：。

问：（1）求牛奶的需求。

（2）牛奶价格变为2美元，需求？（3）牛奶价格变为2美元，维持牛奶需求量14，货币收入？ （4）替代效应？ 解：（1）收入=120美元，牛奶主对牛奶需求：x1＝14，（2）收入=120美元，需求＝16。

（3）⊿m=x1⊿p1=14（2-3）=-14 ∴m ’= m+⊿m=120-14=106 （4）x1（p ’1 ，m ’） =15.3替代效应= x （2，106）- x （3，120）= 15.3 - 14=1.3二、收入效应(income effect)1．收入效应：新相对价格不变，实际购买力/实际收入变化→需求量变化。

11111(',)(',')m x x p m x p m ∆=-2．收入效应的符号正常商品：收入效应为负—— 价格与收入反向，收入与需求量同向——价格与需求量反向。

低档商品：收入效应为正—— 价格与收入反向，收入与需求量反向——价格与需求量同向。

3、例子：如上例0.7。

三、正常、※1、正常商品价格变动效应：111s nx x x =+(-) (-) (-)正常商品，需求总变动——负——价格与需求反向——正常方向。

斯勒茨基方程是由奥地利物理学家恩斯特·斯勒茨基于1918年提出的一种描述非相对论性量子力学的波函数振荡的方程。

它是描述微观粒子（如电子）在周期性势场中的运动情况的重要方程。

斯勒茨基方程在固体物理学、半导体物理学以及纳米科学等领域有着广泛的应用，对于理解和研究结晶材料和纳米材料的电子结构以及激子的形成和传输等现象具有重要意义。

斯勒茨基方程的基本形式可以表示为：\[ -\frac{{\hbar^2}}{{2m}}\nabla^2\psi(\mathbf{r}) +V(\mathbf{r})\psi(\mathbf{r}) = E\psi(\mathbf{r})\]其中，\(\hbar\)代表约化普朗克常数，m为粒子的质量，\(\psi(\mathbf{r})\)为波函数，V(\(\mathbf{r})\)为势能函数，E为粒子的总能量。

斯勒茨基方程的形式非常简洁，但其物理意义非常丰富。

它可以用来描述粒子在势能场中的行为，例如电子在晶格中的运动。

斯勒茨基方程的解可以给出电子的波函数，从而揭示了电子在晶体中的运动方式和能级分布情况。

在固体物理学中，斯勒茨基方程被广泛运用于解释晶体的能带结构以及导电性质，对于研究材料的电子输运性质有着重要的意义。

斯勒茨基方程还可以用于描述半导体中的电子-空穴对的结合态——激子。

激子是电子和正电子在外加电场作用下形成的束缚态，它在半导体光电器件中起着重要作用。

通过对斯勒茨基方程的研究，人们可以更深入地理解激子的形成机制、能级结构以及其在半导体材料中的输运特性。

从个人的理解来看，斯勒茨基方程是描述微观粒子在势场中运动的一种重要方式。

通过对斯勒茨基方程的深入研究和解析，我们可以揭示出物质中微观粒子的行为规律，从而为材料科学和纳米科学领域的研究提供理论基础。

斯勒茨基方程的深入理解不仅可以帮助我们更好地理解材料的电子结构和能带特性，还可以为半导体光电器件的设计和性能优化提供重要指导。

斯勒茨基方程名词解释
斯勒茨基方程（Schlögl equation）是一种描述化学反应动力学的微分方程模型。

该方程由奥地利化学家Kurt Schlögl在20世纪70年代提出，用于描述复杂的化学反应网络系统。

斯勒茨基方程可以用来描述反应物浓度随时间的变化。

一般而言，它适用于描述具有多个中间物种和多个反应路径的反应网络系统。

该方程的一般形式如下：
d[Ci]/dt = ki ∏(Cj^mj) li Ci.
其中，[Ci]表示第i个物种的浓度，t表示时间，ki和li分别表示与第i个物种相关的生成速率常数和消耗速率常数。

∏(Cj^mj)表示对所有与第i个物种有关的物种j进行乘积运算，mj表示与第i个物种相关的物种j的反应阶数。

斯勒茨基方程的特点是可以描述非线性反应动力学，包括正反应速率的非线性关系、反应物浓度的相互作用以及反应网络中的正反馈和负反馈等。

该方程的求解可以通过数值方法进行，以模拟和预测化学反应系统的动力学行为。

斯勒茨基方程在化学动力学研究中具有重要的应用价值，尤其适用于描述复杂的反应网络系统，如化学反应链、催化反应和生物化学反应等。

通过对斯勒茨基方程的研究和求解，可以深入理解反应动力学的基本原理，揭示反应网络的复杂行为，并为合理设计和优化化学反应过程提供理论指导。

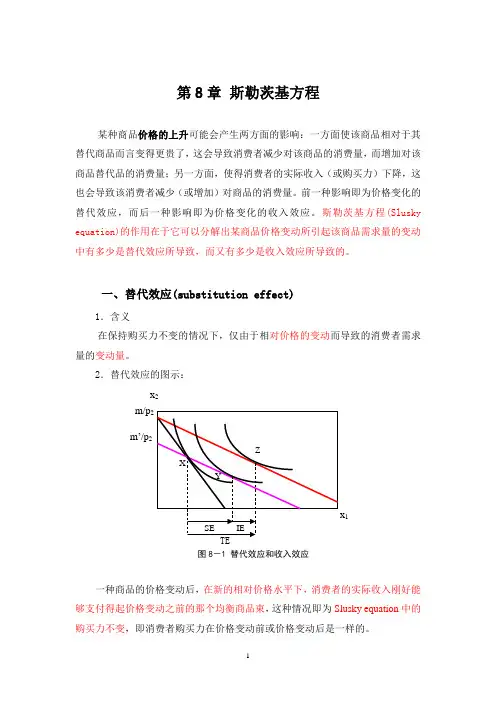
第8章斯勒茨基方程某种商品价格的上升可能会产生两方面的影响：一方面使该商品相对于其替代商品而言变得更贵了，这会导致消费者减少对该商品的消费量，而增加对该商品替代品的消费量；另一方面，使得消费者的实际收入（或购买力）下降，这也会导致该消费者减少（或增加）对商品的消费量。

前一种影响即为价格变化的替代效应，而后一种影响即为价格变化的收入效应。

斯勒茨基方程(Slusky equation)的作用在于它可以分解出某商品价格变动所引起该商品需求量的变动中有多少是替代效应所导致，而又有多少是收入效应所导致的。

一、替代效应(substitution effect)1．含义在保持购买力不变的情况下，仅由于相对价格的变动而导致的消费者需求量的变动量。

2．替代效应的图示：x2m/pm’/p2x1图8－1 替代效应和收入效应一种商品的价格变动后，在新的相对价格水平下，消费者的实际收入刚好能够支付得起价格变动之前的那个均衡商品束，这种情况即为Slusky equation中的购买力不变，即消费者购买力在价格变动前或价格变动后是一样的。

3．替代效应的计算：（1）调整货币收入以保持实际购买力不变初始均衡点：价格水平为),(21p p ，均衡商品束为),(21x x ，支付的货币为: 2211x p x p m +=（8.1）价格变动后：价格水平为),(2'1p p ，均衡商品束为)','(21x x要使消费者购买力保持不变，则货币收入应该调整为： 2111''x p x p m +=（8.2） 则在价格变动后要保持消费者购买力不变，货币收入的调整量应为式（8.1）－式（8.2）：⊿1111)'('x p p x m m m =-=-=⊿1p （8.3）（2）计算替代效应⊿),,()',,'(2112111m p p x m p p x x s -= （8.4）二、收入效应(income effect)1．含义 在新的相对价格水平下（21'p p ），仅仅由于实际购买力（或实际收入）的变化而导致的消费者需求量的变动量。

斯勒茨基方程一、斯勒茨基方程要解决的问题研究斯勒茨基方程主要目的是要解决两个问题：一是将价格变化的总效应分解为两部分，即替代效应和收入效应。

二是要解决希克斯替代效应（或希克斯需求）的不可度量问题。

解决不可度量问题也有两种方法：第一种方法是用斯勒斯基替代效应替代希克斯效应；第二种方法是通过马歇尔需求来求希克斯需求，这就是方程要解决的问题。

其表明希克斯替代效应（或者希克斯需求）等于马歇尔需求减去收入效应。

二、斯勒茨基方程的推导——方法一即根据斯勒斯基需求和希克斯需求的定义，可以直接利用微分方法得出方程的解：1．根据斯勒斯基需求的定义推导方程 假设原价格为),(21p p 时的需求为),(21x x ，故2211x p x p m +=。

当新价格为),(21p p 时，使得原消费束),(21x x 仍然支付得起的需求即为斯勒斯基需求，表示为),,,(21211x x p p x s ，这时使得原消费束支付得起的收入为：2211x p x p m +=。

根据斯勒斯基需求的定义有如下恒等式：),,(),,,(221121121211x p x p x x x x x p p x s +≡由于二者的购买力相同，即2211x p x p +的购买力与2211X p X p +的购买力相同，所以从购买角度看可以将上式写成：),,(),,,(21121211m p p x x x p p x s ≡。

对其求关于1p 的微分可以得到：1211121112111211121211),,(),,(),,(),,(),,,(x m m p p x p m p p x p m m m p p x p m p p x p x x p p x s ⋅∂∂+∂∂=∂∂⋅∂∂+∂∂=∂∂ 移项后得到：12111212111211),,(),,,(),,(x mm p p x p x x p p x p m p p x s ⋅∂∂-∂∂=∂∂ 总效应 替代效应 收入效应（马歇尔需求） （斯勒茨基需求）2．根据希克斯需求定义推导方程：希克斯需求是指在新价格条件下，维持原有效用水平不变时的需求。