最大流问题的增广路算法概要
- 格式:ppt
- 大小:160.00 KB
- 文档页数:31

最大流问题的求解方法及应用
最大流问题,是指在一个有向图中,从源点 s 到汇点 t 的最大
流量。
在实际应用中,最大流问题往往用于描述网络传输、油管输送等流量分配问题。
求解最大流问题的方法包括以下几种:
1. 网络流算法:这是一种基于图论和线性规划的算法。
通过构建网络流图,将最大流问题转化为最小割问题,再利用线性规划求解最小割问题的对偶问题来求解最大流问题。
2. 增广路算法:这是一种经典的最大流算法,其基本思想是不断找到增广路径,即从源点 s 到汇点 t 的一条路径,沿途边权
均有剩余容量,使得该路径上的边的剩余容量中的最小值最大化,最终得到最大流。
3. 矩阵树定理:这是一种基于图论和矩阵运算的算法,适用于有向图和无向图。
通过计算图的拉普拉斯矩阵的行列式等方法,求得图的生成树个数,从而计算最大流。
4. Dinic算法:是对增广路算法的改进。
在增广路算法中,每
次查找增广路径的过程需要遍历整个图,为了提高效率,
Dinic算法引入了分层图的概念,将图分层之后只在图的一层
中查找增广路径,最终求得最大流。
这些方法在实际应用中常常被用来解决路由选择、网络流量优化、模拟电路分析等问题。
例如,最大流可以被用来优化数据传输、流水线设计、流量管道的运营和管理,提高资源利用率和数据传输速度。

最大流问题解题步骤一、什么是最大流问题?最大流问题是指在一个有向图中,给定源点和汇点,每条边都有一个容量限制,求从源点到汇点的最大流量。
该问题可以用于网络传输、电力调度等实际应用中。
二、最大流问题的解法1. 增广路算法增广路算法是最基本的解决最大流问题的方法。
其基本思想是不断地寻找增广路,并将其上的流量加入到原来的流中,直到不存在增广路为止。
具体步骤如下:(1)初始化网络中各边上的流量均为0;(2)在残留网络中寻找增广路;(3)如果存在增广路,则将其上的最小剩余容量作为增量加入到原来的流中;(4)重复步骤2和步骤3,直到不存在增广路。
2. Dinic算法Dinic算法是一种改进型的增广路算法,其核心思想是通过层次分析和分层图来减少搜索次数,进而提高效率。
具体步骤如下:(1)构建分层图;(2)在分层图上进行BFS搜索寻找增广路径;(3)计算路径上可行流量并更新残留网络;(4)重复步骤2和步骤3,直到不存在增广路。
3. Ford-Fulkerson算法Ford-Fulkerson算法是一种基于增广路的算法,其核心思想是不断地寻找增广路,并将其上的流量加入到原来的流中,直到不存在增广路为止。
具体步骤如下:(1)初始化网络中各边上的流量均为0;(2)在残留网络中寻找增广路;(3)如果存在增广路,则将其上的最小剩余容量作为增量加入到原来的流中;(4)重复步骤2和步骤3,直到不存在增广路。
三、最大流问题解题步骤1. 确定源点和汇点首先需要确定问题中的源点和汇点,这是解决最大流问题的前提条件。
2. 构建残留网络在有向图中,每条边都有一个容量限制。
我们可以将这些边看作管道,容量看作管道的宽度。
在实际传输过程中,某些管道可能已经被占用了一部分宽度。
因此,在求解最大流问题时,需要构建一个残留网络来表示哪些管道还能够继续传输数据。
具体方法是:对于每条边(u,v),分别构造两条边(u,v)和(v,u),容量分别为c(u,v)-f(u,v)和f(u,v),其中c(u,v)表示边的容量,f(u,v)表示当前流量。


网络最大流的算法网络最大流的算法分类:一、Ford-Fulkerson增广路方法1、Ford-Fulkerson标号算法(最简单的实现)分别记录这一轮扩展过程中的每个点的前驱与到该节点的增广最大流量,从源点开始扩展,每次选择一个点(必须保证已经扩展到这个点),检查与它连接的所有边,并进行扩展,直到扩展到t。
2、最大容量增广路算法每次找一条容量最大的增广路来增广,找的过程类似Dijkstra,实现起来相当简单。
3、Edmonds-Karp,最短路增广算法的BFS实现每次找一条最短的增广路,BFS是一个可以很方便的实现思想。
4、距离标号算法最短路增广的O(n)寻找实现,使用距离函数d:d[t]=0;d<=d[j]+1若存在(i,j)∈E;只有路径上满足d=d[i+1]+1的增广路才为满足要求的,一开始我们初始化使标号恰好满足要求,之后不断更改标号使其可以使增广继续。
5、Dinic,分层思想对网络分层(按照距t的距离),保留相邻层之间的边,然后运用一次类似于距离标号的方法(其实质是DFS)进行增广。
二、预留与推进算法1、一般性算法随便找个点,要么将他的盈余推出去,要么对他进行重标记,直至无活跃点为止。
2、重标记与前移算法维护一个队列,对一个点不断进行推进与重标记操作,直至其盈余为0,若过程中他没有被重标记过,则可出列,否则加入队头,继续等待检查。
3、最高标号预留与推进算法记录d值,然后优先处理d值较高的,直至没有盈余。
网络最大流的算法实现一、Edmonds-Karp(EK)算法就是用广度优先搜索来实现Ford-Fulkerson方法中对增广路径的计算,时间复杂度为O(VE2),Shortest Augmenting Path (SAP) 是每次寻找最短增广路的一类算法,Edmonds - Karp 算法以及后来著名的Dinic 算法都属于此。
SAP 类算法可统一描述如下:Shortest Augmenting Path{ x <-- 0while 在残量网络Gx 中存在增广路s ~> t do{ 找一条最短的增广路径Pdelta <-- min{rij:(i,j) 属于P}沿P 增广delta 大小的流量更新残量网络Gx}return x}在无权边的有向图中寻找最短路,最简单的方法就是广度优先搜索(BFS),E-K 算法就直接来源于此。
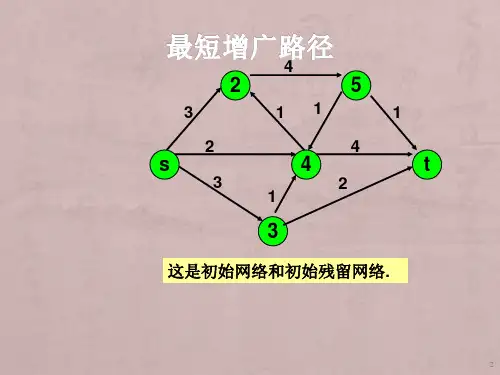

⽹络流(⼆)最⼤流的增⼴路算法传送门:⽹络流的相关定义:源点:有n个点,有m条有向边,有⼀个点很特殊,只出不进,叫做源点。
汇点:另⼀个点也很特殊,只进不出,叫做汇点。
容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常⽤c[i,j]表⽰,流量则通常是f[i,j].通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最⼤的车流量。
很显然的,流量<=容量。
⽽对于每个不是源点和汇点的点来说,可以类⽐的想象成没有存储功能的货物的中转站,所有“进⼊”他们的流量和等于所有从他本⾝“出去”的流量。
最⼤流:把源点⽐作⼯⼚的话,问题就是求从⼯⼚最⼤可以发出多少货物,是不⾄于超过道路的容量限制,也就是,最⼤流。
求解思路:⾸先,假如所有边上的流量都没有超过容量(不⼤于容量),那么就把这⼀组流量,或者说,这个流,称为⼀个可⾏流。
⼀个最简单的例⼦就是,零流,即所有的流量都是0的流。
(1).我们就从这个零流开始考虑,假如有这么⼀条路,这条路从源点开始⼀直⼀段⼀段的连到了汇点,并且,这条路上的每⼀段都满⾜流量<容量,注意,是严格的<,⽽不是<=。
(2).那么,我们⼀定能找到这条路上的每⼀段的(容量-流量)的值当中的最⼩值delta。
我们把这条路上每⼀段的流量都加上这个delta,⼀定可以保证这个流依然是可⾏流,这是显然的。
(3).这样我们就得到了⼀个更⼤的流,他的流量是之前的流量+delta,⽽这条路就叫做增⼴路。
我们不断地从起点开始寻找增⼴路,每次都对其进⾏增⼴,直到源点和汇点不连通,也就是找不到增⼴路为⽌。
(4).当找不到增⼴路的时候,当前的流量就是最⼤流,这个结论⾮常重要。
补充:(1).寻找增⼴路的时候我们可以简单的从源点开始做BFS,并不断修改这条路上的delta 量,直到找到源点或者找不到增⼴路。
(2).在程序实现的时候,我们通常只是⽤⼀个c 数组来记录容量,⽽不记录流量,当流量+delta 的时候,我们可以通过容量-delta 来实现,以⽅便程序的实现。

求解最大流问题的算法和模型最大流问题是图论中的一个基本问题,涉及到网络流的计算和优化。
在实际应用中,最大流问题的求解涉及到诸多算法和模型,如增广路径算法、Ford-Fulkerson算法、Dinic算法、最小割定理等。
本文将从这些方面进行论述。
1. 增广路径算法增广路径算法是求解最大流问题的经典算法,其基本思想是不断地寻找增广路径,通过增加路径上的流量来增加整个网络的流量。
具体来说,首先通过深度优先搜索或广度优先搜索找到一条从源点到汇点的增广路径,然后确定路径上的最小流量d,将当前流量增加d,将反向边的流量减少d,同时计算当前网络的流量。
2. Ford-Fulkerson算法Ford-Fulkerson算法是一种经典的增广路径算法,其基本理念与增广路径算法相同,但采用不同的策略来确定增广路径。
具体来说,Ford-Fulkerson算法采用贪心策略,在每次迭代中选择路径上的最小容量,从而确定增加的流量。
此外,Ford-Fulkerson算法还引入了残量图的概念,用于计算增广路径的容量。
3. Dinic算法Dinic算法是一种高效的增广路径算法,其主要优点是采用了分层图的策略来确定增广路径,使得每次迭代的搜索范围大为缩小。
具体来说,Dinic算法首先利用BFS算法确定每个节点的分层,然后在分层图上通过DFS算法查找增广路径,在路径上增加流量,更新分层图,重复此过程直至求解最大流。
4. 最小割定理最小割定理是求解最大流问题的重要定理,其核心思想是将网络分成两个不相交部分,并将其最小的割称为最小割。
最小割定理指出,在任意网络中,最大流等于最小割。
因此,求解最大流可以转化为求最小割问题,即在网络中寻找一组最小割,使得所有的割中容量最小的一组割。
总之,求解最大流问题是图论中的一个重要问题,其求解涉及到诸多算法和模型,如增广路径算法、Ford-Fulkerson算法、Dinic 算法、最小割定理等。
在实际应用中,不同情况下可能需要采用不同的算法和模型来求解,需要灵活应用。


三种⽹络流(最⼤流)的实现算法讲解与代码[洛⾕P3376题解]⽹络流(最⼤流)的实现算法讲解与代码定义对于给定的⼀个⽹络,有向图中每个的边权表⽰可以通过的最⼤流量。
假设出发点S⽔流⽆限⼤,求⽔流到终点T后的最⼤流量。
起点我们⼀般称为源点,终点⼀般称为汇点内容前置1.增⼴路在⼀个⽹络从源点S到汇点T的⼀条各边剩余流量都⼤于0(还能让⽔流通过,没有堵住)的⼀条路。
2.分层预处理出源点到每个点的距离(每次寻找增⼴路都要,因为以前原本能⾛的路可能因为⽔灌满了,导致不能⾛了).作⽤是保证只往更远的地⽅放⽔,避免兜圈⼦或者是没事就⾛回头路(正所谓⼈往⾼处⾛⽔往低处流).3.当前弧优化每次增⼴⼀条路后可以看做“榨⼲”了这条路,既然榨⼲了就没有再增⼴的可能了。
但如果每次都扫描这些“枯萎的”边是很浪费时间的。
那我们就记录⼀下“榨取”到那条边了,然后下⼀次直接从这条边开始增⼴,就可以节省⼤量的时间。
这就是当前弧优化具体怎么实现呢,先把链式前向星的head数组复制⼀份,存进cur数组,然后在cur数组中每次记录“榨取”到哪条边了。
[#3 引⽤⾃]()解决算法Ford-Fulkerson 算法(以下简称FF算法)FF算法的核⼼是找增⼴路,直到找不到为⽌。
(就是⼀个搜索,⽤尽可能多的⽔流填充每⼀个点,直到没有⽔⽤来填充,或者没有多余的节点让⽔流出去)。
但是这样的⽅法有点基于贪⼼的算法,找到反例是显⽽易见的,不⼀定可以得到正解。
为了解决这种问题,我们需要⼀个可以吃后悔药的⽅法——加反向边。
原本我们的DFS是⼀条路⾛到⿊的,现在我们每次进⼊⼀个节点,把⽔流送进去,同时建⽴⼀个权值与我们送⼊的⽔流量相等,但是⽅向相反的路(挖⼀条路让⽔流能够反向流回来,相当于给⽔流吃⼀颗后悔药)。
我们给了FF算法⼀颗后悔药之后就可以让他能够找到正确的最⼤流。
Ford-Fulkerson算法的复杂度为O(e×f) ,其中 e 为边数, f为最⼤流上代码。

最大流问题算法最大流问题算法介绍最大流问题是在网络流中的一个重要问题,它是指在一个有向图中,给定一个源点和汇点,每条边都有一个容量上限,求从源点到汇点的最大流量。
最大流问题有很多应用,如交通网络、电力系统、通信网络等。
本文将介绍最大流问题的算法。
Ford-Fulkerson算法Ford-Fulkerson算法是最早提出的解决最大流问题的方法之一。
该算法通过不断地增广路径来寻找增广路,并更新残留网络中的边权值。
具体步骤如下:1. 初始化残留网络:对于原图G(V, E),构造残留网络Gf(V, Ef),其中Ef包含所有满足c(u, v)>0或f(u, v)>0的(u, v)。
2. 寻找增广路:在残留网络中寻找从源点s到汇点t的增广路。
3. 更新残留网络:根据增广路更新残留网络中的边权值。
4. 重复步骤2和3直到不存在增广路为止。
该算法存在多种实现方式,如DFS、BFS等。
Edmonds-Karp算法Edmonds-Karp算法是Ford-Fulkerson算法的一种特殊实现方式,使用BFS来寻找增广路。
该算法的时间复杂度为O(VE^2),其中V和E分别为原图G(V, E)的顶点数和边数。
Dinic算法Dinic算法是一种基于分层图的最大流算法,它通过构造分层图来寻找增广路。
该算法的时间复杂度为O(V^2E),其中V和E分别为原图G(V, E)的顶点数和边数。
Push-Relabel算法Push-Relabel算法是一种基于预流推进的最大流算法,它通过不断地调整节点之间的流量来求解最大流。
该算法存在多种实现方式,如FIFO、HL等。
其中HL算法是一种比较优秀的实现方式,它将节点按照高度进行划分,并使用桶来管理节点。
总结以上介绍了最大流问题的四种常见算法:Ford-Fulkerson、Edmonds-Karp、Dinic和Push-Relabel。
这些算法各有优缺点,在实际应用中需要根据具体情况选择合适的算法。
求解最大流问题的增广链算法支天红【摘要】在剩余网络的基础上定义增广链,进而顺理成章地得出结论"可行流是最大流的充要条件是不存在关于该流的增广链"。
这种方法直观形象,易于理解,便于操作。
避免了用非饱和边和非零流边定义增广链给学生造成的理解困难。
【期刊名称】《林区教学》【年(卷),期】2012(000)002【总页数】2页(P74-75)【关键词】运筹学;最大流问题;剩余网络;增广链【作者】支天红【作者单位】哈尔滨铁道职业技术学院数理化教研部,哈尔滨150081【正文语种】中文【中图分类】O233许多系统中包含着流量问题。
例如,交通系统中有车辆流,控制系统中有信息流,供水系统中有水流,金融系统中有现金流等。
最大流问题考虑的是怎样使通过某一网络的流量达到最大。
可概括如下:(1)所有流经网络的流都起源于同一点,叫发点,终止于另一个点,叫收点,剩余的其他点叫中间点。
(2)流的方向由箭头标明,弧的容量就是允许的最大流量。
在发点,所有的流都从这一点发出;在收点,所有的流都指向这一点。
(3)问题的目标是使从发点到收点的总流量达到最大。
这个值可由发点的流出量或收点的流入量来衡量。
1.两个直观的概念——剩余网络和增广链(1)所谓“剩余网络”。
在一些流量被分配到弧中后,剩余网络显示了可用来额外分配的剩余的弧容量(称为剩余容量)。
例如,图1中vs→v1,它的弧容量为13,通过这条弧的流量已分配为7,则vs→v1的剩余容量为13-7=6,即可再分配给vs→v1上的流量为6。
这种状态可用图2所示的剩余网络来描述。
图2中节点旁边的数字给出了从该节点到另一节点弧的剩余容量,即说明从vs到v1的剩余容量为6。
而右边的7则表示可以抵消先前分配给vs→v1的流量。
图1给出的可行流的剩余网络如图3所示。
对于任意一个最大流问题,最初,在未分配任何流之前,其剩余网络是这样来确定的:原始网络上的每条弧都从有向弧变成了无向弧,但原来方向上的弧容量并未改变,而其相反方向上的弧容量则为零,所以原来的弧流量限制并未改变。
⽹络流之最⼤流的增⼴路径算法扩展:多路增⼴⼀般的,在执⾏增⼴路算法时,都是先⽤BFS或DFS从源到汇找到⼀条增⼴路,记录下应修改的流量,然后再顺着路倒回去增⼴.反复这个过程直到增⼴路找不到了为⽌.显然的,我们做了很多⽆⽤功,假设有两条很长的增⼴路,前⾯⼤部分都是重叠的,只是在最后关头分了个岔,⽽程序却把前⾯很长的路⾛了两次.为什么要这样?不妨把两条增⼴路合并起来,不⽌是两条,所有的增⼴路都可以按其前缀合并起来,⽽形成⼀棵增⼴树.找增⼴树可以⽤DFS,正如⽣成搜索树⼀样.简⽽⾔之,对于当前的每⼀个结点记录⼀个可提供的最⼤流量,源点的可供流量显然是⽆穷⼤,当推到下⼀个点时,最⼤流量取边的容量和上个点提供的最⼤流量的较⼩值.当到达汇点时,⾃然DFS开始回朔,这时按当前点的已⽤流量增⼴当前点与他⽗亲相连的边,同时将增⼴值累加到他⽗亲的已⽤流量上,并在他⽗亲的可提供流量上减掉这个值,以便在搜索他⽗亲剩下的⼉⼦时,让所有⼉⼦的已⽤流量总和不⼤于⽗亲的可提供流量,不然就出错了.我们按照以下步骤做:search node(available){1.得到node的可提供流量available2.search node's all son(可提供流量){inc(已⽤流量,当前⼉⼦实际增⼴的流量)dec(可提供流量,<同上>)}3.⽤得到的已⽤流量的值增⼴边(node-node's father)4.return 边的增⼴量到 node'fahter}每进⾏⼀次以上步骤,我们就完成了⼀次多路增⼴,并且返回了⼀个值到源点,即DFS的根.这个值表⽰本次操作中将流量扩⼤了多少.重复操作直到返回值为0.得到最⼤流的数值即累加每次的返回值.#include <iostream>#include <queue>#define msize 1024 //最⼤顶点数⽬using namespace std;int d[msize];//标号int r[msize][msize];//残留⽹络,初始为原图int num[msize];//num[i]表⽰标号为i的顶点数有多少int pre[msize];int n,m,s,t;//m个顶点,n条边,从源点s到汇点tvoid ini_d()//BFS计算标号,汇点t标号为0{int k;queue<int>Q;memset(d,1,sizeof(d));memset(num,0,sizeof(num));Q.push(t);d[t]=0;num[0]=1;while(!Q.empty()){k=Q.front(),Q.pop();for(int i=0;i<m;i++){if(d[i]>=m&&r[i][k]>0){d[i]=d[k]+1;Q.push(i);num[d[i]]++;}}}}int findAlowArc(int i)//从i出发寻找允许弧{int j;for(j=0;j<m;j++)if(r[i][j]>0&&d[i]==d[j]+1)return j;return-1;}int reLable(int i)//重新标号{int mm=INT_MAX;for(int j=0;j<m;j++)if(r[i][j]>0) mm=min(mm,d[j]+1);return mm==INT_MAX?m:mm;}int maxFlow(int s,int t)//从源点s出发的最⼤流{int flow=0,i=s,j;int delta;//增量memset(pre,-1,sizeof(pre));while(d[s]<m){j=findAlowArc(i);if(j>=0){pre[j]=i;i=j;if(i==t)//更新残留⽹络{delta=INT_MAX;for(i=t;i!=s;i=pre[i])delta=min(delta,r[pre[i]][i]);for(i=t;i!=s;i=pre[i])r[pre[i]][i]-= delta, r[i][pre[i]]+= delta;flow += delta;}}else{int x=reLable(i);//重新标号num[x]++;num[d[i]]–;if(num[d[i]]==0)return flow;//间隙优化d[i]=x;if(i!=s) i=pre[i];}}return flow;}FF算法分为三个步骤,⾸先寻找⼀条增⼴路(如果没有增⼴路,则返回最⼤流),同时保存路径;其次,对路径上的流量求最⼩值,记为min;最后根据路径修改⽹络,对于前向边,减去最⼩值,对于后向边,加上最⼩值,或者直接修改容量。
网络通信技术Network Communication Technology电子技术与软件工程Electronic Technology&Software Engineering 一种新的增广路径最大流算法李江龙马诗贵(遵义医科大学计算机网络管理中心贵州省遵义市563000)摘要:本文提出一种新的增广路径最大流算法,关键顶点可行分量算法(KPFC),引入关键顶点机制,将其去除,从而求出网络图的可行分量,再在可行分量中寻找增广路,从而简化路径寻找的难度,替代反向边机制,有效降低算法复杂度。
关键词:反向边;最大流;可行流;增广路;残存网络;层次网络;可行分量;关键顶点1引言“网络流理论”是在20世纪50年代由Ford-Fulkerson两人建立的,是网络应用的重要组成部分,1955年,最大流问题在铁路运输行业被首次提出,在1956年,Ford-Fulkerson又创建了最大流理论,首次提出了“最大流,最小割”的重要学说,给出了解决最大流问题的算法。
目前,最大流算法分成两大类,第一类是增广路径算法,包含Ford-Fulkerson算法⑴,Edmond-Karp121算法以及Dinic⑶算法等;第二类是预流推进算法,典型的有FIFO预流推进算法和HLLP算法等。
本文主要研究增广路径算法的改进方法。
在增广路径算法中,由于算法本身的缺陷,导致对于路径的选择存在随机性,加上我们采用了贪婪算法求解最大流,所以在开始寻找增广路径时并没有考虑到全局最优选择,即便采用了故优选择,在某些特定的情况下,仍然会造成在找到正确的最大流Z前,网络图提前失去连通性,这是一个影响算法正确性的致命问题。
为了解决问题,我们必须牺牲算法的效率,寻找通用性较高的方法,保障算法的正确性。
以往的最大流算法利用反向边思路提供•个反悔机制巴通过将错误占用的边以及流量退还,给算法…个重新选择路径的机会,选出不会导致网络图提前失去连通性的增广路径,这种方法能很好的解决上述问题,但是另•方面,算法的复杂度也由于反悔带来的多余步骤而上升。