最大流的增广路算法(KM算法).
- 格式:docx
- 大小:45.80 KB
- 文档页数:5

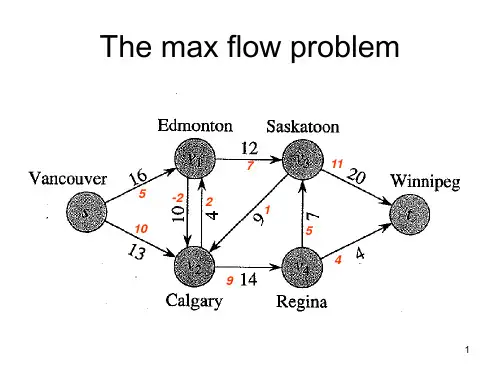
最大流问题解题步骤一、什么是最大流问题?最大流问题是指在一个有向图中,给定源点和汇点,每条边都有一个容量限制,求从源点到汇点的最大流量。
该问题可以用于网络传输、电力调度等实际应用中。
二、最大流问题的解法1. 增广路算法增广路算法是最基本的解决最大流问题的方法。
其基本思想是不断地寻找增广路,并将其上的流量加入到原来的流中,直到不存在增广路为止。
具体步骤如下:(1)初始化网络中各边上的流量均为0;(2)在残留网络中寻找增广路;(3)如果存在增广路,则将其上的最小剩余容量作为增量加入到原来的流中;(4)重复步骤2和步骤3,直到不存在增广路。
2. Dinic算法Dinic算法是一种改进型的增广路算法,其核心思想是通过层次分析和分层图来减少搜索次数,进而提高效率。
具体步骤如下:(1)构建分层图;(2)在分层图上进行BFS搜索寻找增广路径;(3)计算路径上可行流量并更新残留网络;(4)重复步骤2和步骤3,直到不存在增广路。
3. Ford-Fulkerson算法Ford-Fulkerson算法是一种基于增广路的算法,其核心思想是不断地寻找增广路,并将其上的流量加入到原来的流中,直到不存在增广路为止。
具体步骤如下:(1)初始化网络中各边上的流量均为0;(2)在残留网络中寻找增广路;(3)如果存在增广路,则将其上的最小剩余容量作为增量加入到原来的流中;(4)重复步骤2和步骤3,直到不存在增广路。
三、最大流问题解题步骤1. 确定源点和汇点首先需要确定问题中的源点和汇点,这是解决最大流问题的前提条件。
2. 构建残留网络在有向图中,每条边都有一个容量限制。
我们可以将这些边看作管道,容量看作管道的宽度。
在实际传输过程中,某些管道可能已经被占用了一部分宽度。
因此,在求解最大流问题时,需要构建一个残留网络来表示哪些管道还能够继续传输数据。
具体方法是:对于每条边(u,v),分别构造两条边(u,v)和(v,u),容量分别为c(u,v)-f(u,v)和f(u,v),其中c(u,v)表示边的容量,f(u,v)表示当前流量。

(一):用的比较多的初期:一.基本算法:(1)枚举. (poj1753,poj2965)(2)贪心(poj1328,poj2109,poj2586)(3)递归和分治法.(4)递推.(5)构造法.(poj3295)(6)模拟法.(poj1068,poj2632,poj1573,poj2993,poj2996)二.图算法:(1)图的深度优先遍历和广度优先遍历.(2)最短路径算法(dijkstra,bellman-ford,floyd,heap+dijkstra)(poj1860,poj3259,poj1062,poj2253,poj1125,poj2240)(3)最小生成树算法(prim,kruskal)(poj1789,poj2485,poj1258,poj3026)(4)拓扑排序(poj1094)(5)二分图的最大匹配(匈牙利算法) (poj3041,poj3020)(6)最大流的增广路算法(KM算法). (poj1459,poj3436)三.数据结构.(1)串(poj1035,poj3080,poj1936)(2)排序(快排、归并排(与逆序数有关)、堆排) (poj2388,poj2299)(3)简单并查集的应用.(4)哈希表和二分查找等高效查找法(数的Hash,串的Hash)(poj3349,poj3274,POJ2151,poj1840,poj2002,poj2503)(5)哈夫曼树(poj3253)(6)堆(7)trie树(静态建树、动态建树) (poj2513)四.简单搜索(1)深度优先搜索(poj2488,poj3083,poj3009,poj1321,poj2251)(2)广度优先搜索(poj3278,poj1426,poj3126,poj3087.poj3414)(3)简单搜索技巧和剪枝(poj2531,poj1416,poj2676,1129)五.动态规划(1)背包问题. (poj1837,poj1276)(2)型如下表的简单DP(可参考lrj的书page149):1.E[j]=opt{D+w(i,j)} (poj3267,poj1836,poj1260,poj2533)2.E[i,j]=opt{D[i-1,j]+xi,D[i,j-1]+yj,D[i-1][j-1]+zij} (最长公共子序列) (poj3176,poj1080,poj1159)3.C[i,j]=w[i,j]+opt{C[i,k-1]+C[k,j]}.(最优二分检索树问题)六.数学(1)组合数学:1.加法原理和乘法原理.2.排列组合.3.递推关系.(POJ3252,poj1850,poj1019,poj1942)(2)数论.1.素数与整除问题2.进制位.3.同余模运算.(poj2635, poj3292,poj1845,poj2115)(3)计算方法.1.二分法求解单调函数相关知识.(poj3273,poj3258,poj1905,poj3122)七.计算几何学.(1)几何公式.(2)叉积和点积的运用(如线段相交的判定,点到线段的距离等). (poj2031,poj1039)(3)多边型的简单算法(求面积)和相关判定(点在多边型内,多边型是否相交) (poj1408,poj1584)(4)凸包. (poj2187,poj1113)中级:一.基本算法:(1)C++的标准模版库的应用. (poj3096,poj3007)(2)较为复杂的模拟题的训练(poj3393,poj1472,poj3371,poj1027,poj2706)二.图算法:(1)差分约束系统的建立和求解. (poj1201,poj2983)(2)最小费用最大流(poj2516,poj2516,poj2195)(3)双连通分量(poj2942)(4)强连通分支及其缩点.(poj2186)(5)图的割边和割点(poj3352)(6)最小割模型、网络流规约(poj3308, )三.数据结构.(1)线段树. (poj2528,poj2828,poj2777,poj2886,poj2750)(2)静态二叉检索树. (poj2482,poj2352)(3)树状树组(poj1195,poj3321)(4)RMQ. (poj3264,poj3368)(5)并查集的高级应用. (poj1703,2492)(6)KMP算法. (poj1961,poj2406)四.搜索(1)最优化剪枝和可行性剪枝(2)搜索的技巧和优化(poj3411,poj1724)(3)记忆化搜索(poj3373,poj1691)五.动态规划(1)较为复杂的动态规划(如动态规划解特别的施行商问题等)(poj1191,poj1054,poj3280,poj2029,poj2948,poj1925,poj3034)(2)记录状态的动态规划. (POJ3254,poj2411,poj1185)(3)树型动态规划(poj2057,poj1947,poj2486,poj3140)六.数学(1)组合数学:1.容斥原理.2.抽屉原理.3.置换群与Polya定理(poj1286,poj2409,poj3270,poj1026).4.递推关系和母函数.(2)数学.1.高斯消元法(poj2947,poj1487, poj2065,poj1166,poj1222)2.概率问题. (poj3071,poj3440)3.GCD、扩展的欧几里德(中国剩余定理) (poj3101)(3)计算方法.1.0/1分数规划. (poj2976)2.三分法求解单峰(单谷)的极值.3.矩阵法(poj3150,poj3422,poj3070)4.迭代逼近(poj3301)(4)随机化算法(poj3318,poj2454)(5)杂题.(poj1870,poj3296,poj3286,poj1095)七.计算几何学.(1)坐标离散化.(2)扫描线算法(例如求矩形的面积和周长并,常和线段树或堆一起使用).(poj1765,poj1177,poj1151,poj3277,poj2280,poj3004)(3)多边形的内核(半平面交)(poj3130,poj3335)(4)几何工具的综合应用.(poj1819,poj1066,poj2043,poj3227,poj2165,poj3429)高级:一.基本算法要求:(1)代码快速写成,精简但不失风格(poj2525,poj1684,poj1421,poj1048,poj2050,poj3306)(2)保证正确性和高效性. poj3434二.图算法:(1)度限制最小生成树和第K最短路. (poj1639)(2)最短路,最小生成树,二分图,最大流问题的相关理论(主要是模型建立和求解)(poj3155, poj2112,poj1966,poj3281,poj1087,poj2289,poj3216,poj2446(3)最优比率生成树. (poj2728)(4)最小树形图(poj3164)(5)次小生成树.(6)无向图、有向图的最小环三.数据结构.(1)trie图的建立和应用. (poj2778)(2)LCA和RMQ问题(LCA(最近公共祖先问题) 有离线算法(并查集+dfs) 和在线算法(RMQ+dfs)).(poj1330)(3)双端队列和它的应用(维护一个单调的队列,常常在动态规划中起到优化状态转移的目的). (poj2823)(4)左偏树(可合并堆).(5)后缀树(非常有用的数据结构,也是赛区考题的热点).(poj3415,poj3294)四.搜索(1)较麻烦的搜索题目训练(poj1069,poj3322,poj1475,poj1924,poj2049,poj3426)(2)广搜的状态优化:利用M进制数存储状态、转化为串用hash表判重、按位压缩存储状态、双向广搜、A*算法. (poj1768,poj1184,poj1872,poj1324,poj2046,poj1482)(3)深搜的优化:尽量用位运算、一定要加剪枝、函数参数尽可能少、层数不易过大、可以考虑双向搜索或者是轮换搜索、IDA*算法. (poj3131,poj2870,poj2286)五.动态规划(1)需要用数据结构优化的动态规划.(poj2754,poj3378,poj3017)(2)四边形不等式理论.(3)较难的状态DP(poj3133)六.数学(1)组合数学.1.MoBius反演(poj2888,poj2154)2.偏序关系理论.(2)博奕论.1.极大极小过程(poj3317,poj1085)2.Nim问题.七.计算几何学.(1)半平面求交(poj3384,poj2540)(2)可视图的建立(poj2966)(3)点集最小圆覆盖.(4)对踵点(poj2079)八.综合题.(poj3109,poj1478,poj1462,poj2729,poj2048,poj3336,poj3315,poj2148,poj1263)----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------以及补充Dp状态设计与方程总结1.不完全状态记录<1>青蛙过河问题<2>利用区间dp2.背包类问题<1> 0-1背包,经典问题<2>无限背包,经典问题<3>判定性背包问题<4>带附属关系的背包问题<5> + -1背包问题<6>双背包求最优值<7>构造三角形问题<8>带上下界限制的背包问题(012背包)3.线性的动态规划问题<1>积木游戏问题<2>决斗(判定性问题)<3>圆的最大多边形问题<4>统计单词个数问题<5>棋盘分割<6>日程安排问题<7>最小逼近问题(求出两数之比最接近某数/两数之和等于某数等等)<8>方块消除游戏(某区间可以连续消去求最大效益)<9>资源分配问题<10>数字三角形问题<11>漂亮的打印<12>邮局问题与构造答案<13>最高积木问题<14>两段连续和最大<15>2次幂和问题<16>N个数的最大M段子段和<17>交叉最大数问题4.判定性问题的dp(如判定整除、判定可达性等)<1>模K问题的dp<2>特殊的模K问题,求最大(最小)模K的数<3>变换数问题5.单调性优化的动态规划<1>1-SUM问题<2>2-SUM问题<3>序列划分问题(单调队列优化)6.剖分问题(多边形剖分/石子合并/圆的剖分/乘积最大)<1>凸多边形的三角剖分问题<2>乘积最大问题<3>多边形游戏(多边形边上是操作符,顶点有权值)<4>石子合并(N^3/N^2/NLogN各种优化)7.贪心的动态规划<1>最优装载问题<2>部分背包问题<3>乘船问题<4>贪心策略<5>双机调度问题Johnson算法8.状态dp<1>牛仔射击问题(博弈类)<2>哈密顿路径的状态dp<3>两支点天平平衡问题<4>一个有向图的最接近二部图9.树型dp<1>完美服务器问题(每个节点有3种状态)<2>小胖守皇宫问题<3>网络收费问题<4>树中漫游问题<5>树上的博弈<6>树的最大独立集问题<7>树的最大平衡值问题<8>构造树的最小环(二):麻烦题:1697, 1712, 1713, 1720, 1729, 1765, 1772, 1858, 1872, 1960, 1963, 2050, 2122, 2162, 22 19, 2237,简单题目:1000, 1003, 1004, 1005, 1007, 1046, 1207, 1226, 1401, 1504, 1552, 1607, 1657, 1658, 16 74, 1799, 1862, 1906, 1922, 1929, 1931, 1969, 1976, 2000, 2005, 2017, 2027, 2070, 2101, 2105, 2109, 2116, 2136, 2160, 2190, 2232, 2234, 2275, 2301, 2350, 2363, 2389, 2393, 2 413, 2419,推荐:1063, 1064, 1131, 1140, 1715, 2163,杂题:1014, 1218, 1316, 1455, 1517, 1547, 1580, 1604, 1663, 1678, 1749, 1804, 2013, 2014, 20 56, 2059, 2100, 2188, 2189, 2218, 2229, 2249, 2290, 2302, 2304, 2309, 2313, 2316, 2323, 2326, 2368, 2369, 2371, 2402, 2405, 2407,推荐:1146, 1147, 1148, 1171, 1389, 1433, 1468, 1519, 1631, 1646, 1672, 1681, 1700, 1701, 17 05, 1728, 1735, 1736, 1752, 1754, 1755, 1769, 1781, 1787, 1796, 1797, 1833, 1844, 1882, 1933, 1941, 1978, 2128, 2166, 2328, 2383, 2420,高精度:1001, 1220, 1405, 1503,排序:1002, 1318, 1877, 1928, 1971, 1974, 1990, 2001, 2002, 2092, 2379, 2388, 2418,推荐:1423, 1694, 1723, 1727, 1763, 1788, 1828, 1838, 1840, 2201, 2376, 2377, 2380,搜索1676,1376,@3009,容易:1128, 1166, @1176, 1231, 1256, @1270, 1321, @1543, 1606, @1664, 1731, 1742, @174 5, 1847, 1915, 1950, 2038, 2157, 2182, 2183, 2381, 2386, 2426,不易:1024, 1054, 1117, 1167, 1708, 1746, 1775, 1878, 1903, 1966, 2046, 2197, 2349,推荐:1011, 1190, 1191, 1416, 1579, 1632, 1639, 1659, 1680, 1683, 1691, 1709, 1714, 1753, 17 71, 1826, 1855, 1856, 1890, 1924, 1935, 1948, 1979, 1980, 2170, 2288, 2331, 2339, 2340,数据结构容易:1182, 1656, 2021, 2023, 2051, 2153, 2227, 2236, 2247, 2352, 2395,不易:1145, 1177, 1195, 1227, 1661, 1834,推荐:1330, @1338, 1451, 1470, 1634, 1689, 1693, @1703, 1724, 1988, 2004, 2010(堆), 2119, 2274,动态规划容易:1018, 1050, 1083, 1088, 1125, 1143(博弈树), 1157, @1163, 1178, 1179, @1189, 1208, 1276, 1322, 1414, 1456, 1458, 1609, 1644, 1664, 1690, 1699, 1740, 1742, 1887, 1926, 19 36, 1952, 1953, 1958, 1959, 1962, 1975, 1989, 2018, 2029, 2033, 2063, 2081, 2082, 2181, 2184, 2192, 2231, 2279, 2329, 2336, 2346, 2353, 2355, 2356, 2385, 2392, 2424,不易:1019, 1037, 1080, 1112, 1141, 1170, 1192, 1239, 1655, 1695, 1707, 1733, 1737, 1837, 18 50, 1920, 1934, 1937, 1964, 2039, 2138, 2151, 2161, 2178,推荐:1015, 1635, 1636, 1671, 1682, 1692, 1704, 1717, 1722, 1726, 1732, 1770, 1821, 1853, 19 49, 2019, 2127, 2176, 2228, 2287, 2342, 2374, 2378, 2384, 2411,字符串:1488, ⊙1598, 1686, *1706, 1747, 1748, 1750, 1760, 1782, 1790, 1866, 1888, 1896, 1951, 2003, 2121, 2141, 2145, 2159, 2337, 2359, 2372, 2406, 2408,贪心:1042, 1065, 1230, 1323, 1477, 1716, 1784,图论容易:1161, 1164, 1258, 1175, 1308, 1364, 1776, 1789, 1861, 1939, 1940, 1943, 2075, 2139, 23 87, 2394, 2421,不易:1041, 1062, 1158, 1172, 1201, 1275, 1718, 1734, 1751, 1904, 1932, 2173, 2175, 2296,网络流:1087, 1273, 1698, 1815, 2195,匹配:1274, 1422, 1469, 1719, 2060, 2239,Euler:1237, 1637, 1394, 2230,推荐:2049, 2186,计算几何容易:@1319, @1654, @1673, @1675, 1836, 2074, 2137, 2318,不易:1685, 1687, 1696, 1873, 1901, 2172, 2333,凸包:1113, 1228, 1794, 2007, 2187,模拟容易:1006, 1008, 1013, 1016, 1017, 1169, 1298, 1326, 1350, 1363, 1676, 1786, 1791, 1835, 19 70, 2317, 2325, 2390,不易:1012, 1082, 1099, 1114, 1642, 1677, 1684, 1886,数学容易:@1061, @1091, @1142, 1289, @1305, @1306, 1320, @1565, @1665, 1666, @1730, @18 94, @1914, 2006, @2042, @2142, 2158, 2174, @2262, @2305, @2321, @2348,不易:@1067, @1183, 1430, 1759, 1868, 1942, 2167, 2171, 2327,推荐:@1423, 1450, 1640, @1702, 1710, 1721, 1761, 1830, @1930, @2140,(三):1、排序1423, 1694, 1723, 1727, 1763, 1788, 1828, 1838, 1840, 2201, 2376, 2377, 2380, 1318, 18 77, 1928, 1971, 1974, 1990, 2001, 2002, 2092, 2379, 1002(需要字符处理,排序用快排即可)1007(稳定的排序)2159(题意较难懂)2231 2371(简单排序)2388(顺序统计算法)2418(二叉排序树)2、搜索、回溯、遍历1022 1111 1118 1129 1190 1562 1564 1573 1655 2184 2225 2243 2312 2362 2378 2386 1010,1011,1018,1020,1054,1062,1256,1321,1363,1501,1650,1659,1664,1753,2078,2083,2303,2 310,2329简单:1128, 1166, 1176, 1231, 1256, 1270, 1321, 1543, 1606, 1664, 1731, 1742, 1745, 18 47, 1915, 1950, 2038, 2157, 2182, 2183, 2381, 2386, 2426,不易:1024, 1054, 1117, 1167, 1708, 1746, 1775, 1878, 1903, 1966, 2046, 2197, 2349,推荐:1011, 1190, 1191, 1416, 1579, 1632, 1639, 1659, 1680, 1683, 1691, 1709, 1714, 17 53, 1771, 1826, 1855, 1856, 1890, 1924, 1935, 1948, 1979, 1980, 2170, 2288, 2331, 2339, 2340,1979(和迷宫类似)1980(对剪枝要求较高)3、历法1008 2080 (这种题要小心)4、枚举1012,1046,1387,1411,2245,2326,2363,2381,1054(剪枝要求较高),165 0 (小数的精度问题)5、数据结构的典型算法容易:1182, 1656, 2021, 2023, 2051, 2153, 2227, 2236, 2247, 2352, 2395,不易:1145, 1177, 1195, 1227, 1661, 1834,推荐:1330, 1338, 1451, 1470, 1634, 1689, 1693, 1703, 1724, 1988, 2004, 2010, 2119, 22 74,1125(弗洛伊德算法) ,2421(图的最小生成树)6、动态规划1037、1050、1088、1125、1141、1159、1160、1163、1458、1579 、1887 、1953 、2386 7、贪心1042, 1065, 1230, 1323, 1477, 1716, 1784,1328 1755(或用单纯形方法),2054,1017,1328,1862,1922 ,2209,2313,2325,2370。

初期:一.基本算法:(1)枚举. (poj1753,poj2965)(2)贪心(poj1328,poj2109,poj2586)(3)递归和分治法.(4)递推.(5)构造法.(poj3295)(6)模拟法.(poj1068,poj2632,poj1573,poj2993,poj2996)二.图算法:(1)图的深度优先遍历和广度优先遍历.(2)最短路径算法(dijkstra,bellman-ford,floyd,heap+dijkstra)(poj1860,poj3259,poj1062,poj2253,poj1125,poj2240)(3)最小生成树算法(prim,kruskal) (poj1789,poj2485,poj1258,poj3026)(4)拓扑排序 (poj1094)(5)二分图的最大匹配 (匈牙利算法) (poj3041,poj3020)(6)最大流的增广路算法(KM算法). (poj1459,poj3436)三.数据结构.(1)串 (poj1035,poj3080,poj1936)(2)排序(快排、归并排(与逆序数有关)、堆排) (poj2388,poj2299)(3)简单并查集的应用.(4)哈希表和二分查找等高效查找法(数的Hash,串的Hash)(poj3349,poj3274,POJ2151,poj1840,poj2002,poj2503)(5)哈夫曼树(poj3253)(6)堆(7)trie树(静态建树、动态建树) (poj2513)四.简单搜索(1)深度优先搜索 (poj2488,poj3083,poj3009,poj1321,poj2251)(2)广度优先搜索(poj3278,poj1426,poj3126,poj3087.poj3414)(3)简单搜索技巧和剪枝(poj2531,poj1416,poj2676,1129)五.动态规划(1)背包问题. (poj1837,poj1276)(2)型如下表的简单DP(可参考lrj的书 page149):1.E[j]=opt{D+w(i,j)} (poj3267,poj1836,poj1260,poj2533)2.E[i,j]=opt{D[i-1,j]+xi,D[i,j-1]+yj,D[i-1][j-1]+zij} (最长公共子序列) (poj3176,poj1080,poj1159)3.C[i,j]=w[i,j]+opt{C[i,k-1]+C[k,j]}.(最优二分检索树问题)六.数学(1)组合数学:1.加法原理和乘法原理.2.排列组合.3.递推关系.(POJ3252,poj1850,poj1019,poj1942)(2)数论.1.素数与整除问题2.进制位.3.同余模运算.(poj2635, poj3292,poj1845,poj2115)(3)计算方法.1.二分法求解单调函数相关知识.(poj3273,poj3258,poj1905,poj3122)七.计算几何学.(1)几何公式.(2)叉积和点积的运用(如线段相交的判定,点到线段的距离等). (poj2031,poj1039)(3)多边型的简单算法(求面积)和相关判定(点在多边型内,多边型是否相交)(poj1408,poj1584)(4)凸包. (poj2187,poj1113)中级:一.基本算法:(1)C++的标准模版库的应用. (poj3096,poj3007)(2)较为复杂的模拟题的训练(poj3393,poj1472,poj3371,poj1027,poj2706)二.图算法:(1)差分约束系统的建立和求解. (poj1201,poj2983)(2)最小费用最大流(poj2516,poj2516,poj2195)(3)双连通分量(poj2942)(4)强连通分支及其缩点.(poj2186)(5)图的割边和割点(poj3352)(6)最小割模型、网络流规约(poj3308, )三.数据结构.(1)线段树. (poj2528,poj2828,poj2777,poj2886,poj2750)(2)静态二叉检索树. (poj2482,poj2352)(3)树状树组(poj1195,poj3321)(4)RMQ. (poj3264,poj3368)(5)并查集的高级应用. (poj1703,2492)(6)KMP算法. (poj1961,poj2406)四.搜索(1)最优化剪枝和可行性剪枝(2)搜索的技巧和优化 (poj3411,poj1724)(3)记忆化搜索(poj3373,poj1691)五.动态规划(1)较为复杂的动态规划(如动态规划解特别的施行商问题等) (poj1191,poj1054,poj3280,poj2029,poj2948,poj1925,poj3034)(2)记录状态的动态规划. (POJ3254,poj2411,poj1185)(3)树型动态规划(poj2057,poj1947,poj2486,poj3140)六.数学(1)组合数学:1.容斥原理.2.抽屉原理.3.置换群与Polya定理(poj1286,poj2409,poj3270,poj1026).4.递推关系和母函数.(2)数学.1.高斯消元法(poj2947,poj1487, poj2065,poj1166,poj1222)2.概率问题. (poj3071,poj3440)3.GCD、扩展的欧几里德(中国剩余定理) (poj3101)(3)计算方法.1.0/1分数规划. (poj2976)2.三分法求解单峰(单谷)的极值.3.矩阵法(poj3150,poj3422,poj3070)4.迭代逼近(poj3301)(4)随机化算法(poj3318,poj2454)(5)杂题. (poj1870,poj3296,poj3286,poj1095)七.计算几何学.(1)坐标离散化.(2)扫描线算法(例如求矩形的面积和周长并,常和线段树或堆一起使用).(poj1765,poj1177,poj1151,poj3277,poj2280,poj3004)(3)多边形的内核(半平面交)(poj3130,poj3335)(4)几何工具的综合应用.(poj1819,poj1066,poj2043,poj3227,poj2165,poj3429)高级:一.基本算法要求:(1)代码快速写成,精简但不失风格(poj2525,poj1684,poj1421,poj1048,poj2050,poj3306)(2)保证正确性和高效性. poj3434二.图算法:(1)度限制最小生成树和第K最短路. (poj1639)(2)最短路,最小生成树,二分图,最大流问题的相关理论(主要是模型建立和求解) (poj3155, poj2112,poj1966,poj3281,poj1087,poj2289,poj3216,poj2446) (3)最优比率生成树. (poj2728)(4)最小树形图(poj3164)(5)次小生成树.(6)无向图、有向图的最小环三.数据结构.(1)trie图的建立和应用. (poj2778)(2)LCA和RMQ问题(LCA(最近公共祖先问题) 有离线算法(并查集+dfs) 和在线算法(RMQ+dfs)).(poj1330)(3)双端队列和它的应用(维护一个单调的队列,常常在动态规划中起到优化状态转移的目的).(poj2823)(4)左偏树(可合并堆).(5)后缀树(非常有用的数据结构,也是赛区考题的热点). (poj3415,poj3294)四.搜索(1)较麻烦的搜索题目训练(poj1069,poj3322,poj1475,poj1924,poj2049,poj3426)(2)广搜的状态优化:利用M进制数存储状态、转化为串用hash表判重、按位压缩存储状态、双向广搜、A*算法. (poj1768,poj1184,poj1872,poj1324,poj2046,poj1482)(3)深搜的优化:尽量用位运算、一定要加剪枝、函数参数尽可能少、层数不易过大、可以考虑双向搜索或者是轮换搜索、IDA*算法.(poj3131,poj2870,poj2286)五.动态规划(1)需要用数据结构优化的动态规划. (poj2754,poj3378,poj3017)(2)四边形不等式理论.(3)较难的状态DP(poj3133)六.数学(1)组合数学.1.MoBius反演(poj2888,poj2154)2.偏序关系理论.(2)博奕论.1.极大极小过程(poj3317,poj1085)2.Nim问题.七.计算几何学.(1)半平面求交(poj3384,poj2540)(2)可视图的建立(poj2966)(3)点集最小圆覆盖.(4)对踵点(poj2079)八.综合题.(poj3109,poj1478,poj1462,poj2729,poj2048,poj3336,poj3315,poj2148,poj1263) 以及补充Dp状态设计与方程总结1.不完全状态记录<1>青蛙过河问题<2>利用区间dp2.背包类问题<1> 0-1背包,经典问题<2>无限背包,经典问题<3>判定性背包问题<4>带附属关系的背包问题<5> + -1背包问题<6>双背包求最优值<7>构造三角形问题<8>带上下界限制的背包问题(012背包)3.线性的动态规划问题<1>积木游戏问题<2>决斗(判定性问题)<3>圆的最大多边形问题<4>统计单词个数问题<5>棋盘分割<6>日程安排问题<7>最小逼近问题(求出两数之比最接近某数/两数之和等于某数等等)<8>方块消除游戏(某区间可以连续消去求最大效益)<9>资源分配问题<10>数字三角形问题<11>漂亮的打印<12>邮局问题与构造答案<13>最高积木问题<14>两段连续和最大<15>2次幂和问题<16>N个数的最大M段子段和<17>交叉最大数问题4.判定性问题的dp(如判定整除、判定可达性等)<1>模K问题的dp<2>特殊的模K问题,求最大(最小)模K的数<3>变换数问题5.单调性优化的动态规划<1>1-SUM问题<2>2-SUM问题<3>序列划分问题(单调队列优化)6.剖分问题(多边形剖分/石子合并/圆的剖分/乘积最大)<1>凸多边形的三角剖分问题<2>乘积最大问题<3>多边形游戏(多边形边上是操作符,顶点有权值)<4>石子合并(N^3/N^2/NLogN各种优化)7.贪心的动态规划<1>最优装载问题<2>部分背包问题<3>乘船问题<4>贪心策略<5>双机调度问题Johnson算法8.状态dp<1>牛仔射击问题(博弈类)<2>哈密顿路径的状态dp<3>两支点天平平衡问题<4>一个有向图的最接近二部图9.树型dp<1>完美服务器问题(每个节点有3种状态)<2>小胖守皇宫问题<3>网络收费问题<4>树中漫游问题<5>树上的博弈<6>树的最大独立集问题<7>树的最大平衡值问题<8>构造树的最小环转一个搞ACM需要的掌握的算法.要注意,ACM的竞赛性强,因此自己应该和自己的实际应用联系起来.适合自己的才是好的,有的人不适合搞算法,喜欢系统架构,因此不要看到别人什么就眼红, 发挥自己的长处,这才是重要的.第一阶段:练经典常用算法,下面的每个算法给我打上十到二十遍,同时自己精简代码,因为太常用,所以要练到写时不用想,10-15分钟内打完,甚至关掉显示器都可以把程序打出来.1.最短路(Floyd、Dijstra,BellmanFord)2.最小生成树(先写个prim,kruscal要用并查集,不好写)3.大数(高精度)加减乘除4.二分查找. (代码可在五行以内)5.叉乘、判线段相交、然后写个凸包.6.BFS、DFS,同时熟练hash表(要熟,要灵活,代码要简)7.数学上的有:辗转相除(两行内),线段交点、多角形面积公式.8. 调用系统的qsort, 技巧很多,慢慢掌握.9. 任意进制间的转换第二阶段:练习复杂一点,但也较常用的算法。


网络最大流的算法网络最大流的算法分类:一、Ford-Fulkerson增广路方法1、Ford-Fulkerson标号算法(最简单的实现)分别记录这一轮扩展过程中的每个点的前驱与到该节点的增广最大流量,从源点开始扩展,每次选择一个点(必须保证已经扩展到这个点),检查与它连接的所有边,并进行扩展,直到扩展到t。
2、最大容量增广路算法每次找一条容量最大的增广路来增广,找的过程类似Dijkstra,实现起来相当简单。
3、Edmonds-Karp,最短路增广算法的BFS实现每次找一条最短的增广路,BFS是一个可以很方便的实现思想。
4、距离标号算法最短路增广的O(n)寻找实现,使用距离函数d:d[t]=0;d<=d[j]+1若存在(i,j)∈E;只有路径上满足d=d[i+1]+1的增广路才为满足要求的,一开始我们初始化使标号恰好满足要求,之后不断更改标号使其可以使增广继续。
5、Dinic,分层思想对网络分层(按照距t的距离),保留相邻层之间的边,然后运用一次类似于距离标号的方法(其实质是DFS)进行增广。
二、预留与推进算法1、一般性算法随便找个点,要么将他的盈余推出去,要么对他进行重标记,直至无活跃点为止。
2、重标记与前移算法维护一个队列,对一个点不断进行推进与重标记操作,直至其盈余为0,若过程中他没有被重标记过,则可出列,否则加入队头,继续等待检查。
3、最高标号预留与推进算法记录d值,然后优先处理d值较高的,直至没有盈余。
网络最大流的算法实现一、Edmonds-Karp(EK)算法就是用广度优先搜索来实现Ford-Fulkerson方法中对增广路径的计算,时间复杂度为O(VE2),Shortest Augmenting Path (SAP) 是每次寻找最短增广路的一类算法,Edmonds - Karp 算法以及后来著名的Dinic 算法都属于此。
SAP 类算法可统一描述如下:Shortest Augmenting Path{ x <-- 0while 在残量网络Gx 中存在增广路s ~> t do{ 找一条最短的增广路径Pdelta <-- min{rij:(i,j) 属于P}沿P 增广delta 大小的流量更新残量网络Gx}return x}在无权边的有向图中寻找最短路,最简单的方法就是广度优先搜索(BFS),E-K 算法就直接来源于此。

km算法⽹络流 km算法什么是⽹络流?⽹络流指,存在⼀个源点s和⼀个汇点t的特殊有向⽆环图(TAG),虽然说有图会好很多但是毕竟我只是写着为了之后忘了有回顾的东西,⽽且好⿇烦..那什么是⽹络流的最⼤流?⽹络流的最⼤流是指这个⽹络流允许通过的最⼤流(有点重复定义的感觉,不过定义好像也是望⽂⽣义)⽹络流的km算法⽤于解决⽹络流的最⼤流问题km算法那怎么解决这个问题呢,参考⼆分图中增⼴路的想法。
假如从源点bfs发现可以到达汇点,说明这是⼀条可以被开发的路,那么ans就要加上这个路径中所有边的容量最⼩值(短板效应)但是很明显,怎么可能⼀bfs就bfs成最优规划?bfs肯定会导致某些本不该流的边有流量,⼜或者本应该流的边在别的边的影响下流量枯竭(联通⼤王卡,限速⼜限流,真⾹)所以就需要引⼊⼀个反悔机制,让路径有删除流量的可能,为此:在原来的⼀条边之外(u->v),引⼊⼀条反边(v->u),翻边的权值为u,v之间的容量减去正边的流量,即已经在这条边上流过的流量,也可以理解为可以反悔的容量到此为之,算法就有了雏形:1.不断bfs判断是否存在增⼴路,若不存在,说明当前已达到了最⼤流2.若存在,就需要从容量中,把这些流量减去3.对于经过的所有边,正边的容量减去该容量,意为剩余流量减少,对于所有反边,加上该容量,意为可以返回的边增加4.ans+=流量代码也是相当易懂个蛋int BFS(int src,int des){int i,j;while(!myqueue.empty()) //队列清空myqueue.pop();for(i=1;i<m+1;++i){pre[i]=-1;}pre[src]=0;flow[src]= maxData;myqueue.push(src);while(!myqueue.empty()){int index = myqueue.front();myqueue.pop();if(index == des) //找到了增⼴路径break;for(i=1;i<m+1;++i){if(i!=src && capacity[index][i]>0 && pre[i]==-1){pre[i] = index; //记录前驱flow[i] = min(capacity[index][i],flow[index]); //关键:迭代的找到增量myqueue.push(i);}}}if(pre[des]==-1) //残留图中不再存在增⼴路径return -1;elsereturn flow[des];}int maxFlow(int src,int des){int increasement= 0;int sumflow = 0;while((increasement=BFS(src,des))!=-1){int k = des; //利⽤前驱寻找路径while(k!=src){int last = pre[k];capacity[last][k] -= increasement; //改变正向边的容量capacity[k][last] += increasement; //改变反向边的容量 k = last;}sumflow += increasement;}return sumflow;}⾄此 o( ̄▽ ̄)o。


⽹络流(⼆)最⼤流的增⼴路算法传送门:⽹络流的相关定义:源点:有n个点,有m条有向边,有⼀个点很特殊,只出不进,叫做源点。
汇点:另⼀个点也很特殊,只进不出,叫做汇点。
容量和流量:每条有向边上有两个量,容量和流量,从i到j的容量通常⽤c[i,j]表⽰,流量则通常是f[i,j].通常可以把这些边想象成道路,流量就是这条道路的车流量,容量就是道路可承受的最⼤的车流量。
很显然的,流量<=容量。
⽽对于每个不是源点和汇点的点来说,可以类⽐的想象成没有存储功能的货物的中转站,所有“进⼊”他们的流量和等于所有从他本⾝“出去”的流量。
最⼤流:把源点⽐作⼯⼚的话,问题就是求从⼯⼚最⼤可以发出多少货物,是不⾄于超过道路的容量限制,也就是,最⼤流。
求解思路:⾸先,假如所有边上的流量都没有超过容量(不⼤于容量),那么就把这⼀组流量,或者说,这个流,称为⼀个可⾏流。
⼀个最简单的例⼦就是,零流,即所有的流量都是0的流。
(1).我们就从这个零流开始考虑,假如有这么⼀条路,这条路从源点开始⼀直⼀段⼀段的连到了汇点,并且,这条路上的每⼀段都满⾜流量<容量,注意,是严格的<,⽽不是<=。
(2).那么,我们⼀定能找到这条路上的每⼀段的(容量-流量)的值当中的最⼩值delta。
我们把这条路上每⼀段的流量都加上这个delta,⼀定可以保证这个流依然是可⾏流,这是显然的。
(3).这样我们就得到了⼀个更⼤的流,他的流量是之前的流量+delta,⽽这条路就叫做增⼴路。
我们不断地从起点开始寻找增⼴路,每次都对其进⾏增⼴,直到源点和汇点不连通,也就是找不到增⼴路为⽌。
(4).当找不到增⼴路的时候,当前的流量就是最⼤流,这个结论⾮常重要。
补充:(1).寻找增⼴路的时候我们可以简单的从源点开始做BFS,并不断修改这条路上的delta 量,直到找到源点或者找不到增⼴路。
(2).在程序实现的时候,我们通常只是⽤⼀个c 数组来记录容量,⽽不记录流量,当流量+delta 的时候,我们可以通过容量-delta 来实现,以⽅便程序的实现。
km算法原理KM算法原理:带权二分图最大权完美匹配KM算法全称为Kuhn-Munkres算法,是一种求解带权二分图最大权完美匹配的算法。
该算法的时间复杂度为O(n^3),相较于暴力枚举的O(n!)和网络流的O(n^4),其效率更高。
我们来了解一下什么是带权二分图。
带权二分图是指一个无向图G=(V, E),其中V可以划分为两个集合X和Y,使得X和Y内部的点没有边相连,而X和Y之间的点有边相连,并且每条边都有一个权值。
我们的目标是找到X到Y的最大权匹配。
KM算法的思路是不断尝试寻找增广路,并将其加入当前匹配中。
增广路是指从未匹配的点开始,经过一系列已匹配的点,最终到达另一个未匹配的点的路径。
如果当前匹配中不存在增广路,那么我们就找到了最大权匹配。
具体实现时,我们需要使用两个数组:lx和ly。
lx[i]表示左边第i个点的最大权值,ly[j]表示右边第j个点的最大权值。
初始时,我们将lx[i]=max{w[i][j]},其中w[i][j]表示左边第i个点到右边第j个点的边权值,ly[j]=0。
然后我们不断进行匹配,直到没有增广路为止。
匹配的过程中,我们需要使用一个vis数组记录右边第j个点是否被访问过。
如果右边第j个点未被访问,我们就尝试匹配左边第i个点和右边第j个点,如果匹配成功,就更新lx[i]和ly[j]的值。
如果匹配失败,我们就需要尝试将当前匹配中的某个点切换到另一个点上,以获得更大的权值。
这个过程可以通过递归实现。
我们得到的匹配就是带权二分图的最大权完美匹配。
KM算法的时间复杂度为O(n^3),空间复杂度为O(n^2)。
KM算法是一种高效的求解带权二分图最大权完美匹配的算法。
它的思路简单,实现也不难,但需要注意细节和边界条件。
在实际应用中,KM算法可以用于匹配问题、优化问题等方面。
求解最大流问题的算法和模型最大流问题是图论中的一个基本问题,涉及到网络流的计算和优化。
在实际应用中,最大流问题的求解涉及到诸多算法和模型,如增广路径算法、Ford-Fulkerson算法、Dinic算法、最小割定理等。
本文将从这些方面进行论述。
1. 增广路径算法增广路径算法是求解最大流问题的经典算法,其基本思想是不断地寻找增广路径,通过增加路径上的流量来增加整个网络的流量。
具体来说,首先通过深度优先搜索或广度优先搜索找到一条从源点到汇点的增广路径,然后确定路径上的最小流量d,将当前流量增加d,将反向边的流量减少d,同时计算当前网络的流量。
2. Ford-Fulkerson算法Ford-Fulkerson算法是一种经典的增广路径算法,其基本理念与增广路径算法相同,但采用不同的策略来确定增广路径。
具体来说,Ford-Fulkerson算法采用贪心策略,在每次迭代中选择路径上的最小容量,从而确定增加的流量。
此外,Ford-Fulkerson算法还引入了残量图的概念,用于计算增广路径的容量。
3. Dinic算法Dinic算法是一种高效的增广路径算法,其主要优点是采用了分层图的策略来确定增广路径,使得每次迭代的搜索范围大为缩小。
具体来说,Dinic算法首先利用BFS算法确定每个节点的分层,然后在分层图上通过DFS算法查找增广路径,在路径上增加流量,更新分层图,重复此过程直至求解最大流。
4. 最小割定理最小割定理是求解最大流问题的重要定理,其核心思想是将网络分成两个不相交部分,并将其最小的割称为最小割。
最小割定理指出,在任意网络中,最大流等于最小割。
因此,求解最大流可以转化为求最小割问题,即在网络中寻找一组最小割,使得所有的割中容量最小的一组割。
总之,求解最大流问题是图论中的一个重要问题,其求解涉及到诸多算法和模型,如增广路径算法、Ford-Fulkerson算法、Dinic 算法、最小割定理等。
在实际应用中,不同情况下可能需要采用不同的算法和模型来求解,需要灵活应用。
km(kuhn-munkres)算法的具体表达KM算法,即Kuhn-Munkres算法(又称为匈牙利算法),是一种用于求解二分图最大权匹配问题的经典算法。
它由Eugene L. Lawler于1960年首次提出,后来由James Munkres在1957年独立发表,因此常称为Kuhn-Munkres算法。
二分图最大权匹配问题是指给定一个带权二分图,要求在图中选取权重之和最大的边集合,使得任意两条边不属于同一个顶点。
其中,带权二分图是指图的每条边都带有一个非负权重。
KM算法使用了两个关键的概念:交错树和相等子图。
交错树是指一个T=(S,P)的有向树,其中S是原二分图的所有顶点的集合,P是树中的边集合。
相等子图是指原二分图的一个子图,其中T中所有入树边的权重之和等于所有出树边的权重之和。
KM算法具体的步骤如下:1.初始化:将图中所有边的权重初始化为0,构建了一个初始的交错树T=(X,Y)(其中X,Y分别表示两个顶点集合)。
2.判断相等子图:对于T中的每个顶点x,如果存在一条满足lx+ly=W(其中lx是x在T中所有入树边的权重之和,ly是x在T中所有出树边的权重之和,W是x在原图G中的权重),则把x加入到相等子图中。
3.寻找未匹配节点:在相等子图中寻找未匹配节点,并标记为未父节点。
4.寻找增广路:如果存在未匹配节点,则从中选择一个起始节点,寻找一条与之交替出现的边构成的路径,使路径的最后一个边是一条与未匹配节点关联的边。
这样的路径称为增广路。
5.修改标号:对于相等子图中的每个顶点x,从已匹配节点中选择一个与之关联的顶点y,并计算d=min(lx+ly-w)(其中w是x和y之间的边的权重),为了使增广路更优,将T中所有x节点的入树边的权重减去d,将T中所有y节点的出树边的权重加上d。
6.更新交错树:将增广路中的所有边和T中的所有非树边进行调整,得到新的交错树。
7.重复步骤3-6,直到没有未匹配节点为止。
运筹学最大流问题实验报告一、实验目的1. 学习最大流问题的基本概念。
2. 掌握最大流问题的求解算法。
3. 通过程序模拟求解,加深对最大流问题的理解。
二、实验原理最大流问题是在一个有向图中,给定一条源点到汇点的路径以及每一条边的最大容量,求最大流量的问题。
在网络流中,每个有向边都表示一定的流量,其中每个边的构成是(开始节点,结束节点,最大容量)。
最大流问题通常使用增广路算法或Ford-Fulkerson算法来求解。
1.增广路算法增广路算法是一种贪心算法。
该算法不断寻找一条增广路,并将增广路中的最小流量分配给这条增广路的每一条边。
当不存在增广路时,算法结束,返回最大流量。
2.Ford-Fulkerson算法Ford-Fulkerson算法是一种经典的解法,它是基于增广路径的算法。
但是这种算法是暴力寻求增广路径,时间复杂度较高。
需要借助一个可行函数,用来判断剩余网络中是否还有增广路。
一个网络的可行函数应该满足:当且仅当所有的边都满足限制的时候,可行函数有唯一最大值。
可行函数常常构建为距离标号(下面会讲到)。
三、实验步骤使用Python语言,实现最大流问题的求解算法。
算法采用增广路算法。
1. 构建有向图,每个节点可以表示为一个数字。
源点的编号为0,汇点的编号为N-1。
有向边的构成是(开始节点,结束节点,最大容量)。
2. 实现BFS广度优先搜索算法寻找增广路径。
3. 实现对路径上节点的最小流量计算并更新网络。
4. 不断循环执行2、3步骤,直到不存在增广路径为止。
5. 输出最大流量。
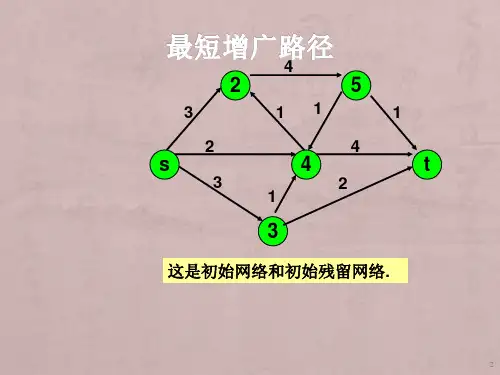
四、实验结果下面是一个简单的实例,以验证程序的正确性。
在这个网络中,从源点0到汇点5,可以有两条不同路径:0→1→2→4→5和0→1→3→4→5。
这两条路径中,最小容量的路径是第一条,容量为3。
在执行完毕后,程序输出了最大流量为3。
五、实验结论通过本实验,我们学习了最大流问题的基本概念,掌握了最大流问题的求解算法,并且通过程序模拟成功地求解了一个基本问题,加深了对最大流问题的理解。
⽹络流之最⼤流的增⼴路径算法扩展:多路增⼴⼀般的,在执⾏增⼴路算法时,都是先⽤BFS或DFS从源到汇找到⼀条增⼴路,记录下应修改的流量,然后再顺着路倒回去增⼴.反复这个过程直到增⼴路找不到了为⽌.显然的,我们做了很多⽆⽤功,假设有两条很长的增⼴路,前⾯⼤部分都是重叠的,只是在最后关头分了个岔,⽽程序却把前⾯很长的路⾛了两次.为什么要这样?不妨把两条增⼴路合并起来,不⽌是两条,所有的增⼴路都可以按其前缀合并起来,⽽形成⼀棵增⼴树.找增⼴树可以⽤DFS,正如⽣成搜索树⼀样.简⽽⾔之,对于当前的每⼀个结点记录⼀个可提供的最⼤流量,源点的可供流量显然是⽆穷⼤,当推到下⼀个点时,最⼤流量取边的容量和上个点提供的最⼤流量的较⼩值.当到达汇点时,⾃然DFS开始回朔,这时按当前点的已⽤流量增⼴当前点与他⽗亲相连的边,同时将增⼴值累加到他⽗亲的已⽤流量上,并在他⽗亲的可提供流量上减掉这个值,以便在搜索他⽗亲剩下的⼉⼦时,让所有⼉⼦的已⽤流量总和不⼤于⽗亲的可提供流量,不然就出错了.我们按照以下步骤做:search node(available){1.得到node的可提供流量available2.search node's all son(可提供流量){inc(已⽤流量,当前⼉⼦实际增⼴的流量)dec(可提供流量,<同上>)}3.⽤得到的已⽤流量的值增⼴边(node-node's father)4.return 边的增⼴量到 node'fahter}每进⾏⼀次以上步骤,我们就完成了⼀次多路增⼴,并且返回了⼀个值到源点,即DFS的根.这个值表⽰本次操作中将流量扩⼤了多少.重复操作直到返回值为0.得到最⼤流的数值即累加每次的返回值.#include <iostream>#include <queue>#define msize 1024 //最⼤顶点数⽬using namespace std;int d[msize];//标号int r[msize][msize];//残留⽹络,初始为原图int num[msize];//num[i]表⽰标号为i的顶点数有多少int pre[msize];int n,m,s,t;//m个顶点,n条边,从源点s到汇点tvoid ini_d()//BFS计算标号,汇点t标号为0{int k;queue<int>Q;memset(d,1,sizeof(d));memset(num,0,sizeof(num));Q.push(t);d[t]=0;num[0]=1;while(!Q.empty()){k=Q.front(),Q.pop();for(int i=0;i<m;i++){if(d[i]>=m&&r[i][k]>0){d[i]=d[k]+1;Q.push(i);num[d[i]]++;}}}}int findAlowArc(int i)//从i出发寻找允许弧{int j;for(j=0;j<m;j++)if(r[i][j]>0&&d[i]==d[j]+1)return j;return-1;}int reLable(int i)//重新标号{int mm=INT_MAX;for(int j=0;j<m;j++)if(r[i][j]>0) mm=min(mm,d[j]+1);return mm==INT_MAX?m:mm;}int maxFlow(int s,int t)//从源点s出发的最⼤流{int flow=0,i=s,j;int delta;//增量memset(pre,-1,sizeof(pre));while(d[s]<m){j=findAlowArc(i);if(j>=0){pre[j]=i;i=j;if(i==t)//更新残留⽹络{delta=INT_MAX;for(i=t;i!=s;i=pre[i])delta=min(delta,r[pre[i]][i]);for(i=t;i!=s;i=pre[i])r[pre[i]][i]-= delta, r[i][pre[i]]+= delta;flow += delta;}}else{int x=reLable(i);//重新标号num[x]++;num[d[i]]–;if(num[d[i]]==0)return flow;//间隙优化d[i]=x;if(i!=s) i=pre[i];}}return flow;}FF算法分为三个步骤,⾸先寻找⼀条增⼴路(如果没有增⼴路,则返回最⼤流),同时保存路径;其次,对路径上的流量求最⼩值,记为min;最后根据路径修改⽹络,对于前向边,减去最⼩值,对于后向边,加上最⼩值,或者直接修改容量。
1459:Power NetworkTime Limit: 2000MS Memory Limit: 32768KTotal Submissions: 17697 Accepted: 9349 DescriptionA power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amounts(u) >= 0 of power, may produce an amount 0 <= p(u) <= p max(u) of power, may consume an amount 0 <= c(u) <= min(s(u),c max(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= l max(u,v) of power delivered by u to v. LetCon=Σu c(u) be the power consumed in the net. The problem is to compute the maximum value of Con.An example is in figure 1. The label x/y of power station u shows that p(u)=x andp max(u)=y. The label x/y of consumer u shows that c(u)=x and c max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6.InputThere are several data sets in the input. Each data set encodes a power network. It starts with four integers: 0 <= n <= 100 (nodes), 0 <= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <= n^2 (power transport lines). Follow m data triplets (u,v)z, where u and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the value of l max(u,v). Follow np doublets (u)z, where u is the identifier of a power station and 0 <= z <= 10000 is the value of p max(u). The data set ends with nc doublets (u)z, where u is the identifier of a consumer and 0 <= z <= 10000 is the value ofc max(u). All input numbers are integers. Except the (u,v)z triplets and the (u)z doublets, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.OutputFor each data set from the input, the program prints on the standard output the maximum amount of power that can be consumed in the corresponding network. Each result has an integral value and is printed from the beginning of a separate line. Sample Input2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)207 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7 (3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5(0)5 (1)2 (3)2 (4)1 (5)4Sample Output156HintThe sample input contains two data sets. The first data set encodes a network with 2 nodes, power station 0 with pmax(0)=15 and consumer 1 with cmax(1)=20, and 2 power transport lines with lmax(0,1)=20 and lmax(1,0)=10. The maximum value of Con is 15. The second data set encodes the network from figure 1.SourceSoutheastern Europe 20032426:ACM Computer FactoryTime Limit: 1000MS Memory Limit: 65536KTotal Submissions: 3986 Accepted: 1325 Special Judge DescriptionAs you know, all the computers used for ACM contests must be identical, so the participants compete on equal terms. That is why all these computers are historically produced at the same factory.Every ACM computer consists of P parts. When all these parts are present, the computer is ready and can be shipped to one of the numerous ACM contests.Computer manufacturing is fully automated by using N various machines. Each machine removes some parts from a half-finished computer and adds some new parts (removing of parts is sometimes necessary as the parts cannot be added to a computer in arbitrary order). Each machine is described by its performance (measured in computers per hour), input and output specification.Input specification describes which parts must be present in a half-finished computer for the machine to be able to operate on it. The specification is a set of P numbers 0, 1 or 2 (one number for each part), where 0 means that corresponding part must not be present, 1 — the part is required, 2 — presence of the part doesn't matter.Output specification describes the result of the operation, and is a set of P numbers 0 or 1, where 0 means that the part is absent, 1 — the part is present.The machines are connected by very fast production lines so that delivery time is negligibly small compared to production time.After many years of operation the overall performance of the ACM Computer Factory became insufficient for satisfying the growing contest needs. That is why ACM directorate decided to upgrade the factory.As different machines were installed in different time periods, they were often not optimally connected to the existing factory machines. It was noted that the easiest way to upgrade the factory is to rearrange production lines. ACM directorate decided to entrust you with solving this problem.InputInput file contains integers P N, then N descriptions of the machines. The description of i th machine is represented as by 2 P + 1 integers Q i S i,1Si,2...S i,P D i,1D i,2...D i,P, where Q i specifies performance, S i,j— input specification for part j, D i,k— output specification for part k.Constraints1 ≤ P≤ 10, 1 ≤ N ≤ 50, 1 ≤ Q i≤ 10000OutputOutput the maximum possible overall performance, then M— number of connections that must be made, then M descriptions of the connections. Each connection between machines A and B must be described by three positive numbers A B W, where W is the number of computers delivered from A to B per hour.If several solutions exist, output any of them.Sample InputSample input 13 415 0 0 0 0 1 010 0 0 0 0 1 130 0 1 2 1 1 13 0 2 1 1 1 1Sample input 23 55 0 0 0 0 1 0100 0 1 0 1 0 13 0 1 0 1 1 01 1 0 1 1 1 0300 1 1 2 1 1 1Sample input 32 2100 0 0 1 0200 0 1 1 1Sample OutputSample output 125 21 3 152 3 10Sample output 24 51 3 33 5 31 2 12 4 14 5 1Sample output 30 0HintBold texts appearing in the sample sections are informative and do not form part of the actual data.SourceNortheastern Europe 2005, Far-Eastern Subregion。