胡克定律的应用PPT课件
- 格式:ppt
- 大小:799.00 KB
- 文档页数:24









轴向拉伸与压缩 78第5章5.3 轴向拉(压)杆横截面上的变形直杆在轴向拉伸或压缩时,将引起轴向尺寸的伸长或缩短,以及横向尺寸的缩短或伸长。
5.3.1 纵向变形与横向变形设等直杆在变形前原长为l ,横向尺寸为d;受轴向拉力F 的作用,杆的长度变为l 1,横向尺寸变为d 1,如图5-9所示。
杆件沿轴向的变形称为纵向变形,沿横向的变形称为横向变形。
下面分别予以讨论。
图5-9 轴向拉(压)杆横截面变形示意图(1)纵向变形。
Δl = l 1 − lΔl 为纵向变形,它反映了杆件总的纵向变形量,但不能反映变形的程度。
为此用纵向变形量除以总长度,即l l ε∆= (5.3) 称ε 为纵向线应变,简称线应变,它反映了杆件纵向变形的程度。
ε 是一个量纲唯一的量,它的正负号规定与Δl 相同,拉伸时为正,压缩时为负。
(2)横向变形。
Δd = d 1 − dΔd 为横向变形,其相应的横向应变记为ε′,即'ε=d d ∆ (5.4)5.3.2 胡克定律对于一般工程材料制成的轴向受拉(压)杆,实验证明:当杆所受的外力未超过材料的某一极限值时(下节将介绍这一极限值就是材料的比例极限),杆的伸长(缩短)Δl 与杆所受的外力F 及杆的原长l 成正比,而与其横截面积A 成反比,即5.3轴向拉(压)杆横截面上的变形79 E σε=或E σε= (5.5)这是胡克定律,式中的比例常数E 称为弹性模量。
它表示材料在拉伸(压缩)时抵抗弹性变形的能力。
其值随材料而异,由实验测定。
单位是Pa (MPa 或GPa )。
实验还表明,当应力不超过比例极限时,横向线应变与轴向线应变成正比,但符号相反,即 'ε=µε−(5.6) 式中,µ 称为泊松比,是无量纲量,它和弹性模量E 一样,都是材料的固有弹性常数。
若将式N F A σ=和l lε∆=代入式E σε=,可得到胡克定律的另一中形式 1N F l EA ∆= (5.7)式中的EA 称为抗拉(压)刚度。
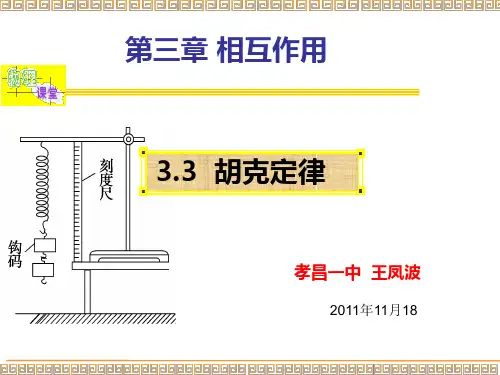
高中物理:胡克定律的应用[探究导入]如图,利用钩码和刻度尺探究弹簧弹力与弹簧伸长量的关系.(1)仔细观察分别挂上一个砝码、两个砝码、三个砝码时弹簧的伸长量记录的数据表格,发现什么规律?提示:Δx3=3Δx121(2)那么弹簧的弹力和砝码的重力有什么关系?提示:根据二力平衡可知两者大小相等.(3)由此我们可以得出什么样的结论?提示:在弹性限度内,弹性体的弹力和弹性体伸长(或缩短)的长度成正比.1.应用胡克定律的四个关键(1)弹簧发生形变时必须在弹性限度内.(2)x 是弹簧的形变量,不是弹簧的原长,也不是弹簧形变后的长度.(3)其F x 图像为一条经过原点的倾斜直线,图像斜率表示弹簧的劲度系数.同一根弹簧,劲度系数不变.(4)一个有用的推论:ΔF =k Δx .推导:F 1=kx 1,F 2=kx 2,故ΔF =F 2-F 1=kx 2-kx 1=k Δx .因此,弹簧弹力的变化量ΔF 与形变量的变化量Δx也成正比关系.2.计算弹力大小的两种方法(1)公式法:利用公式F =kx 计算,适用于弹簧、橡皮筋等物体弹力的计算.(2)二力平衡法:若物体处于静止状态,物体所受弹力与物体所受的其他力应为平衡力,可根据其他力的大小确定弹力的大小.[易错提醒](1)应用胡克定律无论是计算弹簧的弹力大小还是判断弹簧的弹力方向,都应注意弹簧是被拉伸还是被压缩.(2)计算时注意F 、k 、x 单位要统一到N 、N/m 、m ,其中x 为形变量而不是弹簧长度.[典例3] 一根轻弹簧,当它受到10 N 的拉力时长度为12 cm ,当它受到25 N 的拉力时长度为15 cm ,问弹簧不受力时的自然长度为多少?该弹簧的劲度系数为多少?[思路点拨][解析] 设弹簧的原长为l 0,由题意知,F 1=10 N ,l 1=12 cm ;F 2=25 N ,l 2=15 cm. 法一:根据胡克定律有F 1=k (l 1-l 0),F 2=k (l 2-l 0) 两式相比可得F 1F 2=l 1-l 0l 2-l 0代入数据可得l 0=10 cmk =F 1x =F 1l 1-l 0=10(12-10)×10-2N /m =500 N/m. 法二:根据ΔF =k Δx 可得k =ΔF Δx =F 2-F 1l 2-l 1=25-10(15-12)×10-2N /m =500 N/m. 又根据F 1=k (l 1-l 0)可得l 0=l 1-F 1k =0.12 m -10500m =0.1 m =10 cm. [答案] 10 cm 500 N/m[规律总结]胡克定律F =kx 也适用于弹性绳、橡皮筋等产生的弹力的计算,只是它们只能产生拉伸弹力,不能产生压缩弹力.具体问题中要根据题意判断胡克定律是否适用.3.如图所示,轻弹簧的两端各受100 N 拉力F 作用,弹簧平衡时伸长了10 cm(在弹性限度内),那么下列说法中正确的是( )A .该弹簧的劲度系数k =10 N/mB .该弹簧的劲度系数k =1 000 N/mC .该弹簧的劲度系数k =2 000 N/mD .根据公式k =F x,弹簧的劲度系数k 会随弹簧弹力F 的增大而增大 解析:根据胡克定律F =kx 得,弹簧的劲度系数:k =F x =1000.1N /m =1 000 N/m ,故A 、C 错误,B 正确;弹簧的伸长与受到的拉力成正比,弹簧的劲度系数k 与弹簧弹力F 的变化无关,与弹簧本身有关,故D 错误.答案:B。