下载文档原格式
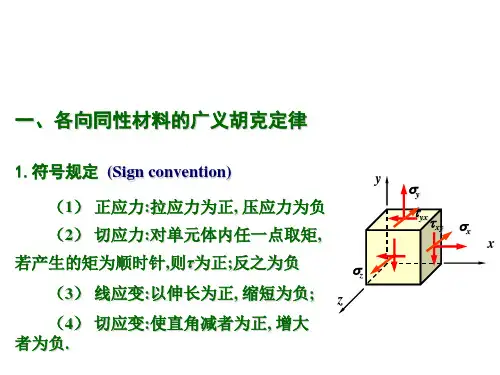
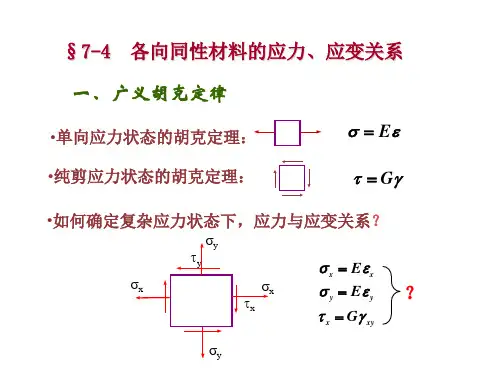
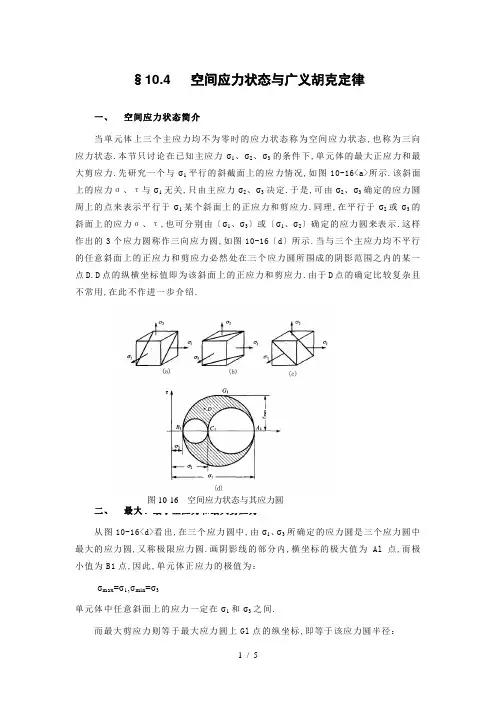
§10.4 空间应力状态与广义胡克定律一、空间应力状态简介当单元体上三个主应力均不为零时的应力状态称为空间应力状态,也称为三向应力状态.本节只讨论在已知主应力σ1、σ2、σ3的条件下,单元体的最大正应力和最大剪应力.先研究一个与σ1平行的斜截面上的应力情况,如图10-16<a>所示.该斜面上的应力σ、τ与σ1无关,只由主应力σ2、σ3决定.于是,可由σ2、σ3确定的应力圆周上的点来表示平行于σ1某个斜面上的正应力和剪应力.同理,在平行于σ2或σ3的斜面上的应力σ、τ,也可分别由〔σ1、σ3〕或〔σ1、σ2〕确定的应力圆来表示.这样作出的3个应力圆称作三向应力圆,如图10-16〔d〕所示.当与三个主应力均不平行的任意斜面上的正应力和剪应力必然处在三个应力圆所围成的阴影范围之内的某一点D.D点的纵横坐标值即为该斜面上的正应力和剪应力.由于D点的确定比较复杂且不常用,在此不作进一步介绍.图10-16 空间应力状态与其应力圆二、最大、最小正应力和最大剪应力从图10-16<d>看出,在三个应力圆中,由σ1、σ3所确定的应力圆是三个应力圆中最大的应力圆,又称极限应力圆.画阴影线的部分内,横坐标的极大值为Al点,而极小值为B1点,因此,单元体正应力的极值为：σmax=σ1,σmin=σ3单元体中任意斜面上的应力一定在σ1和σ3之间.而最大剪应力则等于最大应力圆上Gl点的纵坐标,即等于该应力圆半径：Gl 点在由σ1和σ3所确定的圆周上,此圆周上各点的纵横坐标就是与σ2轴平行的一组斜截面上的应力,所以单元体的最大剪应力所在的平面与σ2轴平行,且与σ1和σ3主平面交450.三、广义胡克定律在研究单向拉伸与压缩时,已经知道了在线弹性范围内,应力与应变成线性关系,满足胡克定律 E σε= 〔a 〕此外,轴向变形还将引起横向尺寸的变化,横向线应变根据材料的泊松比可得出：'E σεμεμ=-=- 〔b 〕在纯剪切的情况下,根据实验结果,在剪应力不超过剪切比例极限时,剪应力和剪应变之间的关系服从剪切胡克定律,即G τγ= 或 G τγ= 〔c 〕对于复杂受力情况,描述物体一点的应力状态,通常需要9个应力分量,如图10.1所示.根据剪应力互等定律,τxy =－τyx ,τxz =－τzx ,τyz =－τzy ,因而,在这9个应力分量中只有6个是独立的.这种情况可以看成是三组单向应力〔图10-17〕和三组纯剪切的组合.对于各向同性材料,在线弹性范围内,处于小变形时,线应变只与正应力有关,与剪应力无关；而剪应变只与剪应力有关,与正应力无关,并且剪应力只能引起与其相对应的剪应变分量的改变,而不会影响其它方向上的剪应变.因此,求线应变时,可不考虑剪应力的影响,求剪应变时不考虑正应力的影响.于是只要利用〔a 〕、〔b 〕、〔c 〕三式求出与各个应力分量对应的应变分量,然后进行叠加即可.图10-17 应力分解如在正应力σx 单独作用时<图10-17<b>>,单元体在x 方向的线应变xxx E σε=；在σy 单独作用时<图10-17<c>>,单元体在x 方向的线应变为：yxy E σεμ=-；在σz 单独作用时<图10-17 <d>>,单元体在x 方向的线应变为zxz E σεμ=-；在σx 、σy 、σz 共同作用下,单元体在x 方向的线应变为：同理,可求出单元体在y 和z 方向的线应变εy 和εz.最后得 1()y y z x E εσμσσ=-+⎡⎤⎣⎦ 〔10-9〕对于剪应变与剪应力之间,由于剪应变只与剪应力有关,并且剪应力只能引起与其相对应的剪应变分量的改变,而不会影响其它方向上的剪应变.因而仍然是〔c 〕式所表示的关系.这样,在xy 、yz 、zx 三个面内的剪应变分别是12(1)yz yz yz G E μγττ+== 〔10-10〕公式〔10-9〕和〔10-10〕就是三向应力状态时的广义胡克定律.当单元体的六个面是主平面时,使x 、y 、z 的方向分别与主应力σ1、σ2、σ3的方向一致,这时有广义胡克定律化为：[]22311()E εσμσσ=-+ 〔10-11〕ε1、ε2、ε3方向分别与主应力σ1、σ2、σ3的方向一致,称为一点处的主应变.三个主应变按代数值的大小排列,ε1 ≥ ε2 ≥ε3,其中,ε1和ε3分别是该点处沿各方向线应变的最大值和最小值.四、 体积应变单位体积的改变称为体积应变〔体应变〕.图10-18所示的主单元体,边长分别是dx 、dy 和dz.在3个互相垂直的面上有主应力σ1、σ2和σ3.单元体变形前的体积为: v = dxdydz ;变形后的体积为：v 1=〔dx +ε1dx><dy +ε2dy><dz+ε3dz>则体积应变为：略去高阶微量,得 123θεεε=++ 〔10-12〕将广义胡克定律式<10-11>代入上式,得到以应力表示的体积应变图10-18 主应力单12312312()E μθεεεσσσ-=++=++ 〔10-13〕令 1231()3m σσσσ=++ 〔10-14〕则 3(12)m m E K μσσθ-== 〔10-15〕式中：3(12)E K μ=-称为体积弹性模量,σm 称为平均主应力.公式〔10-15〕表明,体积应变θ与平均主应力σm 成正比,即体积胡克定律.单位体积的体积改变只与三个主应力之和有关,至于三个主应力之间的比例对体积应变没有影响.若将图10-19〔a 〕中所示单元体分解为〔b 〕和〔c 〕两种情况的叠加,在〔c 〕图中,由于各面上的主应力为平均主应力,该单元体各边长按相同比例伸长或缩短,所以单元体只发生体积改变而不发生形状改变.在图〔b 〕中,三个主应力之和为零,由式〔10-13〕可得其体积应变θ也为零,表明该单元体只发生形状改变而不发生体积改变.由此可知,图〔a 〕所示的单元体的变形将同时包括体积改变和形状改变.五、 复杂应力状态下的弹性变形比能弹性变形比能是指物体在外力作用处于弹性状态下,在单位体积内储存的变形能.在单向应力状态下,当应力σ与应变ε满足线性关系时,根据外力功和应变能在数值上相等的关系,导出变形比能的计算公式为图10-19 单元体应力的组合在复杂应力状态下的单元体的变形比能为将将广义胡克定律<10.11>式代入上式,经过整理后得出：22212312233112()2E σσσμσσσσσσ⎡⎤=++-++⎣⎦ 〔10-16〕 式〔10-16〕就是在复杂应力状态下杆件的弹性变形比能计算公式.由于单元体的变形包括体积改变和形状改变,所以变形比能也可以看成由体积改变比能和形状改变比能这两部分的组合.式中：u θ为体积改变比能,d u 为形状改变比能.对于图〔10-19〔c 〕〕中的单元体,各面上的正应力为：1231()3m σσσσ==++,将σm 代入式〔10-16〕得体积改变比能： 212312()6E μσσσ-=++ 〔10-17〕形状改变比能：2221223311[()()()]6E μσσσσσσ+=-+-+- 〔10-18〕 例10-7 如图10-20所示钢梁,在梁的A 点处测得线应变640010,x ε-=⨯612010,y ε-=-⨯ 试求：A 点处沿x 、y 方向的正应力和z 方向的线应变.已知弹性模量E=200GPa,泊松比μ=0.3.图10-20 钢梁上某点A 的位置解：因为A 点的单元体上σz=0,该单元体处于平面应力状态,将εx 、εy 、E 、μ代入公式〔10-9〕,得解得：σx=80MPa,σy=0再由。
