当前位置：文档之家 › 受力图 汇交力系例题

受力图 汇交力系例题

  • 格式：ppt
  • 大小：756.00 KB
  • 文档页数：28

下载文档原格式

  / 28

合集下载

汇交力系例题

汇交力系例题


C
Y P TBD cos cos TBC cos cos 0
Z RA TBD sin TBC sin 0
联立解得
TBC 735 N
TBD 1094 N
RA 1500 N
p.4
例题
例题
例4.已知四根绳索AB、BC、BD、DE相互联接如图所示， DB保持水平，DE和BC分别与水平和铅垂线的夹角均
A
45o
0.8m
CB
0.4m
y
SC
A
45o C
RA
B x
E
P
EB BC 0.4m tg EB 0.4 1
AB 1.2 3 (2) 列出平衡方程；
X 0, RA cos Sc cos 45 0
Y 0,RA sin Sc sin 45 P 0
(3) 求未知力；
P
2
Sc sin 45 cos45tg
C EA
D
B -
y TDB D + x
y
TBE
TBC
B
TBD
x
P
TDA
P
SAB
解: (1) 研究D点，画受力图；
(2) 列出平衡方程并求解；
X 0,TDB cos( ) TDA cos( ) 0
Y 0,TDB sin( ) TDA sin( ) P 0
TDB
NA
O
O’与 O为矩形OAO’B的两个顶点，
O’ B
力的作用线既通过O’点也通过O点。
NB
由几何关系得
P A
90 2
NA
O
OA Lsin
p.6
例题
例题
例6. 铰接四连杆机构CABD的CD边固定。在铰链A上作用一 力Q，BAQ=45。在铰链B上作用一力R，ABR=30，
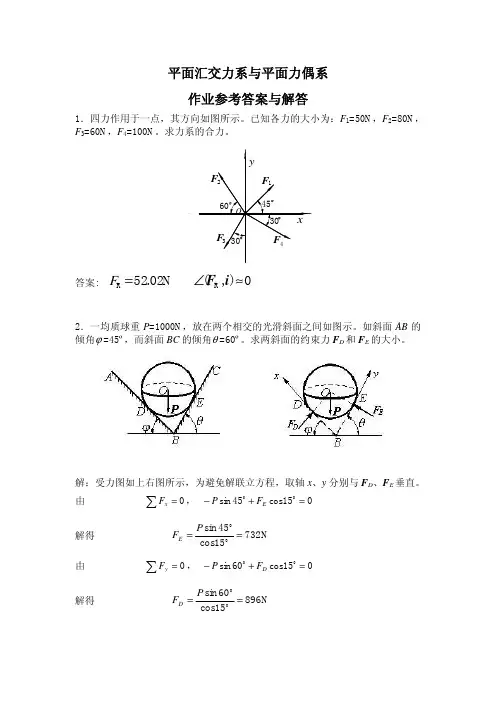
平面汇交力系参考解答

平面汇交力系参考解答

M , a sin θ 答案： M FE = FF = , h FCD = CD 是二力杆 , FCD 的方向沿杆的轴线。
方向水平
即： FAC = FBC = 9.56kN ,
FCAD = 0.794kN
4．均质杆 AB 长 l，置于销子 C 与铅垂面间，如图所示。不计摩擦力，求平衡时 杆与铅垂线间的夹角θ 。
解：由三力平衡汇交定理，杆 AB 所受主动力和约束力的作用线汇交于点 O，如 右上图所示。根据几何关系有 l AO AC a AD = = = = 2 2 sin θ sin θ sin 3 θ 解得： θ = arcsin 3
P sin 60 FD = = 896 N cos15
3．以吊斗运物过河，吊斗系用小车 C 挂在钢丝绳 AB 上，如图所示。如欲将小 车拉向左岸，则利用一跨过滑车 A 而绕在绞盘 D 上的绳索 C AD；如欲将小车拉 向右岸，则可利用一跨过滑车 B 而绕在铰盘 E 上的绳索 C BE。A、B 两点在同一 水平线上，距离 AB=100m，钢索 ACB 长 102m，吊斗重 5kN。如略去钢索和绳 子的重量以及小车 C 沿钢索的摩擦， 求当 AC=20m 时绳子 C AD 和钢索 A C B 的 张力。
FCAD = FT2 。
取小车 C 为研究对象，受力图见右上图， FAC = FBC = FT1 , 由 由
Fς Fξ
= 0, = 0,
FT1 sin(ϕ + θ ) − P cos θ = 0
FT1 = 9.56 kN FT2 = 0.794 kN
FT1 cosϕ − ( FT1 + FT2 ) cos θ = 0
F
y
= 0 , F21 cos 30 + F31 cos 30 − P = 0 , F21 = F31 =
工程力学 03汇交力系-19(例题)

工程力学 03汇交力系-19(例题)


理论力学 Theoretical Mechanics
解： 1. 取杆AB与重物为研究对象，受力分析如图。 与重物为研究对象，受力分析如图。 其侧视图为
z E C F
30o
D
F2
B
z E F
30o
F1
B
F1
α
FA
A
x
G
y
α
FA
A
G
y
理论力学 Theoretical Mechanics
z E F
30o
2
理论力学 Theoretical Mechanics
因为α很小，所以可取
tgα ≈ α
G 800 N = 80kN F TBA = G ctg α = 2 = 2 tg α 0.1
2
显然，拔力为
F
' TBA
= F TBA = 80kN
江苏工业学院机械系力学教研室
理论力学 Theoretical Mechanics
（4）由几何关系得： O =EA= 24 cm 由几何关系得： E
A
P
A
P
α
24
D E tgϕ = = 0.25 O E
C O B D
(a)
O
α ϕ
B
FB
E
6
ϕ = arctg0.25 =14°2'
FD
D
(b)
由力三角形可得： 由力三角形可得： = sin(180°−α−ϕ) P F B
sinϕ
P
J
解得
Fcosθ ⋅ yB −Fsinθ ⋅ xB FD = C l
江苏工业学院机械系力学教研室
理论力学 Theoretical Mechanics
平面力系-平面汇交力系的简化与平衡方程(常用版)

平面力系-平面汇交力系的简化与平衡方程(常用版)

平面力系-平面汇交力系的简化与平衡方程（常用版）(可以直接使用，可编辑完整版资料，欢迎下载）第2章平面力系192.1 平面汇交力系的简化与平衡方程 (19)2.2 力对点之矩合力矩定理 (24)2.3 力偶及其性质 (27)2.4 平面力偶系的合成与平衡方程 (30)2.5 平面一般力系的简化与平衡方程 (32)2.6 物体系统的平衡 (40)*附录Ⅱ：机械应用实例 (49)第2章平面力系本章主要介绍平面力系的简化与平衡问题，平面状态下物系平衡问题的解法。

按照力系中各力的作用线是否在同一平面内，可将力系分为平面力系和空间力系。

若各力作用线都在同一平面内并汇交于一点，则此力系称为平面汇交力系。

按照由特殊到一般的认识规律，我们先研究平面汇交力系的简化与平衡规律。

2.1 平面汇交力系的简化与平衡方程2.1.1 概述设刚体上作用有一个平面汇交力系F1、F2、…、F n，各力汇交于A点（图2-1a）。

根据力的可传性，可将这些力沿其作用线移到A点，从而得到一个平面共点力系（图2-1b）。

故平面汇交力系可简化为平面共点力系。

a ）b ）图2-1连续应用力的平行四边形法则，可将平面共点力系合成为一个力。

在图2-1b 中，先合成力F 1与F 2（图中未画出力平行四边形），可得力F R1，即 F R1＝F 1+ F 2；再将F R1与F 3合成为力F R2，即F R2＝F R1+ F 3；依此类推，最后可得F R ＝F 1+ F 2+…+ F n ＝∑F i （2-1）式中 F R 即是该力系的合力。

故平面汇交力系的合成结果是一个合力，合力的作用线通过汇交点，其大小和方向由力系中各力的矢量和确定。

因合力与力系等效，故平面汇交力系的平衡条件是该力系的合力为零。

2.1.2力在坐标轴上的投影过F 两端向坐标轴引垂线（图2-2）得垂足a 、b 、a'、b'。

线段ab 和a'b'分别为F 在x 轴和y轴上投影的大小，投影的正负号规定为：从a 到b （或从a'到b'）的指向与坐标轴正向相同为正，相反为负。

理论力学-平面汇交力系

理论力学-平面汇交力系

第一篇
静力学
第二章
平面力系
第二章
平面力系
主要内容
1. 2. 3. 4. 5. 平面汇交力系的合成与平衡 平面力偶系的合成与平衡 平面任意力系的合成与平衡 静定与超静定 ·物系的平衡 平面简单桁架的内力计算
第二章
平面力系
§2-1 平面汇交力系
§2-1 平面汇交力系
何谓平面汇交力系？
作用在刚体上的力都在同一平面上，
C B
D y
二力杆
Fx 0, Fy 0,
FA cos FC cos 45 0
FA
A
E
FA sin FC sin 45 F 0

C
F
45o
B x
5. 解得： FA =22.4kN FC =28.3kN
FC
§2-1 平面汇交力系
解题技巧及说明
1、通常，对于只受三个力作用而平衡的物体，且角 度特殊时用几何法比较简便。- 解力三角形 2、对于受多个力作用平衡的物体，均用解析法。 3、投影轴的选择原则：与未知力垂直或平行，最好 使每个方程中只有一个未知数。 4、解析法解题时，如果力的指向不能确定，可任意 假定，如求出负值，说明力的实际方向与假设方 向相反。 如：对于二力构件，可先预先设为拉力。
— 力多边形
含义：平面汇交力系的合力等于各分力的矢量和， 合力的作用线通过各分力的汇交点。
§2-1 平面汇交力系 2、平面汇交力系平衡的几何条件 平面汇交力系平衡的充要条件是：
FR = 0 , 即
F2 F1
F3
F5 = FR
F = 0
i
相应地，从几何角度上讲，如何？ 平面汇交力系平衡的充要条件是：
受力图汇交力系例题

受力图汇交力系例题


方向：平行于Q、P且指向一致
作用点：C处
拟定C点，由合力距定理
mB (R )mB (Q ) 又 R P Q
AB AC CB代入
RCB Q AB 整理得 AC P
CB Q
②两个反向平行力旳合力 大小：R=Q-P
方向：平行于Q、P且与较大旳相同
作用点：C处
（推导同上）
CB Q CA P
性质2：力偶对其所在平面内任一点旳矩恒等于力偶矩，而
①力偶能够在其作用面内任 不变，能够任意变化力偶中力
意移动，而不影响它对刚体 旳大小和相应力偶臂旳长短，
旳作用效应。
而不变化它对刚体旳作用效应。
2、力偶系旳合成与平衡
平面力偶系:作用在物体同一平面旳许多力偶叫平面力偶系 设有两个力偶
d
d
m1 F1d1;
m2 F2d2
又m1 P1d
m2 P2d
Fd mO (R)
因为O点是任取旳
m F d + —
阐明：① m是代数量，有+、-； ②F、 d 都不独立，只有力偶矩 m F d 是独立量； ③m旳值m=±2⊿ABC ； ④单位：N• m
性质3：平面力偶等效定理 作用在同一平面内旳两个力偶，只要它旳力偶矩旳大小相等，
转向相同，则该两个力偶彼此等效。 [证] 设物体旳某一平面 上作用一力偶(F,F') 现沿力偶臂AB方向 加一对平衡力(Q,Q'), 再将Q,F合成R，
与矩心旳位置无关，所以力偶对刚体旳效应用力偶矩度量。
力偶无合力 R=F'-F=0
CB F ' 1 CB CA
CA F
若CB CB d成立,必有CB
d 合力的作用点在无限远处
第二章 汇交力系

第二章 汇交力系


同理： FRy F1y F2 y F3y Fy
§1 汇交力系的合成
5、汇交力系合成的解析法
应用合力投影定理求出力系合力的投影后，可用下式 求出合力的大小和方向： 合力的大小：
FR FR2x FR2y FR2z ( Fx )2 ( Fy )2 ( Fz )2
合力FR 的方向余弦：
汇交力系的合成 几何法(矢量法) 解析法(投影法)
汇交力系的平衡条件 几何法(矢量法) 解析法(投影法)
§1 汇交力系的合成
一、力的可传性
F
公理三：加减平衡力系原理 在刚体上增加或减去
一组平衡力系，不会改变 原力系对刚体的作用效应
F’ F”
F A
B
F
A
B
若{P1, P2 ,L , Pm} {0} 则 {F1, F2, , Fn}
例2-3：圆柱重G=500N，搁在光滑墙面与夹板间， 板与墙面夹角为60°，用解析法求：圆柱给墙面和 夹板的压力。
解：1.以圆柱为研究对象，画受力图；
FA
O
G
FB
O
AG
60° B
例2-3：圆柱重G=500N，搁在光滑墙面与夹板间，
板与墙面夹角为60°，用解析法求：圆柱给墙面和
夹板的压力。
解：1.以圆柱为研究对象，画受力图：
Fx + Fy = F
| F | = (Fx)2 + (Fy)2 x
= (Fx)2 + (Fy)2
α = atan (Fy /Fx)
§1 汇交力系的合成
三、汇交力系合成的解析法(投影法)
可见： 力F在垂直坐标轴上的投影分量与沿轴分解的分 力大小相等；力F在相互不垂直的轴上的投影分 量与沿轴分解的分力大小是不相等的。 力在任一轴上的投影大小都不大于力的大小；而 分力的大小却不一定都小于合力大小。 力在任一轴上的投影可求，力沿一轴的分量不可 定。
汇交力系

汇交力系

＝20kN，不计刚架自重。用几何法求支座A、D处的约束反力。
解 (1) 选平面刚架为研究对象，按比例画出其分离体图。
(2) 对刚架进行受力分析，并画出其受力图，如图 b) 所示。
刚架上作用有水平力F，辊轴支座D的反力FD。根据三力平衡汇交 定理，力F和FD交于C点，所以固定铰支座处的反力FA，必沿A、
200 0.5 300 0.866 100 0.707 250 0.707 112 . 3 N
合力：
夹角：
FR
2 2 FRx FRy 171.3N
FRx FR , i arccos arccos( 0.7548 ) 40.99 o FR
力。梁的自重不计。
F
A C 60º B 30º 60º 60º
a
a
30º
30º
解：(1) 取梁AB 作为研究对象。 (2) 画出受力图。 (3) 应用平衡条件画出F、FA 和FB 的闭合力三角形。 (4) 解出：FA = Fcos30 = 17.3 kN，FB = Psin30 = 10 kN
[例] 平面刚架ABCD在B点作用一水平力F，如图所示。已知F
例题 已知 P = 20 kN，求平衡时杆AB 和 BC所受的力 解： 取节点 B 为研究对象，AB 、BC 都是二力杆
A D
60 0
画受力图 建立坐标系如图 B 由平衡方程：
F
x
0
30
0
FBA F1 cos 600 F2 cos300 0
C
F
P
y
30 0
y
0
FBC F1 cos300 F2 cos 600 0
§2-1 汇交力系合成与平衡的几何法
第二章 平面力系

第二章 平面力系


FR F1 F2 Fn Fi
i 1
n
力FR对刚体的作用与原力系对该刚体的作用等效。所以 称此力为汇交力系的合力。
如力系中各力作用线均沿同一直线，则此力系为共线力系， 它是平面汇交力系的特殊情况。显然力系的合力大小和方向 取决于各分力的代数和，即 n
FR Fi
i 1
24
静力学
例题 1-5
平面力系
合力的大小：
2 Rx 2 Ry
FR F F 171.3 N
合力与轴x，y夹角的方向余弦为：
FRx cos( FR , i ) 0.754 FR
F2
y
F1
60
O
45
30
cos( FR , j )
FRy FR
45
x
F4
0.656
F3
平面力系
Fx Fx1 Fx 2 Fxn Fxi i 1 n Fy Fy1 Fy 2 Fyn Fyi i 1
n
合力矢FR的大小和方向余弦为
FR Fx2 Fy2 ( Fxi ) 2 ( Fyi ) 2
B
D
钢丝绳的另一端绕在铰车D上。 杆AB与BC铰接，并以铰链A，C 与墙连接。如两杆与滑轮的自重
4 .由力三角形图c可得：
I
F
q
FD

J
K
FB
(c)
sin 180 q FB F 750 N sin
11
静力学
例题 1-2
平面力系
水平梁AB中点C作用着力F，其大小等于2 kN，方向与梁
的轴线成60º 角，支承情况如图a 所示，试求固定铰链支座A和活动铰链支座B的约束源自。梁的自重不计。3，
第2章(汇交力系)

第2章(汇交力系)


合力FR 的大小 合力
FR = ( ∑ Fx )2 + ( ∑ Fy )2 = (8.33)2 + ( −0.5)2 = 8.345kN
合力F 合力 R 的方向
∑F cos α =
FR
∴ α = 3.6o
x
= arccos
8.33 = 0.998 8.345
端与固定铰链联结， 例：边长为a 的直角弯杆 边长为 的直角弯杆ABC 的A 端与固定铰链联结，C 端与杆 CD 用销钉联结，杆CD 与水平线的夹角为 o ，不计杆自重，沿BC 方 用销钉联结， 与水平线的夹角为60 不计杆自重， 向作用已知力F 向作用已知力 = 60N。试求 、C 两点的约束力。 。试求A、 两点的约束力。 以直角弯杆ABC 为研究对象，受 为研究对象， 解: 以直角弯杆 力图与坐标系如图所示。 力图与坐标系如图所示。建立平衡方程
F3 F4 FR FRx
x
FR = FRx i + FRy j + FRz k = ∑ Fx i + ∑ Fy j + ∑ Fz k
合力F 合力 R 的大小 FR = ( ∑ Fx )2 + ( ∑ Fy )2 + ( ∑ Fz )2 合力FR 的方向 合力
R
∑F cos( F ，i ) =
cos( FR，j ) = F
二、汇交力系平衡的几何条件
汇交力系平衡的充分与必要条件是力系的合力 等于零， 等于零，即
FR = F1 + F2 + ⋅ ⋅ ⋅ + Fn = ∑ F = 0
汇交力系的平衡条件 表示为几何形式是最后一 个力的终点与第一个力的 始点重合， 始点重合，即力的多边形 是自形封闭的。 是自形封闭的。
3-平面力系-汇交力系

3-平面力系-汇交力系


力在轴上的投影等于力的大小乘以力与轴正向之间夹角的余弦.
Fn ab F cos
13
1.力在轴上的投影
补充例题3. F1=F2=F3=F4=100N。求各力在 x 轴上的投影。
300 F1 F2
450
F3 F4
x
F1x = F1sin30o=100×0.5=50N
F2x F2 cos 45 100
FRx
Fx
合力的作用线通过汇交点
19
四、平面汇交力系合成的解析法
补充例题4. 已知 F1 = 100N, F2 =F3 = 70 N, F4 = 90 N,
方向如图所示, 求该力系的合力。
45°
解： 应用解析法（合力投影定理）得：
FRx Fx F1 sin 45 F2 cos30 F3 cos 45 F4 sin 30 F4 30°
5
§2-1 平面汇交力系 一、平面汇交力系合成的几何法、力多边形法则
平面汇交力系可以合成为一个合力，合力大小和方向 由力多边形的封闭边确定，其作用线通过汇交点。合力等 于原力系中所有力的矢量和，即
n
FR F1 F2 Fn Fi i 1
可简写为
FR Fi
n 个力汇交情况
FA

A
注意：列平衡方程时，FA 的指向是以受力图中假定的方向， 若将FA带入解析式计算时仍保留其负号（带入负值）。
正弦定理有
F2
s in

FR1 sin120
得: 25.69
22
§2-1 平面汇交力系
平面汇交力系平衡方程的应用
例题2-1. 已知:F1=130N， F2=100N， F3=80N 。试确定这三个力的合力FR 。

平面汇交力系


只要不平行即可
平面简单力系
平面汇交力系合成与平衡的解析法
2. 解析法解题步骤： 解析法解题步骤： （1）选取研究对象； 选取研究对象； （2）画出研究对象的受力图； 画出研究对象的受力图； （3）合理选取坐标系，列平衡方程求解； 合理选取坐标系，列平衡方程求解； （4）对结果进行必要的分析和讨论。 对结果进行必要的分析和讨论。 几点说明： 几点说明： （1）投影轴常选择与未知力垂直，最好使每个方程中只有一个 投影轴常选择与未知力垂直， 未知数； 未知数； （2）未知力的方向可以先假设，如果求出负值，说明与假设相 未知力的方向可以先假设，如果求出负值， 反。对于二力构件，一般先设为拉力，如果求出负值，说 对于二力构件，一般先设为拉力，如果求出负值， 明物体受压力。 明物体受压力。
引 言
桥梁受有：自身重力、铁轨压力、桥墩作用力、风载等。 桥梁受有：自身重力、铁轨压力、桥墩作用力、风载等。 机身受有：自身重力、旋翼轴的作用力、空气动力等。 机身受有：自身重力、旋翼轴的作用力、空气动力等。 研究内容：刚体在各种力系作用下平衡的一般规律。 研究内容：刚体在各种力系作用下平衡的一般规律。
平面简单力系
平面汇交力系合成与平衡的几何法
结论：平面汇交力系可简化为一合力，其合力的大小与方向由 结论：平面汇交力系可简化为一合力， 力多边形的封闭边来表示，其作用线通过各力的汇交点， 力多边形的封闭边来表示，其作用线通过各力的汇交点， 即合力等于各分力的矢量和（或几何和）。 即合力等于各分力的矢量和（或几何和）。 几点讨论： 几点讨论：
引 言
r r r 的质点上。 设：共点力系 {F ,F ,L,F }作用在质量为 m 的质点上。 1 2 n
i =1 r 结论： 结论：力系中 ∑F 是反映其作用效应的物理量之一 i i =1 r F

工程力学例题

试求: (1)当水平拉力F=5 kN时，碾子对地面和障碍物的压力；
(2)欲将碾子拉过障碍物，水平拉力至少应为多大；
(3)力F沿什么方向拉动碾子最省力，此时力F为多大。
解：1.选碾子为研究对象，受力分析如图b所示。
由已知条件可求得
再由力多边形图c中各矢量的几何关系可得
2.碾子能越过障碍的力学条件是FA=0，得封闭力三角形abc。
My= ∑My=－M2=－80 N·m
Mz= ∑Mz=－M1－M4cos 45o－M5cos 45o=－193.1 N·m
M=Mx2+My2+Mz2= 284.6 N·m
cos (M,i) =MX/M=－0.6786
cos (M,j) =MY/M=－0.2811
cos (M,k) =MZ/M=－0.6786
解：选工件为研究对象
FA= FB
列平衡方程：
∑M= 0，FAl－M1－M2－M3=0
FA= FB=200 N
例题4横梁AB长l，A端用铰链杆支撑，B端为铰支座。梁上受到一力偶的作用，其力偶矩为M，如图所示。不计梁和支杆的自重，求A和B端的约束力。
解：选梁AB为研究对象
FA=FB
列平衡方程：
∑M= 0，M－FAlcos45o= 0
解：取滑轮B为研究对象，忽略滑轮的大小，画受力图。
FT=G列平衡方程：
∑Fx=0－FAB－FT cos30o+ FTcos60o= 0
∑Fy=0FBC－FTcos30o－FTcos60o=0
解方程得:FAB=-0.366G=-7.312KNFBC=1.366G=27.32KN
例题6梯长AB=l，重G=100 N，重心假设在中点C，梯子的上端A靠在光滑的端上，下端B放置在与水平面成40°角的光滑斜坡上，求梯子在自身重力作用下平衡时，两端的约束力以及梯子和水平面的夹角θ。

工程力学课堂习题

图例1，已知： ，求1力系向O点的简化结果；2合力与OA的交点到点O的距离x.3合力作用线方程.
解：（1）主矢
主矩：
（2）求合力及作用线位置
（3）求合力作用线方程：
第三节平面任意力系的平衡条件和平衡方程
一.平面任意力系的平衡方程
平面任意力系平衡的充要条件是：力系的主矢和对任意点的主矩都等于零。
由于：
解：取AB梁，画受力图.
图例3,已知自重 的T形钢架， ，求固定端A的约束力。
总结：从上述例题可看出，选取适当的坐标轴和力矩中心，可以减少每个平衡方程的未知量的数目。在平面任意力系下，矩心应取在多个未知力的交点上，坐标轴尽可能与多的未知力相垂直。如果在例3中，若以方程 ，取代 ，可以直接求得 的值。因此，在计算某些问题时，采用力矩方程比投影方程简单。下面介绍平面任意力系平衡方程的其他两种形式。
其中， ， ，代入方程得：
（2）求拉力的最小值。假设拉力的方向与水平夹角为 ，画受力图。这里我们只求最小拉力，可以不求 ，因此可以选取垂直于 的坐标轴列平衡方程：
解得： ，显然，当 时，拉力最小。
平面力矩
力对刚体的作用使刚体的运动状态发生改变，其中移动效应用力矢来表示，转动效应用力对点之矩度量。
1力对点之矩：代数量，绝对值等于力的大小与力臂的乘积，使物体绕矩心逆时针转动为正，单位
例题1,已知: ,求物块是否静止,摩擦力的大小和方向。
例2，求使物块静止，推力F的大小。
材料力学篇
轴向拉伸和压缩
内力截面法轴力图
扭转
等直圆杆扭转时的应力
AC段
BD段
平面汇交力系合成与平衡的解析法
1解析法：设有n个力组成的平面汇交力系作用于一个刚体上，建立直角坐标系，则此汇交力系的合力的解析表达式为

汇交力系例题


= 0 S AB =
SAB’
y
再以压板为研究对象并分析受力: 再以压板为研究对象并分析受力 SAB’, Q, N
B Q
N
x
∑ Y = Q S ′AB cos α = 0
∴Q =
P ctg α 2
讨论：P力一定， 越小，压紧力Q越大。 讨论 P力一定，α 越小，压紧力Q越大。
p.3 p.3例题 Nhomakorabea例
题
1.12 = 41° 1.29
(3) 画出合力 ； 画出合力R；
p.10 p.10
例
题
例
题
AB与 构成， 例10.图示一管道支架，由杆AB与CD构成，管道通过拉杆悬挂 .图示一管道支架，由杆AB CD构成 在水平杆AB AB的 每个支架负担的管道重为2KN 2KN， 在水平杆AB的B端，每个支架负担的管道重为2KN，不计 杆重。求杆CD所受的力及支座A CD所受的力及支座 杆重。求杆CD所受的力及支座A的反力 。
OA
受力分析： 受力分析： P,SOA, SAB 选投影轴列方程： 选投影轴列方程：
A P
x
P SAB
A
α
α
B
∑ Y = SOA cos α + S AB cos α = 0
∑ X = P SOA sin α S AB sin α
选投影轴列方程： 选投影轴列方程
SOA = S AB
P 2 sin α
P
4m
B
C
P
B
C
A
8m
D
A RA
θ
D ND c P ND b
解: (1) 研究刚架；根据三力平衡汇交定理画出受力图； 研究刚架；根据三力平衡汇交定理画出受力图；

汇交力系习题解答

第二章习题解答2—1如图所示，固定在墙壁上的圆环首三条绳索的拉力作用，力F1沿水平方向，力F3沿铅直方向，力F2与水平线成40度角。

三力的大小分别为F1=2000N,F2=2500N,F3=1500N.求三力的合力。

解：图解法解题时，首先要确定比例尺，即每单位长度代表多大的力，这里我们用单位代表500N，三力在圆环的圆心处相交。

如图（b），力系的力多边形如图（c）。

在图上量出OC的长度和L和与水平之间的夹角有。

Fr=L×500=5000Nφ=38°26＇由（c）图的几何关系可见OB=BC,∠BOC=∠BCO=(40°－36°52＇)=1°34＇故合力F r的大小约为Fr＝2F2cos1°34＇=2×2500×0.99963＝4998N与水平方向之间的夹角为φ=38°26＇例：用解析法求圆环受三个力的合力。

解：如图建立坐标，则NF F F F NF F F F y R y x xR 310764279.025********cos 391576604.025********cos 2321=⨯+=︒+===⨯+=︒+==∑∑ 合力的大小NF F F yR xR r 5000310739152222=+=+=合力与X 轴之间的夹角为 '283850003915cos arccos1︒===-R Rx F F α2—2 物体重P=20 kN ，用绳子挂在子架的滑轮B 上，绳子的另一端杰在绞车D 上，如图所示。

转动绞车，物体便能升起。

，A 、B 、C 处均为光滑铰链连接。

钢丝绳、杆和滑轮的自重不计，并忽略摩擦和滑轮的大小。

试求平衡时杆AB 和BC 所受得力。

解：该题与例题基本相同1、确定研究对象。

系统中AB,BC 为二力杆，设AB 受拉力，BC 受压力，以各力汇交的滑轮为研究对象。

2、画滑轮的受力图如图（C ）建立坐标，列平衡方程（坐标轴要尽量和未知的约束力的方向一致或垂直）030cos 60cos 0030cos 60cos ,0=+︒+︒-==︒-︒+=∑∑P P F F F P F F BC y BC AB x4、解方程，得kN F kNF BC BA 64.747.54==1、 答2—3 火箭沿与水平面成θ=25°角的方向作匀速直线运动，如图所示。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

此题也可用力多边形方法用比例尺去量。 几何法解题步骤：①选研究对象；②作出受力图；
③作力多边形，选择适当的比例尺；
④求出未知数
几何法解题不足： ①精度不够，误差大 ②作图要求精度高；
③不能表达各个量之间的函数关系。
下面我们研究平面汇交力系合成与平衡的另一种方法：
解析法。
[例] 已知 P=2kN 求SCD , RA
作用点：C处
确定C点，由合力距定理
mB(R)mB(Q) 又 RPQ
RCB QAB ABAC C代 B 入 整理得ACP
CB Q
②两个反向平行力的合力 大小：R=Q-P
方向：平行于Q、P且与较大的相同
作用点：C处
（推导同上）
CB Q CA P
性质2：力偶对其所在平面内任一点的矩恒等于力偶矩，而
与矩心的位置无关，因此力偶对刚体的效应用力偶矩度量。
合 M R A 力 d ( P 1 P 2 ') d P 矩 1 d P 2 'd m 1 m 2
结论:
M m 1m 2 m n nm i
i 1
平面力偶系合成结果还是一个力偶,其力偶矩为各力偶矩
的代数和。
平面力偶系平衡的充要条件是:所有各力偶矩的代数和
等于零。
即
n
mi 0
i1
画受力图应注意的问题
1）、不要漏画力
除重力、电磁力外，物体之间只有通过接触 才有相互机械作用力，要分清研究对象（受
力体）都与周围哪些物体（施力体）相接触，
接触处必有力，力的方向由约束类型而定。
2）、不要多画力
要注意力是物体之间的相互机械作用。因此对 于受力体所受的每一个力，都应能明确地指出 它是哪一个施力体施加的。
解力三角形：
NcoFs
又： co s R 2R (Rh)2R 1 h(2Rh)
N FR h(2Rh)
再研究球，受力如图：
作力三角形
解力三角形：
P N sin
又 si nRR h NN PNsinhF (2R R h)RR h
NB=0时为球 离开地面 P F(Rh)
h(2Rh)
FP
h(2Rh) Rh
[例2] 画出下列各构件的受力图
O
C
E
D
Q
A
B
O
C
E
D
Q
A
B
O
C
E
D
Q
A
B
[例3] 画出下列各构件的受力图
说明：三力平衡必汇交 当三力平行时，在无限 远处汇交，它是一种特 殊情况。
[例4] 尖点问题
应去掉约束
应去掉约束
[例5] 画出下列各构件的受力图
汇交力系例题
[例] 已知压路机碾子重P=20kN, r=60cm, 欲拉过h=8cm的障碍 物。求：在中心作用的水平力F的大小和碾子对障碍物的压力。
m F d + —
说明：① m是代数量，有+、-； ②F、 d 都不独立，只有力偶矩 mFd是独立量； ③m的值m=±2⊿ABC ； ④单位：N• m
性质3：平面力偶等效定理 作用在同一平面内的两个力偶，只要它的力偶矩的大小相等，
转向相同，则该两个力偶彼此等效。 [证] 设物体的某一平面 上作用一力偶(F,F') 现沿力偶臂AB方向 加一对平衡力(Q,Q'), 再将Q,F合成R，
mO(F)FdFsiln
mo(Q)Ql
②应用合力矩定理
mO(F)FxlFylctg
mo(Q)Ql
三、力偶的概念和性质
1、力偶的概念
力偶：两力大小相等，作用线不重合的反向平行力叫力偶。 性质1：力偶既没有合力，本身又不平衡，是一个基本力学量。
①两个同向平行力的合力
大小：R=Q+P
方向：平行于Q、P且指向一致
[例] 已知如图P、Q， 求平衡时 =？ 地面的反力ND=？
解：研究球受力如图， 选投影轴列方程为
X0 T2cosT10 ①
Y0T 2sin Q N D 0
②
由①得 cosT T122PP12 600
由②得N D Q -T 2 si n Q -2 P s6 i0 n 0 Q 3 P
[例] 求当F力达到多大时，球离开地面？已知P、R、h 解：研究块,受力如图，
解：①研究AB杆 ②画出受力图
③列平衡方程
X0 RAco sSCD co 40s5 0
Y0 P R A si n S Cs D4 i0 n 5 0
④解平衡方程 由EB=BC=0.4m，
解得：
tgE AB B1 0..2 41 3
SCD si4n05cPo4s05tg 4.2k 4N ； RASCDccoo4ss503.16kN
①力偶可以在其作用面内任 不变，可以任意改变力偶中力
意移动，而不影响它对刚体 的大小和相应力偶臂的长短，
的作用效应。
而不改变它对刚体的作用效应。
2、力偶系的合成与平衡
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系 设有两个力偶
d
d
m 1F 1d1;
m2F2d2
又m1P1d
m2P2d
RAP1P2' RBP1' P2
i1
[证] 由合力投影定理有： od=ob+oc
又∵ M o(F1)2oAoBA ob
M o(F 2)2oAoC A oc
M o(R)2oAoD A od
现 m o(R )m o(F 1)m o(F 2)证
[例] 已知：如图 F、Q、l, 求：mO (F ) 和 mo (Q )
解：①用力对点的矩法
Q',F'合成R'， 得到新力偶(R,R'), 将R,R'移到A',B'点，则(R,R')，取 代了原力偶(F，F' ) 并与原力偶等效。
比较(F,F')和(R,R')可得
m(F,F')=2△ABD=m(R,R') =2 △ABC
即△ABD= △ABC， 且它们转向相同。
由上述证明可得下列两个推论： ②只要保持力偶矩大小和转向
力偶无合力 R=F'-F=0
CB F' 1 C BCA
CA F
若 C C B d 成 B,必 立 C 有 B
d合力的作用点在 处无
mO(R)0
d
mO(F)mO(F')0 证明 mO(R)0为有限量 m O (F ) m O (F ') F (x d ) F 'x
FdmO(R)
由于O点是任取的
3）、不要画错力的方向 约束反力的方向必须严格地按照约束的类型来画，不 能单凭直观或根据主动力的方向来简单推想。在分析 两物体之间的作用力与反作用力时，要注意，作用力 的方向一旦确定，反作用力的方向一定要与之相反， 不要把箭头方向画错。
4)、受力图上不能再带约束。
即受力图一定要画在分离体上。
5)、受力图上只画外力，不画内力。 一个力，属于外力还是内力，因研究对象的不同，有 可能不同。当物体系统拆开来分析时，原系统的部分 内力，就成为新研究对象的外力。
③ MO (F )是影响转动的独立因素。 当F=0或d=0时，MO (F ) =0。
④单位N•m，工程单位kgf•m。 ⑤ MO (F ) =2⊿AOB=F•d ,2倍⊿形面积。
2、合力矩定理
定理：平面汇交力系的合力对平面内任一点的矩，等于所
有各分力对同一点的矩的代数和
即：
n
mO(R)mO(Fi)
6 )、同一系统各研究对象的受力图必须整体与局部一致， 相互协调，不能相互矛盾。
对于某一处的约束反力的方向一旦设定，在整体、局 部或单个物体的受力图上要与之保持一致。
7 )、正确判断二力构件。
2、受力图例题 画物体受力图主要步骤为：①选研究对象；②取分离体；
③画上主动力；④画出约束反力。 [例1]
当FP
h(2Rh)时球方能离开地面 Rh
解题技巧及说明： 1、一般地，对于只受三个力作用的物体，且角度
特殊时用 几 何法（解力三角形）比较简便。
2、一般对于受多个力作用的物体，且角度不特殊或 特殊，都用解析法。
3、投影轴常选择与未知力垂直，最好使每个方程中 只有一个未知数。
4、对力的方向判定不准的，一般用解析法。 5、解析法解题时，力的方向可以任意设，如果求出
负值，说明力方向与假设相反。对于二力构件， 一般先设为拉力，如果求出负值，说明物体受压 力。
§2–2 力的投影、力矩和力偶
力对物体可以产生 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向
二、力矩
1、力矩的概念
MO(F)Fd
+-
说明：① MO (F )是代数量。
② F↑,d↑转动效应明显。
解： ①选碾子为研究对象
②取分离体画受力图
∵当碾子刚离地面时NA=0,拉力F最大,这时 拉力F和自重及支反力NB构成一平衡力系。 由平衡的几何条件，力多边形封闭，故
FPtg
NBcoPs
又由几何关系：
tg
r2(rh)2 rh 0.577
所以
F=11.5kN , NB=23.1kN
由作用力和反作用力的关系，碾子对障碍物的压力等于23.1kN。