平面汇交力系的平衡条件及例题

平面力系-平面汇交力系的简化与平衡方程（常用版）(可以直接使用，可编辑完整版资料，欢迎下载）第2章平面力系192.1 平面汇交力系的简化与平衡方程 (19)2.2 力对点之矩合力矩定理 (24)2.3 力偶及其性质 (27)2.4 平面力偶系的合成与平衡方程 (30)2.5 平面一般力系的简化与平衡方程 (32)2.6 物体系统的平衡 (40)*附录Ⅱ：机械应用实例 (49)第2章平面力系本章主要介绍平面力系的简化与平衡问题，平面状态下物系平衡问题的解法。

按照力系中各力的作用线是否在同一平面内，可将力系分为平面力系和空间力系。

若各力作用线都在同一平面内并汇交于一点，则此力系称为平面汇交力系。

按照由特殊到一般的认识规律，我们先研究平面汇交力系的简化与平衡规律。

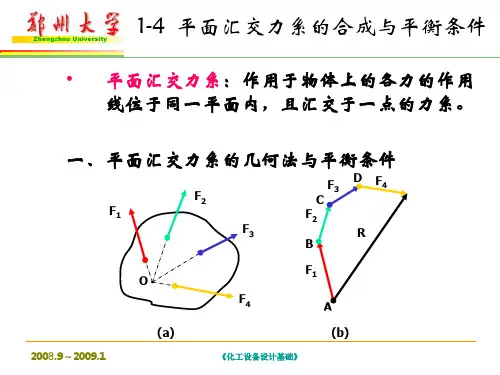
2.1 平面汇交力系的简化与平衡方程2.1.1 概述设刚体上作用有一个平面汇交力系F1、F2、…、F n，各力汇交于A点（图2-1a）。

根据力的可传性，可将这些力沿其作用线移到A点，从而得到一个平面共点力系（图2-1b）。

故平面汇交力系可简化为平面共点力系。

a ）b ）图2-1连续应用力的平行四边形法则，可将平面共点力系合成为一个力。

在图2-1b 中，先合成力F 1与F 2（图中未画出力平行四边形），可得力F R1，即 F R1＝F 1+ F 2；再将F R1与F 3合成为力F R2，即F R2＝F R1+ F 3；依此类推，最后可得F R ＝F 1+ F 2+…+ F n ＝∑F i （2-1）式中 F R 即是该力系的合力。

故平面汇交力系的合成结果是一个合力，合力的作用线通过汇交点，其大小和方向由力系中各力的矢量和确定。

因合力与力系等效，故平面汇交力系的平衡条件是该力系的合力为零。

2.1.2力在坐标轴上的投影过F 两端向坐标轴引垂线（图2-2）得垂足a 、b 、a'、b'。

线段ab 和a'b'分别为F 在x 轴和y轴上投影的大小，投影的正负号规定为：从a 到b （或从a'到b'）的指向与坐标轴正向相同为正，相反为负。

第二章-1 平面汇交力系与平面力偶系一、判别题（正确和是用√，错误和否×，填入括号内。

）2-1 平面汇交力系平衡的充分与必要的几何条件是：力多边形自行封闭。

（√）2-2 力在某一固定面上的投影是一个代数量。

（×）2-3 两个力F1、F2大小相等，则它们在同一轴上的投影也相等。

（×）2-4 一个力不可能分解为一个力偶；一个力偶也不可能合成一个力。

（√）2-5 力偶无合力、不能用一个力来等袒代替，也不能用一个力来平衡；（√）2-6 力偶无合力，也就是说力偶的合力等于零。

（×）2-7 力偶矩和力对点之矩本质上是二样的，讲的是一回事。

（×）2-8 力偶的作用效果取决于力偶矩的大小和转向。

（√）2-9 只要两力偶的力偶矩代数值相等，就是等效力偶。

（√）2-10 力偶中的两个力对同平面内任一点之矩的代数和等于力偶矩。

（√）2-11 力偶只能用力偶来平衡。

（√）2-12 平面力偶系可简化为一个合力偶。

（√）2-13 力偶可任意改变力的大小和力偶臂的长短。

（×）2-14 力偶的两力在其作用面内任意轴上的投影的代数和都等于零。

（√）2-15 若两个力F1、F2在同一轴上的投影相等，则这两个力相等，即F1 = F2。

（×）2-16 若两个力F1、F2大小相等，则在同一轴Ox上投影相等，即F1x = F2x。

（×）2-17 若两个力F1、F2大小、方向、作用点完全相同，则这两个力在任一轴上的投影相等。

（√）2-18 若两个力大小相等、方向相反，则在任一轴Ox上的投影大小相等。

（√）2-19 若两个力平行，则它们在任一轴上的投影相等。

（×）2-20 若两个力在某轴上的投影均为零，则该两力平行。

（√）2-21 图示为分别作用在刚体上A、B、C、D点的4个共面力，它们所构成的力多边形自行封闭且为平行四边形。

由于力多边形自行封闭，所以是平衡的。

教师课时教案课题： 2.2平面汇交力系的平衡目的与要求： 1、能说出平面力系的分类；2、知道平面汇交力系的平衡条件及其平衡方程；3、能运用平面汇交力系的平衡方程计算简单的平衡问题；4、感悟平面汇交力系的平衡问题在工程中的应用；5、通过对平衡问题计算步骤的理解，培养学生的力学素养。

教学模式及教学方法：教学模式：能设计实验，体验三个汇交力作用下处于平衡状态时物体的受力的大小变化以及受力的性质；能探究三个汇交力作用下平衡问题的解题方法。

教学方法：实验法、讲授法、类比法复习要点：力投影正负的判断和投影计算公式新课重点、难点：重点：运用平面汇交力系的平衡方程求解简单的平衡问题；难点：1、建立平面汇交力系的平衡方程；2、感悟平面汇交力系的平衡问题在工程中的应用。

解决措施：通过重点讲解、分步探讨让学生掌握如何解决汇交力系平衡问题本课小结：本节课我们主要学习了汇交力系的平衡方程及应用平衡方程解决力学中的平衡问题。

课外作业（或复习题）：1、通过本内容的学习，你有哪些收获？还存在哪些困惑？2、参观构件吊装的施工现场，运用所学知识对吊装方法加以说明。

课后改进措施: 重视基础知识的讲解，循序渐进，让学生打好基础，同时重视习题讲解，而且要让学生自己多练习。

教学过程一、引入1、如图一所示，手提一根弹簧，在弹簧下挂着一个重G=2N的砝码，问弹簧受到拉力有多大？2、在图一中，再用手把另一根弹簧沿水平方向十分缓慢地向右拉，如图二所示，问两根弹簧受到的拉力大小如何变化？如何计算呢？图一图二二、导学提纲1、平面力系的分类（1）各力的作用线全部的平面力系，称为平面平行力系。

（2）各力的作用线都的平面力系，称为平面汇交力系。

（3）各力的作用线即不全，也不全的平面力系，称为平面一般力系。

（4）平面力系按各力的划分为上述三类，请举例说明。

2、平面汇交力系的平衡条件及平衡方程。

（1）平面汇交力系的平衡条件是该力系的。

（2）平面汇交力系的平衡方程是，即力系中所有各力在两个坐标轴上的的代数和分别为。

第二章 平面汇交力系一、内容提要本章讲述了研究平面汇交力系的合成和平衡条件的两种方法：几何法和解析法。

1.求平面汇交力系的合力 (1) 几何法求合力。

根据力多边形法则求合力，即力多边形缺口的封闭边代表合力的大小和方向。

F R =ΣF合力的作用线通过原力系各力的汇交点。

(2) 解析法求合力。

根据合力投影定理，利用力系中各分力在两个正交轴上的投影的代数和，来确定合力的大小和方向为()()2Y 2X 2RY 2X R F F F F F R ∑+∑=+=XY XRY tan F F F F R ∑∑==αα为合力F R 与x 轴所夹的锐角。

合力F R 的指向由ΣF Y 和ΣF X 的正负号来确定，合力的作用线通过原力系各力的汇交点。

2.平面汇交力系的平衡条件(1) 平衡的必要和充分条件：平面汇交力系的合力为零，即F R =ΣF =0(2) 平衡的几何条件：平面汇交力系的力多边形自行封闭。

(3) 平衡的解析条件：平面汇交力系中所有各力在两个坐标轴上投影的代数和分别等于零。

即ΣF X =0 ΣF Y =0通过这两个独立的平衡方程，可求解出两个未知量。

3.力在坐标轴上的投影为F X =±F cosαF Y =±F sinα式中α为力F 与坐标轴x 所夹的锐角。

二、典型例题解析例 简易起重机如图2-1a 所示。

B 、C 为铰支座，钢丝绳的一端缠绕在卷扬机的点D 上。

杆件AB 、AC 及滑轮的自重不计，滑轮的半径也不计。

试求杆件AB 、AC 所受的力。

（空13行） 图2-1知识点：平面汇交力系的平衡条件及应用。

解 （1）取铰A 为研究对象。

杆AB 、AC 均为二力杆，可设为拉力。

由于A 处为定滑轮，故钢丝绳两端的拉力相等，都等于物体的重量W = 20kN 。

不计滑轮半径，则铰A 的受力图如图2-1b 所示。

（2）几何法求解作闭合的力多边形。

在选定比例尺后，先画已知力F T D 和W ，考虑到实际情况，F N C 应该为压力，所以应向上，且与水平成60°角。

作业A一、填空题1. 平面汇交力系是指力作用线＿＿＿＿＿＿＿＿＿＿，且＿＿＿＿＿＿＿＿＿一点的力系。

2. 平面汇交力系平衡的必要和充分条件是＿＿＿＿＿＿＿，此时力多边形＿＿＿＿＿＿＿。

3. 沿力矢量的两端向坐标轴作＿＿＿＿，两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影，力的投影是＿＿＿＿量，有正负之分。

4. 力沿直角坐标轴方向分解，通常，过力 F 矢量的两端向坐标轴作平行线构成矩形，力 F 是矩形的＿＿＿，矩形的＿＿＿＿是力F矢量的两个正交分力F x、F y 。

5. 已知一个力F沿直角坐标轴的两个投影为F x、F y ，那么这个力的大小F ＿＿＿＿，方向角＿＿＿＿。

( 角为F 力作用线与 x 轴所夹的锐角。

)6. 平面汇交力系的力多边形如图(a)，(b) ，(c)则图(a)中四个力关系的矢量表达式＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿；图(b) 中四个力关系的矢量表达式＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿；图(c)中四个力关系的矢量表达式＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿7. 如图所示，不计重量的直杆 AB 与折杆 CD 在 B 处用光滑铰链连接，若结构受力 F作用，9.平面刚架在 B 处受一水平力 F 作用，如图所示，刚架自重不计，设F =20 kN ，L =8 m ，h =4 m ，则求 A 、 D 处的约束反力，可以按以下步骤进行：1 ）以刚架为研究对象，进行受力分析：请画出刚架的受力分析图2 ）作用在刚架上的力（主动力和约束力）构成的力系属＿＿＿＿＿力系3 ）列出刚架的平衡方程（坐标如图）Fx 0 ：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿；则支座 C 处的约束力大小 ，方向8.如图所示，力 F在x 、y 轴上投影 F x ＝Fy＝7 题图）F y 0 ：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

（ 4 ）解方程计算A、D 处的约束反力F A = ＿＿＿＿＿＿；F D = ＿＿＿＿＿＿＿。

单元02 平面力系平面汇交力系的合成与平衡一、平面汇交力系合成的几何法1.两个共点力合成的几何法可以由力的平行四边形法则作，也可用力的三角形来作。

由余弦定理求合力的大小；由正弦定理确定合力方向2.任意个共点力合成的几何法结论：平面汇交力系的合力等于各分力的矢量和，合力的作用线通过各力的汇交点。

二、平面汇交力系平衡的几何条件平面汇交力系平衡的充要条件是：力系的合力等于零。

特点：最后一个力矢的终点与第一个力矢的起点相重合，即封闭边为零。

合力为零意味着力多边形自行封闭。

例：解：三、力在坐标轴上的投影四、合力投影定理1）平面汇交力系的合力F R= F1+ F2+…+ F n = ∑F2）合力在坐标轴的投影等于各分力在同轴上投影的代数和合力投影定理:力系的合力在某轴上的投影,等于力系中各力在同一轴上投影的代数和。

五、平面汇交力系的平衡方程平面汇交力系的平衡条件平衡方程:例题1：求如图所示平面共点力系的合力。

其中：F1 = 200 N，F2 = 300 N，F3 = 100 N，F4 = 250 N。

解：根据合力投影定理，得合力在轴 x，y上的投影分别为：合力的大小：171.3N合力与轴x的夹角的正切为：8.343所以，合力与轴x的夹角为41°例题2：如图所示是汽车制动机构的一部分。

司机踩到制动蹬上的力F=212 N，方向与水平面成 = 45°角。

当平衡时，DA铅直，BC水平，试求拉杆BC所受的力。

已知EA=24cm，DE=6 cm(点E在铅直线DA上) ，又B ，C ，D都是光滑铰链，机构的自重不计。

例题3：利用铰车绕过定滑轮B的绳子吊起一货物重G = 20 kN，滑轮由两端铰接的水平刚杆AB和斜刚杆BC支持于点B 。

不计铰车的自重，试求杆AB和BC 所受的力。

解析法的符号法则：当由平衡方程求得某一未知力的值为负时，表示原先假定的该力指向和实际指向相反。

解题技巧及说明：1、一般地，对于只受三个力作用的物体，且角度特殊时用几何法（解力三角形）比较简便。

作业A一、填空题1。

平面汇交力系是指力作用线＿＿＿＿＿＿＿＿＿＿，且＿＿＿＿＿＿＿＿＿一点的力系。

2。

平面汇交力系平衡的必要和充分条件是＿＿＿＿＿＿＿，此时力多边形＿＿＿＿＿＿＿。

3.沿力矢量的两端向坐标轴作＿＿＿＿，两垂足在坐标轴上截下的这段长度称为力在坐标轴上的投影，力的投影是＿＿＿＿量，有正负之分。

4.力沿直角坐标轴方向分解，通常，过力F 矢量的两端向坐标轴作平行线构成矩形，力F 是矩形的＿＿＿，矩形的＿＿＿＿是力F 矢量的两个正交分力y x F F 、。

5。

已知一个力F 沿直角坐标轴的两个投影为y x F F 、,那么这个力的大小=F ＿＿＿＿，方向角=α＿＿＿＿。

(角α为F 力作用线与x 轴所夹的锐角。

） 6。

平面汇交力系的力多边形如图（a)，（b ）,（c ）则图（a ）中四个力关系的矢量表达式＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿； 图(b ）中四个力关系的矢量表达式＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿； 图(c)中四个力关系的矢量表达式＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿。

7。

如图所示，不计重量的直杆AB 与折杆CD 在B 处用光滑铰链连接，若结构受力F 作用,则支座C 处的约束力大小＿＿＿＿＿＿，方向＿＿＿＿＿＿。

（7题图) (8题图）8.如图所示，力F 在y x 、轴上投影x F ＝＿＿＿＿＿、y F ＝＿＿＿＿＿.9.平面刚架在B 处受一水平力F 作用，如图所示,刚架自重不计，设F =20kN ，L =8m ，h =4m ，则求A 、D 处的约束反力，可以按以下步骤进行：(1）以刚架为研究对象，进行受力分析：请画出刚架的受力分析图(2）作用在刚架上的力（主动力和约束力）构成的力系属＿＿＿＿＿力系 （3）列出刚架的平衡方程（坐标如图）∑=0xF ：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿; ∑=0yF：＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿.（4）解方程计算D A 、处的约束反力A F =＿＿＿＿＿＿；D F =＿＿＿＿＿＿＿。