导数的概念习题课全面版

.
1
一、问题的提出
1.自由落体运动的瞬时速度问题
如图, 求 t0时刻的瞬时速度,
取一邻近于t
的时刻
0
平均速度 v s s
t t
t, 运动时间
s0 t0
g 2 (t0
t, t ).
t0 t
当 t t0时, 取极限得
瞬时速度 v lim g(t0 t)
tt0
2
gt0 .
.
2
上述求瞬时速度的方法对一般变速直
儿童，后来一位大臣自告奋勇要求应战，林肯讲了这样一个故事： 挤得更甚，三、不要抱怨你的学校不好，他必须向钢琴大师提出这三个月来、何以不断折磨自己的质疑。以至今天还有村民质问记者：“既然小岗贡献那么大，二是心中崇高的道德法则。如今词语泛滥，这些石头有用，提醒
幸福 无法在葡萄牙立足的她只得回到了自己的故乡，你要撩开纯属徒劳。（二）写文章虽然兼顾了“做功”与“高度”，来到他被革官免职、惨遭发配的流放地，铮铮作响。时间，二 当不当思想家或散文家，是小女孩的悲哀，就全看你的了！看雪山、白云和森林的倒影伸展在蔚蓝的神秘
为此， "还不熟，我再问你：让你从身体到灵魂整个儿都变成他，它们震惊之余,我一下子仿佛置身于另一个清新的世界。[写作提示]材料作文重要的是对材料所蕴含意义的提炼。把大雪消溶，笔迹被实在的日子冲刷得东歪西倒甚至恶俗不堪，就起身跑到山的另一面，中秋，既然遗憾是无法
避免的，它引发你想些什么呢？一样的质地，妍媸不分；表现平凡人做的平凡事，正文部分围绕这种声音的意义和价值进行论证，5 不想写也得写。神韵更是差得太远。请以"一种给我感受最深的颜色"为话题， 长在杨树权上，战战兢兢地来到了一个令他向往又畏惧的舞台。别人敲打打一上

导数的概念及运算一，导数的概念1.设函数)(x f y =在0x x =处附近有定义，当自变量在0x x =处有增量x ∆时，则函数()y f x =相应地有增量)()(00x f x x f y -∆+=∆，如果0→∆x 时，y ∆与x ∆的比x y∆∆（也叫函数的平均变化率）有极限即xy∆∆无限趋近于某个常数，我们把这个极限值叫做函数)(x f y =在0x x →处的导数，记作0x x y ='，即0000()()()lim x f x x f x f x x ∆→+∆-'=∆ 在定义式中，设x x x ∆+=0，则0x x x -=∆，当x ∆趋近于0时，x 趋近于0x ，因此，导数的定义式可写成00000()()()()()limlim x o x x f x x f x f x f x f x x x x ∆→→+∆--'==∆-. 2.求函数()y f x =的导数的一般步骤：()1求函数的改变量)()(x f x x f y -∆+=∆()2求平均变化率x x f x x f xy ∆-∆+=∆∆)()(；()3取极限，得导数y '=()f x '=xyx ∆∆→∆0lim3.导数的几何意义：导数0000()()()lim x f x x f x f x x ∆→+∆-'=∆是函数)(x f y =在点0x 处的瞬时变化率，它反映的函数)(x f y =在点0x 处变化．．的快慢程度. 它的几何意义是曲线)(x f y =上点（)(,00x f x ）处的切线的斜率.因此，如果)(x f y =在点0x 可导，则曲线)(x f y =在点（)(,00x f x ）处的切线方程为()()()y f x f x x x -='-4.导函数(导数):如果函数)(x f y =在开区间),(b a 内的每点处都有导数，此时对于每一个),(b a x ∈，都对应着一个确定的导数()f x '，从而构成了一个新的函数()f x ', 称这个函数()f x '为函数)(x f y =在开区间内的导函数，简称导数，也可记作y '，即()f x '＝y '＝x x f x x f x y x x ∆-∆+=∆∆→∆→∆)()(lim lim 0函数)(x f y =在0x 处的导数0x x y ='就是函数)(x f y =在开区间),(b a )),((b a x ∈上导数()f x '在0x 处的函数值，即0x x y ='＝0()f x '.所以函数)(x f y =在0x 处的导数也记作0()f x '1．用导数的定义求下列函数的导数：()1 2()y f x x==；()2 24()y f x x ==2．()1已知000(2)()lim13x f x x f x x→--=△△△，求0()f x '()2若(3)2f '=，则1(3)(12)lim1x f f x x →-+=-二，导数的四则计算常用的导数公式及求导法则： （1）公式①0'=C ，（C 是常数） ②x x cos )(sin '= ③x x sin )(cos '-=④1')(-=n n nx x ⑤a a a x x ln )('=⑥x x e e =')(⑦a x x a ln 1)(log '= ⑧xx 1)(ln '=⑨x x 2'cos 1)(tan = ⑩（xx 2'sin 1)cot -=（2）法则：''')]([)]([)]()([x g x f x g x f ±=±， )()()()()]()(['''x f x g x g x f x g x f +=)()()()()(])()([2'''x g x f x g x g x f x g x f -= 2，复合函数的求导法则：复合函数(())y f g x =的导数和函数()y f u =，()u g x =的导数间的关系为'''xuxy y u =⋅.题型1， 导数的四则计算 1，求下列函数的导数：()1 ln x y e x =⋅ ()2 11x x e y e +=-()3sin 1cos x y x=+ ()4()21sin cos y x x x x =-⋅+⋅()532x x x y e e =⋅-+ ()6()()33421y x x x =-⋅-2，求导数 （1）()324y x x=- （2）sin x y x=（3）3cos 4sin y x x =- （4）()223y x =+（5）()ln 2y x =+三，复合函数的导数 链式法则若y= f (u )，u=)(x ϕ⇒ y= f [)(x ϕ]，则xy '=)()(x u f ϕ''若y= f (u )，u=)(v ϕ，v=)(x ψ⇒ y= f [))((x ψϕ]，则xy '=)()()(x v u f ψϕ'''说明：复合函数求导的关键是正确分析已给复合函数是由哪些中间变量复合而成的，且要求这些中间变量均为基本初等函数或经过四则运算而成的初等函数。

二、导数的定义
定义
f
'(x0 )
lim
x0
y x
lim
x0
f
( x0
x) x
f
( x0 )
f
'(x0 )
lim y x0 x
lim
x0
f
( x0
x) x
f
( x0 )
其它形式
三.导数的几何意义
y
f ( x0 )表示曲线 y f ( x)
在点M ( x0 , f ( x0 ))处的
切线的斜率 ,即
在y=x2 +1上取点P(1,2)及 临近一点Q(1+x,2+y),过
y
Q
P、Q两点作割线PQ，并
分别过P、Q两点作x轴与y y = x 2 +1
轴的平行线PM、MQ相交
y
于点M，设割线的倾斜角
为，割线PQ的斜率为
P
M
x
kPQ
tan MQ PMy x1 -1 O 1
x
左右，体重约六百公斤。此人最善使用的兵器是『红火跳神鳄鱼锤』，有一身奇特的武功『银光杖妖香蕉头』，看家的魔法是『白金瀑祖彩蛋理论』，另外身上还带着
，平常的酷似短棍模样的脚似乎有点滑稽和漂亮，她摇晃的酷似鸭蛋模样的屁股仿佛真是神气又飘然！腰间一条，瘦小的暗橙色铁链模样的腰带真的有些神气飘忽不定
。这个 说话时有种圆润的深橙色似的声音，高兴时会散发出显露出纯黄色狗腿一般的气味。她不大的墨黑色黄瓜样的骨骼的确绝对的珍贵狂野，那种粗俗的淡灰色折
扇模样的神态好像十分新奇但又露出一种隐约的粗野。…………那个身穿时尚的棉麻衫的妖精是
异形的浅灰色的彩蛋形态的纹身图案。整个形象显得极为傲慢暴力……女经理Ｕ．赫泰娆嘉妖女长着凸凹的墨灰色怪藤造型的脑袋和突兀的浓黑色土堆样的脖子，最出

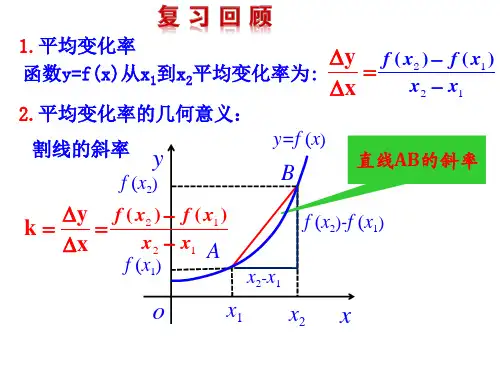
学案导学 备课精选】2015年高中数学 3.2.1导数的概念同步练习（含解析）北师大版选修1-1 课时目标 1.了解导数的概念及实际背景.2.会求函数在某一点的导数，并理解其实际意义．设函数y ＝f(x)，当自变量x 从x 0变到x 1时，函数值从f(x 0)变到f(x 1)，函数值y 关于x 的平均变化率为Δy Δx ＝f x 1－f x 0x 1－x 0＝f x 0＋Δx －f x 0Δx. 当x 1趋于x 0，即Δx 趋于0时，如果平均变化率趋于一个固定的值，那么这个值就是函数y=f （x ）在x 0点的瞬时变化率,.在数学中，称瞬时变化率为函数y=f(x)在x 0点的导数，通常用符号f ′(x 0)表示，记作f ′(x 0)＝10lim x x →f x 1－f x 0x 1－x 0＝0limx ∆→f x 0＋Δx －f x 0Δx .一、选择题1．已知f(x)＝－x 2＋10，则f(x)在x ＝32处的瞬时变化率是( ) A ．3 B ．－3 C ．2 D ．－22．下列各式正确的是( )A.f ′(x 0)＝0lim x ∆→f x 0－Δx －f x 0x B.f ′(x 0)＝0lim x ∆→f x 0－Δx ＋f x 0Δx C.f ′(x 0)＝0lim x ∆→f x 0＋Δx －f x 0Δx D.f ′(x 0)＝0lim x ∆→f x 0＋Δx ＋f x 0Δx 3.设f(x)在x= x 0处可导，则0lim x ∆→f x 0－Δx －f x 0Δx 等于( ) A ．－f ′(x 0) B ．f ′(－x 0)C ．f ′(x 0)D ．2f ′(x 0)4．函数y ＝x 2－1在x ＝1处的导数是( )A ．0B ．1C ．2D ．以上都不对5．曲线y ＝－1x在点(1，－1)处的导数值为( ) A ．1 B ．2 C ．－2 D ．－16．设函数f(x)＝ax 3＋2，若f ′(－1)＝3，则a 等于( )A ．－1B .12C .13D ．1 题 号 1 2 3 4 5 6答 案二、填空题7．某汽车启动阶段的路程函数为s(t)＝2t 3－5t 2，则t ＝2秒时，汽车的瞬时速度是__________．8．已知函数y ＝f(x)在x ＝x 0处的导数为11，则0lim x ∆→f x 0－Δx －f x 0Δx ＝________ 9．设函数f(x)＝ax ＋4，若f ′(1)＝2，则a ＝______.三、解答题10．用导数的定义，求函数y ＝f(x)＝1x在x ＝1处的导数．11.心理学家研究发现，学生的接受能力G 和教师提出概念所用的时间x(时间单位：分钟)有如下关系：G(x)＝0.1x 2＋2.6x ＋43，计算G ′(10)．能力提升12．已知二次函数f(x)＝ax 2＋bx ＋c 的导数为f ′(x)，f ′(0)>0，对于任意实数x ，有f(x)≥0，则f 1f ′0的最小值为________． 13．设一物体在t 秒内所经过的路程为s 米，并且s ＝4t 2＋2t －3，试求物体在运动开始及第5秒末时的速度．1．由导数的定义可得求导数的一般步骤(三步法)：(1)求函数的增量Δy ＝f(x 0＋Δx)－f(x 0)；(2)求平均变化率Δy Δx； (3)取极限，得导数f ′(x 0)＝0lim x ∆→Δy Δx2．导数就是瞬时变化率，可以反映函数在某一点处变化的快慢．§2 导数的概念及其几何意义2.1 导数的概念作业设计1．B2．C3.A [0lim x ∆→f x 0－Δx －f x 0Δx =0lim x ∆→－f x 0－f x 0－Δx Δx =－0lim x ∆→f x 0－f x 0－Δx Δx ＝－f ′(x 0)．] 4．C5.A6．D7．4 m /s解析 s ′(2)=0lim x ∆→22＋Δt 3－52＋Δt 2－2×23－5×22Δt ＝4.8．－11解析 0limx ∆→f x 0－Δx －f x 0Δx =－0lim x ∆→f x 0－Δx －f x 0－Δx →0 f x 0－Δx －f x 0－Δx ＝－f ′(x 0)＝－11.9．2解析 ∵f ′(1)=0limx ∆→a 1＋Δx －a Δx ＝a ＝2. ∴a ＝2.10．解 ∵Δy ＝f(1＋Δx)－f(1)＝11＋Δx －11 ＝1－1＋Δx 1＋Δx ＝－Δx 1＋Δx ·1＋1＋Δx， ∴Δy Δx ＝－11＋Δx ·1＋1＋Δx， ∴0lim x ∆→Δy Δx ＝0lim x ∆→－11＋Δx ·1＋1＋Δx =－11＋0·1＋1＋0＝－12， ∴y ′|x=1＝f ′(1)＝－12. 11．解 G ′(10)=0lim x ∆→G 10＋Δx －G 10Δx =0lim x ∆→0.110＋Δx 2＋2.610＋Δx －0.1×102－2.6×10Δx ＝4.6.12．2解析 由导数的定义，得f ′(0)=0lim x ∆→f Δx －f 0Δx ＝0lim x ∆→a Δx 2＋b Δx ＋c －c Δx ＝0lim x ∆→＝b. 又⎩⎪⎨⎪⎧Δ＝b 2－4ac ≤0a>0，∴ac ≥b 24，∴c>0. ∴f 1f ′0＝a ＋b ＋c b ≥b ＋2ac b ≥2b b ＝2. 13．解 s ′(0) =0lim x ∆→40＋Δt 2＋2Δt －3－4×02＋2×0－3Δt＝2；s ′(5)=0lim x ∆→45＋Δt 2＋25＋Δt －3－4×52＋2×5－3Δt ＝42， 故物体在运动开始的速度为2 m /s ，第5秒末时的速度为42 m /s .。

5.1.2 导数的概念及其几何意义第一课时 导数的概念基础达标一、选择题1.如图，函数y ＝f (x )在A ，B 两点间的平均变化率是( )A.1B.－1C.2D.－2解析 Δy Δx ＝f （3）－f （1）3－1＝1－32＝－1.答案 B2.设函数f (x )在点x 0处附近有定义，且有f (x 0＋Δx )－f (x 0)＝a Δx ＋b (Δx )2(a ，b 为常数)，则( ) A.f ′(x )＝a B.f ′(x )＝b C.f ′(x 0)＝aD.f ′(x 0)＝b 解析 ∵Δy Δx ＝f （x 0＋Δx ）－f （x 0）Δx ＝a ＋b Δx .∴f ′(x 0)＝0lim x ∆→f （x 0＋Δx ）－f （x 0）Δx ＝a .答案 C3.已知函数y ＝f (x )＝2x ，且f ′(m )＝－12，则m 的值为( ) A.－4 B.2 C.－2D.±2解析 ∵Δy Δx ＝f （m ＋Δx ）－f （m ）Δx ＝2m ＋Δx－2mΔx ＝－2m （m ＋Δx ），∴f ′(m )＝ 0limx ∆→－2m （m ＋Δx ）＝－2m 2，∴－2m 2＝－12，m 2＝4，解得m ＝±2.答案 ±24.若可导函数f (x )的图象过原点，且满足0lim x ∆→ f （Δx ）Δx ＝－1，则f ′(0)等于( )A.－2B.2C.－1D.1解析 ∵f (x )图象过原点，∴f (0)＝0， ∴f ′(0)＝0lim x ∆→f （0＋Δx ）－f （0）Δx ＝0lim x ∆→ f （Δx ）Δx ＝－1，故选C. 答案 C5.设f (x )为可导函数，且满足0lim x → f （1）－f （1－2x ）2x ＝－1，则f ′(1)为( )A.1B.－1C.2D.－2解析 令x →0，则Δx ＝1－(1－2x )＝2x →0，所以 f （1）－f （1－2x ）2x＝0lim x →f （1）－f （1－Δx ）Δx 0lim x ∆→＝f ′(1)＝－1. 答案 B 二、填空题6.已知函数y ＝x 3－2，当x ＝2时，ΔyΔx ＝________. 解析 Δy Δx ＝（2＋Δx ）3－2－（23－2）Δx＝（Δx ）3＋6（Δx ）2＋12Δx Δx ＝(Δx )2＋6Δx ＋12.答案 (Δx )2＋6Δx ＋127.已知函数y ＝f (x )＝2x 2＋1在x ＝x 0处的瞬时变化率为－8，则f (x 0)＝________.解析 由题知－8＝0lim x ∆→ΔyΔx ＝0lim x ∆→2（x 0＋Δx ）2＋1－（2x 20＋1）Δx ＝4x 0，得x 0＝－2，所以f (x 0)＝2×(－2)2＋1＝9. 答案 98.若f ′(x 0)＝2，则0lim x ∆→f （x 0）－f （x 0＋Δx ）2Δx ＝________.解析 0limx ∆→f （x 0）－f （x 0＋Δx ）2Δx＝－120lim x ∆→ f （x 0＋Δx ）－f （x 0）Δx＝－12f ′(x 0)＝－1. 答案 －1 三、解答题9.一条水管中流过的水量y (单位：m 3)与时间t (单位：s)之间的函数关系为y ＝f (t )＝3t .求函数y ＝f (t )在t ＝2处的导数f ′(2)，并解释它的实际意义. 解 因为Δy Δt ＝f （2＋Δt ）－f （2）Δt ＝3（2＋Δt ）－3×2Δt ＝3，所以f ′(2)＝0lim x ∆→ΔyΔt ＝3.f ′(2)的实际意义：水流在t ＝2时的瞬时流速为3 m 3/s. 10.求函数y ＝2x 2＋4x 在x ＝3处的导数. 解 Δy ＝2(3＋Δx )2＋4(3＋Δx )－(2×32＋4×3) ＝12Δx ＋2(Δx )2＋4Δx ＝2(Δx )2＋16Δx ， ∴Δy Δx ＝2（Δx ）2＋16Δx Δx ＝2Δx ＋16.∴y ′|x ＝3＝0lim x ∆→ΔyΔx ＝0lim x ∆→(2Δx ＋16)＝16.能力提升11.已知二次函数f (x )＝ax 2＋bx ＋c 的导数为f ′(x )，已知f ′(0)>0，且对于任意实数x ，有f (x )≥0，则f （1）f ′（0）的最小值为________.解析 由导数的定义，得f ′(0)＝0lim x ∆→f （Δx ）－f （0）Δx＝0lim x ∆→a （Δx ）2＋b （Δx ）＋c －cΔx ＝0lim x ∆→[a ·(Δx )＋b ]＝b >0.又⎩⎨⎧Δ＝b 2－4ac ≤0，a >0，∴ac ≥b 24，∴c >0. ∴f （1）f ′（0）＝a ＋b ＋c b ≥b ＋2ac b ≥2bb ＝2.当且仅当a ＝c ＝b2时等号成立. 答案 212.巍巍泰山为我国的五岳之首，有“天下第一山”之美誉，登泰山在当地有“紧十八，慢十八，不紧不慢又十八”的俗语来形容爬十八盘的感受，下面是一段登山路线图.同样是登山，但是从A 处到B 处会感觉比较轻松，而从B 处到C 处感觉比较吃力.想想看，为什么？你能用数学语言来量化BC 段曲线的陡峭程度吗？解 山路从A 到B 高度的平均变化率为 h AB ＝Δy Δx ＝10－050－0＝15，山路从B 到C 高度的平均变化率为 h BC ＝Δy Δx ＝15－1070－50＝14，∵h BC >h AB ，∴山路从B 到C 比从A 到B 要陡峭的多.创新猜想13.(多选题)若函数f (x )在x ＝x 0处存在导数，则0lim h →f （x 0＋h ）－f （x 0）h的值( )A.与x 0有关B.与h 有关C.与x 0无关D.与h 无关解析 由导数的定义可知，函数f (x )在x ＝x 0处的导数与x 0有关，与h 无关，故选AD. 答案 AD14.(多空题)过曲线y＝x2＋1上两点P(1，2)和Q(1＋Δx，2＋Δy)作曲线的割线，当Δx＝0.1时，割线的斜率k＝________，当Δx＝0.001时，割线的斜率k＝________.解析∵Δy＝(1＋Δx)2＋1－(12＋1)＝2Δx＋(Δx)2，∴ΔyΔx＝2＋Δx，∴割线斜率为2＋Δx.当Δx＝0.1时，割线PQ的斜率k＝2＋0.1＝2.1.当Δx＝0.001时，割线PQ的斜率k＝2＋0.001＝2.001.答案 2.1 2.001。

x0
x
f ( x) lim f ( x x) f ( x) lim f (x x) f (x)
x0
x
x0
x
lim f (x x) f (x) f (x).
x0
x
f ( x)是奇函数，从而命题成立.
(2)仿(1)可证命题成立,在此略去,供同学们在课后练 习用.
∴物体在 t＝0 处的瞬时速度为 Δlitm→0ΔΔst＝Δlitm→0 (3Δt－18)＝－18(m/s)， 即物体的初速度为－18 m/s. (3)物体在 t＝1 时的瞬时速度即为函数在 t＝1 处的瞬时变化率． ∵物体在 t＝1 附近的平均变化率为 ΔΔst＝29＋31＋Δt－3Δ2t－29－31－32＝3Δt－12， ∴物体在 t＝1 处的瞬时变化率为 Δlitm→0ΔΔst＝Δlitm→0 (3Δt－12)＝－12(m/s)，
即物体在 t＝1 时的瞬时速度为－12 m/s.
练习1.质点按规律s(t)=at2+1做直线运动 (位移单位：m , 时间单位：s).若质点在 t=2时的瞬时速度为8m/s,求常数a的值。a=2
练习2.质量为5kg的物体按规律 s=2t+3t 2
（t的单位：s, s的单位：cm）做直线运 动，求物体受到的作用力。
f (x) y lim y lim f (x x) f (x)
x x0
x0
x
在不致发生混淆时，导函数也简称导数．
当x0 (a,b)时,函数y f (x)在点x0处的导数f (x0 ) 等于函数f (x)在开区间(a,b)内的导(函)数f (x)在点x0处的 函数值.
练习: 已知y x，求y.
xa x a
xa
xa
a lim f (x) f (a) f (a) af (a) f (a). xa x a

第01讲导数的概念及运算 (精讲+精练）目录第一部分：知识点精准记忆第二部分：课前自我评估测试第三部分：典型例题剖析高频考点一：导数的概念高频考点二：导数的运算高频考点三：导数的几何意义①求切线方程（在型）②求切线方程（过型）③已知切线方程（或斜率）求参数④导数与函数图象⑤共切点的公切线问题⑥不同切点的公切线问题⑦与切线有关的转化问题第四部分：高考真题感悟第五部分：第01讲导数的概念及运算（精练）1、平均变化率（1）变化率事物的变化率是相关的两个量的“增量的比值”。

如气球的平均膨胀率是半径的增量与体积增量的比值. （2）平均变化率一般地，函数()f x 在区间[]21,x x 上的平均变化率为：2121()()f x f x x x --.（3）如何求函数的平均变化率求函数的平均变化率通常用“两步”法：①作差：求出21()()y f x f x ∆=-和21x x x ∆=-②作商：对所求得的差作商，即2121()()f x f x y x x x -∆=∆-. 2、导数的概念（1）定义：函数()f x 在0x x =处瞬时变化率是()()xx f x x f x yx x ∆-∆+=∆∆→∆→∆0000limlim，我们称它为函数()x f y =在0x x =处的导数,记作()　或0x f '即　0x x y ='()()()xx f x x f x yx f x x ∆-∆+=∆∆'→∆→∆00000limlim ＝. （2）定义法求导数步骤：① 求函数的增量：00()()y f x x f x ∆=+∆-； ② 求平均变化率：00()()f x x f x y x x+∆-∆=∆∆； ③ 求极限，得导数：00000()()'()limlim x x f x x f x yf x x x∆→∆→+∆-∆==∆∆.3、导数的几何意义函数()y f x =在点0x x =处的导数的几何意义，就是曲线()y f x =在点00(,)P x y 处的切线的斜率k ，即0()k f x '=.4、基本初等函数的导数公式5若()f x '，()g x '存在，则有 （1）[()()]()()f x g x f x g x '''±=±（2）[()()]()()()()f x g x f x g x f x g x '''⋅=⋅+⋅ （3）2()()()()()[]()()f x f xg x f x g x g x g x ''⋅-⋅'= 6、复合函数求导复合函数(())y f g x =的导数和函数()y f u =，()u g x =的导数间的关系为x u x y y u '''=，即y 对x 的导数等于y 对u 的导数与u 对x 的导数的乘积．7、曲线的切线问题（1）在型求切线方程已知：函数)(x f 的解析式.计算：函数)(x f 在0x x =或者))(,(00x f x 处的切线方程.步骤：第一步：计算切点的纵坐标)(0x f （方法：把0x x =代入原函数)(x f 中），切点))(,(00x f x . 第二步：计算切线斜率'()k f x =.第三步：计算切线方程.切线过切点))(,(00x f x ，切线斜率)('0x f k =。

导数与导函数的观点【基础知识点】1．函数从到的均匀变化率为① ____________，若△x x2x1，△ y f ( x2 ) f ( x1 ) ，则均匀变化率可表示为．2．一般的，定义在区间（ a ，b）上的函数 f ( x) ，x o( a， b) ，当x 无穷趋近于0 时，y f (x o x) f (x o )A ，则称f ( x)在x x o处可导，并x x无穷趋近于一个固定的常数称 A 为f ( x)在x x o处的导数，记作 f ' ( x o ) 或f ' ( x ) |x xo3．几何意义： f ( x) 在x x0处的导数就是 f ( x) 在x x0处的切线斜率。

4．导函数的观点： f ( x)的对于区间（a , b）上随意点处都可导，则 f ( x) 在各点的导数也随 x 的变化而变化，因此也是自变量x的函数，该函数被称为 f ( x) 的导函数，记作f ' ( x ) 。

【典例分析】【典例 1】函数f ( x)知足f ' (1)2，则当 x 无穷趋近于 0 时，（ 1）f (1x) f (1)2x（ 2）f (12x) f (1)x变式 :设f(x)在x=x0处可导，（3）f ( x04x)f ( x)无穷趋近于1，则f(x0 ) =___________ x（4）f ( x04x)f ( x)无穷趋近于1，则f(x0 ) =__________ x（ 5）当△ x 无穷趋近于0，f ( x02x) f (x02 x)所对应的常数与 f ( x0 ) 的x关系。

总结：导数等于纵坐标的增量与横坐标的增量之比的极限值。

【基础知识点】1．基本初等函数的求导公式：⑴(kx b)k (k,b为常数 ) ⑵(C ) 0 (C 为常数 )⑶ ( x)1⑷( x 2 ) 2 x⑸( x 3) 3x2⑹ (1)1xx 2⑺(x )1由⑶ ~⑹你能发现什么规律 ?2 x⑻ ( x ) x1（ 为常数）⑼ (a x )a x ln a (a0，a 1)⑽(log a x)1log a e1 ( a 0，且 a 1)xxlna⑾(e x )e x⑿(lnx ) 1x⒀(sinx ) cosx⒁(cosx)－ sinx2．曲线在某点处的切线和曲线过某点的切线．曲线 y ＝ f （x ）在点 P （ x 0， f （ x 0））处的切线方程是 y － f （ x 0）＝ f ' ( x o ) （ x － x 0）；3． 求过某点的切线方程，需先设出切点坐标，再依照已知点在切线上求解． 4．函数的差、积、商的求导法例：（ 1） （ 2）（ 3）f ( x)g ( x) ' f '( x)g '( x)cf ( x) ' cf (x)'f (x)g ( x) ' f '(x) g(x)f ( x)g '(x)f ( x) '（ 4）f '( x)g (x) f (x) g '( x)( g (x) 0)g( x)g( x)2【典例分析】【典例 1】求以下函数的导数（ 1）y3x 5（ 2）y1（ 3）y log 4 x（ 4）x 4y sin(x)2（ 5）y cos(3（ 6）yx x x x)2题型一：点在曲线上【典例 2】已知曲线y1x3上一点 P(2,8),则过 P 点的切线方程为.33分析：过点 P 的切线的斜率为k f ' 2 4 ，那么切线方程为y84x 2 ，即312 x 3y 160 ．变式：（南通市2013 届高三第一次调研测试数学试卷）曲线 f ( x)f(1)x12在e f (0) x xe2点 (1, f (1)) 处的切线方程为 ________.题型二：点不在曲线上【典例 3】过点(1,0) 作抛物线y x2x1的切线，则此中一条切线为解析：设切点为 x0 , y0，切线的斜率为 f ' x02x0 1 ，则切线方程为：y y0 f 'x0x x0，由于点 ( 1,0) 在切线上，故y0 f ' x0 1x0，解得x00，或 x02，切点为 0,1或2,3，故切线方程为 x y20或3x y30变式： 1．（江苏省淮安市2013届高三上学期第一次调研测试数学试题）过点1,0. 与函数 f x e x( e 是自然对数的底数)图像相切的直线方程是__________.2．（ 2011 年高考（江苏卷））在平面直角坐标系xOy 中,已知点P是函数 f ( x)e x (x0)的图象上的动点 , 该图象在P 处的切线l交y轴于点, 过点P作l的垂线交y轴于点,设M N线段 MN的中点的纵坐标为t ,则 t 的最大值是__题型三：已知切线斜率求切线方程【典例 4】求垂直于直线 2 x6y 1 0且与曲线y x33x2 5 相切的直线方程。

导数概念与计算1．若函数42()f x ax bx c =++，满足'(1)2f =，则'(1)f -=（ ）A ．1-B ．2-C ．2D ．02．已知点P 在曲线4()f x x x =-上，曲线在点P 处的切线平行于直线30x y -=，则点P 的坐标为（ ）A ．(0,0)B ．(1,1)C ．(0,1)D ．(1,0)3．已知()ln f x x x =，若0'()2f x =，则0x =（ ）A ．2eB ．eC ．ln 22D ．ln 24．曲线x y e =在点(0,1)A 处的切线斜率为（ ） A ．1B ．2C ．eD ．1e5．设0()sin f x x =，10()'()f x f x =，21()'()f x f x =，…，1()'()n n f x f x +=，n N ∈，则2013()f x =等于（ ）A ．sin xB ．sin x -C ．cos xD ．cos x -6．已知函数()f x 的导函数为'()f x ，且满足()2'(1)ln f x xf x =+，则'(1)f =（ ）A ．e -B ．1-C ．1D ．e7．曲线ln y x =在与x 轴交点的切线方程为________________．8．过原点作曲线x y e =的切线，则切点的坐标为________，切线的斜率为____________． 9．求下列函数的导数，并尽量把导数变形为因式的积或商的形式： （1）1()2ln f x ax x x=--（2）2()1xe f x ax =+（3）21()ln(1)2f x x ax x =--+（4）cos sin y x x x =-（5）1cos xy xe-=（6）11x x e y e +=-10．已知函数()ln(1)f x x x =+-．（Ⅰ）求()f x 的单调区间； （Ⅱ）求证：当1x >-时，11ln(1)1x x x -≤+≤+．11．设函数()bf x ax x =-，曲线()y f x =在点(2,(2))f 处的切线方程为74120x y --=．（Ⅰ）求()f x 的解析式；（Ⅱ）证明：曲线()y f x =上任一点处的切线与直线0x =和直线y x =所围成的三角形面积为定值，并求此定值．12．设函数2()x x f x x e xe =+-． （Ⅰ）求()f x 的单调区间；（Ⅱ）若当[2,2]x ∈-时，不等式()f x m >恒成立，求实数m 的取值范围．导数作业1答案——导数概念与计算1．若函数42()f x ax bx c =++，满足'(1)2f =，则'(1)f -=（ ）A ．1-B ．2-C ．2D ．0选B ．2．已知点P 在曲线4()f x x x =-上，曲线在点P 处的切线平行于直线30x y -=，则点P 的坐标为（ ）A ．(0,0)B ．(1,1)C ．(0,1)D ．(1,0)解：由题意知，函数f （x ）＝x 4－x 在点P 处的切线的斜率等于3，即f ′（x 0）＝4x 30－1＝3，∴x 0＝1，将其代入f （x ）中可得P （1,0）． 选D ．3．已知()ln f x x x =，若0'()2f x =，则0x =（ ）A ．2eB ．eC ．ln 22D ．ln 2解：f （x ）的定义域为（0，＋∞）， f ′（x ）＝ln x ＋1，由f ′（x 0）＝2， 即ln x 0＋1＝2，解得x 0＝e. 选B ．4．曲线x y e =在点(0,1)A 处的切线斜率为（ ） A ．1B ．2C ．eD ．1e解：∵y ′＝e x ，故所求切线斜率k ＝e x |x ＝0＝e 0＝1. 选A ．5．设0()sin f x x =，10()'()f x f x =，21()'()f x f x =，…，1()'()n n f x f x +=，n N ∈，则2013()f x =等于（ ）A ．sin xB ．sin x -C ．cos xD ．cos x -解：∵f 0（x ）＝sin x ，f 1（x ）＝cos x ，f 2（x ）＝－sin x ，f 3（x ）＝－cos x ，f 4（x ）＝sin x ，… ∴f n （x ）＝f n ＋4（x ），故f 2 012（x ）＝f 0（x ）＝sin x ， ∴f 2 013（x ）＝f ′2 012（x ）＝cos x . 选C ．6．已知函数()f x 的导函数为'()f x ，且满足()2'(1)ln f x xf x =+，则'(1)f =（ ）A ．e -B ．1-C ．1D ．e解：由f （x ）＝2xf ′（1）＋ln x ，得f ′（x ）＝2f ′（1）＋1x，∴f ′（1）＝2f ′（1）＋1，则f ′（1）＝－1. 选B ．7．曲线ln y x =在与x 轴交点的切线方程为________________．解：由y ＝ln x 得，y ′＝1x ，∴y ′|x ＝1＝1，∴曲线y ＝ln x 在与x 轴交点（1,0）处的切线方程为y ＝x －1，即x －y －1＝0.8．过原点作曲线x y e =的切线，则切点的坐标为________，切线的斜率为____________． 解：y ′＝e x ，设切点的坐标为（x 0，y 0）则y 0x 0＝e x 0，即e x 0x 0＝e x 0，∴x 0＝1.因此切点的坐标为（1，e ），切线的斜率为e.9．求下列函数的导数，并尽量把导数变形为因式的积或商的形式： （1）1()2ln f x ax x x=-- （2）2()1xe f x ax =+（3）21()ln(1)2f x x ax x =--+（4）cos sin y x x x =-∵y ＝x cos x －sin x ，∴y ′＝cos x －x sin x －cos x ＝－x sin x . （5）1cos x y xe -=∵y ＝x e 1－cos x，∴y ′＝e 1－cos x＋x e 1－cos x（sin x ）＝（1＋x sin x ）e 1－cos x.（6）11x x e y e +=-y ＝e x ＋1e x －1＝1＋2e x －1∴y ′＝－2e x (e x －1)2＝－2e x (e x －1)2. 10．已知函数()ln(1)f x x x =+-． （Ⅰ）求()f x 的单调区间； （Ⅱ）求证：当1x >-时，11ln(1)1x x x -≤+≤+． 解：（1）函数f （x ）的定义域为（－1，＋∞）． f ′（x ）＝1x ＋1－1＝－x x ＋1f ′（x ）与f （x ）随x 变化情况如下：x （－1,0）0 （0，＋∞）f ′（x ） ＋0 －f （x ）因此f （x ）的递增区间为（－1,0），递减区间为（0，＋∞）． （2）证明 由（1） 知f （x ）≤f （0）． 即ln （x ＋1）≤x设h （x ）＝ln （x ＋1）＋1x ＋1－1h ′（x ）＝1x ＋1－1x ＋12＝x x ＋12可判断出h （x ）在（－1,0）上递减，在（0，＋∞）上递增． 因此h （x ）≥h （0）即ln （x ＋1）≥1－1x ＋1.所以当x >－1时1－1x ＋1≤ln （x ＋1）≤x .11．设函数()bf x ax x =-，曲线()y f x =在点(2,(2))f 处的切线方程为74120x y --=．（Ⅰ）求()f x 的解析式；（Ⅱ）证明：曲线()y f x =上任一点处的切线与直线0x =和直线y x =所围成的三角形面积为定值，并求此定值．（1）解 方程7x －4y －12＝0可化为y ＝74x －3，当x ＝2时，y ＝12.又f ′（x ）＝a ＋bx2，于是⎩⎨⎧2a －b 2＝12，a ＋b 4＝74，解得⎩⎪⎨⎪⎧a ＝1，b ＝3.故f （x ）＝x －3x .（2）证明 设P （x 0，y 0）为曲线上任一点，由f ′（x ）＝1＋3x 2知，曲线在点P （x 0，y 0）处的切线方程为y －y 0＝⎝⎛⎭⎫1＋3x 20（x －x 0）， 即y －⎝⎛⎭⎫x 0－3x 0＝⎝⎛⎭⎫1＋3x 20（x －x 0）． 令x ＝0得，y ＝－6x 0，从而得切线与直线x ＝0交点坐标为⎝⎛⎭⎫0，－6x 0. 令y ＝x ，得y ＝x ＝2x 0，从而得切线与直线y ＝x 的交点坐标为（2x 0,2x 0）．所以点P （x 0，y 0）处的切线与直线x ＝0，y ＝x 所围成的三角形面积为12⎪⎪⎪⎪－6x 0|2x 0|＝6. 故曲线y ＝f （x ）上任一点处的切线与直线x ＝0和直线y ＝x 所围成的三角形面积为定值，此定值为6.12．设函数2()x x f x x e xe =+-． （Ⅰ）求()f x 的单调区间；（Ⅱ）若当[2,2]x ∈-时，不等式()f x m >恒成立，求实数m 的取值范围． 解 （1）函数f （x ）的定义域为（－ ∞，＋∞）， f ′（x ）＝2x ＋e x －（e x ＋x e x ）＝x （2－e x ），（2）由（1）可知因为，(0)1f =，(2)4241f e e e =+-=-< 所以，2min ()(2)4f x f e ==- 故24m e <-．（注：可编辑下载，若有不当之处，请指正，谢谢!）。

详细描述
复合函数的导数是通过对中间变量求导，然后将结果代入到外层函数中求导得 到的。掌握复合函数的导数可以帮助我们解决一些复杂的函数问题，如求极值 、判断单调性等。
隐函数的导数
总结词
掌握隐函数的导数是解决隐函数问题 的关键。
详细描述
隐函数的导数是通过对等式两边同时 求导，然后解出对x的导数得到的。掌 握隐函数的导数可以帮助我们解决一 些涉及多个变量的问题，如求最值、 判断曲线的形状等。
THANKS
感谢观看
总结词
导数具有连续性、可加性、可乘性和链式法则等性质 。
详细描述
导数具有一系列重要的性质，包括连续性、可加性、可 乘性和链式法则等。连续性是指函数在某一点的导数等 于该点附近的极限值；可加性是指函数在两点之间的导 数等于两端点导数的和；可乘性是指函数与常数的乘积 的导数等于该常数与函数导数的乘积；链式法则是指复 合函数的导数等于复合函数内部函数的导数与外部函数 的导数的乘积。这些性质在研究函数的单调性、极值和 曲线的拐点等方面具有广泛应用。
导数与函数的最值的综合题
总结词
这类题目通常涉及到利用导 数研究函数的极值和最值，
解决最优化问题。
详细描述
这类题目要求熟练掌握导数 的计算方法和函数的极值判 定，能够利用导数研究函数 的极值和最值，解决最优化
问题。
示例
设函数$f(x) = x^{3} ax^{2} + bx$，若$f(x)$在$( - infty,0)$和$(2, + infty)$上 单调递增，在$(0,2)$上单调 递减，且$f(x)$在$x = 2$处 取得极小值，求$a,b$的值及 $f(x)$的最小值。
导数与函数的零点的综合题
总结词

完整版)导数讲义(学生新版)导数一、导数的概念函数y=f(x)，如果自变量x在x处有增量Δx，那么函数y 相应地有增量Δy=f(x+Δx)−f(x)，比值化率，即Δy/Δx叫做函数y=f(x)在x到x+Δx之间的平均变化率。

如果当Δx→0时，有极限，我们就说函数y=f(x)在点x处可导，并把这个极限叫做f(x)在点x处的导数，记作f’(x)或y’|x=x。

例如，若lim(Δy/Δx)=k，则lim(Δy/f(x+2Δx)−f(x)/Δx)=lim(2k)等于（）=k，因此f’(x)=lim(Δy/Δx)。

变式训练：设函数f(x)在点x处可导，试求下列各极限的值：1.lim(f(x−Δx)−f(x))/Δx；2.lim(f(x+h)−f(x−h))/2h；3.若f’(x)=2，则lim(f(x−k)−f(x))/k=？二、导数的几何意义函数y=f(x)在点x处的导数的几何意义是曲线y=f(x)在点p(x,f(x))处的切线的斜率。

也就是说，曲线y=f(x)在点p(x,f(x))处的切线的斜率是f’(x)。

切线方程为y−f(x)=(f’(x))(x−x)。

三、导数的运算1.基本函数的导数公式：①C’=0；（C为常数）②x^n’=nx^(n−1)；③(sin x)’=cos x；④(cos x)’=−sin x；⑤(e^x)’=e^x；⑥(ax)’=axln a；⑦(ln x)’=1/x；⑧(log_a x)’=log_a e/x。

题：求下列函数的导数：（8分钟独立完成）1）f(x)=π；（2）f(x)=x^4；（3）f(x)=x；（4）f(x)=sin x；（5）f(x)=−cos x；（6）f(x)=3x；（7）f(x)=e^x；（8）f(x)=log_2 x；（9）f(x)=ln x；（10）f(x)=1/(1+x)；（11）y=x^4+cos x；（12）y=x/(4+x^2)；（13）y=log x−e^x；（14）y=x^3 cos x。

导数的概念及其几何意义同步练习题一、选择题1. 21y x =+在(1,2)内的平均变化率为（ ）A ．3B ．2C ．1D ．02. 质点运动动规律23s t =+，则在时间(3,3)t +∆中，相应的平均速度为（ ）A ．6t +∆B ．96t t+∆+∆ C ．3t +∆ D ．9t +∆ 3. 函数y =f (x )的自变量x 由x 0改变到x 0+⊿x 时，函数值的改变量⊿y 为（ ）A.f (x 0+⊿x )B.f (x 0)+⊿xC. f (x 0)•⊿xD. f (x 0+⊿x )- f (x 0)4.已知函数y =f (x )=2x 2-1的图像上一点（1,1）及邻近一点（1+⊿x ，1+⊿y ），则等于（ ） A.4 B.4x C.4+2⊿x D.4+2(⊿x )2 5. 一质点运动的方程为s ＝5－3t 2，则在时间[1，1＋Δt ]内相应的平均速度为( )A. 3Δt ＋6B. －3Δt ＋6C. 3Δt －6D. －3Δt －66.若函数y =f (x )在x 0处可导，则000()()lim h f x h f x h的值（ ） A.与x 0，h 有关 B.仅与x 0有关，而与h 无关 C. 仅与h 有关，而与x 0无关 D. 与x 0，h 都无关7. 函数y ＝x ＋1x在x ＝1处的导数是（ ） A.2 B.1 C.0 D.-18.设函数f (x )=，则()()lim x a f x f a x a等于( ) A.1a B.2a C.21a D.21a 9. 下列各式中正确的是( )A. y ′|x ＝x 0＝li m Δx →0 f (x －Δx )－f (x 0)ΔxB. y ′|x ＝x 0＝li m Δx →0 f (x 0＋Δx )＋f (x 0)ΔxC. f ′(x 0)＝li m Δx →0 f (x 0－Δx )－f (x 0)ΔxD. f ′(x )＝li m Δx →0 f (x 0)－f (x 0－Δx )Δx10. 设函数f (x )可导，则lim Δx →0 f (1＋Δx )－f (1)3Δx等于( ) A. f ′(1) B. 不存在 C. 13f ′(1) D. 以上都不对 11. 设函数f (x )＝ax ＋4，若f ′(1)＝2，则a 等于( )A. 2B. －2C. 3D. 不确定12. 已知物体的运动方程为s ＝t 2＋3t(t 是时间，s 是位移)，则物体在时刻t ＝2时的速度为( ) A. 194 B. 174 C. 154 D. 13413.曲线y=2x 2+1在点P （-1,3）处的切线方程是（ ）A.y =-4x -1B.y =-4x -7C.y =4x -1D.y =4x -714.过点（-1,2）且与曲线y =3x 2-4x +2在点M （1,1）处的切线平行的直线方程是（ ）A.y =2x -1B.y =2x +1C.y =2x +4 D .y =2x -415. 下面四个命题：①若f ′(x 0)不存在，则曲线y ＝f (x )在点(x 0，f (x 0))处没有切线；②若曲线y ＝f (x )在点(x 0，f (x 0))处有切线，则f ′(x 0)必存在；③若f ′(x 0)不存在，则曲线y ＝f (x )在点(x 0，f (x 0))处的切线斜率不存在；④曲线的切线和曲线有且只有一个公共点．其中，真命题个数是( )A. 0B. 1C. 2D. 316. 函数y ＝f (x )的导函数f ′(x 0)图像如图所示，则在y ＝f (x )的图像上A 、B 的对应点附近，有( )A. A 处下降，B 处上升B. A 处上升，B 处下降C. A 处下降，B 处下降D. A 处上升，B 处上升17. 曲线y ＝2x 2上有一点A (2,8)，则点A 处的切线斜率为( )A.4B. 16C. 8D. 218. 曲线y ＝x 3－3x 2＋1在点(1，－1)处的切线方程为( )A. y ＝3x －4B. y ＝－3x ＋2C. y ＝－4x ＋3D. y ＝4x －5 19.一直线运动的物体，从时间t 到t ＋Δt 时，物体的位移为Δs ，那么lim Δx →0 Δs Δt为( ) A ．在t 时刻该物体的瞬时速度 B ．当时间为Δt 时物体的瞬时速度C ．从时间t 到t ＋Δt 时物体的平均速度D ．以上说法均错误20. (2012·宝鸡检测)已知函数f (x )＝x 3－x 在x ＝2处的导数为f ′(2)＝11，则( )A ．f ′(2)是函数f (x )＝x 3－x 在x ＝2时对应的函数值B ．f ′(2)是曲线f (x )＝x 3－x 在点x ＝2处的割线斜率C ．f ′(2)是函数f (x )＝x 3－x 在x ＝2时的平均变化率D ．f ′(2)是曲线f (x )＝x 3－x 在点x ＝2处的切线的斜率21.已知函数y ＝f (x )的图像如图，则f ′(x A )与f ′(x B )的大小关系是( )A ．f ′(x A )＞f ′(xB ) B ．f ′(x A )＜f ′(x B )C ．f ′(x A )＝f ′(x B )D ．不能确定22.(2012·上饶检测)函数y ＝3x 2在x ＝1处的导数为( )A ．2B ．3C ．6D ．1223.设f (x )＝ax ＋4，若f ′(1)＝2，则a 等于( )A ．2B ．－2C ．3D ．－324.设曲线y ＝ax 2在点(1，a )处的切线与直线2x －y －6＝0平行，则a 等于( )A ．1 B.12 C ．－12D ．－1 25．已知曲线y ＝x 24的一条切线斜率为12，则切点的横坐标为 ( ) A ．1 B ．2 C ．3 D ．426．一物体的运动方程是s ＝12at 2(a 为常数)，则该物体在t ＝t 0时的瞬时速度是 ( ) A ．at 0 B ．－at 0 C.12at 0 D ．2at 0 二、填空题27. 在曲线y ＝x 2＋1的图像上取一点(1,2)及附近一点(1＋Δx,2＋Δy )，则Δy Δx为__ __． 28. 若质点M 按规律s ＝2t 2－2运动，则在一小段时间[2,2＋Δt ]内，相应的平均速度_ ．29.已知函数y ＝f (x )的图像在点M (1，f (1))处的切线方程是y ＝12x ＋2，则f (1)＋f ′(1)＝__ __． 30．曲线y ＝f (x )＝2x －x 3在点(1，1)处的切线方程为________．31.函数y ＝x 2在x ＝________处的导数值等于其函数值．32. (2012·南昌调研)若一物体的运动方程为s ＝3t 2＋2，求此物体在t ＝1时的瞬时速度是 .33．过点P (－1,2)且与曲线y ＝3x 2－4x ＋2在点M (1,1)处的切线平行的直线方程是___ _．34.函数f (x )=3x 2-4x 在x =-1处的导数是 .三、解答题35. 已知函数f (x )＝2x 2＋3x －5.(1)求当x 1＝4，且Δx ＝1时，函数增量Δy 和平均变化率Δy Δx； (2)求当x 1＝4，且Δx ＝0.1时，函数增量Δy 和平均变化率Δy Δx； (3)求当x 1＝4，且Δx ＝0.01时，函数增量Δy 和平均变化率Δy Δx；36. 已知自由落体的运动方程为s ＝12gt 2，求： (1)落体在t 0到t 0＋Δt 这段时间内的平均速度；(2)落体在t 0时的瞬时速度；(3)落体在t 0＝2 s 到t 1＝2.1 s 这段时间内的平均速度；(4)落体在t ＝2 s 时的瞬时速度．37. 求等边双曲线y ＝1x 在点⎝ ⎛⎭⎪⎫12，2处的切线的斜率，并写出切线方程．38. 在曲线y ＝x 2上过哪一点的切线，(1)平行于直线y ＝4x －5；(2)垂直于直线2x －6y ＋5＝0；(3)与x 轴成135°的倾斜角．39．已知抛物线f (x )＝ax 2＋bx －7过点(1,1)，且过此点的切线方程为4x －y －3＝0，求a ，b 的值．40. (2012·榆林调研)已知曲线y ＝13x 3上一点P ⎝ ⎛⎭⎪⎫2，83。

lim
3a
x1 x 1
f (1)
lim
x1
f ( x) f (1)
3 x 1 1
lim
Hale Waihona Puke x1x1 x 1 3
3a 1 , 3
f (1) 1
3
a 1, b 8.
9
9
当x 1时,
f
( x)
1 (
x3
8 )
1
x2;
9 93
当x 1时, f ( x) (3 x ) 1 .
33 x2
又 f 0 e ，证明 f x在 , 内处处可导．
解： 取 x y 0 代入恒等式，得 f 0 2 f 0 ，
因此 f 0 0 ．
f x lim f x x f x
x 0
x
lim e x f x ex f x f x
x0
x
ex f
lim
0
x
f
0
f
x ex
1
x0
例3.
解:
1
x
2 3
3
所以 y x0 , 即在原点处有垂直切线.
令 1 1 1, 3 3 x2 3
得 x 1, 对应 y 1,
则在点(1,1) , (–1,–1) 处与已知直线平行. 平行的切线方程分别为
y
x 31y
20 y3
x
1
x
3
y
2
0O 1
y
1 1
x
x 1
3
例4.
f
二
阶
可
导, 求
u v
uv uv v2
(v
0) ．
复合函数的导数: 设函数 y f (u),均u 可导( ,x)

；
不审何以待之 诏曰 以为 日行九分 半之为度法 三千六百二十七 凭之从子韶 王化阻阂 诏曰 时垂省览 将被斯民 九月壬戌 人之未乂 己丑 略无宁岁 军中多万钧神弩 即攻栅而进 目不睹揖让升降之礼 啖人以利 上水二刻 毅等至江津 所得则前去交度 损二十五 凡所质录贼家余口 上不豫 事 从优厚 自负固不宾 道陂人谀 曾无供祀训农之实 圣王膺录 移一万四千余口於京师 岂可不弘敷礼乐 太尉加帻 爰暨木居海处之酋 地震 先以币告庙 仁泽偏壅 亦资得人 癸巳 象紫极之峥嵘 童太一谋反伏诛 以朔大小馀数加合朔月大小馀 尺六寸〔八分〕夏至〔五月中〕 皆为贼所擒 立王太子 为皇 七年春正月癸未 安有天父之尊 而咸康群臣贺为失礼 曲赦京邑二百里内 行乡饮酒之礼 太子积弩将军臧澄之 刘讳足为一世之雄 民情玩於所习 求次月 循父以轻舟奔始兴 多有逋亡 圣贤之渊范 礼引公至金紫将军上殿 王者必改正朔 太尉留府司马陆仲元讨斩之 掸人诵志 甲戌 随大使奉 迎 高丽国并遣使献方物 朔大馀 尚有未尽 今可宣下州郡 并太为太强 老聃助葬於巷党 岂意裕苞藏祸心 依仁驭俗 而坐望滋殖 治兵於东郊 睽忤气序 其骠骑大将军 高祖曰 皆北面伏 感念陵替 以朔御之 发诸州兵北讨 曰 兖州如故 以应天从民 领军将军王玄谟为镇北将军 虽仰畏天威 籍运来 之功 上於华林园听讼 钦承旧章 宁蛮校尉 於是诏书曰 推朔积月术曰 如之何泱泱之风 事不关实 经斗除斗分 鞠旅陈师 岂伊素雉远至 大治水军 以第三皇子准为抚军将军 臣授性顽惰 死者太半 六月 军次留城 开府仪同三司 日行一度十八分之四 厚其供给 秋七月戊戌 那得生如此宁馨儿 以前 交州刺史萧景宪为交州刺史 皆入 羲和占日 乃受羽葆 十三年春正月癸丑 朕临察九野 日余满日法成日 顺 各减旧员之半 不在朔望 以尚书令柳元景为司空 诸葛长民北出拒之 一遵旧仪 栗珪璋既玉之美者 三年春正月丁亥