尺寸链计算方法
- 格式:docx
- 大小:114.04 KB
- 文档页数:12

尺寸链概率法计算公式
尺寸链是指由不同大小的尺寸组成的链条,通常会按照其中一种规则进行排序,比如从大到小或从小到大。
在实际应用中,尺寸链可以用来描述一系列不同尺寸的物体、事件或数据,比如排行榜、尺码表或者网络结构。
P(x) = P(x1) * P(x2,x1) * P(x3,x2) * ... * P(xn,xn-1)
其中,P(x)表示整个尺寸链的概率,P(xi)表示第i个尺寸的概率,P(xi,xi-1)表示第i个尺寸在已知前一个尺寸的条件下的概率。
1.收集数据:收集尺寸链中各个尺寸的数据,比如物体的大小、事件发生的概率或者数据的分布情况。
2.计算单个尺寸的概率:根据收集到的数据,计算每个尺寸出现的概率。
可以使用频率方法,通过统计尺寸出现的次数来计算概率,也可以使用概率密度方法,通过拟合尺寸的分布来计算概率。
3.计算条件概率:对于每个尺寸,计算它在已知前一个尺寸的条件下的概率。
可以使用条件概率密度方法,通过拟合条件概率分布来计算条件概率。
4.计算尺寸链的概率:根据计算得到的单个尺寸概率和条件概率,使用尺寸链概率计算公式计算整个尺寸链的概率。
尺寸链概率法的应用范围广泛,可以用于各种尺寸链的计算,比如排行榜的排序概率、尺码表的尺寸分布概率或者网络节点的连接概率等。
在实际应用中,需要使用适当的数据收集和计算方法来得到准确的概率值,以提高尺寸链模型的预测能力。
总之,尺寸链概率法是一种基于尺寸链模型的计算方法,通过计算单个尺寸和条件概率来确定整个尺寸链的概率。
它可以用于各种尺寸链的计算,为我们理解和应用尺寸链提供了有力的工具。

尺寸链计算方法及步骤尺寸链计算方法是在工程和设计领域中用来确定产品尺寸的一种方法。
通过尺寸链计算,可以确保产品的各个组成部分之间的尺寸关系符合设计要求,从而实现功能和装配的有效性。
下面将介绍尺寸链计算的具体方法及步骤。
一、确定设计要求在进行尺寸链计算之前,首先需要明确产品的设计要求。
这包括产品的功能要求、装配要求、尺寸公差要求等。
只有明确了这些设计要求,才能够有针对性地进行尺寸链计算。
二、确定尺寸链的起点和终点尺寸链计算中,需要确定尺寸链的起点和终点。
起点是指一个确定的尺寸基准,终点是指产品中的某个关键尺寸。
起点和终点之间的尺寸关系将通过尺寸链计算得出。
三、确定尺寸链的路径确定尺寸链的路径是指确定起点和终点之间的尺寸关系路径。
这个路径通常是通过产品的装配关系来确定的。
在确定路径时,需要考虑产品的功能和装配要求,确保路径的合理性和有效性。
四、确定尺寸链各个环节的尺寸公差尺寸链计算中,每个环节都有一定的尺寸公差。
尺寸公差是指在设计和生产过程中,为了满足产品功能和装配要求而允许的尺寸偏差范围。
确定尺寸链各个环节的尺寸公差需要考虑产品的功能要求和装配要求,确保尺寸链的有效性和可控性。
五、计算尺寸链各个环节的尺寸在确定了尺寸链的路径和尺寸公差之后,就可以开始计算尺寸链各个环节的尺寸了。
计算尺寸时,需要考虑尺寸公差和装配要求,确保尺寸的准确性和一致性。
六、验证尺寸链的有效性计算完成后,需要对尺寸链进行验证,确保其满足设计要求和装配要求。
验证的方法可以采用数值模拟、实验测试等手段。
通过验证,可以判断尺寸链的有效性,及时发现和解决尺寸关系的问题。
七、优化尺寸链在进行尺寸链计算的过程中,可能会发现一些尺寸关系不符合设计要求或装配要求。
在这种情况下,需要对尺寸链进行优化,调整尺寸关系,使其满足要求。
优化尺寸链的方法可以包括调整尺寸公差、改变尺寸关系路径等。
八、更新尺寸链计算结果在完成尺寸链计算和优化之后,需要及时更新尺寸链计算结果。

尺寸链概率法计算一、尺寸链概率法简介尺寸链概率法是一种用于评估产品尺寸和形状公差的方法,通过对产品各尺寸的误差进行概率统计分析,得出符合规格的概率。
这种方法在我国制造业中得到了广泛的应用,为企业提高了产品质量,降低了成本。
二、尺寸链概率法计算原理尺寸链概率法的计算原理是基于概率论和数理统计。
首先,对产品各尺寸的测量数据进行收集和整理,然后计算各尺寸的偏差,接着根据尺寸偏差的大小和分布,计算各个尺寸符合规格的概率。
三、尺寸链概率法计算步骤1.收集产品各尺寸的测量数据。
2.计算各尺寸的偏差。
3.分析尺寸偏差的大小和分布,确定符合规格的概率。
4.计算各个尺寸链的概率。
5.根据概率值,评估产品的尺寸和形状公差。
四、实例分析以一款手机为例,对其长度、宽度和厚度三个尺寸进行尺寸链概率法计算。
首先收集手机各尺寸的测量数据,然后计算各尺寸的偏差。
通过分析尺寸偏差的大小和分布,得出符合规格的概率。
最后,根据概率值评估手机的尺寸公差,为企业提供改进产品质量的依据。
五、应用场景及优势尺寸链概率法适用于各种制造业,特别是对于大批量生产的产品,可以有效地提高产品质量,降低成本。
其优势如下:1.提高产品质量:通过概率法计算,企业可以更准确地掌握产品尺寸和形状公差的状况,从而有针对性地改进生产过程。
2.降低成本:尺寸链概率法可以帮助企业优化生产资源配置,减少因产品质量问题导致的返工、退货等额外成本。
3.提高客户满意度:尺寸链概率法有助于提高产品的一致性和可靠性,使客户获得更好的使用体验。
六、总结尺寸链概率法作为一种有效的产品质量评估方法,在制造业中具有重要应用价值。
通过对产品尺寸和形状公差的概率统计分析,企业可以更好地掌握产品质量状况,从而提高产品质量和降低成本。

尺寸链的计算方法尺寸链(Size Chain)是一种用于计算产品尺寸的方法。
它通常应用于制造业中,用于确定产品的尺寸规格和控制尺寸变化的程度。
尺寸链的计算方法通常包括以下几个步骤:1.确定产品的需求和要求:在开始计算尺寸链之前,首先需要明确产品的需求和要求,包括外观和性能等方面。
这包括与客户和设计师沟通,以确保产品尺寸链的计算符合其期望。
2.收集尺寸数据:通过测量和记录产品的关键尺寸数据,包括长度、宽度、高度、深度、直径等。
这些数据将用于计算尺寸链的各个参数。
3. 计算起始尺寸(Baseline):起始尺寸是指产品的基准尺寸,即在制造过程中不发生任何尺寸变化时的尺寸。
可以根据客户的要求或产品设计文档中的规格来确定起始尺寸。
4.确定各个工序的尺寸变化:对于产品制造过程中涉及尺寸变化的每个工序,需要确定其对产品尺寸的影响程度。
这可以通过实验、模拟或经验来获取相关数据。
例如,在注塑成型过程中,温度、压力和材料流动性等因素都会影响最终产品的尺寸。
5. 计算尺寸链参数:根据各个工序的尺寸变化数据,可以计算出尺寸链的各个参数,包括尺寸链比例(Size Chain Ratio)和尺寸链统计(Size Chain Statistics)等。
尺寸链比例表示每个工序中尺寸变化的幅度与起始尺寸之间的比例关系。
尺寸链统计表示在整个制造过程中尺寸变化的累积情况。
6.分析和优化尺寸链:一旦计算出尺寸链的参数,可以对其进行分析和优化。
通过对尺寸链数据的统计和分析,可以确定影响尺寸变化的主要因素,并采取相应的措施来减小尺寸变化的幅度,提高产品的尺寸一致性和质量稳定性。
7.应用尺寸链于生产控制:尺寸链的计算结果可以应用于产品的生产控制和质量管理中。
例如,在制造过程中可以设置尺寸监测点,对产品进行尺寸测量,并与尺寸链数据进行比较,以确保产品尺寸处于可接受的范围内。
如果发现尺寸偏差过大,可以及时调整制造参数,纠正尺寸偏差,以保证产品质量。

尺寸链(dimension chain)计算是在工程和制造领域中常用的方法,用于计算物体的尺寸或特征之间的关系。
以下是尺寸链计算中常用的四个公式:
1.长度链:长度链用于计算物体的长度或距离之间的关系。
常见的长度链公式如下:
L = L₁ + L₂ + L₃ + … + Ln
其中,L 表示总长度或距离,L₁、L₂、L₃等表示各个部分的长度或距离。
2.半径链:半径链用于计算物体的半径或直径之间的关系。
常见的半径链公式如下:
R = R₁ + R₂ + R₃ + … + Rn
或
D = 2R = 2(R₁ + R₂ + R₃ + … + Rn)
其中,R 表示总半径或直径,R₁、R₂、R₃等表示各个部分的半径或直径。
3.弧长链:弧长链用于计算物体的弧长之间的关系。
通常以角度来度量弧长,常见的弧长链公式如下:
S = S₁ + S₂ + S₃ + … + Sn
其中,S 表示总弧长,S₁、S₂、S₃等表示各个部分的弧长。
4.面积链:面积链用于计算物体的面积之间的关系。
常见的面积链公式如下:
A = A₁ + A₂ + A₃ + … + An
其中,A 表示总面积,A₁、A₂、A₃等表示各个部分的面积。
这些公式表示了尺寸链计算中常见的关系,可用于计算和预测物体的尺寸或特征。
在实际应用中,具体的公式和计算方式可能会根据实际情况和所涉及的几何形状而有所变化。

一、尺寸链及尺寸链计算公式1、尺寸链的定义在工件加工和机器装配过程中,由相互联系的尺寸,按一定顺序排列成的封闭尺寸组,称为尺寸链。
尺寸链示例2、工艺尺寸链的组成环:工艺尺寸链中的每一个尺寸称为尺寸链的环。
工艺尺寸链由一系列的环组成。
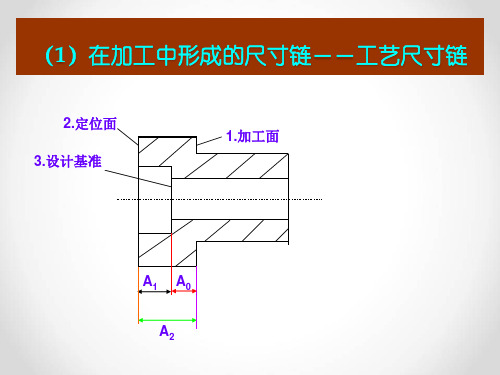
环又分为:(1)封闭环(终结环):在加工过程中间接获得的尺寸,称为封闭环。
在图b所示尺寸链中,A0是间接得到的尺寸,它就是图b所示尺寸链的封闭环。
(2)组成环:在加工过程中直接获得的尺寸,称为组成环。
尺寸链中A1与A2都是通过加工直接得到的尺寸,A1、A2都是尺寸链的组成环。
1)增环:在尺寸链中,自身增大或减小,会使封闭环随之增大或减小的组成环,称为增环。
表示增环字母上面用--> 表示。
2)减环:在尺寸链中,自身增大或减小,会使封闭环反而随之减小或增大的组成环,称为减环。
表示减环字母上面用<-- 表示。
3)怎样确定增减环:用箭头方法确定,即凡是箭头方向与封闭环箭头方向相反的组成环为增环,相同的组成环为减环。
在图b所示尺寸链中,A1是增环,A2是减环。
4)传递系数ξi:表示组成环对封闭环影响大小的系数。
即组成环在封闭环上引起的变动量对组成环本身变动量之比。
对直线尺寸链而言,增环的ξi=1,减环的ξi=-1。
3.尺寸链的分类4.尺寸链的计算尺寸链计算有正计算、反计算和中间计算等三种类型。
已知组成环求封闭环的计算方式称作正计算;已知封闭环求各组成环称作反计算;已知封闭环及部分组成环,求其余的一个或几个组成环,称为中间计算。
尺寸链计算有极值法与统计法(或概率法)两种。
用极值法解尺寸链是从尺寸链各环均处于极值条件来求解封闭环尺寸与组成环尺寸之间关系的。
用统计法解尺寸链则是运用概率论理论来求解封闭环尺寸与组成环尺寸之间关系的。
5.极值法解尺寸链的计算公式(4)封闭环的中间偏差(5)封闭环公差(6)组成环中间偏差Δi=(ES i+EI i)/2(7)封闭环极限尺寸(8)封闭环极限偏差6.竖式计算法口诀:封闭环和增环的基本尺寸和上下偏差照抄;减环基本尺寸变号;减环上下偏差对调且变号。


尺寸链的计算方法
尺寸链是指产品设计、制造、装配和质量控制过程中的一种重要工具,它可以
帮助我们更好地理解产品的尺寸要求,保证产品的质量和性能。
在实际工程中,尺寸链的计算方法是非常关键的,下面我们将详细介绍尺寸链的计算方法。
首先,我们需要明确尺寸链的定义。
尺寸链是指产品各零部件之间的尺寸关系,包括公差、配合、间隙等内容。
在产品设计阶段,我们需要根据产品的功能要求和制造工艺来确定尺寸链,以保证产品的装配性和性能。
其次,尺寸链的计算方法主要包括以下几个步骤,确定尺寸链的起始尺寸、确
定尺寸链的公差、计算尺寸链的累积公差、分析尺寸链的影响。
首先,我们需要根据产品的功能要求和装配工艺确定尺寸链的起始尺寸,即各零部件的基准尺寸。
然后,根据国家标准或行业标准确定各零部件的公差,包括尺寸公差、形位公差等。
接下来,我们需要计算尺寸链的累积公差,即各零部件在装配过程中的尺寸偏差累积值。
最后,我们需要分析尺寸链对产品性能和装配性的影响,以确定是否满足产品设计要求。
在实际工程中,尺寸链的计算方法需要结合产品的具体情况和制造工艺来进行。
我们需要根据产品的功能要求和装配工艺来确定尺寸链的起始尺寸和公差,同时考虑产品的材料特性和加工工艺,以保证产品的质量和性能。
总之,尺寸链的计算方法是产品设计和制造过程中的重要内容,它可以帮助我
们更好地理解产品的尺寸要求,保证产品的质量和性能。
在实际工程中,我们需要根据产品的具体情况和制造工艺来确定尺寸链,以保证产品的装配性和性能。
希望本文对您有所帮助,谢谢阅读!。

尺寸链计算方法及案例详解尺寸链计算方法是指根据产品的尺寸要求和特定的工艺流程,通过一系列的计算和分析来确定产品各个部件的尺寸和配合关系的方法。
尺寸链计算方法主要应用于机械设计、工程制图、零部件加工等领域,是确保产品尺寸精度和装配质量的重要手段。
首先,尺寸链计算方法需要明确产品设计的功能要求和工艺要求,包括产品的使用环境、受力情况、材料特性等。
然后,根据这些要求,确定产品各个部件之间的配合关系和尺寸范围。
接着,通过计算和分析,确定各个部件的尺寸,并建立尺寸链,保证各个部件在装配时能够满足设计要求。
在实际应用中,尺寸链计算方法通常涉及到几个方面的内容,包括尺寸配合计算、公差分配、尺寸链分析等。
在尺寸配合计算中,需要根据配合要求和公差要求,确定配合尺寸的上限和下限。
公差分配则是根据产品功能和装配要求,合理地分配公差,确保产品的性能和装配质量。
尺寸链分析则是通过建立尺寸链图,分析各个部件之间的尺寸关系,找出影响产品尺寸精度的关键因素,从而指导产品设计和加工。
举个简单的案例来说明尺寸链计算方法的应用。
比如,某机械零件的装配要求是要求两个轴承孔的中心距离在一定范围内,并且轴承孔的直径要求在一定的公差范围内。
在这种情况下,就需要通过尺寸链计算方法来确定轴承孔的尺寸和配合关系。
首先根据轴承的尺寸和公差要求,确定轴承孔的上限和下限尺寸。
然后根据轴承孔的位置和受力情况,确定轴承孔中心距离的范围。
最后通过尺寸链计算方法,确定轴承孔的尺寸和配合关系,以保证产品的装配质量和性能。
总之,尺寸链计算方法是一种重要的工程技术方法,通过合理的计算和分析,能够确保产品的尺寸精度和装配质量,对于提高产品的质量和竞争力具有重要意义。

第十章装配精度与加工精度分析任何机械产品及其零部件的设计,都必须满足使用要求所限定的设计指标,如传动关系、几何结构及承载能力等等;此外,还必须进行几何精度设计;几何精度设计就是在充分考虑产品的装配技术要求与零件加工工艺要求的前提下,合理地确定零件的几何量公差;这样,产品才能获得尽可能高的性能价格比,创造出最佳的经济效益;进行装配精度与加工精度分析以及它们之间关系的分析,可以运用尺寸链原理及计算方法;我国业已发布这方面的国家标准GB5847—86尺寸链计算方法,供设计时参考使用;第一节尺寸链的基本概念一、有关尺寸链的术语及定义1.尺寸链在机器装配或零件加工过程中,由相互连接的尺寸形成的封闭尺寸组,称为尺寸链;尺寸链分为装配尺寸链和工艺尺寸链两种形式;a齿轮部件b尺寸链图c尺寸链图图10-1 装配尺寸链示例图10-1a为某齿轮部件图;齿轮3在位置固定的轴1上回转;按装配技术规范,齿轮左右端面与挡环2和4之间应有间隙;现将此间隙集中于齿轮右端面与挡环4左端面之间,用符号A0表示;装配后,由齿轮3的宽度A1、挡环2的宽度A2、轴上轴肩到轴槽右侧面的距离A3、弹簧卡环5的宽度A4及挡环4的宽度A5、间隙A0依次相互连接,构成封闭尺寸组,形成一个尺寸链;这个尺寸链可表示为图10-1b与图10-1c两种形式;上述尺寸链由不同零件的设计尺寸所形成,称为装配尺寸链;图10-2a为某轴零件图局部;该图上标注轴径B1与键槽深度B2;键槽加工顺序如图10-2b所示:车削轴外圆到尺寸C1,铣键槽深度到尺寸C2,磨削轴外圆到尺寸C3即图10-2a中的尺寸B1 ,要求磨削后自然形成尺寸C0即图10-2a中的键槽深度尺寸B2;在这个过程中,加工尺寸C1、C2、C3和完工后尺寸C0构成封闭尺寸组,形成一个尺寸链;该尺寸链由同一零件的几个工艺尺寸构成,称为工艺尺寸链;a轴零件图局部b铣键槽工艺顺序图c尺寸链图图10-2 工艺尺寸链示例2.环列入尺寸链中的每一个尺寸,称为环;环一般用大写英文字母表示;如图10-1b中的A0、A1、A2、A3、A4、A5,及图10-2c中的C0、C1/2、C2、C3/2皆是环;3.封闭环尺寸链中在装配过程或加工过程最后形成的一环称为封闭环;封闭环一般用加下标阿拉伯数字“0”的英文大写字母表示;如图10-1b、图10-1c中的A0和图10-2c 中的C0皆是封闭环;一个尺寸链只有一个封闭环;4.组成环尺寸链中对封闭环有影响的全部环称为组成环;这些环中任一环变动必然引起封闭环的变动;组成环一般用加下标阿拉伯数字除数字“0”外的英文大写字母表示;如图10-1b与图10-1c中的A1、A2、A3、A4、A5,及图10-2c中的C1/2、C2、C3/2皆是组成环;根据对封闭环的影响的不同,组成环分为增环与减环;(1)增环尺寸链中某组成环变动引起封闭环同向变动,则该组成环称为增环;同向变动指该环增大时封闭环也增大,该环减小时封闭环也减小;如图10-1b与图10-1c中的A3,图10-2c中的C2、C3/2皆是增环;(2)减环尺寸链中某组成环变动引起封闭环反向变动,则该组成环称为减环;反向变动指该环增大时封闭环减小,该环减小时封闭环增大;如图10-1b与图10-1c中的A1、A2、A4、A5,及图10-2c中的C1/2皆是减环;5.传递系数表示各组成环对封闭环影响大小的系数;用符号表示;二、尺寸链的形式按形成尺寸链的各环在空间所处位置,尺寸链可分为以下三种形式:1.直线尺寸链全部组成环皆平行于封闭环的尺寸链,称为直线尺寸链;直线尺寸链中增环的传递系数=+1,减环的传递系数=-1;以上两例皆属于直线尺寸链;2.平面尺寸链全部组成环位于一个或几个平行平面内,但某些组成环不平行于封闭环的尺寸链,称为平面尺寸链,如图10-3所示;a箱体b平面尺寸链图图10—3 箱体的平面尺寸链3.空间尺寸链组成环位于几个不平行平面内的尺寸链,称为空间尺寸链;必须指出,直线尺寸链是最常见的尺寸链,而平面尺寸链和空间尺寸链通常可以用空间坐标而平面尺寸链和空间尺寸链通常可以用空间坐标投影的方法转换为直线尺寸链,然后采用直线尺寸链的计算方法来计算;故本章只阐述直线尺寸链三、尺寸链的建立根据产品的装配技术要求或零件的加工过程所要求保证的某个尺寸精度,分析产品装配图上零件、部件之间的尺寸和位置关系,或分析零件加工过程中形成的各个尺寸,来建立尺寸链;正确建立尺寸链是十分重要的;尺寸链的建立可按以下步骤进行:1.确立封闭环装配尺寸链中的封闭环,是产品装配图上注明的装配技术要求所限定的那个尺寸;它是在装配过程中最后自然形成的;工艺尺寸链中的封闭环和组成环,都是在加工顺序确定后才能加以确定的;其封闭环是加工过程中最后自然形成的;2.查明组成环对于装配尺寸链:从与封闭环一侧相毗连的零件开始,依次找出与封闭环有直接影响直到与封闭环另一侧相毗连零件的有关尺寸为止,其中每个尺寸皆是组成环;对于工艺尺寸链:从封闭环一侧开始,按加工先后顺序,依次地找出与封闭环有直接影响的有关尺寸,一直到与封闭环的另一侧相连接为止,其中每个尺寸皆是组成环;3.画尺寸链图尺寸链可以画在结构简单的产品示意装配图上,如图10-1b所示;也可以用简单的尺寸关系表示,用带双箭头的线段表示尺寸链的各环;例如图10-1c、图10-2c 所示;必须指出,当尺寸链中某环是对称尺寸时,有时按原尺寸取半值画在图上;例如,图10-2c中的C1/2及C3/2;四、尺寸链的计算尺寸链的计算是指计算封闭环与组成环的基本尺寸和极限偏差;尺寸链的计算可分为设计计算与校核计算两类;1.设计计算设计计算是指已知封闭环的基本尺寸与极限偏差,以及各组成环的基本尺寸,计算各组成环的极限偏差;通常由设计人员在产品设计过程中,决定零件尺寸公差与形位公差时进行这种计算,它属于公差分配问题;2.校核计算校核计算是指已知所有组成环的基本尺寸和极限偏差,计算封闭环的基本尺寸和极限偏差;通常由设计者在审图时或者由工艺人员在产品投产前,根据工艺条件与现场获得的统计数据进行这种计算,它属于公差控制问题;五、封闭环与组成环基本尺寸的关系参看图10-4,多环直线尺寸链封闭环的基本尺寸等于各组成环基本尺寸中,所有增环尺寸之和与所有减环基本尺寸之和的差值;用10—1式表示如下:L 0=∑=l 1Z LZ -∑+=m 1l j L j 10—1式中 L 0 —— 封闭环基本尺寸;L z —— 增环基本尺寸;L j —— 减环基本尺寸;m —— 组成环环数;l —— 增环环数;图10-4 多环直线尺寸链图为保证封闭环的公差要求,可以采用完全互换法或大数互换法进行尺寸链计算;第二节 用完全互换法计算尺寸链完全互换法是指在全部产品中,装配时各组成环不需挑选或者改变其大小或位置,装入后即能达到封闭环的公差要求,以实现产品互换的尺寸链计算方法;该方法采用极值公差公式计算;一、完全互换法的计算公式1.封闭环与组成环极限尺寸的关系参看图10-4,当全部增环皆为其最大极限尺寸且全部减环皆为其最小极限尺寸时,则封闭环为其最大极限尺寸L 0max ;而在全部增环皆为其最小极限尺寸且全部减环皆为其最大极限尺寸时,则封闭环为其最小极限尺寸L 0min ;这种关系,可用下式表示:L 0ma x =∑=l 1z L Z max -∑+=m 1l j L j min 10-2L 0min =∑=l 1z L Z min -∑+=m 1l j L j ma x 10-3式中,z 和j 分别表示增环和减环,m 和l 分别表示组成环和增环的数目,L max 和L min 分别表示最大、最小极限尺寸;相应地,封闭环的上、下偏差ES 0、EI 0与组成环上、下偏差的关系如下: ES 0=∑=l z zES 1-∑+=m l j j EI 1 10-4EI 0=∑=l 1z EI Z -∑+=m 1l j ES j 10-5即:封闭环上偏差ES 0,等于所有增环上偏差ES z 之和减去所有减环下偏差EI j 之和所得的代数差;封闭环下偏差EI 0,等于所有增环下偏差EI z 之和减去所有减环上偏差ES j 之和所得的代数差;2.封闭环与组成环公差的关系将式10-2减去式10-3,得出封闭环公差T 0与各组成环公差T i 的关系如下: T 0=L 0max -L 0min=∑=l 1z Z T+∑+=m 1l j j T =∑=m 1i i T 10—6 式中,m 表示组成环数目; T z 表示增环公差; T j 表示减环公差;由式10-6知:尺寸链中封闭环公差等于所有组成环公差之和;该公式称为极值公差公式;由式10-6可知:尺寸链各环公差中封闭环的公差最大,所以,封闭环是尺寸链中精度最低的环;在当封闭环公差一定的条件下,组成环的环数越多,则各组成环的公差就越小;因此,在进行产品设计或零件加工工艺设计时,应尽量减少相关零件数或加工环节,即应尽量减少组成环的环数;这一原则叫“最短尺寸链”原则;一、设计计算已知封闭环的基本尺寸与极限偏差及组成环的基本尺寸,求各组成环的极限偏差;计算步骤如下:1.确定各组成环的公差首先,假设各组成环的公差都相等,即T 1=T 2=…=T m =T av ,L T av,L 为各组成环的平均公差;由式10-6得:T 0=mT av ,L因此,各组成环的平均公差用下式计算:T av ,L = T 0 /m 10-7然后,在此基础上调整各组成环的公差;如按组成环基本尺寸的大小来调整,则对于处于同一尺寸分段的组成环,取相同的公差值;也可按加工难易程度来调整,则对于加工容易的组成环,公差应减小,对于加工困难的组成环,公差应增大;调整后各组成环公差之和不得大于封闭环公差;2.确定组成环的极限偏差由封闭环公差确定各组成环公差后,可以按“偏差入体原则”或按“偏差对称”原则确定各组成环的极限偏差;对于内尺寸按H 配置,对于外尺寸按h 配置;对于一般长度尺寸按js 配置;然后,按式10-4和式10-5确定剩下一个组成环的极限偏差; 参看图10-1所示的齿轮部件及其尺寸链图;已知:各组成环的基本尺寸A 1=30mm,A 2=A 5=5mm,A 3=43mm,组成环A 4是标准件,A 4=3005.0- mm;要求装配后齿轮右端的间隙在~之间,试用完全互换法计算尺寸链,确定各组成环的极限偏差;解:本例中的装配技术要求间隙应在~范围内可用封闭环尺寸A 0=035.010.0++ mm 表示;组成环环数m =5,A 3为增环,A 1、A 2、A 4和A 5均为减环;封闭环公差T 0=0+-0+=;首先,按式10-7确定各组成环的平均公差为T av ,L = T 0 / m = / 5 =然后调整各组成环的公差;对尺寸较大、加工较难的组成环A 1、A 3应分配给较大公差;对尺寸较小的组成环A 2、A 5分配较小的公差值;按各组成环公差之和不得大于封闭环公差的原则,调整后得T 1=, T 2= T 5=,T 3=和T 4=;最后,确定各组成环的极限偏差;先按“偏差入体”原则确定A 1、A 2、A 5和A 4的极限偏差,这四个组成环的尺寸为:A 1=300 062.0- mm,A 2=A 5= 50 03.0- mm,A 4=30 05.0- mm;再由式10-4和10-5计算剩下一个组成环A 3的极限偏差,得:A 3=43178.0100.0++ mm;将所确定的五个组成环的极限尺寸,用式10-2和10-3核算封闭环极限尺寸, A 0max = A 3max –A 1min +A 2min +A 4min +A 5min= A 0min = A 3min –A 1max +A 2max +A 4max +A 5max= =+能够满足设计要求;例 2 参看图10-2b 所示的轴及其键槽加寸和设计尺寸,图10-2c 所示的尺寸链图,已知:车削加工尺寸C 1=0 1.0-,磨削加工尺寸C 3=700 06.0-mm,完工后键槽深度C 0=620 3.0- mm,试确定铣削键槽的深度C 2;本例中,依次加工C 1 、C 2 和C 3尺寸后,自然形成C 0,故C 0为尺寸链的封闭环;本例的计算为,已知封闭环极限尺寸与尺寸链中部分组成环的极限尺寸,求解剩下那个组成环的极限尺寸;解:分析图10-2c 所示的尺寸链图,判断C 2 和C 3/2为增环,C 1/2为减环;首先,由式10-1计算组成环C 2 的基本尺寸,得:C 2 = C 0 -C 3/2+C 1/2=62-70/2+2=然后计算组成环C 2 的极限偏差;因尺寸链中C 1和C 3取半值,故其极限偏差在尺寸链计算中应取半值;由式10-4、10-5计算得:ES 2 = ES 0- ES 3/2+ EI 1/2 =0-0+2=EI 2 = EI 0- EI 3/2+ ES 1/2 = 2+0=因此,铣削键槽的深度为:C 2 =05.027.0-- mm三、 校核计算已知全部组成环的基本尺寸和极限偏差,求封闭环的基本尺寸和极限偏差;用式10-1、10-2和式10-3进行计算;例3 图10-5a 为T 形导轨与滑块的配合图和零件尺寸、对称度公差标注图;已知导轨和滑块的尺寸分别为A 1=240.280 + mm 、 A 2=300.140 + mm 、A 3=230 28.0- mm 和A 4=3004.008.0-- mm,导轨小端中心平面相对于大端中心平面和滑块小端中心平面相对于大端中心平面的对称度公差分别为和;试计算当滑块与导轨大端在右侧接触时,滑块与导轨小端右侧和左侧之间的间隙A 01和A 02的变动范围;由图10-5a 可知:间隙A 01和A 02是在导轨与滑块装配后自然形成的,所以它们都是封闭环;由于滑块和导轨都具有对称性,因此在尺寸链图10-5b 与图10-5c 中,尺寸A 1、A 2、A 3和A 4皆取半值;此外,导轨和滑块各自的小端中心平面相对于大端中心平面的对称度误差对间隙A 01和A 02的大小均有影响;所以当它们的对称度公差如图10-5a 按独立原则标注时,应作为长度尺寸的组成环纳入尺寸链,并用A 5和A 6表示;写成极限尺寸形式为A 5=0和A 6=0;a T 形槽导轨与滑块b 滑块与导轨小端右侧间隙的尺寸链图c 滑块与导轨小端左侧间隙的尺寸链图 图10-5 导轨与滑块尺寸链⑴ 滑块与导轨小端右侧的间隙A 01的计算解:计算步骤如下:① 建立尺寸链图10-5b 的尺寸链图是这样画出的,从封闭环A 01的左端开始,经滑块小端尺寸A 3/2、A 6,再经滑块大端尺寸A 4/2至滑块与导轨大端接触处,然后经导轨大端尺寸A 2/2、A 5和导轨小端尺寸A 1/2与封闭环A 01的右端相接而成;分析该图知,A 1/2和A 4/2为增环,A 2/2、A 3/2、A 5和A 6为减环;应当指出,类似对称度这种基本尺寸为零且极限偏差对称配置的组成环,取为增环或减环皆可,效果相同;②计算封闭环A 01的基本尺寸:当A 1/2=1214.00 + mm 、A 2/2=1507.00 + mm 、A 3/2=0 14.0- mm 、A 4/2=15错误! mm 、A 5=±、A 6=±时按式10-1,得:A 01=A 1/2+ A 4/2-A 2/2+ A 3/2+ A 5+ A 6=12+15-15++0+0=③计算封闭环A 01的极限尺寸:A 01ma x =A 1ma x /2+ A 4ma x /2-A 2min /2+ A 3min /2+ A 5min + A 6min=+-15+=A 01min =A 1min /2+ A 4min /2-A 2ma x /2+ A 3ma x /2- A 5max - A 6ma x=12+-+++=因此,滑块与导轨小端右侧的间隙可写成A 01=38.023.0+- mm,间隙的变动范围为~; ⑵ 滑块与导轨左侧的间隙A 02的计算分析图10-5c 知,A 1/2和A 2/2为增环,A 3/2、A 4/2、A 5和A 6为减环;采用与1同样的步骤建立尺寸链并计算得:封闭环基本尺寸A 02= mm,最大极限尺寸A 02ma x =,最小极限尺寸A 02min =因此,滑块与导轨小端左侧的间隙可写成A 02=51.010.0+- mm,间隙变动范围为~; 当滑块与导轨大端在左侧接触时,滑块与导轨小端左侧和右侧之间的间隙的变动范围与本例计算结果相同; 第三节 用大数互换法计算尺寸链大数互换法是指在绝大多数产品中,装配时各组成环不需挑选或者改变其大小或位置,装入后即能达到封闭环的公差要求,实现一定置信概率下大数互换目的的尺寸链计算方法;该方法采用统计公差公式计算;一、大数互换法的计算公式1.封闭环与组成环公差的关系用数理统计的方法来分析尺寸链时,可以认为各组成环的实际尺寸为独立随机变量,有各种不同的概率分布特征;而封闭环是各组成环的函数,亦为随机变量,也有一定的概率分布特征;实践证明,在大批量生产且稳定的工艺过程中,各组成环实际尺寸的分布接近于正态分布;当各组成环实际尺寸的分布服从正态分布时,封闭环实际尺寸的分布必为正态分布;当各组成环实际尺寸的分布为其它规律的分布时,随组成环环数的增加当环数等于或大于5时,封闭环实际尺寸的分布亦趋向正态分布;采用大数互换法时,可以假设各组成环实际尺寸的分布皆服从正态分布,则封闭环实际尺寸的分布必为正态分布;各组成环实际尺寸分布中心与其公差带中心重合;取置信概率为P =%,则尺寸分布范围与公差带范围相同见图10-6;x —尺寸,φx —概率密度;L —基本尺寸;L ma x 、L min —最大、最小极限尺寸图10-6 上、下偏差ES 、EI 与中间偏差△、公差T 的关系在这种假设下,对于直线尺寸链中封闭环的标准偏差0与各组成环的标准偏差i 的关系如下:σ0=∑=σm 1i 2i 10-7式中 m ——组成环的环数;封闭环公差T 0和各组成环公差T i 分别与各自的标准偏差的关系如下: T 0=6σ0T i =6σi将上两式代入式10-7,则得:T 0=∑=m 1i 2i T 10-8由公式10-8知:尺寸链中封闭环公差等于所有组成环公差的平方之和再开平方;该式称为统计公差公式;2.封闭环与组成环中间偏差的关系参看图10-6,尺寸链中每个尺寸的中间偏差Δ为上偏差ES 与下偏差EI 的平均值,即:=ES +EI /2上、下偏差与中间偏差、公差T 的关系为:ES=Δ+T /2EI=Δ-T /2 10-9对于直线尺寸链,封闭环的中间偏差Δ0与增环中间偏差Δz 、减环中间偏差Δj 的关系式如下:Δ0=∑=l z 1Δz -m l j +=∑1Δj 10-10 二、设计计算大数互换法设计计算步骤与完全互换法大致相同;首先,假设各组成环的公差相等,即T 1= T 2=…=T m = T av,Q T av,Q 为各组成环平均公差;由式10-8得:T 0=2Q ,av mT因此,各组成环的平均公差 用下式计算:T Q .aV =T 0/m 10-11然后,在此基础上调整各组成环的公差,并确定各组成环极限偏差;例4 用大数互换法求解例1;假设例1中各组成环实际尺寸的分布皆服从正态分布,各组成环实际尺寸分布中心分别与各自公差带中心重合,且实际尺寸分布范围与公差带范围重合;解:封闭环A 0=035.010.0++ mm,封闭环公差T 0=;按式10-11计算各组成环公差的平均公差:T av,Q =T 0/m =5=然后,在满足10-8的条件下,按各组成环的尺寸大小和加工难易程度,调整他们的公差,得:T 1= T 3 = ,T 2 = T 5 = ,T 4= 标准件,A 4=3005.0 - mm最后,确定各组成环的极限偏差;先按“偏差入体”原则,确定组成环A 1、A 2、A 5和A 4的极限偏差,这四个组成环的基本尺寸和极限偏差分别为:A 1=30016.0 -mm,A 2=A 5=5006.0 -mm,A 4=3005.0 -mm;由封闭环和上述四个组成环的极限偏差分别计算它们的中间偏差,得:0=+,1=,2=5=,4= 由式10-10计算剩下一个组成环A 3的中间偏差,得:3=0+1+2+4+5=再由式10-9计算组成环A 3的极限偏差,得:ES 3 = 3 + T 3/2 = + 2 = +EI 3 = 3 - T 3/2 = - 2 = -因此,组成环A 3的极限偏差为:A 3=4314.002.0+- mm比较本例与例1,在封闭环公差一定的条件下,T av,Q /T av,L ==倍,这对加工是有利的,但可能有%的产品装配时超差;三、校核计算校核计算用式10-1、式10-8、式10-10和式10-9进行;例5 用大数互换法求解例3;假设,本例中各组成环实际尺寸的分布皆服从正态,且分布中心与公差带中心重合,分布范围与公差带范围相同;解:⑴ 滑块与导轨小端右侧的间隙A 01的计算参看图10-5b 及例3,已知组成环中A 1/2=120.140+ mm 和A 4/2=1502.004.0-- mm 为增环,A 2/2=150.07 +0 mm 、 A 3/2=014.0 - mm 、A 5=0和A 6=0为减环;① 计算封闭环A 01的中间偏差1/2=+、2/2=+、3/2=、4/2=、5=0、6=0,因此由式10-10计算封闭环中间偏差得: Δ01=Δ1/2+ Δ4/2-Δ2/2+ Δ3/2+ Δ5+ Δ6= =② 计算封闭环公差由式10-8计算封闭环公差,得:T 01=∑=m i i 12T =262524232221)2()2()2()2(T T T T T T +++++=22222210.014.002.014.007.014.0+++++=③ 计算封闭环的上、下偏差由式10-9计算封闭环的上、下偏差,得:ES 01 = 01 + T 01/2 = + 2 = +EI 01 = 01 – T 01/2 = - 2 = -因此,封闭环A 01=21.007.0+-,它的最大、最小极限尺寸分别为:A 01max = ES 01+ A 01 = + = mmA 01min = EI 01 + A 01= + =即:滑块与导轨小端右侧的间隙变动范围为~ mm;⑵ 滑块与导轨左侧的间隙A 02 的计算参看图10-5c ,用同样的方法计算得A 02=34.007.0++ mm;因此,滑块与导轨小端左侧的间隙变动范围为~ mm;与例3用完全互换法计算相比较,用大数互换法计算易于达到封闭环的公差要求; 习 题10—1 什么叫尺寸链如何确定封闭环、增环和减环10—2 计算尺寸链的目的是什么10—3 计算尺寸链的常用方法有哪几种,它们分别用在什么场合10—4 为什么封闭环的公差比任何一个组成环公差大10—5 什么是尺寸链最短原则说明此原则的重要性;10—6 加工习题10—6附图所示的套筒时,外圆柱面加工至A 1=ф80F9, 内孔加工至A 2=ф60H8,外圆柱面轴线对内孔轴线的同轴度公差为ф;试计算套筒壁厚尺寸的变动范围;习题10—6附图10—7 参看习题10—7附图所示的链传动机构,要求装配后链轮左端面与右侧轴承右端面之间保持~的间隙;试用完全互换法和大数互换法分别计算影响该间隙的有关尺寸的极限偏差;习题10—7附图10—8 参看习题10—8附图,孔、轴间隙配合要求ф50H9/f9,而孔镀铬使用,镀层厚度C2=C3=10μm 2μm,试计算孔镀铬前的加工尺寸;习题10—8附图。