下载文档原格式
关于静电场唯一性定理的讨论
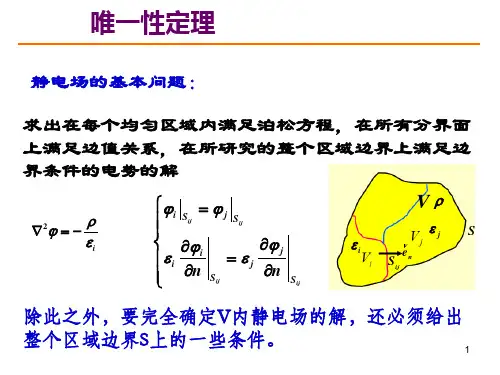
静电场唯一性定理是物理中一个重要的理论，说明了每个静电场系
统有唯一的电场强度，且不会改变。
这个定理的本质就是给电场的描
述赋予了确定性，因而被称为“唯一性”。
它宣称，一个静电场系统里
有唯一的电势差和电势强度，并且这个数值的变化应该是可以计算的，而不会由于外部因素造成变化。
由于静电场唯一性定理的实用性，它被广泛应用在电动学问题中，有
助于计算电力和其他重要物理量。
因此，它也被认为是物理学中最基
本的定律之一。
此外，它还可以用来解释为什么只有恒定的电压供应，而不会因外界因素而变化。
唯 性定 唯一性定理汪 毅静电问题的唯一性定理均匀分区的区域V，即V可以分为若干个均匀区域Vi， 每个均匀区域的电容率为ε 设 内有给定的自由 每个均匀区域的电容率为 i，设V内有给定的自由 电荷分布ρ(x)。
电势ϕ在均匀区域Vi内满足泊松方 ρ ϕ 程：ρ ∇ ϕ =− εi2在两区域Vi和Vj的分界面上满足边值关系：ϕi = ϕ j∂ϕ j ∂ϕi εi =εj ∂n ∂n静电问题的唯一性定理要完全确定V内电场，还必须给出V的边界S上的一 些条件。
下面提出的唯 性定理具体指出所需给定 些条件。
下面提出的唯一性定理具体指出所需给定 的边值条件： 1）给定边界S的电势 2）给定边界S的电势法向偏导数 或者说V内存在唯一的解，它在每个均匀区域内满 足泊松方程，在两均匀区域分界面上满足边值关系， 并在 的边界上满足给定的ϕ或者∂ϕ/∂ 并在V的边界上满足给定的ϕ或者∂ϕ/∂n唯 性定理证明 唯一性定理证明 证明：假定泊松方程有两个解 ϕ1 , ϕ 2 ，满足：在边界上：ρ ∇ ϕ1 = ε2ρ ∇ ϕ2 = ε2ϕ1 S = ϕ 2令：S=ϕ S∂ϕ1 ∂nS∂ϕ ∂ϕ2 = = ∂n S ∂nSΦ = ϕ1 − ϕ2 ∇2Φ =∇2ϕ1 −∇2ϕ2 = 0 ∇ ∇唯一性定理证明Φ S = ϕ1 S − ϕ2 S∂ϕ2 ∂ϕ1 ∂Φ − =0 = ∂n S ∂n ∂n S =0S考虑第i个均匀区域Vi的界面Si上的积分∫Siε i Φ ∇Φ ⋅ dS∫根据格林第一公式： 根据格林第 公式Si ViεiΦ ∇Φ⋅ dS = ∫ ∇ (εiΦ ∇Φ )dV ∇Φ ∇⋅= ∫ εi (∇Φ ) dV + ∫ ϕεi∇ Φ dV2 2 Vi Vi唯一性定理证明 2 ε i Φ ∇Φ ⋅ dS = ∫ ε i (∇Φ ) dV ∫S Vi i对所有分 域 求 对所有分区域Vi求和∑∫iSiε i Φ ∇Φ ⋅ dS = ∑ ∫ ε i (∇Φ ) dV2 i ViΦ 在两均匀区域Vi和Vj界面上， 和ε ∇Φ 的法向分 量分别相等，但 dSi = − dS j ，因此上式左边的和 式中，内部分界面的积分互相抵消，因此只剩下整 式中 内部分界面的积分互相抵消 因此只剩下整 Φ 个V的边界面S上的积分。
静电场电位边值问题唯一性定理的补充与完整证明陈文卿;闫述【摘要】The electrostatic boundary value problem and the uniqueness of solutions are sup-plemented and proved in this paper.At first,the region condition and the convergence bound-ary are distinguished from the usual mixed singularity.The form of Robin Problem in electro-static field boundary value problem is confirmed.The convergence condition and the infinite boundary condition are added to the uniqueness theorem of solutions.These boundary condi-tions are re-classified according to the form of mathematical expressions.Then in the proof of the uniqueness of the potential solutions under boundary conditions,infinite boundary condi-tions and convergence conditions,the problem of the coefficient of the third kind of boundary condition and the applicative boundary value problem with infinite space are solved.We also demonstrate the uniqueness of potential solutions for Dirichlet and Robin Problem and con-stant differences in the potential of Neumann Problem.Finally,the application of region,in-finity and convergence boundary conditions in problems solving is illustrated by an example.The supplemented theorem can be better used as the basis for solving problems and follow-up learning.%本文对静电场电位边值问题与解的唯一性定理作了补充与完整的证明.首先将区域边界与衔接边界从通常的混称中区分开来,确认了静电场边值问题中第三类边界条件应有的形式,在解的唯一性定理中增加了衔接条件和无限远边界条件,并根据数学表达式的形式重新归类.然后在区域边界条件、无限远边界条件和衔接条件下电位解的唯一性的证明中,讨论了第一、第三类边值问题电位解的唯一性与全二类边界条件下电位存在常数差的问题,解除了第三类边界条件系数为正的限制,说明了整个求解空间为无限大时适用的边值问题.最后通过例题说明了区域、无限远和衔接3种边界条件在解题中的应用.补充后的定理可以更好地作为解题和后续学习的依据和基础.【期刊名称】《物理与工程》【年(卷),期】2017(027)006【总页数】6页(P54-59)【关键词】电位的边值问题;区域边界条件;衔接条件;唯一性定理;证明【作者】陈文卿;闫述【作者单位】江苏大学计算机科学与通信工程学院,江苏镇江 212013;江苏大学计算机科学与通信工程学院,江苏镇江 212013【正文语种】中文电位的边值问题与解的唯一性是通信和电子信息类相关专业本科阶段电磁场与电磁波和电动力学课程中静电场部分的重要内容，也是求解其他边值问题的基础。
